Журнал неорганической химии, 2019, T. 64, № 4, стр. 389-396

Описание донорно-акцепторной связи с помощью теории обобщенных зарядов

А. М. Долгоносов^1, *

¹ Институт геохимии и аналитической химии им. В.И. Вернадского РАН
119991 Москва, ул. Косыгина, 19, Россия

Поступила в редакцию 01.10.2018
После доработки 04.10.2018
Принята к публикации 16.10.2018

DOI: 10.1134/S0044457X19040093

Аннотация

С помощью теории обобщенных зарядов, представляющей собой асимптотическое приближение для межатомных сил квантово-статистической модели многокомпонентного электронного газа, ранее было получено универсальное соотношение для энергии и длины гомополярной ковалентной связи. В статье рассмотрены новые следствия теории, полученные для описания донорно-акцепторной связи. Энергия связи включает в себя вклад атома-донора, характерный для гомополярной связи, и кулоновское взаимодействие атомов с учетом вероятности фиксации электронов связи на акцепторе. Найдены закономерности для длины и энергии донорно-акцепторной связи, в том числе для частного случая, реализующегося у гидридов, получены выражения для длины и энергии связи через атомный номер акцептора.

Ключевые слова: химическая связь, ковалентное взаимодействие, энергия и длина химической связи, обобщенный заряд

ВВЕДЕНИЕ

Главной проблемой, мешающей достижению приемлемой точности при описании межатомных взаимодействий (МАВ) с помощью неэмпирических методов, является разный масштаб энергий, входящих в единую сумму для энергии молекулы: для взаимодействия электронов между собой и с ядром внутри атома (10¹–10² эВ), с одной стороны, между атомами – с другой (10⁰ эВ), и между молекулами – с третьей (10^–2–10^–1 эВ). При тех упрощениях гамильтониана и волновой функции, которые используются в методе Хартри–Фока [1, 2], или потенциала в теории функционала плотности (ТФП) [3, 4] их точность остается недостаточной. Приближение Хартри–Фока не учитывает кулоновскую корреляцию электронов, которая, согласно ТФП, характеризуется энергией, сопоставимой по масштабу с МАВ. Кроме того, на точность (и возможность) расчета влияет выбор исходного базиса волновых функций, разного в разных случаях. В свою очередь, использование ТФП сильно зависит от базисного набора функций для электронной плотности (которые в ряде случаев носят эмпирический характер), что сильно снижает ценность метода для предсказания МАВ неизвестных систем.

Выходом из такой ситуации является разработка асимптотического описания поля атомных электронов, более слабого вне атомов. Как показывает химический опыт, сконцентрированный в виде Периодической таблицы элементов, внеатомное поле, определяющее химические свойства атомов, связано с зарядом ядра только параметрически, и его можно представить уравнениями для собственных потенциалов без включения потенциалов внутриатомного поля. Иллюстрацией этой мысли служит простое эмпирическое правило сложения атомных радиусов при оценке длины химической связи между атомами. Однако это правило, ввиду своей грубости, вносит путаницу в понятие размера атома и приводит к серьезным ошибкам.

В развитие метода Томаса–Ферми [4], являющегося базой для ТФП, в наших работах [5–8] была предложена модель многокомпонентного электронного газа, позволяющая с достаточной точностью описать поле атомных электронов в границах атома. Следствием развитых представлений для асимптотической области вдали от ядра явилась теория обобщенных зарядов (ТОЗ) [8–11]. Термин “обобщенный заряд” своим происхождением обязан двум обстоятельствам: во-первых, заряд вводится формально – как величина, пропорциональная энергии межатомного взаимодействия, т.е. как обобщенная характеристика фундаментальных свойств молекулы или ее части; во-вторых, являясь по своей природе производным электростатических сил, обобщенный заряд объединяет участие в межатомном поле одновременно нескольких электронов, обобщенных в этом смысле в рамках молекулы или молекулярного фрагмента. Формально обобщенные заряды можно свести к атом-атомным потенциалам. Однако в отличие от полуэмпирических методов, разработанных для описания межатомных и межмолекулярных взаимодействий, опирающихся на ошибочный постулат об аддитивности атом-атомных потенциалов [12, 13], в ТОЗ выводится новое правило сумм, благодаря которому достигается приемлемая точность описания явлений без использования подгоночных параметров. В частности, ТОЗ демонстрирует хорошие возможности в априорном расчете ван-дер-ваальсовых взаимодействий, адсорбции, поверхностного натяжения [8–11, 14] при описании ковалентной связи [15–17]. В отличие от упомянутых полуэмпирических подходов, ТОЗ обоснованно, без подгоночных процедур определяет параметры взаимодействий через электронную структуру связываемых молекулярных фрагментов и часто доводит уровень описания до соответствия структура–свойство.

В статье [17] на базе ТОЗ дан вывод уравнения для энергии и длины ковалентной связи и проанализированы характеристики двухатомных молекул в основном состоянии. Полученное уравнение имеет отношение, строго говоря, только к гомополярным соединениям. В предлагаемой работе указанное описание используется для вывода на базе ТОЗ выражений для донорно-акцепторной связи и ее частного случая – связи в гидридах.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Обобщенный заряд

Теория обобщенных зарядов использует понятие “жесткий фрагмент” (структура, объединяющая атомы по принципу обобществления их электронов) и его количественную характеристику – “обобщенный заряд” – коэффициент пропорциональности между энергией и потенциалом поля межатомных взаимодействий:

(1)

$U\left( r \right) = QQ{\text{'}}{{u}_{b}}\left( r \right),$

где $Q,\,\,Q{\text{'}}$ – обобщенные заряды двух молекулярных фрагментов, ${{u}_{b}}\left( r \right)$ – функция расстояния между ними.

В ТОЗ выводится закон сложения:

(2)

${{Q}^{b}} = \sum\limits_i {Q_{i}^{b}} ,$

где $Q$ – обобщенный заряд жесткого фрагмента, объединяющего атомы с обобщенными зарядами ${{Q}_{i}},$ $b$ – параметр модели многокомпонентного электронного газа (например, $b = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$ – для компоненты газа Томаса–Ферми, ответственной за ковалентную связь, $b = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}$ – для компоненты электронного газа, участвующей в ван-дер-ваальсовом притяжении [6–8]). Если представить правило (2) двумя соотношениями:

(3)

$Q = {{V}^{{{1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}}}},\,\,\,\,V = \sum\limits_i {{{V}_{i}}} ,$

то возникает в явном виде аддитивная величина $V$ – “электронный объем”. Электронный объем – это не просто сумма чисел валентных электронов: вклад каждого электрона связан с кратностью вырождения его состояния, как корень квадратный из этого числа – обычно 1 и $\sqrt 2 $ [15, 16].

Число электронов жесткого фрагмента $N = \sum\nolimits_i {{{N}_{i}}} ,$ находящихся в области его взаимодействия с другими фрагментами, ограничено эффектом экранирования [18]. Для каждого атомного электрона эффект характеризуется сферой экранирования, из которой его выход без изменения состояния (возбуждения) запрещен. Выражение для радиуса экранирования ${{r}_{s}}$ электронов ковалентной связи выводится из предположения о сферической симметрии элементарной ячейки фазового пространства электронов связи [17]:

(4)

${{r}_{s}} = \frac{{1.710e\sqrt {{{a}_{0}}z} }}{{\sqrt {{{E}_{0}}} }},$

где $1.710 = {{\left( {{{81{{\pi }^{2}}} \mathord{\left/ {\vphantom {{81{{\pi }^{2}}} {32}}} \right. \kern-0em} {32}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}},$ $e$ – элементарный заряд, ${{a}_{0}} = \frac{{{{\hbar }^{2}}}}{{m{{e}^{2}}}}$ – радиус Бора, m – масса электрона, z – число электронов связи, ${{E}_{0}}$ – модуль потенциальной энергии связи. Область экранирования ограничена огибающей поверхностью сфер экранирования электронов фрагмента.

Энергия межатомного взаимодействия

Поскольку энергия взаимодействия пропорциональна обобщенному заряду, а аддитивной является величина V, энергия связи жесткой молекулы не является суммой энергий частей молекулы, как это часто полагают в полуэмпирических подходах. Из (3) следует, что в жесткой молекуле аддитивной является энергия (потенциал), возведенная в степень b.

В согласии с этим выводом находятся полученные в работе [9] выражения для ковалентного и ван-дер-ваальсового взаимодействий. Возможности последнего при описании адсорбции показаны, например, в работах [8, 10, 11]. Потенциальная энергия ковалентной связи имеет вид:

(5)

$\begin{gathered} {{U}_{{\operatorname{cov} }}} = \frac{{5 - 2\sqrt 2 }}{3}\left( {{{V}_{m}}{{V}_{{m'}}}} \right)\frac{{{{e}^{2}}}}{{{{r}_{{mm'}}}}}\exp \left( { - \frac{{2\sqrt 5 {{r}_{{mm'}}}}}{{{{a}_{0}}}}} \right) - \\ - \,\,\frac{{8 - 4\sqrt 2 }}{3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left( {VV'} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\frac{{{{e}^{2}}a_{0}^{3}}}{{{{r}^{4}}}}, \\ \end{gathered} $

где ${{V}_{m}},$ ${{V}_{{m'}}},$ ${{r}_{{mm'}}}$ – электронные объемы ближайших атомов фрагментов и расстояние между ними соответственно; $V,\,\,V{\text{'}}$ – электронные объемы жестких молекулярных фрагментов, между которыми рассматривается взаимодействие, $r$ – расстояние между ними. В случае двухатомной молекулы, рассмотренной ниже: ${{V}_{m}} = V,$ ${{V}_{{m'}}} = V',$ ${{r}_{{mm'}}} = r$ – параметры атомов.

Для равновесных расстояний положительный член в (5) гораздо меньше отрицательного (например, для атомов в молекуле водорода первый член равен ~2 кДж/моль – по сравнению со вторым ~–440 кДж/моль), и поэтому в дальнейшем для упрощения выкладок мы им пренебрежем. Потенциальная энергия (5) выводится для синглетной компоненты электронного газа, ячейка которой содержит два электрона связи. Если число связывающих электронов z, то энергия такой системы будет в ${z \mathord{\left/ {\vphantom {z 2}} \right. \kern-0em} 2}$ раз больше: ${{z{{U}_{{\operatorname{cov} }}}} \mathord{\left/ {\vphantom {{z{{U}_{{\operatorname{cov} }}}} 2}} \right. \kern-0em} 2}.$ Таким образом, модуль потенциальной энергии ковалентной связи в точке равновесия (индекс “e”) равен:

(6)

${{E}_{0}} = - \frac{z}{2}{{U}_{{\operatorname{cov} e}}} \approx 0.3905z{\kern 1pt} {{\left( {VV{\text{'}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\frac{{{{e}^{2}}a_{0}^{3}}}{{r_{e}^{4}}}.$

Энергия диссоциации двухатомной молекулы отличается от модуля потенциальной энергии связи на вращательный и колебательный члены, однако при нулевой температуре и в рассматриваемом случае основного состояния энергией колебаний можно пренебречь, а вращательную энергию учитывать только у электронов (для намного более массивных ядер значение второго члена в (7), в знаменателе которого стоит масса, мало):

(7)

${{E}_{\lambda }} \approx {{E}_{0}} - \frac{{{{\hbar }^{2}}\lambda }}{{mr_{e}^{2}}},$

где $\lambda = \sum {{{l\left( {l + 1} \right)} \mathord{\left/ {\vphantom {{l\left( {l + 1} \right)} 2}} \right. \kern-0em} 2}} $ – полуквадрат момента электронов связи в атомных единицах (ПКМ), $l$ – момент в атомных единицах (молекулярное орбитальное число).

Функция связи

Энергия ковалентной связи является функционалом избыточной электронной плотности в межъядерном пространстве. Избыточная величина получается как разность между реальной электронной плотностью и суммой плотностей в той же точке, взятых для гипотетического случая изолированных атомов. Она пропорциональна общему числу электронов в атомах и вероятности их участия в ковалентном взаимодействии, которая приблизительно равна $\int_r {{{{\left| \psi \right|}}^{2}}dx} - \frac{1}{2}$ – разности между вероятностью для электрона оказаться между атомами (межъядерное расстояние r) и ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ – значением вероятности для него быть в этом полупространстве при рассмотрении изолированного атома. Указанное выражение является асимптотическим при $r \to \infty ,$ которое, благодаря очень быстрому снижению электронной плотности с удалением от ядра, достаточно точно выполняется уже для расстояний порядка длин ковалентных связей. С другой стороны, электроны, участвующие в связи атомов, принадлежат пересечению их электронных объемов ${{V}_{1}} \cap {{V}_{2}}.$ Имеет место уравнение [8, 15]:

(8)

$\sqrt {{{V}_{1}}{{V}_{2}}} = \left( {{{Z}_{1}} + {{Z}_{2}}} \right){\kern 1pt} {\kern 1pt} \left( {\int\limits_r {{{{\left| \psi \right|}}^{2}}dx} - \frac{1}{2}} \right),$

где ${{Z}_{1}},$ ${{Z}_{2}}$ – атомные номера; $\psi \,\left( x \right)$ – электронная волновая функция; интегрирование проводится по межатомному отрезку r. Электронный объем является частью множества электронов атома, $\left\{ V \right\} \subset \left\{ Z \right\}$ и пересечение электронных объемов есть пересечение множеств атомных электронов, т.е. вместо произведения электронных объемов в левой части формулы (8) можно подставить произведение атомных номеров, умноженное на функцию от межатомного расстояния. Так вводится “функция связи”:

(9)

$\alpha \left( r \right) = \sqrt {\frac{{{{V}_{1}}{{V}_{2}}}}{{{{Z}_{1}}{{Z}_{2}}}}} .$

Функция связи имеет смысл вероятности электронного обмена между атомами. В работе [16] показано, что эта функция хорошо описывается как косинус полусуммы фаз электронов межатомной связи:

(10)

$\alpha \left( r \right) \approx \cos \beta r,\,\,\,\,\beta = \frac{1}{2}\sum\limits_z {{{k}_{i}}} ,$

где ${{k}_{i}}$ – проекция волнового вектора электрона на ось связи.

Заметим, что электроны ($\pi ,\delta ,...$) с ненулевой проекцией момента на ось имеют нулевую проекцию волнового вектора и не дают вклада в коэффициент $\beta .$ Этот факт был использован при определении отношений длин связей различной кратности [16].

Из условия неучастия экранированных электронов в образовании связи, $\alpha \left( {{{r}_{s}}} \right) \equiv 0,$ коэффициент $\beta $ выражается через радиус экранирования:

(11)

$\beta = \frac{\pi }{{2{{r}_{s}}}}.$

Отметим, что формула (11) определяет единое значение радиуса экранирования для электронов связываемых атомов. Факторизация в согласии с (9) выражения (10) даст для коротких связей (${{r}_{e}} \ll {{r}_{s}}$) так называемые “атомные функции связи”:

(12)

$\sqrt {\frac{{{{V}_{i}}}}{{{{Z}_{i}}}}} = \cos \frac{{\pi {{r}_{i}}}}{{2{{r}_{s}}}},\,\,\,\,i = 1,2,$

где ${{r}_{i}}$ – атомные радиусы (${{r}_{1}} + {{r}_{2}} \approx {{r}_{e}}$).

Уравнение для энергии и длины ковалентной связи

В работе [17] из выражений для потенциальной энергии (6), функции связи (9)–(11) и радиуса экранирования (4) было получено уравнение:

(13)

$x = \frac{{0.8838}}{{\sqrt y }}{{\cos }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\left( {0.6496\sqrt y } \right),$

($0.6496 = {{\left( {{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},$ $0.8838 = \sqrt {0.7810} $) для безразмерных параметров длины (x) и энергии (y) связи:

(14)

$x = \frac{{{{r}_{e}}}}{{{{a}_{0}}{{{\left( {{{Z}_{1}}{{Z}_{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}},$

(15)

$y = \frac{{2{{E}_{0}}r_{e}^{2}}}{{z{{a}_{0}}{{e}^{2}}}} = \frac{2}{z}\left( {\frac{{{{E}_{\lambda }}r_{e}^{2}}}{{{{a}_{0}}{{e}^{2}}}} + \lambda } \right).$

Параметрами зависимости энергии диссоциации двухатомной молекулы от ее размера служат число и ПКМ электронов связи (z и $\lambda $). Число электронов связи соответствует ее кратности (для простой связи 2 электрона и т.д.).

Способ определения ПКМ связи базируется на анализе электронного строения связываемых атомов. Цилиндрическая симметрия двухатомных молекул обусловливает сохранение только проекции момента на ось молекулы, т.е. магнитного числа m, но не орбитального, для сохранения которого нужна центральная симметрия. Однако орбитальное число основного состояния двухатомных молекул можно найти косвенным способом, учитывая следующие условия: орбитальное число для основного состояния является минимальным из возможных, момент не меньше своей проекции по модулю ($l \geqslant \left| {\mathbf{m}} \right|$), – таким образом, орбитальное число равно максимальному из магнитных чисел $l = {{\left| {\mathbf{m}} \right|}_{{max}}},$ реализующихся в этом состоянии.

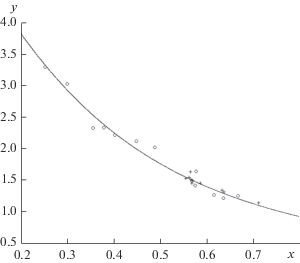
Уравнение (13) описывает универсальную закономерность для гомополярных связей, выведенную теоретически и проиллюстрированную данными по двухатомным молекулам в статье [17] (рис. 1). Для определения каждой из переменных уравнения (13) требуются дополнительные сведения о характере связи. Ниже в этом ключе рассмотрена разновидность полярного МАВ–донорно-акцепторная связь.

Рис. 1.

Иллюстрация зависимости (13) для гомополярных молекул (сплошная линия). Обозначены экспериментальные точки: (o) – молекулы с простыми связями (CCl, CBr, ClF, BrF, Cl₂, Br₂, JF, BrJ, J₂, Au₂, Hg₂); (+) – молекулы с кратными связями (C₂, CN, CO, N₂, NO, O₂, CS, PO, SO, S₂).

Донорно-акцепторная связь

Энергия донорно-акцепторной связи. Факт “посещения” атомной орбитали атома-акцептора (a‑атома) электроном атома-донора (d-атома) в случае донорно-акцепторных (da-) связей соответствует взаимной ортогональности волновых функций электронов связи, что соответствует их невырожденным состояниям. В результате взаимодействия возникает состояние, в котором c электронов d-атома локализованы в оболочке a‑атома. В этом состоянии атомы приобретают противоположные заряды величиной $ce.$ Энергия da-связи является суммой вкладов каждого из атомов и кулоновской энергии зарядов за вычетом орбитального члена:

(16)

${{E}_{{da}}} = {{E}_{d}} + {{E}_{a}} + \frac{{a{{c}^{2}}{{e}^{2}}}}{{{{r}_{e}}}} - \frac{{{{\hbar }^{2}}\lambda }}{{mr_{e}^{2}}}.$

Электроны d-атома, участвующие в связи, выходят в межатомное пространство, поэтому их энергия подчиняется выражению (6), записанному для одного из атомов, как если бы связь была гомополярной:

(17)

${{E}_{d}} = \frac{1}{2}{{E}_{0}} \approx 0.3905c{{\left( {{{Z}_{d}}{{Z}_{a}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\frac{{{{e}^{2}}a_{0}^{3}}}{{r_{e}^{4}}},$

где использованы формула (9) и соотношение $z = 2c,$ отражающее равенство чисел электронов связи от каждого атома.

Энергия a-атома тратится на захват электронов, поэтому можно предположить, что вклад a-атома в энергию связи намного меньше вклада других членов, и мы им в наших оценках пренебрежем (${{E}_{a}} \approx 0$).

Кулоновское взаимодействие возникает в те моменты, когда электроны атома-донора локализованы на a-атоме. Поскольку вероятность для атомного электрона может быть в межатомном пространстве равна функции связи $\alpha ,$ его фиксация на акцепторе происходит с вероятностью $a = 1 - \alpha .$

Таким образом:

(18)

$\begin{gathered} {{E}_{{da}}} \approx 0.3905{{\left( {{{Z}_{d}}{{Z}_{a}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{\alpha }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\frac{{c{{e}^{2}}a_{0}^{3}}}{{r_{e}^{4}}} + \\ + \,\,\left( {1 - \alpha } \right)\frac{{{{c}^{2}}{{e}^{2}}}}{{{{r}_{e}}}} - \frac{{{{\hbar }^{2}}\lambda }}{{mr_{e}^{2}}}. \\ \end{gathered} $

Как правило, в da-связях перемещаемые электроны d-атома находятся в s-состоянии с нулевой проекцией момента в частности, это имеет место в рассмотренных ниже примерах, значение ПКМ будем полагать нулевым.

Функция донорно-акцепторной связи. Когда к a-атому добавляется электрон, он становится отрицательным ионом. Такой ион можно представить как атом с характеристиками ${{Z}_{a}} + 1$ и ${{V}_{a}} + 1$ и функцией связи $\sqrt {\frac{{{{V}_{a}} + 1}}{{{{Z}_{a}} + 1}}} .$ Однако у положительного иона с электронным строением инертного газа функция связи равна не $\sqrt {\frac{{{{V}_{d}} - 1}}{{{{Z}_{d}} - 1}}} ,$ а ~1. Дело в том, что оболочка инертного газа у положительного иона очень плотно сконцентрирована вокруг ядра и его размер ${{r}_{ + }}$ настолько мал, что величина (12): $\cos \left( {{{\pi {{r}_{ + }}} \mathord{\left/ {\vphantom {{\pi {{r}_{ + }}} {2{{r}_{s}}}}} \right. \kern-0em} {2{{r}_{s}}}}} \right) \approx 1.$ У протона эта величина с высокой точностью равна 1, у катионов щелочных металлов она имеет порядок 0.95. Аналогично и с многозарядными катионами (случай $c > 1$).

Таким образом, функция связи, при которой c электронов d-атома перемещаются в оболочку a-атома, задается формулой:

(19)

${{\alpha }_{{da}}} \approx \sqrt {\frac{{{{V}_{a}} + c}}{{{{Z}_{a}} + c}}} .$

В отличие от (9) выражение (19) означает, что атомы da-связи не независимы: атом-донор, отдав валентные электроны, не участвует другими электронами в межатомном взаимодействии, а атом-акцептор, приняв эти c электронов d-атома, обладает увеличенным на c числом электронов.

Длина донорно-акцепторной связи. Радиус экранирования определяет область распространения электронной плотности атомов, участвующих в связи, и соответствует энергии высшего заполненного уровня. В рассматриваемой системе самый высокий уровень занимает электрон атома-донора. Его энергия выше (т.е. меньше по абсолютной величине) средней энергии электронов связи, использованной в выражении (4). Этим выражение (4) для радиуса экранирования в случае da-связи отличается от случая гомополярной связи, что приводит к погрешности в формулах (13), (14). Эту трудность можно обойти.

Запишем выражения (10), (11) в виде

(20)

${{r}_{s}} = \frac{\pi }{{2{{\beta }_{{da}}}}} = \frac{{\pi {{r}_{e}}}}{{2\arccos {{\alpha }_{{da}}}}}.$

Из сказанного выше следует, что ${{\beta }_{{da}}} \to {{\beta }_{d}},$ и для равновесного расстояния имеет место уравнение:

(21)

${{r}_{e}} \equiv {{r}_{{da}}} = \beta _{d}^{{ - 1}}\arccos {{\alpha }_{{da}}}.$

Величина ${{\beta }_{d}}$ определяется из условия (4) для гомополярной связи:

(22)

${{\beta }_{d}} = \frac{{0.9185}}{{e\sqrt {{{a}_{0}}z} }}\sqrt {{{E}_{{dd}}}} ,$

где ${{E}_{{dd}}}$ – модуль потенциальной энергии в гомоядерной молекуле, состоящей из d-атомов, z является числом электронов указанной связи.

В том случае, когда ковалентное гомоядерное соединение dd отсутствует, можно воспользоваться приближенным соотношением:

(23)

${{\beta }_{d}} \approx \frac{{0.6495}}{{e\sqrt {{{a}_{0}}c} }}\sqrt {{{E}_{{da}}}} ,$

где сделаны замены $z \to 2c$ и ${{E}_{{dd}}} \to {{E}_{{da}}}.$

Итак, согласно (21)–(23), длина донорно-акцепторной связи равна:

(24)

$\begin{gathered} {{r}_{{da}}} = \frac{{1.0886e\sqrt {{{a}_{0}}z} }}{{\sqrt {{{E}_{{dd}}}} }}\arccos \sqrt {\frac{{{{V}_{a}} + c}}{{{{Z}_{a}} + c}}} \approx \\ \approx \frac{{1.550e\sqrt {{{a}_{0}}c} }}{{\sqrt {{{E}_{{da}}}} }}\arccos \sqrt {\frac{{{{V}_{a}} + c}}{{{{Z}_{a}} + c}}} . \\ \end{gathered} $

Например, длина связи молекулы BeO ($c = 2,$ ${{V}_{a}} = 6,$ ${{Z}_{a}} = 8,$ ${{E}_{{da}}} = 430$ кДж/моль) по формуле (24) равна 0.131 нм (экспериментальное значение 0.133 нм [19]).

Для электронного объема акцептора можно принять соотношение:

(25)

${{V}_{a}} = {{Z}_{a}} - 2{{\left( {{{n}_{a}} - 1} \right)}^{2}} + \sqrt 2 \left( {{{n}_{a}} - 2} \right),$

где ${{n}_{a}}$ – номер периода акцептора. Формула (25) имеет следующий смысл: разность между атомным номером и электронным объемом равна полному набору состояний внутренней оболочки атома $2{{\left( {n - 1} \right)}^{2}}$, за исключением состояний, имеющих ненулевую проекцию момента на ось связи, числом $n - 2$ с весом $\sqrt 2 ,$ так как они дважды вырождены по знаку проекции момента.

Переходя к безразмерной переменной (15), из (24), (25) получим:

(26)

$y \approx 2.402{{\arcsin }^{2}}\sqrt {\frac{{2{{{\left( {{{n}_{a}} - 1} \right)}}^{2}} - \sqrt 2 \left( {{{n}_{a}} - 2} \right)}}{{{{Z}_{a}} + c}}} .$

Часто выполняется так называемое в химии правило октетов – равенство ${{Z}_{a}} + c = {{Z}_{n}},$ где ${{Z}_{n}}$ – атомный номер ближайшего к акцептору инертного газа. Тогда получим:

(27)

${{y}_{n}} = 2.402{{\arcsin }^{2}}\sqrt {\frac{{2{{{\left( {n - 1} \right)}}^{2}} - \sqrt 2 \left( {n - 2} \right)}}{{{{Z}_{n}}}}} $

набор констант для 2–6-го периодов соответственно: 0.516, 1.014, 1.199, 1.535, 1.541. Ввиду грубости полученного соотношения из-за приближения (23) этот вывод можно считать лишь ориентиром для da-соединений.

Гидриды как частный случай донорно-акцепторной связи

У молекулы гидрида HX обычно донором является атом водорода. Характеристики молекулы водорода: $z = 2$ и ${{E}_{{dd}}} = {{E}_{{{{{\text{H}}}_{{\text{2}}}}}}} \approx $ 437.5 кДж/моль. Численный коэффициент в (24) в таком случае равен $1.710 \times 4\sqrt 3 {\text{/}}\pi = 3.771.$

Гидриды элементов 2-го периода

Сначала рассмотрим более понятный пример с гидридами атомов 2-го периода, для которых электронный объем равен числу электронов внешней оболочки атома ${{V}_{a}} = {{Z}_{a}} - 2$ (в согласии с (25)) и $c = 1.$ На основании (24) запишем формулу (далее индекс “a” опускаем):

(28)

$\begin{gathered} {{r}_{{{\text{HX}}}}} = 3.771{{a}_{0}}\arccos \sqrt {\frac{{V + 1}}{{Z + 1}}} = \hfill \\ = \,\,3.771{{a}_{0}}\arcsin \sqrt {\frac{2}{{Z + 1}}} . \hfill \\ \end{gathered} $

Формула (18) для энергии связи гидридов атомов 2-го периода примет вид:

(29)

$\begin{gathered} {{E}_{{{\text{HX}}}}} \approx \,\frac{{1.931 \times {{{10}}^{{ - 3}}}{{e}^{2}}}}{{{{a}_{0}}\arcsin \sqrt {{2 \mathord{\left/ {\vphantom {2 {\left( {Z + 1} \right)}}} \right. \kern-0em} {\left( {Z + 1} \right)}}} }}{\kern 1pt} \left[ {{{Z}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{{\left( {\frac{{Z - 1}}{{Z + 1}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{{\arcsin }}^{{ - 3}}}} \right. \times \\ \times \,\,\left. {\sqrt {\frac{2}{{Z + 1}}} + 137.3\left( {1 - \sqrt {\frac{{Z - 1}}{{Z + 1}}} } \right)} \right] \approx \\ \approx \,\,\frac{{1.931 \times {{{10}}^{{ - 3}}}{{e}^{2}}}}{{{{a}_{0}}\arcsin \sqrt {{2 \mathord{\left/ {\vphantom {2 {\left( {Z + 1} \right)}}} \right. \kern-0em} {\left( {Z + 1} \right)}}} }} \times \\ \times \,\,\left[ {{{Z}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{{\left( {\frac{{Z - 1}}{{Z + 1}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{{\arcsin }}^{{ - 3}}}\sqrt {\frac{2}{{Z + 1}}} + \frac{{137.3}}{{Z + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \right]. \\ \end{gathered} $

Молекулярный орбитальный момент полагаем равным нулю ($\lambda = 0$).

В табл. 1 приведено сравнение рассчитанных по (28) и (29) величин и экспериментальных данных [19, 20] для гидридов атомов второго периода, свидетельствующее о хорошей точности теории по длинам связей (расхождение около 1%) и неплохой оценке величины энергии.

Таблица 1.

Расчет длины и энергии связи в гидридах атомов 2-го периода

Соединение	Атомный номер Z	Длина связи, нм		Энергия связи, кДж/моль
Соединение	Атомный номер Z	расчет по (28)	эксперимент [19, 20]	расчет по (29)	эксперимент [19, 20]
HLi	3	0.1567	0.1595	277	234
HBe	4	0.1366	0.1343	270	250
HB	5	0.1228	0.1232	286	334
HC	6	0.1125	0.1120	323	338
HN	7	0.1045	0.1038	382	367
HO	8	0.0980	0.0971	463	428
HF	9	0.0925	0.0917	567	569

Общий случай гидридов

Подстановка (25) в (28) даст общую формулу для гидридов – молекул типа HX (X – атом из n-го периода Периодической таблицы Менделеева с атомным номером Z):

(30)

${{r}_{{{\text{HX}}}}} = 3.771{{a}_{0}}\arcsin \sqrt {\frac{{2{{{\left( {n - 1} \right)}}^{2}} - \sqrt 2 \left( {n - 2} \right)}}{{Z + 1}}} .$

На рис. 2 демонстрируется соответствие результатов расчета по формуле (30) экспериментальным значениям длин связей в гидридах [19, 20]. Приведены данные для 32 соединений с водородом элементов 2–6-го периодов.

Рис. 2.

Сравнение результатов теоретического расчета по формуле (30) со справочными данными для 32 молекул гидридов атомов 2-го–6-го периодов Периодической таблицы химических элементов. Обозначения: (+) – гидриды элементов с атомными номерами 3, 4, 5, 6, 7, 8, 9, 14, 15, 16, 17, 25, 30, 32, 33, 34, 35, 48, 50, 51, 53, 80; (о) – гидриды элементов с атомными номерами 12, 13, 24, 27, 29, 46, 47, 49, 79, 81 (указаны на графике).

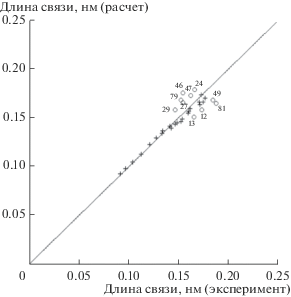
На рис. 2 при росте длины связи выше 0.15 нм наблюдается уширение области точек, которое достигает 10% в обе стороны от диагонали. Это область больших длин связи, сопоставимых с радиусом экранирования, где нарушается условие ${{r}_{e}} \ll {{r}_{s}},$ примененное для факторизации функции связи. Для уточнения модели в этой области потребуется рассмотреть более сложный вид функции связи. Вероятно, функция связи с ростом аргумента убывает быстрее, чем косинус в (10), и в таком случае здесь проявляется тенденция, обусловленная переходом к более выраженным ионным соединениям, размер которых зависит от знака заряда ионов и колеблется относительно длины связи полярных соединений, найденной по предложенной модели. Хорошо известно, что в ионных соединениях, где водород представлен в виде протона, межъядерное расстояние существенно меньше, чем в тех соединениях, где водороду принадлежат два электрона. В соответствии с графиком можно предположить, что в гидридах атомы главных подгрупп: Al, In, Mg, Tl – окислены, а переходные элементы: Ag, Au, Cr, Co, Cu, Pd – восстановлены.

Подстановка формул (25), (30) в (18), (19) при $\lambda = 0$ позволяет вычислить энергию гидридов (рис. 3).

Рис. 3.

Наложение экспериментальных точек [19, 20] на теоретические графики в координатах x, y (14, 15). Линия 1 построена по уравнению (13) для гомополярных соединений; на ней показана точка молекулы водорода (сравнить с рис. 1). Линия 2, построенная по уравнениям (28), (29), соответствует гидридам атомов 2-го периода. Линия 3, построенная по формулам для длины (30) и энергии связи (18) при подстановке (19), (25), (30), соответствует гидридам элементов 3-го периода.

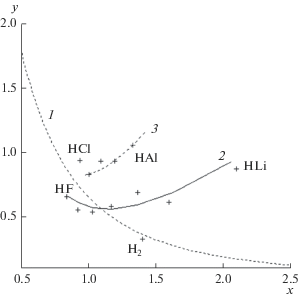
Для гидридов атомов других периодов закономерность, выражаемая уравнением (18), нарушается по ряду причин (значимый энергетический вклад акцептора, ненулевой орбитальный момент и др.), рассмотрение которых мы отложим на будущее.

ЗАКЛЮЧЕНИЕ

С помощью теории обобщенных зарядов (теории, вводящей обобщенный заряд молекулярного фрагмента как величину, пропорциональную его потенциальной энергии) получены соотношения, позволяющие связать длину и энергию межатомных связей с атомными номерами, кратностью связи и молекулярным орбитальным моментом. Обобщенный заряд является характеристикой электронного множества, общего для атомов жесткого молекулярного фрагмента. Число электронов этого множества ограничено эффектом экранирования, ставящим участие электронов в межатомном взаимодействии в соответствие с их локализацией и энергией. Помимо обобщенного заряда в ТОЗ используется понятие “функции связи”, определяемой через обобщенные заряды связываемых атомов и электрические заряды их ядер, зависящей от параметров ковалентной связи. Связь через величины обобщенных зарядов электронного строения, энергии взаимодействия атомов и равновесного расстояния между ними выражается в виде уравнений для гомополярных и полярных соединений.

Рассмотрены особенности описания донорно-акцепторной связи, сочетающей в себе черты гомополярной ковалентной и ионной связи. Найдены закономерности для донорно-акцепторной связи и, как следствие, получены выражения через атомный номер для длины и энергии гидридов. Сравнение расчетных и экспериментальных данных для гидридов элементов первых периодов показало удовлетворительную корреляцию.

БЛАГОДАРНОСТЬ

Работа выполнена при финансовой поддержке РФФИ (грант 18-03-00382а).

Список литературы

Каплан И.Г. Введение в теорию межмолекулярных взаимодействий. М.: Наука, 1982. 312 с.
Цирельсон В.Г. Квантовая химия. Молекулы, молекулярные системы и твердые тела. М.: БИНОМ, 2012. 496 с.
Koch W., Holthausen M.C. A Chemist’s Guide to Density Functional Theory. Second Edition, 2001, Wiley-VCH Verlag GmbH, 293 p.
Теория неоднородного электронного газа / Под ред. Лундквиста С.С., Марча Н. М.: Мир, 1987. 400 с.
Dolgonosov A.M. // Russ. J. Inorg. Chem. 2000. V. 45 P. 997. [Долгоносов А.М. // Журн. неорган. химии. 2000. Т. 45. № 6. С. 997.]
Dolgonosov A.M. // Russ. J. Phys. Chem. 2000. V. 74. Suppl. 2. P. S324.
Dolgonosov A.M. // Russ. J. Phys. Chem. A. 2008. V. 82. P. 2079. [Долгоносов А.М. // Журн. физ. химии. 2008. Т. 82. № 12. С. 2306.]
Долгоносов А.М. Модель электронного газа и теория обобщенных зарядов для описания межатомных взаимодействий и адсорбции. М.: ЛИБРОКОМ, 2009. 167 с.
Dolgonosov A.M. // Russ. J. Phys. Chem. A. 2001. V. 75. P. 1659. [Долгоносов А.М. // Журн. физ. химии. 2001. Т. 75. № 10. С. 1813.]
Dolgonosov A.M. // Russ. J. Phys. Chem. A. 2002. V. 76. P. 993. [Долгоносов А.М. // Журн. физ. химии. 2002. Т. 76. № 6. С. 1107.]
Долгоносов А.М. Неспецифическая селективность в проблеме моделирования высокоэффективной хроматографии. М.: КРАСАНД, 2012. 256 с.
Авгуль Н.Н., Киселев А.В., Пошкус Д.П. Адсорбция газов и паров на однородных поверхностях. М.: Химия, 1975. 384 с.
Pertsin A.I., Kitaigorodsky A.I. The atom-atom potential method in the physics and chemistry of organic molecular solids. Berlin, N.Y., Tokyo: Springer Verlag, 1986.
Dolgonosov A.M. // Russ. Chem. Bull. 2016. V. 65. P. 952. [Долгоносов А.М. // Изв. АН. Сер. хим. 2016. № 4. С. 952.]
Dolgonosov A.M. // Russ. J. Phys. Chem. 2003. V. 77. P. 764. [Долгоносов А.М. // Журн. физ. химии. 2003. Т. 77. № 5. С. 856.]
Dolgonosov A.M. // Russ. J. Inorg. Chem. 2015. V. 60. P. 194. [Долгоносов А.М. // Журн. неорган. химии. 2015. Т. 60. № 2. С. 233.].
Dolgonosov A.M. // Russ. J. Inorg. Chem. 2017. V. 62. № 3. P. 344. [Долгоносов А.М. // Журн. неорган. химии. 2017. Т. 62. № 3. С. 330.]
Dolgonosov A.M. // Russ. J. Phys.Chem. 2002. V. 76. № 12. P. 2015. [Долгоносов А.М. // Журн. физ. химии. 2002. Т. 76. № 12. С. 2216.]
Молекулярные постоянные неорганических соединений: Справочник / Под ред. Краснова К.С. Л.: Химия, 1979. 448 с.
CRC Handbook of Chemistry and Physics / Ed. Lide D.R. Internet Version, http://www.hbcpnetbase.com, CRC Press, Boca Raton, FL, 2005.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал