1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 65, № 8, 2020

Журнал неорганической химии, 2020, T. 65, № 8, стр. 1073-1081

Магнитные свойства хиральных золотых нанотрубок

П. Н. Дьячков a, *, Е. П. Дьячков a

a Институт общей и неорганической химии им. Н.С. Курнакова РАН
119991 Москва, Ленинский пр-т, 31, Россия

* E-mail: p_dyachkov@rambler.ru

Поступила в редакцию 27.01.2020
После доработки 27.02.2020
Принята к публикации 29.02.2020

Полный текст (PDF)

Аннотация

Рассчитаны магнитные поля, генерируемые наносоленоидами на основе золотых нанотрубок. Энергетические уровни электронов в нанотрубках рассчитаны с использованием метода линеаризованных присоединенных цилиндрических волн с циклическими граничными условиями Борна–фон Кармана и с учетом винтовой симметрии трубок. Определены числа проводящих каналов, низкотемпературные туннельные электронные токи и магнитные поля в наносоленоидах на основе золотых нанотрубок различной длины и структуры. Результаты свидетельствуют о том, что хиральные золотые нанотрубки являются перспективными материалами для создания наносоленоидов с сильными магнитными полями и могут быть использованы для более реалистичного дизайна нано-соленоидов.

Ключевые слова: хиральность, магнитные свойства, наносоленоиды, моделирование

ВВЕДЕНИЕ

Развитие нанотехнологий приводит к миниатюризации электронных устройств и их компонентов, что инициирует, в частности, интерес к конструированию наномасштабных электромагнитов и индукторов, в которых винтовые потоки электронов через нанопровод будут генерировать магнитное поле. Было высказано предположение о том, что в качестве наносоленоидов могут служить хиральные нанотрубки [1–8]. Наиболее известные идеальные углеродные (n1, n2) нанотрубки не подходят для этого, поскольку для создания соленоидов требуются материалы с металлическим типом проводимости, а углеродные нанотрубки являются либо диэлектриками, либо квазиметаллическими материалами в зависимости от строения (индексов n1 и n2) [9–11]. Более пригодны оказались химически модифицированные гетеронанотрубки, которые образованы связанными спиральными лентами из углерода и нитрида бора [1], а также некоторые углеродные нанотрубки, скрученные в виде спиралей с очень сложной (возможно нереалистичной) геометрией [6, 7]. Ожидается, что относительно мощные магнитные поля могут быть получены на композитах из углеродных нанотрубок и меди [8].

Предыдущие расчеты зонной структуры показывают, что все золотые нанотрубки, независимо от их геометрии, обладают металлической проводимостью с большими числами каналов проводимости, потому они могут быть пригодны для дизайна наносоленоидов [11–13]. Еще в 2003 г. хиральные золотые нанотрубки (5, 3) длиной 5 нм были успешно синтезированы с помощью электронно-лучевого истончения золотой фольги в электронном микроскопе [14]. За последние годы достигнут значительный прогресс в синтезе золотых нанотрубок и кластеров и существенно увеличилось количество информации об их свойствах. К настоящему моменту в литературе с разной степенью полноты описаны электронные, электрические, оптические, электрохимические, транспортные и каталитические свойства золотых нанотрубок [15–28]. В недавнем обзоре появилась информация об их использовании для решения проблем разделения энантиомеров, белков, для иммунохимического анализа, обнаружения ДНК и фототермической абляции клеток [18].

Цель данной работы – расчет магнитных полей, генерируемых хиральными золотыми нанотрубками при прохождении электрического тока. Мы предполагаем, что электрический ток в золотых хиральных нанотрубках течет только по направлению винтовых трансляций. Это предположение согласуется с предыдущими исследованиями индукции хирального тока, магнетодинамики, хиральной проводимости и самоиндукции в углеродных нанотрубках и винтовых молекулярных системах [29–34]. Заметим также, что для хиральных трубок Fe (5, 3) и (6, 3) в работе [35] приведен явный вид распределения электронной плотности (квадраты собственных волновых функций) для проводящих состояний на уровне Ферми, который четко иллюстрирует наличие винтовых каналов переноса хирального электронного тока в нанотрубках.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Неограниченные по длине нанотрубки

В хиральной нанотрубке электронный транспорт вдоль ее оси сопровождается циклическим вращением электронов вокруг этой оси, что вызывает появление циклической компоненты тока и приводит к генерации магнитного поля (рис. 1). Согласно закону Ампера, для соленоида неограниченной длины магнитное поле B = μ0νj = 4π × 10–7νj внутри соленоида не зависит от его диаметра и расстояния от оси, а определяется только величиной тока j и числом ν оборотов тока вокруг оси соленоида в расчете на единицу длины. Снаружи поле нулевое. Величина ν определяется геометрией трубки.

Рис. 1.

Золотая нанотрубка в контакте с двумя электродами, линии магнитного поля и цилиндрическая система координат.

Атомная геометрия одностенных золотых нанотрубок напоминает геометрию углеродных. Достаточно гексагональную сетку из атомов C заменить треугольной сеткой из атомов Au с длинами связей dAu–Au = 2.9 Å. Золотые трубки обладают симметрией относительно винтовых трансляций S(hz, ω), которые представляют собой сдвиги вдоль оси z трубки на расстояние hz с одновременным поворотом на угол ω, величины которых определяются индексами n1 и n2 [11]. Из-за винтовой симметрии хиральных трубок поворот на угол 2π сопровождается 2π/ω сдвигами на расстояние, равное hz(2π/ω). Поэтому число круговых токов на единицу длины в хиральной нанотрубке ν = = nω/(2πhz), где n отражает присутствие n эквивалентных цепочек из атомов Au в трубках с вращательной осью порядка n (n равняется наибольшему общему делителю индексов n1 и n2). Параметры структуры, включая значения ν и n для золотых трубок различной хиральности и диаметра, приведены в табл. 1.

Таблица 1.  

Параметры структуры и магнитное поле неограниченных наносоленоидов на основе некоторых хиральных золотых нанотрубок

n1, n2 n hz, Å ω, рад ν, 1/Å NF B/U, Tл/B
(5, 1) 1 0.548 5.168 1.820 6 10.9
(5, 2) 1 0.950 0.281 1.050 7 7.35
(5, 3) 1 0.578 3.910 1.730 8 13.8
(5, 4) 1 1.450 1.390 0.688 9 6.19
(10, 1) 1 0.263 5.688 3.800 11 41.8
(10, 2) 2 1.100 2.584 0.912 12 21.8
(10, 3) 1 0.696 1.921 1.440 13 18.7
(10, 4) 2 1.900 1.329 0.524 14 14.7
(10, 5) 5 7.380 0.808 0.135 15 10.1
(10, 6) 2 1.150 1.955 0.876 16 27.7
(10, 7) 1 0.240 4.433 4.150 17 70.6
(10, 8) 2 2.900 0.695 0.344 18 12.4
(10, 9) 1 1.450 0.661 0.689 19 13.1
(12, 2) 2 0.900 2.667 1.110 14 30.8
(11, 3) 1 0.307 4.028 3.260 14 45.6
(8, 7) 1 1.450 0.837 0.690 15 10.4
(13, 8) 1 0.220 3.887 4.520 21 96.2
(17, 10) 1 0.359 1.860 2.790 27 75.3
(18, 11) 1 0.137 4.549 7.310 29 212

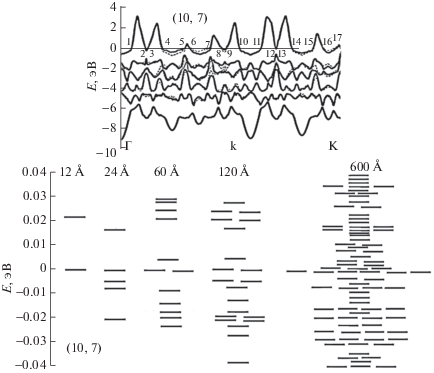
При описании и оценке токов необходимо отметить, что в золотых нанотрубках наблюдается баллистический механизм электронного транспорта, когда электроны туннелируют между катодом и анодом сквозь наноматериал [36]. Этот механизм определяется типичными размерами трубок: длина свободного пробега электронов больше, чем длина самой нанотрубки. Баллистический перенос электронов описывается формализмом Ландауэра [27, 36, 37], и при низких температурах ток рассчитывается по уравнению j = G0NFU, где U ‒ приложенное напряжение, а NF ‒ число каналов проводимости, которое определяется электронной структурой материала, а именно: NF равняется числу точек пересечения электронных зон с уровнем Ферми. Константа G0 = 2e2/h = 7.748 × 10–5 Ом–1, где e ‒ заряд электрона и h ‒ постоянная Планка, называется квантом проводимости; она равна току при U = 1 В в материале с одним проводящим состоянием на уровне Ферми. Расчеты электронной структуры золотых нанотрубок неограниченной длины, выполненные ранее методом линеаризованных присоединенных цилиндрических волн [11‒13, 38‒40] с учетом циклических граничных условий Борна–фон Кармана и винтовой геометрии трубок, показывают, что для NF приближенно справедливо соотношение NF ≈ n1 + n2. Зонные структуры нанотрубок (5, 3), (10, 1) и (10, 7) служат иллюстрацией этого правила (рис. 2‒4).

Рис. 2.

Зонная структура бесконечной (а) и конечных (б) золотых нанотрубок (5, 3) длиной 12–600 Å. Здесь и далее начало отсчета энергии расположено на верхних занятых уровнях; для бесконечной трубки приведена полная зонная структура, а для конечных ‒ только уровни вблизи E = 0.

Рис. 3.

Зонная структура золотых нанотрубок (10, 1).

Рис. 4.

Зонная структура золотых нанотрубок (10, 7).

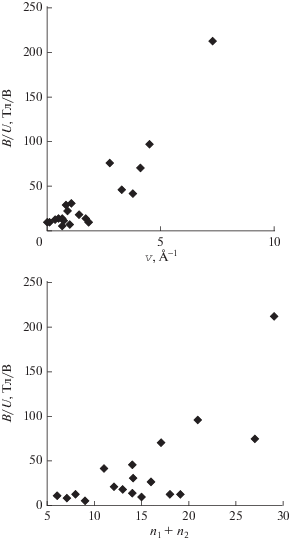
Суммируя результаты и подставляя в формулу для расчета индукции магнитного поля число витков тока в расчете на 1 Å как ν, получаем окончательно B(Tл) = n0.974ν(Å–1)NFU(В) ≈ ≈ nν(Å–1)NFU(В) ≈ nν(Å–1)(n1 + n2)U(В). Численные значения поля внутри неограниченных золотых нанотрубок приведены в последнем столбце табл. 1. Можно видеть, что значения B в золотых трубках ряда (5, n2) лежат в интервале 6.1‒13.8 Тл/B, они возрастают за счет увеличения числа каналов проводимости и числа витков тока до 13.1‒70.6 Тл/B при переходе к нанотрубкам ряда (10, n2) большего радиуса. Дальнейшее возрастание индексов n1 и n2 приводит к еще большему росту магнитного поля внутри золотых трубок вплоть до 212 Тл/В (рис. 5). Значения магнитных полей в рассчитанных здесь золотых нанотрубках на 1‒2 порядка больше, чем теоретические величины полей в изученных ранее наносоленоидах, где величины B около 1 Тл/B [1‒8].

Рис. 5.

Зависимости магнитного поля в неограниченных золотых нанотрубках от характеристик их геометрии.

Нанотрубки конечной длины

Обсудим магнитные поля для более реалистичного случая нанотрубок конечной длины. Магнитное поле конечных соленоидов заметно сложнее. Оно описывается в терминах цилиндрических координат z, r, θ. В силу цилиндрической геометрии нанотрубок, поле по-прежнему не зависит от θ, а радиальная и осевая компоненты поля описываются формулами [41, 42]:

$\begin{gathered} {{B}_{r}} = {\text{\;}} - \frac{{a{{{\mu }}_{0}}{v}j}}{{2\pi }} \times \\ \times \,\mathop \smallint \limits_0^\pi \left[ {\frac{{\cos {\theta }d{\theta }}}{{{{r}^{2}}\, + \,{{a}^{2}}\, - \,2ar{\kern 1pt} \cos \theta {{{[z\, - \,{{L}^{2}}\, + \,{{r}^{2}}\, + \,{{a}^{2}}\, - \,2ar{\kern 1pt} \cos {\theta }]}}^{{1{\text{/}}2}}}}}} \right]_{{{{\xi }_{ - }}}}^{{{{\xi }^{ + }}}} \\ \end{gathered} $
$\begin{gathered} {{B}_{r}} = {\text{\;}} - \frac{{a{{{\mu }}_{0}}{v}j}}{{2\pi }} \times \\ \times \,\mathop \smallint \limits_0^\pi \left[ {\frac{{{\xi }a{\text{\;}} - {\text{\;}}r\cos {\theta }d{\theta }}}{{{{r}^{2}}\, + \,{{a}^{2}}\, - \,2ar{\kern 1pt} \cos {\theta }{{{[z\, - \,{{L}^{2}}\, + \,{{r}^{2}}\, + \,{{a}^{2}}\, - \,2ar{\kern 1pt} \cos {\theta }]}}^{{1{\text{/}}2}}}}}} \right]_{{{{\xi }_{ - }}}}^{{{{\xi }^{ + }}}}, \\ \end{gathered} $
где a – радиус трубки, L – ее длина и ξ± = z ± L/2, μ0 – магнитная проницаемость. Численные результаты получаются интегрированием этих уравнений на компьютере.

Величины токов в трубках как бесконечной, так и конечной длины определяются туннелированием электронов сквозь нанотрубку. Но при переходе от одних к другим непрерывные дисперсионные электронные кривые сменяются дискретным электронным спектром, и числа каналов проводимости NF резко убывают, как видно на примере пятнадцати трубок (5, 3), (7, 6) и (10, 7) длиной 12‒600 Å (рис. 2‒4). В трубках (5, 3) с длиной L = 12 и 24 Å существует один такой уровень (NF = 1). В трубках (5, 3) с L = 60 и 120 Å соответственно NF = 2 и 3, что во всех случаях значительно меньше, чем NF = 8 для бесконечной (5, 3) золотой нанотрубки (табл. 2). Пропорционально уменьшению значений NF в 8, 4 и 2.7 раза должен уменьшаться ток при переходе к коротким (5, 3) нанотрубкам. В (5, 3) золотых нанотрубках длиной 600 Å значение NF = 7 приближается к значению NF = 8 для бесконечной трубки. Качественно такие же зависимости числа каналов проводимости от длины наблюдаются и для нанотрубок (10, 1) и (10, 7).

Таблица 2.  

Число каналов NF при различной длине L золотых нанотрубок разных хиральностей

n1, n2 Длина, Å
12 24 60 120 600 ∞
(5, 3) 1 1 2 3 7 8
(10, 1) 1 1 1 2 2 11
(10, 7) 1 1 2 2 6 17

На рис. 6 показаны зависимости магнитного поля от координат z и ρ для нанотрубок (5, 3), (10, 1) и (10, 7) длиной 12‒600 Å. Например, в нанотрубке (5, 3) из-за увеличения числа каналов проводимости с увеличением длины трубки внутреннее магнитное поле постепенно возрастает от 1.6 Тл/В в трубках длиной 12 и 24 Å до 3, 5 и 12 Тл/В в трубках с L = 60, 120 и 600 Å, медленно приближаясь к магнитному полю 13.8 Tл/В бесконечной (5, 3) трубки. В свободном пространстве внутри конечных канальцев магнитное поле зависит от расстояния r от оси трубки и от координаты z. На расстоянии около 5 Å от конца трубок (около z = L/2 – 5 Å) это поле начинает быстро падать, уменьшаясь вдвое при z = L/2 и практически обнуляясь вблизи z = L/2 + 5 Å. Поле снаружи трубок слабое, но не нулевое, как в случае бесконечной трубки. Оно минимально при z = 0 и достигает максимума на краю при z = L/2, где оно в 3‒4 раза меньше внутреннего поля. Характер вариаций магнитного поля в зависимости от координат z и r в конечных нанотрубках (10, 1) и (10, 7) большего диаметра аналогичен. Здесь поле также быстро убывает с укорочением нанотрубок, причем в самых коротких трубках с L = 12 и 24 Å и только единственным каналом проводимости максимальные значения поля B ≈ 1.5 Тл/В в центре трубок почти одинаковы независимо от геометрии трубок.

Рис. 6.

Магнитное поле конечных золотых нанотрубок (5, 3), (10, 1) и (10, 7); вставки показывают поле около краев трех более длинных трубок. Линии поля рассчитаны для свободного пространства, ограниченного ван-дер-ваальсовыми размерами трубок, и пронумерованы в порядке возрастания координаты r. Пунктирные линии обозначают край трубок. В центре нанотрубок z = 0: 1) r = 0 соответствует оси нанотрубок; 2) r = (a – rvdW)/2 соответствует положению между осью и внутренней ван-дер-ваальсовой границей трубок, где rvdW = 0.9 Å – ван-дер-ваальсов радиус атома золота; 3) r = a – rvdW – внутренняя ван-дер-ваальсова граница нанотрубок; 4) для r = a поле рассчитано при z ≥ L/2 + + rvdW, т.е. за пределами края трубок; 5) r = a + rvdW – внешняя ван-дер-ваальсова граница нанотрубок; кривые 6, 7 и 8 соответствуют внешнему свободному пространству на расстояниях 1, 2, 3 Å от границы трубок.

Самоиндукция

Помимо магнитного поля конечные соленоиды характеризуются самоиндукцией ℒ, которая рассчитывается по формуле: ℒ = μ0ν2SL. Самоиндукция зависит только от длины L и площади поперечного сечения S = πa2 соленоидов, но не от тока или рабочего напряжения. Она пропорциональна длине нанотрубки и ℒ(Гн) = 1.1 × 10–13L, 1.4 × × 10–12L и 3.1 × 10–13L(Å) для нанотрубок (5, 3), (10, 1) и (10, 7) соответственно.

ЗАКЛЮЧЕНИЕ

Рассчитаны магнитные поля в хиральных золотых нанотрубках. Установлены зависимости между геометрией и длиной трубок, уровнями энергии электронов, баллистическим электронным транспортом и магнитными полями, генерируемыми в них при прохождении постоянного электрического тока. Хиральные золотые нанотрубки являются перспективными материалами для создания наносоленоидов с сильными магнитными полями.

Список литературы

  1. Zhang Z.Y., Miao C., Guo W. // Nanoscale. 2013. V. 23. P. 11902. https://doi.org/10.1039/c3nr02914

  2. Xu F., Sadrzadeh A., Xu Z., Yakobson B.I. // Comput. Mater. Sci. 2014. V. 83. P. 426. https://doi.org/10.1016/j.commatsci.2013.11.043

  3. Xu F., Yu H., Sadrzadeh A., Yakobson B.I. // Nano Lett. 2016. V. 16. P. 34. https://doi.org/10.1021/acs.nanolett.6b01822

  4. Mitran T.L., Nemnes G.A. // RSC Adv. 2017. V. 7. P. 49е041. https://doi.org/10.1039/c7ra08247a

  5. Avdoshenko S.M., Koskinen P., Sevinçli H. et al. // Sci. Rep. 2013. V. 3. P. 1632. https://doi.org/10.1038/srep01632

  6. Popović Z.P., Vuković T., Nikolić B. et al. // Contemp. Mater. 2017. V. 8. № 2. P. 122. https://doi.org/10.7251/COMEN1702121P

  7. Браже Р.A., Савин A.Ф. // Физика волновых процессов и радиотехнические системы. 2015. Т. 18. № 1. C. 50. https://journals.ssau.ru/index.php/pwp/article/viewFile/7211/7072

  8. James C.R., Long J.E., Manning D.E. // Sci. Rep. 2019. V. 9. P. 143. https://doi.org/10.1038/s41598-018-38306-8

  9. Ouyang M., Huang J.-L., Cheung C.L. et al. // Science. 2001. V. 292. P. 702. https://doi.org/10.1126/science.1058853

  10. D’yachkov P.N. // Russ. J. Inorg. Chem. 2018. V. 63. № 1. P. 55. [Дьячков П.Н. // Журн. неорган. химии. 2018. Т. 63. № 1. С. 60.]https://doi.org/10.1134/S0036023618010072

  11. Khoroshavin L.O., Krasnov D.O., D’yachkov P.N., Kol’tsova E.M. // Russ. J. Inorg. Chem. 2017. V. 62. № 6. P. 783. [Хорошавин Л.O., Краснов Д.O., Дьячков П.Н., Кольцова Э.M. // Журн. неорган. химии. 2017. Т. 62. № 6. С. 800.]https://doi.org/10.1134/S0036023617060110

  12. D’yachkov E.P., D’yachkov P.N. // J. Phys. Chem. C. 2019. V. 123. P. 26005. https://doi.org/10.1021/acs.jpcc.9b07610

  13. Krasnov D.O., Khoroshavin L.O., D’yachkov P.N. // Russ. J. Inorg. Chem. 2019. V. 64. № 1. P. 108. https://doi.org/10.1134/S0036023619010145

  14. Oshima Y., Onga A., Takayanagi K. // Phys. Rev. Lett. 2003. V. 91. P. 205503. https://doi.org/10.1103/PhysRevLett.91.205503

  15. Bridges C.R., DiCarmine P.M., Fokina A. et al. // J. Mater. Chem. A. 2013. V. 1. P. 1127. https://doi.org/10.1039/C2TA00729K

  16. Bridges C.R., DiCarmine P.M., Seferos D.S. // Chem. Mater. 2012. V. 24. P. 963. https://doi.org/10.1021/cm203184d

  17. Hendren W.R., Murph A., Evans P. et al. // J. Phys.: Condens. Matter. 2008. V. 20. P. 362203. https://doi.org/10.1088/0953-8984/20/36/362203

  18. Shamraiz U., Raza B., Hussain H. et al. // Intern. Mater. Rev. 2018. P. 1743. https://doi.org/10.1080/09506608.2018.1554991

  19. Ye S., Marston G., McLaughlan J.R. et al. // Adv. Funct. Mater. 2015. P. 1. https://doi.org/10.1002/adfm.201404358

  20. Ye S., Marston G., Markham A.F. et al. // IOP Conf. Series: J. Phys.: Conf. Series. 2019. V. 1151. P. 012018. https://doi.org/10.1088/1742-6596/1151/1/012018

  21. Kondo Y., Takayanagi K. // Science. 2000. V. 289. P. 606. https://doi.org/10.1126/science.289.5479.606

  22. Kohl J., Fireman M., O’Carroll D.M. // Phys. Rev. B. 2011. V. 84. P. 235118. https://doi.org/10.1103/PhysRevB.84.235118

  23. Wang J., Zhang C., Zhang J. et al. // Adv. Optical Mater. 2016. V. 5. № 4. P. 1. https://doi.org/10.1002/adom.201600731

  24. Zhu L., Wang J., Ding F. // J. Chem. Phys. 2009. V. 130. P. 064706. https://doi.org/10.1063/1.3055520

  25. Sen A., Lin C.J., Kaun C.C. // J. Phys. Chem. C. 2013. V. 117. P. 13676. https://doi.org/10.1021/jp402531p

  26. Zhang K., Zhang H. // J. Phys. Chem. C. 2014. V. 118. P. 635. https://doi.org/10.1021/jp410056u

  27. Mironov G.I. // Russ. J. Inorg. Chem. 2019. V. 64. № 10. P. 1257. [Миронов Г.И. // Журн. неорган. химии. 2019. Т. 64. № 10. С. 1064.]https://doi.org/10.1134/S0036023619100097

  28. Mironov G.I. // Russ. J. Inorg. Chem. 2018. V. 63. № 1. P. 66. [Миронов Г.И. // Журн. неорган. химии. 2018. Т. 63. № 1. С. 72.]https://doi.org/10.1134/S0036023618010114

  29. Miyamoto Y., Louie S.G., Cohen M.L. // Phys. Rev. Lett. 1996. V. 76. P. 2121. https://doi.org/10.1103/PhysRevLett.76.2121

  30. Miyamoto Y., Rubio A., Louie S.G., Cohen M.L. // Phys. Rev. B. 1999. V. 60. № 19. P. 13885. https://doi.org/10.1103/PhysRevB.60.13885

  31. Miyamoto Y. // Phys Rev. B. 1996. V. 54. P. R11149

  32. Krstic V., Wagniere G., Rikken G.L. // Chem. Phys. Lett. 2004. V. 390. P. 25. https://doi.org/10.1016/j.cplett.2004.03.133

  33. Lambert C.J., Bailey S.W.D., Cserti J. // Phys Rev. B. 2008. V. 78. P. 233405. https://doi.org/10.1103/PhysRevB.78.233405

  34. Gutierrez R., Díaz E., Naaman R., Cuniberti G. // Phys. Rev. B. 2012. V. 85. P. 081404(R). https://doi.org/10.1103/PhysRevB.85.081404

  35. Shimada T., Okuno J., Kitamura T. // Nano Lett. 2013. V. 13. № 6. P. 2792. https://doi.org/10.1021/nl401047z

  36. Landauer R. // Phil. Mag. 1972. V. 21. P. 863. https://doi.org/10.1080/14786437008238472

  37. Chen A.-B. // Handbook of Theoretical and Computational Nanotechno-logy / Eds. Rieth M., Schommers W. California: American Scientific Publishers, 2006. V. 1. P. 311.

  38. D’yachkov P.N. // Quantum Chemistry of Nanotubes: Electronic Cylindrical Waves. London: CRC Press, 2019. 212 p.

  39. D’yachkov P.N., Makaev D.V. // Phys. Rev. B. 2007. V. 76. P. 195411. https://doi.org/10.1103/PhysRevB.76.195411

  40. D’yachkov P.N., Makaev D.V. // Int. J. Quantum Chem. 2016. V. 116. P. 316. https://doi.org/10.1002/qua.25030

  41. Callaghan E., Maslen S. // The Magnetic Field of a Finite Solenoid. Washington: National Aeronautics and Space Administration, 1960.

  42. Caciagli A., Baars R.J., Philipse A.P. et al. // J. Magn. Magn. Mater. 2018. V. 456. P. 423. https://doi.org/10.1016/j.jmmm.2018.02.003

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал