Журнал неорганической химии, 2020, T. 65, № 8, стр. 1082-1091
Теоретическое моделирование реакций присоединения молекулы H2 к магниевым кластерам Mg17L, допированным атомами переходных 3d-металлов
А. П. Мальцев a, b, *, О. П. Чаркин a, **
a Институт проблем химической физики РАН
142432 Московская обл., Черноголовка, пр-т Академика Семенова, 1, Россия
b Московский государственный университет им. М.В. Ломоносова
111991 Москва, Ленинские горы, 1, Россия
* E-mail: maltsevaleksej@gmail.com
** E-mail: charkin@icp.ac.ru
Поступила в редакцию 20.02.2020
После доработки 02.04.2020
Принята к публикации 04.04.2020
Аннотация
В рамках метода функционала плотности выполнены расчеты поверхности потенциальной энергии (ППЭ) элементарного каталитического цикла Mg17L + H2 гидрирования магниевых кластеров, допированных переходными металлами (L = Ti, V, Cr, Mn, Fe, Co). Локализованы особые точки ППЭ, отвечающие локальным минимумам интермедиатов и переходным состояниям вдоль минимального энергетического пути реакций. Рассчитаны энергетические, геометрические, спектроскопические параметры особых точек ППЭ. Проанализированы тенденции изменения каталитической активности допантов в ряду переходных 3d-металлов. Результаты сравниваются с данными предыдущих DFT-расчетов каталитического цикла гидрирования родственных реакций алюминиевых кластеров Al12L + H2 с теми же допантами L.
ВВЕДЕНИЕ
В течение длительного времени магний остается в числе перспективных материалов для хранения водорода [1] благодаря высокой емкости его гидридов, обратимости процессов сорбции–десорбции, доступности и дешевизне. Существенным недостатком магния является низкая скорость его реакций гидрирования и дегидрирования. Ускорению этих реакций способствуют добавление переходных металлов в качестве катализаторов, измельчение магниевых частиц до субмикронных [1–4] и другие подходы. К сожалению, достигнутые результаты в технологии не полностью соответствуют практическим требованиям, а экспериментальные исследования в области нано- и субнаноструктурированных материалов, где можно ожидать наилучшей кинетики, сталкиваются с техническими трудностями. В связи с этим в последние годы быстро растет интерес к исследованиям механизмов элементарных процессов сорбции–десорбции молекул водорода на поверхности субнаноразмерных допированных кластеров легких металлов. Эти исследования выполняются на молекулярном уровне с использованием квантово-химических расчетов в сочетании с измерениями методами масс-спектрометрии, фотоэлектронной и ИК-спектроскопии в инертных матрицах. К настоящему времени обнаружены и исследованы гидриды серии MgmHn, где m = 1–4 и n = 1–8 [5], смешанные магний-алюминиевые кластеры и их отрицательные ионы ${\text{A}}{{{\text{l}}}_{n}}{\text{Mg}}_{m}^{ - }$ (m ≤ 3, n + m ≤ 15) [6, 7]. Систематические расчеты, как правило, в рамках метода функционала плотности (МФП/DFT), выполнены для более широких семейств смешанных кластеров Mg28 –nAln (n = 0–28) [8] и гомоядерных изомеров Mgn (n = 2–56) [9, 10], у которых наиболее стабильными предсказаны нейтральные частицы Mg24Al4, Mg21Al7, Mg14Al14, Mg26Al2 и Mg27Al1; отрицательные ионы ${\text{A}}{{{\text{l}}}_{{\text{5}}}}{\text{Mg}}_{2}^{ - },$ ${\text{A}}{{{\text{l}}}_{{{\text{11}}}}}{\text{Mg}}_{3}^{ - },$ ${\text{A}}{{{\text{l}}}_{{\text{7}}}}{\text{Mg}}_{3}^{ - },$ ${\text{A}}{{{\text{l}}}_{{{\text{11}}}}}{\text{Mg}}_{2}^{ - }$ и “магические” кластеры Mg10 и Mg17 (см. подробнее работу [11]).
Особый интерес представляют исследования механизмов элементарных реакций водорода с кластерами легких металлов. Эта проблема подробно изучалась на примере реакций молекул Н2 с алюминиевыми кластерами Al12L, допированными атомами L переходных и непереходных периодов [12–18], в меньшей степени для магний-алюминиевых кластеров Mg5Al7Ni [19], кластеров MgnL (L = Rb, Co) [20, 21]. К сожалению, реакции гидрирования нано- и субнаноразмерных магниевых частиц остаются малоизученными. Из-за трудностей экспериментальных измерений имеющаяся информация в этой области в основном получена в рамках теоретического моделирования с использованием DFT-расчетов поверхностей потенциальной энергии (ППЭ) вдоль минимальных энергетических путей (МЭП) каталитических циклов, а также расчетами плотности состояний (DOS) для структур MgH2 [22–24].
В предыдущем сообщении [11] приведены данные расчетов ППЭ вдоль реакций гидрирования гомоядерного магниевого (Mg18) кластера, а также кластера Mg17Ni, допированного атомом никеля с разными положениями допанта Ni на поверхности и внутри магниевого каркаса:
(1)
${\text{M}}{{{\text{g}}}_{{18}}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{{\text{18}}}}}{{{\text{H}}}_{2}},$(2)
$\begin{gathered} {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}}{{{\text{H}}}_{2}} + {{{\text{H}}}_{2}} \to \\ \to {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}}{{{\text{H}}}_{4}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}}{{{\text{H}}}_{6}}. \\ \end{gathered} $Показано, что гидрирование гомоядерного кластера Mg18 (реакция (1)) сильно затруднено из-за высокого барьера сорбции (>30 ккал/моль). Замещение поверхностного атома Mg атомом допанта Ni снижает этот барьер до 4–5 ккал/моль. Энергия сорбции молекулы Н2 с образованием первичного дигидрида Mg17NiH2 оценивается в ∼12 ккал/моль у первого цикла и возрастает до 14 и далее до 16 ккал/моль при увеличении числа циклов в реакции (2). Следующая за сорбцией стадия “очистки” допанта (dopant cleaning) связана с разрывом связей Ni−H в первичном дигидриде, удалением обоих связанных атомов Н от допанта и образованием вторичного дигидрида, в котором допанты расположены в мостиковых позициях над соседними ребрами (Mg–Mg) или гранями магниевого каркаса, а “очищенный” допант при этом восстановил готовность к началу нового цикла. У всех ступеней реакции (2) стадия “очистки” допанта оказывается критической, отвечающие ей барьеры оцениваются в ∼10–12 ккал/моль.
Настоящая работа является продолжением [11] и посвящена DFT-расчетам ППЭ родственных каталитических реакций:
(2а)
${\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{L}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{L}}{{{\text{H}}}_{2}}$присоединения молекулы Н2 к магниевым кластерам, допированным атомами L(3d) металлов первого переходного периода (L = Ti, V, Cr, Mn, Fe, Co).
Цель работы – определение геометрических, колебательных, энергетических и электронных характеристик интермедиатов и переходных состояний вдоль МЭП этих реакций, оценка активационных барьеров и изменений энергии на их ключевых стадиях, анализ влияния природы допанта на поведение этих характеристик при изменении L(3d) вдоль периода.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Каталитический цикл реакции (2а) подробно описан в [11]. Расчеты выполняли с использованием программы Gaussian-09 [25] и метода BP86 [26] с базисом 6-31G*. Оптимизацию геометрии особых точек ППЭ (переходных состояний и интермедиатов) проводили для состояний с различной мультиплетностью M = 2S + 1, их характер определяли с помощью расчетов частот нормальных колебаний и c использованием метода внутренней координаты реакции (irc). В настоящем сообщении исследование сфокусировано на состояниях с наиболее низкой полной энергией. На примере цикла Mg17Ni + H2 критические точки ППЭ были пересчитаны с базисом 6-31G**. Найдено, что включение поляризующих функций атомов Н привело к незначительным уточнениям относительных энергий и барьеров по сравнению с базисом 6-31G*, что практически не сказывается на результатах настоящей работы. Различия не превышают ~1.0–1.5 ккал/моль во второй половине цикла (интервал структур Е–F–G–H–I) и слегка увеличиваются в его начале, причем барьер (D) между μ-Н2-комплексом (C) и дигидридом Mg17NiH2 (Е) остается малым в расчетах с обоими базисами.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Кластеры Mg17L c допантом L(3d) на поверхности магниевого каркаса
На рис. 1 изображена типичная структура изолированного кластера Mg17L с допантом L(3d) на поверхности каркаса Mg17, в котором допант связан радиальной связью L–Mg(с) с центральным атомом Mg(с) и тангенциальными связями L–Mg(t) с пятью соседними поверхностными атомами Mg(1, 2, 10, 15, 17). В табл. 1 приведены равновесные длины связей допанта с соседними атомами магния (R, Å), частоты радиальных и тангенциальных валентных колебаний (ν, см–1), спиновые плотности на атоме допанта (ρs(L)) в долях е, относительные энергии состояний с разной мультиплетностью (ΔErel(M), ккал/моль), а также энергии связи допанта с каркасом (D(L), ккал/моль), отвечающие реакциям Mg17L → Mg17 + L, в которых исходные кластеры и продукты распада находятся в своих основных спиновых состояниях. У эндоэдрального изомера допант расположен вблизи центра кластера с небольшими смещениями в сторону ребра или грани, ему отвечают самые низкие частоты внутренних колебаний и слабое взаимодействие с атомами каркаса. Эндоэдральный изомер везде на несколько десятков ккал/моль менее выгоден по сравнению с экзоэдральным и в настоящей статье не рассматривается.
Рис. 1.
Оптимизированная структура допированного кластера Mg17L с допантом на поверхности магниевого каркаса.
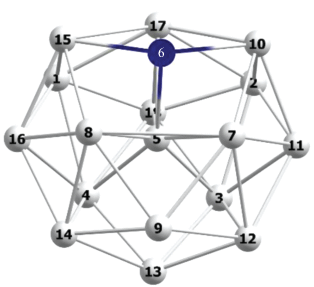
Таблица 1.
Рассчитанные характеристики кластеров Mg17L c допантом на поверхности магниевого кластера
| L | M | R, Å L–Mg(c) |
νa, см–1 L–Mg(c) |
R, Å L–Mg(t) |
νa, см–1 L–Mg(t) |
ρs(L)b | ΔErel(M), ккал/моль |
D(L)c, ккал/моль |
|---|---|---|---|---|---|---|---|---|
| Mg | 1 | 3.50 | 211 | 2.97–3.16 | 225 | – | – | 12 |
| Ti | 3 1 |
2.88 2.85 |
245 209 |
2.83–2.95 2.81–2.98 |
251 253 |
2.11 1.75 |
0.0 1.9 |
27 |
| V | 4 2 |
2.74 2.75 |
259 260 |
2.74 2.89 |
250 255 |
3.74 3.59 |
0.0 5.1 |
26 |
| Cr | 5 3 |
2.76 2.76 |
252 244 |
2.73–2.86 2.74–2.80 |
244 246 |
4.78 4.68 |
0.0 2.1 |
20 |
| Mn | 6 4 |
2.75 2.65 |
254 260 |
2.66–2.78 2.66–2.76 |
245 253 |
4.63 4.38 |
3.8 0.0 |
44 |
| Fe | 5 3 |
2.52 2.52 |
296 292 |
2.57–2.65 2.56–2.68 |
277 281 |
2.98 2.81 |
5.5 0.0 |
42 |
| Co | 4 2 |
2.42 2.39 |
318 326 |
2.49–2.58 2.49–2.61 |
287 289 |
1.39 1.07 |
9.6 0.0 |
67 |
| Ni | 3 1 |
2.40 2.36 |
318 334 |
2.46–2.54 2.46–2.58 |
285 283 |
0.21 – |
8.1 0.0 |
– – |
| Cu | 2 | 2.46 | 293 | 2.50–2.65 | 262 | 0.25 | – | 38 |
| Zn | 1 | 2.69 | 259 | 2.60–2.78 | 243 | – | – | ~0 |
a Частоты ν(L–Mg(c) и ν(L–Mg(t)) относятся к радиальным и тангенциальным колебаниям допанта L (вдоль связи с центральным атомом Mg(5) и в плоскости поверхностных атомов Mg(1), Mg(2), Mg(10), Mg(15) и Mg(17) соответственно. Из-за смешанного характера колебаний отнесение частот имеет приближенный характер. M – мультиплетность (M = 2S+1)). b Спиновая плотность на атоме допанта ρs(L) выражена в долях е. c D(L) отвечают энергиям распада Mg17L(M) = Mg17(синглет) + L(M) при сохранении суммарной мультиплетности М. Энергии D(L) рассчитывались в более точном приближении с расширенным базисом 6-311 + G*.
Согласно расчетам (табл. 1), у кластеров Mg17L с допантами из первой половины 3d-периода энергетически предпочтительны состояния высокой мультиплетности с двумя, тремя и четырьмя параллельными неспаренными спинами у Ti(↑↑), V(↑↑↑) и Cr(↑↑↑↑). Близлежащие низкоспиновые синглет, дублет и триплет лежат выше них на 2, 5 и 2 ккал/моль соответственно. Напротив, в случае допантов из второй половины периода предпочтительны средне- и низкоспиновые термы Mn(↑↑↑), Fe(↑↑), Co(↑) и нуль-валентное состояние никеля [11], а их высокоспиновые секстет, квинтет, квартет и триплет менее выгодны на 4.0, 5.5, 9.5 и 8.5 ккал/моль соответственно. На полуколичественном уровне рассчитанные спиновые плотности ρ(L) на атомах допантов коррелируют с числом неспаренных спинов, указанных выше в круглых скобках. Подчеркнем, что понижение суммарного спина кластера Mg17L (например, от S до S − 2) оказывается слабо связанным с уменьшением спиновой плотности на атоме допанта (изменения Δρ(L) в большинстве случаев составляют 0.1–0.2 е). Согласно расчетам, оно определяется в основном распариванием электронной пары с образованием двух параллельных спинов, делокализованных на каркасе Mg17 и направленных антипараллельно по отношению к спинам допанта L (антиферромагнитный эффект). Ниже сфокусируемся на наиболее выгодных состояниях: высокоспиновых в случае L = = Ti, V, Cr и среднеспиновых для L = Mn, Fe, Co. У допантов конца 3d-периода (L = Ni и Cu) рассчитанная спиновая плотность ρs(L) не превышает 0.1–0.2е.
Из данных табл. 1 следует, что длины связей допанта R(L–Mg(с)) и R(L–Mg(t)) с центральным и поверхностными атомами магния монотонно уменьшаются при изменении L вдоль периода от Ti до Co в интервале ~0.40 Å симбатно уменьшению атомного радиуса допанта. Соответственно, частоты их валентных колебаний столь же монотонно возрастают в интервалах ~212–328 см–1 у ν(L−Mg(с)) и ~251–289 см–1 у ν(L–Mg(t)). Из табл. 1 следует, что энергия связи допантов D(L) минимальна для L из первой половины периода (~20–27 ккал/моль), увеличивается в его середине, проходя через максимум у кобальта (~66 ккал/моль) и уменьшается к концу периода до ~38 ккал/моль у меди. Энергия присоединение атома цинка к Mg17 очень мала.
Потенциальные поверхности реакций гидрирования кластеров Mg17L
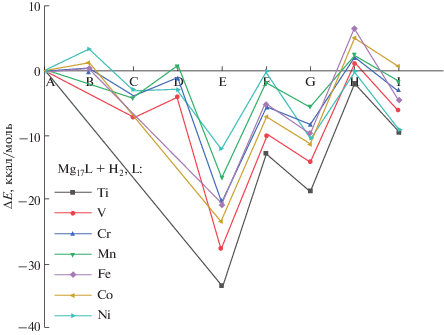
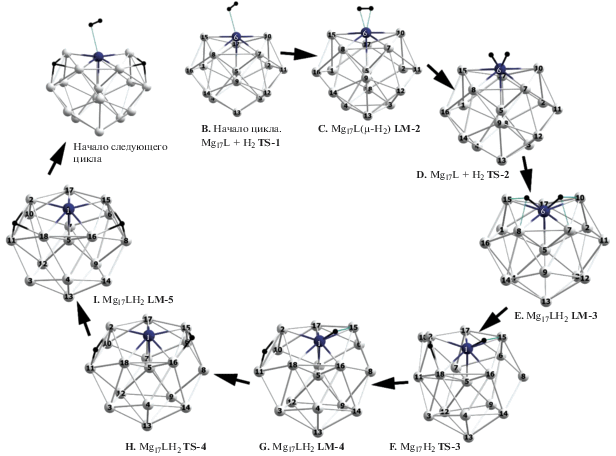
Как было показано ранее [11], каталитический цикл (рис. 2) можно условно разбить на две части: начальную (сорбционную), приводящую к образованию дигидрида Mg17LH2(Е), и заключительную, связанную с “очисткой” допанта (dopant cleaning) и регенерацией его каталитической активности для начала следующего цикла. Как отмечалось ранее [11], стадия сорбции сопровождается значительным выигрышем энергии благодаря образованию в дигидриде Е прочных трех- и четырехцентровых мостиков (L–H–Mg и L–H–2Mg) с атомами Н над ребрами или гранями, включающими допант L. На эндотермической стадии “очистки” оба атома Н удаляются от допанта и в интермедиатах G и I смещаются в мостиковые позиции Mg–H–Mg или Mg–H–2Mg над ближайшими ребрами и гранями, не содержащими допанта.
Рис. 2.
Оптимизированные структуры интермедиатов в реакции (2а) каталитического цикла гидрирования допированных кластеров Mg17L.
В циклах (2), рассчитанных в работе [11], основной терм сохранялся синглетным, а допант Ni оставался в нуль-валентном состоянии на всех стадиях МЭП от А до I. Расчеты аналогичных циклов (2а) с допантами, имеющими незаполненную 3d-оболочку, представляют более сложную проблему из-за появления групп низколежащих термов с разными мультиплетностями и распределением спиновой плотности внутри 3d-оболочки и между допантом L и каркасом Mg17. Проявления эффектов одновременного участия и “пересечения” таких термов на разных участках МЭП могут быть различными. Для количественного описания молекулярных диаграмм подобных систем необходимо использовать многодетерминантные подходы с полными базисными наборами, что выходит за пределы наших вычислительных возможностей. Наши BP86/6-31G*-расчеты не претендуют на высокую точность и фокусируются не столько на абсолютных величинах энергий и барьеров, сколько на их относительных изменениях и тенденциях поведения вдоль МЭП реакций (2а). Основное внимание уделяется участкам ППЭ в окрестности ключевых структур A–I, для которых выполнены расчеты термов с разными значениями мультиплетности М.
На рис. 3 изображены оптимизированные структуры наиболее интересных локальных минимумов и переходных состояний цикла (2а). Более полный набор рассмотренных структур приведен на рис. 1S. В табл. 2 дана сводка рассчитанных свойств особых точек ППЭ для дигидрида Mg17LH2(Е). Структурные и колебательные характеристики изомера I с “очищенным” допантом приведены в табл. 2S. На рис. 4 приведены энергетические диаграммы реакций (2а) с допантами элементов переходного 3d-периода.
Рис. 3.
Оптимизированные структуры локальных минимумов и переходных состояний цикла (2а) Mg17L + H2.
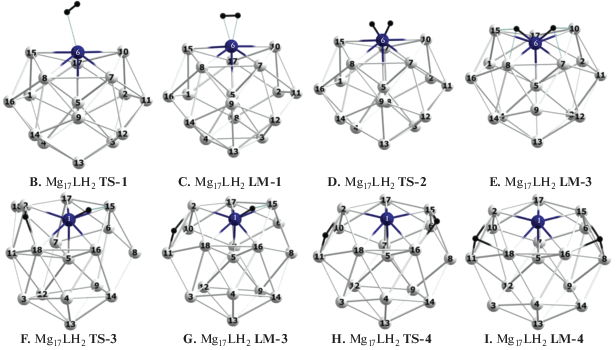
Таблица 2.
Рассчитанные характеристики дигидридного интермедиата Mg17LH2 (E)
| Mg17LH2 (M) | R, Å (L–H) |
φ , град (HLH) |
ν, см–1 (L–H) |
ρs(L) | Z*(H) | ΔE, ккал/моль (M-2/M ) |
D, ккал/моль (H2) |
|---|---|---|---|---|---|---|---|
| Mg17 (3) | – | – | – | 0.54 | – | 4.9 | – |
| (1) | – | – | – | – | – | 0 | – |
| Mg18H2 (3) | 1.91 | 126 | 1275 | 0.37 | –0.13 | 3.8 | |
| (1) | 1.91 | 121 | 1250 | – | –0.13 | 0 | 5 |
| Mg17TiH2 (3) | 1.87 | 117 | 1200 | 1.70 | –0.15 | 0 | 33 |
| (1) | 1.84 | 111 | 1285 | – | –0.14 | 2.6 | |
| Mg17VH2 (4) | 1.81 | 101 | 1254 | 3.22 | –0.13 | 0 | 27 |
| (2) | 1.79 | 80 | 1298 | 2.92 | –0.13 | 2.7 | |
| Mg17CrH2 (5) | 1.76 | 103 | 1270 | 4.28 | –0.11 | 0 | 20 |
| (3) | 1.74 | 87 | 1335 | 3.94 | –0.11 | 1.2 | |
| Mg17MnH2(6) | 1.73 | 116 | 1259 | 4.32 | –0.13 | 0 | 16 |
| (4) | 1.71 | 118 | 1354 | 3.71 | –0.16 | 0.1 | 16 |
| Mg17FeH2 (5) | 1.60 | 79 | 1535 | 1.52 | –0.11 | 6.3 | |
| (3) | 1.60 | 81 | 1525 | 2.21 | –0.10 | 0 | 20 |
| Mg17CoH2 (4) | 1.56 | 85 | 1570 | 0.56 | –0.08 | 5.9 | |
| (2) | 1.57 | 86 | 1580 | 0.29 | –0.08 | 0 | 22 |
| Mg17NiH2 (3) | 1.57 | 95 | 1481 | 0.18 | –0.08 | 4.2 | |
| (1) | 1.57 | 92 | 1515 | – | –0.07 | 0 | 12 |
Расчеты в приближении BP86/6-31G*. Параметры R, φ и ν выражены в ангстремах, градусах и см–1 соответственно, а спиновая плотность на атоме допанта ρs(L) и эффективный заряд Z*(H) на атомах Н – в долях е. M – мультиплетность термов. Энергии ΔΕ(M-2/M) характеризуют относительные стабильности высоко- и низкоспиновых термов. D(H2) – энергия отрыва молекулы Н2 в реакции Mg17LH2(М) → Mg17L(М) + Н2 с сохранением мультиплетности.
Стадия сорбции
В структуре С интермедиата Mg17L(μ-Н2) (рис. 3) активированная молекула водорода характеризуется удлиненным расстоянием R(HH) и низкой частотой валентного колебания ν(HH). У первичного дигидрида Mg17LН2(Е) взаимное положение атомов Н в трех- или четырехцентровых мостиках, включающих атом допанта, зависит от положения допанта в 3d-периоде. В случае L = Ti, V и Cr оба атома Н занимают позиции L–Hb–Mg над смежными ребрами, при L = Fe, Co и Ni предпочтительны позиции L–Hb–2Mg над гранями, а у марганцевого кластера Mg17MnН2 один атом Н образует трехцентровый, а второй – четырехцентровый мостики. Структуры В и D соответствуют переходным состояниям между бесконечно удаленными реагентами и μ-Н2 комплексом С и между μ-Н2 комплексом и дигидридом Е соответственно.
Из табл. 2 видно, что в дигидриде Mg17LН2(Е) при увеличении порядкового номера атома L связи R(LH) укорачиваются от 1.91 до 1.67 Å, частота ν(LH) возрастает от 1275 до 1580 см–1, угол φ(HLH) сокращается на ~30°−40°, а отрицательный эффективный заряд Z(H) на атоме водорода также уменьшается почти вдвое. Уместно заметить, что подобные качественные тенденции найдены нами в аналогичных расчетах изолированных молекул LH2 c теми мультиплетностями, что и у Mg17LН2. Количественное влияние магниевого каркаса на фрагмент LH2 отчетливее всего проявляется в удлинении и ослаблении связей L–H и в уменьшении их полярности. По сравнению с характеристиками свободных молекул LH2 данные, приведенные в табл. 2, для расстояния R(LH) систематически завышены на ~0.10–0.14 Å, а для частоты ν(LH), угла φ(HLH) и заряда Z(H) занижены на ~300–450 см–1, ~15°–20° и ~0.10 е соответственно.
Расчеты термов с разными мультиплетностями свидетельствуют о том, что, как и у кластеров Mg17L, высоко- и низкоспиновые состояния у всех дигидридов Mg17LН2(Е) лежат в интервале ~6–8 ккал/моль, причем в начале 3d-периода предпочтительны высокоспиновые, а в конце периода – низкоспиновые термы. Как и у Mg17L, уменьшение мультиплетности кластера Mg17LН2 на две единицы связано в основном с образованием двух спинов на каркасе Mg17, которые направлены антипараллельно спинам допанта.
В отличие от гомоядерного кластера Mg18, у которого энергия Е(Н2) присоединения молекулы Н2 составляет несколько ккал/моль, у допированных аналогов эта величина возрастает до ~33 ккал/моль (Mg17TiН2), а при увеличении порядкового номера L экзотермичность сорбционной стадии монотонно уменьшается до ~16–20 ккал/моль в середине и ~12 ккал/моль в конце периода.
Между разделенными реагентами А и дигидридом Е на ППЭ реакции (2а) с четырьмя допантами L = V, Cr, Mn, Fe был локализован промежуточный интермедиат Mg17L(μ-Н2)(С), которому отвечает небольшая потенциальная яма, отделенная от А и Е невысокими барьерами В и D порядка нескольких ккал/моль. У кластеров с остальными допантами обнаружить аналогичный μ-Н2-комплекс не удалось. Из рис. 4 видно, что на начальном участке А–В–С изменения энергии невелики и что сорбционная стадия реакций (2a), как правило, может протекать без существенных препятствий.
Стадия “очистки” допанта
Как отмечалось в работе [11], в структуре изомера I кластера Mg17NiH2, локализованной в рамках метода внутренней координаты (irc), очищенный атом Ni смещен во внутреннюю полость и стерически экранирован поверхностными атомами Mg. Для восстановления его каталитической активности необходима дополнительная перегруппировка (“промотирование допанта”) со смещением атома Ni на поверхностную позицию, которая требует дополнительных затрат энергии. У остальных кластеров Mg17LH2 с L = Ti – Co в структуре изомера I, также локализованной в рамках метода irc, очищенный атом допанта L остается в открытой позиции на поверхности каркаса и готов к началу следующего цикла с присоединением новой молекулы Н2 без дополнительного промотирования.
Согласно расчетам (табл. 2S, 3S ), геометрические и колебательные характеристики мостиков Mg–Hb–Mg и Mg–Hb–2Mg с позициями атомов Н над ребрами и гранями магниевого каркаса, удаленными от атома L, сравнительно слабо зависят от природы допанта. Например, у интермедиата I длина связи R(Mg–Hb) и угол φ(MgHbMg) в трехцентровых мостиках Mg–Hb–Mg варьируют в пределах ~1.90–1.92 Å и ~97°–103° для всех атомов L(3d). Колебательные частоты обнаруживают тенденцию к возрастанию с увеличением порядкового номера L в интервалах ~840–1000 и ~1010–1060 см–1 для колебаний атома Нb вдоль и перпендикулярно направлению ребра Mg–Mg. По сравнению с трехцентровыми мостиками у четырехцентровых аналогов Mg–Hb–2Mg расстояния R(Mg–Hb) систематически удлиняются на ~0.10–0.20 Å, а между собой они могут отличаться в пределах ~0.10–0.15 Å. Колебания мостиковых атомов Н в ИК-спектрах, как правило, характеризуются высокой интенсивностью.
Из энергетических диаграмм (рис. 4) видно, что при удалении атомов Н от допанта и переходе от дигидрида Е в “полуочищенный” и далее в “полностью очищенный” интермедиаты G и I рассчитанная энергия ΔE(E → G), необходимая для перемещение первого атома Н, минимальна при L = Ni (~2 ккал/моль), а с уменьшением порядкового номера L увеличивается до ~8−10 ккал/моль в середине и ~15 ккал/моль в начале периода. Барьер F, разделяющий интермедиаты E и G и отсчитанный от Е, возрастает в еще более широких пределах: от ~12 ккал/моль при L = Ni до ~27–33 ккал/моль у L = Ti и V. Энергии ΔE(G → I) перемещения второго атома Н сопоставимы с ΔE(E → G) и лежат тесной группой в интервале ~7–10 ккал/моль для всех допантов из 3d-периода, а барьер Н на этом пути, отсчитанный от G, почти в полтора раза ниже первого барьера F. Суммарные энергии цикла ΔE(А → I), оцененные по разности полных энергий бесконечно удаленных реагентов А и очищенного интермедиата I, также не превышают ~6–9 ккал/моль. При дальнейших перемещениях атомов Н на еще более удаленные ребра и грани значения этих энергий должны сближаться и уменьшаться до нескольких ккал/моль, а соответствующие участки диаграммы должны приближаться к диаграмме, отвечающей поверхностной миграции атомов Н вокруг гомоядерного кластера Mg18.
Анализ диаграмм на рис. 4 свидетельствует о том, что “очистка” допанта является лимитирующей стадией каталитического цикла (2а) для всех рассмотренных допантов из 3d-периода, и что более высокий барьер связан с перемещением первого атома водорода. У допантов начала периода (L = Ti и V) этот барьер трудно преодолим, но и в наиболее благоприятном случае (с допантом из конца периода, L = Ni) он остается весьма ощутимым кинетическим препятствием, которое может быть преодолено только в условиях повышенных температур. Согласно расчетам, каталитическая активность допанта должна падать с уменьшением порядкового номера атома L(3d).
Из-за локального характера активного реакционного центра, включающего атомы Н, допант и ближайшие соседние атомы Mg, можно полагать, что барьеры высотой ~12–15 ккал/моль и более на стадии “очистки” допанта останутся значительными и для более крупных магниевых частиц, где они также будут служить ощутимым кинетическим препятствием. Заметим, что на качественном уровне этот вывод созвучен с фактом, что измеренные температуры гидрирования магния с использованием катализаторов и повышенного давления к настоящему времени не опускаются ниже 300–350°С, и процессы идут недостаточно быстро. Разумеется, подобные сопоставления носят предварительный характер. Настоящие расчеты ограничены начальной стадией реакций (2) и (2а), и другие барьеры, отвечающие следующим стадиям гидрирования, например внутренней миграции атомов Н через поверхностный гидридный слой и др., подробно ранее описанным для алюминиевых кластеров [27], остаются вне поля рассмотрения. Эти сложные вопросы требуют дальнейших исследований.
В заключение уместно сказать несколько слов о сравнении результатов настоящих расчетов реакций (2а) с результатами предыдущих DFT-расчетов [12, 13] родственных реакций гидрирования алюминиевых кластеров:
(3)
${\text{A}}{{{\text{l}}}_{{{\text{12}}}}}{\text{L}} + {{{\text{H}}}_{2}} \to {\text{A}}{{{\text{l}}}_{{{\text{12}}}}}{\text{L}}{{{\text{H}}}_{2}}$Список литературы
Yartys V.A., Lototskyy M.V., Akiba E. et al. // Int. J. Hydrogen Energy. 2018. V. 44. P. 7809. https://doi.org/10.1016/j.ijhydene.2018.12.212
Tarasov B.P., Arbuzov A.A., Mozhzhuhin S.A. et al. // Int. J. Hydrogen Energy. 2019. V. 44. P. 29212. https://doi.org/10.1016/j.ijhydene.2019.02.033
Sun Y., Shen C., Lai Q. et al. // Energy Storage Materials. 2017. V. 10. P. 168 https://doi.org/10.1016/j.ensm.2017.01.010
Son V.B., Tarasov B.P. // Russ. J. Inorg. Chem. 2020. V. 65. P. 147. https://doi.org/10.1134/S0036023620020199
Wang X., Andrews L. // J. Phys. Chem. A. 2004. V. 108. P. 11511. https://doi.org/10.1021/jp046410h
Luo Z., Grover C.J., Reber A.C. et al. // J. Am. Chem. Soc. 2013. V. 135. P. 4307. https://doi.org/10.1021/ja310467n
Grover C.J., Reber A.C., Khanna S.N. // J. Chem. Phys. 2017. V. 146. P. 2 243 301. https://doi.org/10.1063/1.4985093
Lu B.-J., Li X.-T., Zhao Y.-J. et al. // Aip Advances. 2017. V. 7. P. 095023. https://doi.org/10.1063/1.5000792
Janecek S., Krotscheck E., Liebrecht M., Wahl R. // Eur. Phys. J. 2011. V. 63. P. 377 https://doi.org/10.1140/epjd/e2011-10694-2
Xia X., Kuang X., Lu C. et al. // J. Phys. Chem. A. 2016. https://doi.org/10.1021/acs.jpca.6b07322
Maltsev A.P., Charkin O.P. // Russ. J. Inorg. Chem. 2020. V. 65. № 2. P. 188. https://doi.org/10.31857/S0044457X20020117
Mikhailin A.A., Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2013. V. 58. № 12. P. 1439. https://doi.org/10.1134/S0036023613120073
Mikhailin A.A., Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2016. V. 61. № 12. P. 1558. https://doi.org/10.1134/S0036023616120135
Guo L. // J. Phys. Chem. 2013. V. 117. № 16. P. 3458. https://doi.org/10.1021/jp310833y
Varano A., Henry D.J., Yarovsky I. // J. Phys. Chem. C. 2014. V. 118. P. 19865.
Vanbuel J., Fernandes E.M., Ferrary P. et al. // Chem. Eur. J. 2017. V. 23. P. 15638. https://doi.org/10.1002/chem.201704361
Vanbuel J., Jia M.-Y., Ferrary P. et al. // Top. Catal. 2018. V. 61. P. 62. https://doi.org/10.1007/s11244-017-0878-x
Jia M.-Y., Vanbuel J., Ferrary V. et al. // J. Phys. Chem. 2018. V. 122. P. 18247. https://doi.org/10.1021/acs.jpcc.8b04332
Mikhailin A.A., Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2015. V. 60. № 10. P. 1238. https://doi.org/10.1134/S0036023615100137
Trivedi R., Bandyopadhyay D. // Int. J. Hydrogen Energy. 2015. V. 40. № 37. P. 12 727. https://doi.org/10.1016/j.ijhydene.2015.07.122
Trivedi R., Bandyopadhyay D. // Int. J. Hydrogen Energy. 2016. V. 41. № 44. P. 20113. https://doi.org/10.1016/j.ijhydene.2016.09.007
Um K.-J., Wi J.-H., Hong S.-I. et al. // Int. J. Hydrogen Energy. 2019. V. 44. № 16. P. 8252. https://doi.org/10.1016/j.ijhydene.2019.01.192
Bahou S., Labrim H., Lakhal M. et al. // Int. J. Hydrogen Energy. 2020. V. 45. № 18. P. 10806. https://doi.org/10.1016/j.ijhydene.2020.02.024
Kurko S., Paskaš Mamula B., Rmuš J. et al. // Int. J. Hydrogen Energy. 2020. V. 45. № 14. P. 7947. https://doi.org/10.1016/j.ijhydene.2019.05.015
Frisch M.J., Trucks G.W., Schlegelet H.B. et al. Gaussian 09. Revision A.02 Gaussian, Inc., Wallingford CT, 2013.
Becke A.D. // J. Phys. Chem. 1993. V. 98. P. 5648.
Charkin O.P., Klimenko N.M., Charkin D.O. // Chem. Phys. 2019. V. 522. P. 112. https://doi.org/10.10167/j.champhys.2019.02.007
Дополнительные материалы
- скачать EMS_1.docx
- Рис. 1S. - Рис. 2S.
Таблица 1S. - Таблица 2S.
Инструменты
Журнал неорганической химии