1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 68, № 11, 2023

Журнал неорганической химии, 2023, T. 68, № 11, стр. 1637-1655

Синтез, термодинамические свойства и ионная проводимость соединений на основе ниобатов висмута, замещенных редкоземельными элементами (обзор)

Н. И. Мацкевич a, *, А. Н. Семерикова a, Д. А. Самошкин a, b, С. В. Станкус b, В. П. Зайцев a, c, В. А. Кузнецов a, А. Ю. Новиков a

a Институт неорганической химии им. А.В. Николаева СО РАН
630090 Новосибирск, пр-т Академика Лаврентьева, 3, Россия

b Институт теплофизики им. С.С. Кутателадзе СО РАН
630090 Новосибирск, пр-т Академика Лаврентьева, 1, Россия

c Сибирский государственный университет водного транспорта
630099 Новосибирск, ул. Щетинкина, 33, Россия

* E-mail: nata.matskevich@yandex.ru

Поступила в редакцию 02.05.2023
После доработки 10.08.2023
Принята к публикации 10.08.2023

Полный текст (PDF)

Аннотация

Представлены методы синтеза, термодинамические и функциональные свойства соединений на основе ниобатов висмута, замещенных редкоземельными элементами. Данные соединения являются перспективными материалами для топливных элементов, керамических кислородных генераторов, электрокатализа и др. Как показал обзор, большинство соединений имеют кубическую структуру δ-формы оксида висмута, которая обладает самой высокой ионной проводимостью среди твердотельных ионных проводников. Соединения обладают высокой энтальпией решетки и поэтому являются перспективными высокоэнергетическими соединениями. В обзоре рассмотрены работы по базовым термодинамическим характеристикам ниобатов висмута, замещенных редкоземельными элементами. Проанализировано изменение стандартных энтальпий образования, энтальпий решеток, теплоемкости при замене одного редкоземельного элемента другим. Показано, что с уменьшением радиуса РЗЭ стандартные энтальпии образования и энтальпии решеток увеличиваются. Изучено изменение ионной проводимости при изменении температуры и содержания редкоземельного элемента. Показано, что с увеличением температуры и содержания РЗЭ проводимость увеличивается.

Ключевые слова: оксид висмута, оксид ниобия, редкоземельные элементы, синтез, структура, энтальпия образования, энтальпия решетки, теплоемкость

ВВЕДЕНИЕ

Известно, что δ-форма оксида висмута (δ-Bi2O3) обладает уникальными свойствами: она имеет кубическую структуру и наиболее высокую ионную проводимость среди твердотельных ионных проводников [1–5]. Эти уникальные свойства открывают перспективы для использования соединений со структурой δ-формы оксида висмута в качестве электролитов топливных элементов, керамических кислородных генераторов и др. Получить кубическую структуру очень важно для применения, поскольку в этом случае функциональные свойства мало зависят от направления. Однако проблема заключается в том, что δ-форма оксида висмута является устойчивой в очень узком интервале температур – от 1003 до 1103 K.

Для увеличения интервала устойчивости δ-формы оксида висмута используют замещение висмута различными элементами III–VII групп. Висмут замещают на такие элементы, как ниобий, вольфрам, рений, а также редкоземельные металлы [6–10]. В ряде случаев применяют содопирование, т.е. замещение двумя и более элементами. Для перспективного применения необходимо соблюдение по меньшей мере двух условий: соединения должны быть устойчивыми и обладать высокими функциональными характеристиками.

Очень хорошие результаты были достигнуты при содопировании оксида висмута рением(VII) и редкоземельными элементами (РЗЭ) [11–15]. Был получен новый класс соединений состава Bi12.5RE1.5ReO24.5 (RE – редкоземельный элемент). Данные соединения имеют кубическую структуру флюорита (пр. гр. Fm3m). Они обладают высокой ионной проводимостью, сравнимой с проводимостью наиболее используемых соединений на основе оксида висмута BiVMO [16, 17]. Одним из достижений для соединений состава Bi12.5R1.5ReO24.5 является то, что удалось получить чистые фазы для всех РЗЭ от лантана до лютеция. Однако рений является дорогостоящим элементом. Кроме того, полученные перренаты висмута являются гигроскопичными. В связи с этим мировое научное сообщество обратилось к поиску новых содопированных соединений на основе оксида висмута. Одними из таких соединений оказались ниобаты висмута, замещенные редкоземельными элементами. Среди большого выбора катионов для замещения δ-формы оксида висмута Nb5+ является наиболее предпочтительным из-за его высокой эффективности стабилизировать кубическую δ-форму оксида висмута до комнатной температуры. Минимальная концентрация ниобия, необходимая для стабилизации δ-формы оксида висмута, составляет 10%.

В настоящем обзоре с акцентом на термодинамические свойства приведены методы синтеза, базовые термодинамические характеристики и некоторые функциональные свойства ниобатов висмута и ниобатов висмута, замещенных редкоземельными элементами. Кроме того, проанализированы закономерности изменения термодинамических свойств в зависимости от радиуса РЗЭ. Термодинамические исследования позволяют оптимизировать условия синтеза соединений, определить изменения параметров, характеризующих стабильность и деградацию материалов и др.

СИНТЕЗ СОЕДИНЕНИЙ

Нами рассмотрен синтез ниобатов висмута и ниобатов висмута, замещенных редкоземельными элементами. Одной из целей было описание способов получения веществ со структурой δ-формы оксида висмута, которая обладает наиболее высокой ионной проводимостью. Как показало изучение литературы, основным методом синтеза ниобатов висмута является метод твердофазных реакций. Твердофазный синтез проводится при высоких температурах из оксида висмута и оксида ниобия (Nb2O5). Ниже приведем некоторые из работ, в которых были получены ниобаты висмута различного состава.

В работе [18] методом твердофазного синтеза был получен поликристаллический образец Bi3NbO7 из стехиометрической смеси высокочистых Bi2O3 и Nb2O5. После тщательного перемешивания порошок сначала нагревали при 973 K для образования менее летучих соединений ниобия и во избежание потерь Bi2O3 в процессе спекания при более высокой температуре, а затем прореагировавший порошок прокаливали при 1073 K для получения Bi3NbO7.

Оригинальный метод получения нанопластин ниобата висмута (Bi3NbO7) был предложен в работе [19]. Для синтеза использовали цитрат висмута (BiC6H5O7), пятиокись ниобия (Nb2O5), раствор аммиака (NH3 · H2O), NaOH и этанол. Сверхструктуры нанопластин ниобата висмута были синтезированы одностадийным гидротермальным методом с использованием BiC6H5O7 и Nb2O5 в качестве прекурсоров. Сначала к цитрату висмута добавляли аммиак. Затем в раствор NaOH добавляли Nb2O5 при магнитном перемешивании. Далее раствор, содержащий BiC6H5O7, приливали к суспензии Nb2O5. Полученную суспензию переносили в автоклав. Смесь нагревали в автоклаве при 473 K под автогенным давлением, а затем охлаждали на воздухе до комнатной температуры. Образовавшиеся осадки тщательно промывали этанолом и деионизированной водой и сушили при 323 K на воздухе.

В работе [20] кристаллы BiNbO4 были получены обжигом смеси полуторного оксида висмута высокой чистоты и оксида ниобия(V). Вещества помещали в платиновую капсулу и выдерживали при температуре 388 K на воздухе. Кристаллы представляли собой бледно-желтые призмы.

В работе [21] был синтезирован керамический образец BiNbO4 методом твердофазных реакций. Начальные реагенты Bi2O3 и Nb2O5 взвешивали в стехиометрических количествах. Синтез проводили по реакции: Bi2O3 + Nb2O5 → 2BiNbO4. Смесь оксидов сначала растирали в агатовой ступке. После этого выполняли мокрый помол с использованием этилового спирта, планетарной мельницы и циркониевых шаров. После измельчения порошки высушивали. Далее порошки прессовали в таблетки диаметром 20 мм под давлением 300 МПа в матрице из нержавеющей стали. После этого спрессованные таблетки помещали в тигель из оксида алюминия и обжигали на воздухе при 1023 K. После термообработки таблетки измельчали в ступке и подвергали мокрому измельчению и повторной сушке. Окончательное спекание проводили на воздухе в печи при температурах 1143, 1183, 1323, 1353 K.

Авторы [22] синтезировали соединение BiNbO4 методом твердофазного синтеза из Bi2O3 и Nb2O5. Образцы тщательно перемешивали и отжигали в печи при температуре выше 1273 K. После отжига проводили рентгенофазовый анализ, который показал, что получена индивидуальная фаза.

В работе [23] соединение BiNbO4 было получено методом низкотемпературного синтеза с применением золь-гель технологии. Для синтеза использовали нитрат висмута и нитрат ниобия. Фаза была получена разложением нитратного комплекса при 873 K, что на 200 K ниже температуры твердофазного синтеза.

В работе [24] соединение BiNb5O14 было синтезировано методом твердофазного синтеза из Bi2O3 и Nb2O5. Стехиометрическую смесь перемешивали в агатовой ступке и нагревали в платиновом тигле до температуры 1173 K на воздухе. Далее смесь снова перетирали и нагревали до температуры 1223 K. Рентгенофазовый анализ показал, что фаза является индивидуальной.

В работе [25] соединение Bi5NbO10 было синтезировано золь-гель методом. В качестве основных реактивов использовали нитрат висмута Bi(NO3)3 ⋅ 5H2O и Nb2O5. Для проведения синтеза оксид ниобия растворяли в плавиковой кислоте. Далее гидрат оксида ниобия (Nb2O5 ⋅ nH2O) осаждали, используя раствор аммиака. Нитрат висмута растворяли в этилендиаминтетрауксусной кислоте. После этого растворы, содержащие висмут и ниобий, смешивали и нагревали до 333 K, а затем до 373 K. Последнюю стадию нагрева проводили при температурах 1073–1173 K. Рентгенофазовый анализ подтвердил индивидуальность соединения.

Фаза Bi4NbO8.5 была синтезирована из Bi2O3 и Nb2O5 методом твердофазного синтеза [26]. Стехиометрическую смесь подвергали мокрому помолу и отжигали при температуре 1013 K. После этого смесь отжигали при 1073 K. Индивидуальность соединения подтверждена рентгенофазовым анализом.

Рассмотрение работ по синтезу недопированных ниобатов висмута показало, что для синтеза этих соединений применяют два метода: твердофазный синтез и золь-гель метод. В качестве прекурсоров используются оксид висмута, оксид ниобия(V), цитрат висмута, нитрат висмута, нитрат ниобия. Для подготовки смеси используется как сухой, так и мокрый помол. Соединения синтезируют как в виде таблеток, так и в виде порошка. Золь-гель метод снижает температуру синтеза на 200 K.

Далее перейдем к описанию синтеза ниобатов висмута, замещенных редкоземельными элементами. Несколько работ посвящено замещению ниобатов висмута иттрием.

Авторы [27–29] синтезировали образцы Bi3Nb1– xYxO7– x (0.0 ≤ x ≤ 1.0) методом твердофазного синтеза с использованием соответствующих количеств Bi2O3, Y2O3 и Nb2O5. Изначально смесь измельчали в этаноле с помощью планетарной шаровой мельницы. Высушенную смесь нагревали при температуре 1013 K, затем охлаждали, перемалывали и прессовали. Прессование проводили при давлении 400 МПа, затем смесь выдерживали при температуре 1073 K. Авторы [30, 31] синтезировали ниобат висмута, замещенный иттрием, Bi3.5Nb1 –xYxO7.75 –x (0.0 < x < 0.8) и соединение Bi4NbO8.5 [30], а также фазу Bi7Nb2 – 2xY2xO15.5 – 2x [31] по технологии, описанной в работах [27–29].

В работе [32] синтезировали ниобат висмута, замещенный иттербием, состава Bi3Nb1 –xYbxO7 –x (0.2 < x < 0.8) из высокочистых оксидов висмута, ниобия и иттербия. Прекурсоры перемешивали в планетарной мельнице в этаноле, затем нагревали при температурах 1023, 1123 и 1223 K.

Авторы [33] по керамической технологии синтезировали ниобат висмута, замещенный эрбием Bi3Nb1 –xErxO7 –x (x = 0.2; 0.4; 0.6; 0.8), из высокочистых оксидов. Сначала вещества перемалывали в планетарной мельнице, затем нагревали при температурах 1023 и 1073 K.

Серию соединений на основе ниобатов висмута, замещенных редкоземельными элементами, синтезировали авторы работ [34–38]. В работе [34] из оксидов методом твердофазного синтеза были получены соединения Bi3 –xYxNb1 –yWyO7 ± δ (x = 0.05; 0.1; y = 0–03). Синтез проводили при температурах 873–1123 K. Соединение Bi6.95Y0.05Nb2O15.5 было получено методом твердофазного синтеза по керамической технологии при температуре 1093 K в работе [35]. Тем же самым методом в работах [36–38] синтезированы соединения Bi3Nb1 –xErxO7 – δ, Bi2.95Y0.05Nb1 –yZryO7 ± δ (y = 0–0.5), Bi6.95Y0.05Nb2 –yZryO15.5 ± δ (y = 0.1–1).

В работах [39–43] была получена серия соединений на основе ниобата висмута, замещенного редкоземельными элементами (Lu, Dy, Er, Sm) состава Bi3Nb0.2RE0.8O6.2 (RE – редкоземельный элемент). Соединения Bi3Nb0.2RE0.8O6.2 (RE = Lu, Er, Dy, Sm) были синтезированы методом твердофазного синтеза из стехиометрических смесей оксидов: Bi2O3, Lu2O3, Er2O3, Dy2O3, Nb2O5, Sm2O3. Высокочистый оксид висмута марки 5 N (99.999 мас. %) подвергался глубокой очистке в ИНХ СО РАН. Содержание примесей Cu, Fe, K, Mg, Mn, Na, Ni, Pb, Sb, Si, Te, Zn, определенное методом масс-спектрометрии с индукционной плазмой (масс-спектрометр iCAP-Qc), не превышало 10–5 мас. %. Стехиометрические смеси перемешивались в планетарной мельнице Fritsch Pulverisette 6. После перемешивания смесь спрессовывалась (пресс ПГР-400) и отжигалась в печи (SNOL 4/1300). Наилучшие результаты по синтезу были достигнуты при температуре 1073 K.

Характеризация образцов Bi3Nb0.2RE0.8O6.2 (RE = = Lu, Er, Dy, Sm), полученных в работах [39–43], была выполнена рентгенофазовым и химическим анализами. Содержание элементов определили методом атомно-абсорбционной спектроскопии, содержание кислорода – методом восстановительного плавления. Результаты анализов показали, что в пределах погрешности полученные соединения соответствуют формулам: Bi3Nb0.2RE0.8O6.2 (RE = = Lu, Er, Dy, Sm).

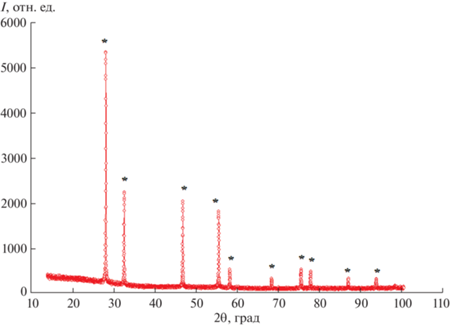
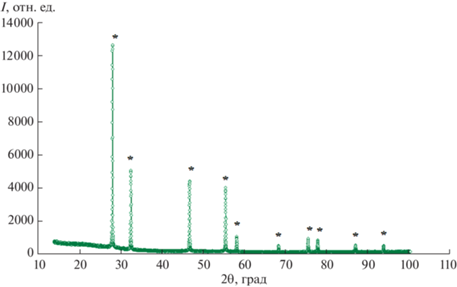
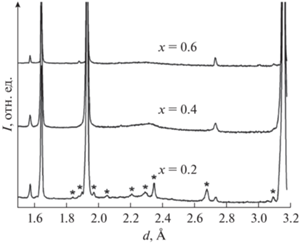
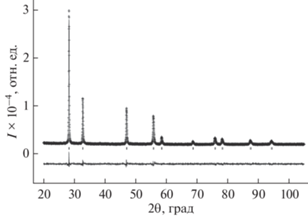
Рентгенофазовый анализ полученных образцов проводили на дифрактометре Shimadzu XRD-7000 (CuKα-излучение). Типичные дифрактограммы образцов, принадлежащих к пр. гр. Fm3m, приведены на рис. 1, 2.

Рис. 1.

Типичная дифрактограмма образца Bi3Nb0.2Dy0.8O6.2, звездочкой обозначены пики, принадлежащие соединению Bi3Nb0.2Dy0.8O6.2. Данные работ [39–43].

Рис. 2.

Типичная дифрактограмма образца Bi3Nb0.2Lu0.8O6.2, звездочкой обозначены пики, принадлежащие соединению Bi3Nb0.2Lu0.8O6.2. Данные работ [39–43].

С использованием программы FullProf в работах [39–43] определена пространственная группа и параметры решетки для соединений Bi3Nb0.2RE0.8O6.2. Пр. гр. Fm3m (флюорит, кубическая). Параметр решетки для Bi3Nb0.2Sm0.8O6.2: a = = 0.54894(8) нм. Параметр решетки Bi3Nb0.2Dy0.8O6.2: a = 0.54853(9) нм. Параметр решетки для Bi3Lu0.8Nb0.2O6.2: а = 0.54814(7) нм.

Рассмотрение работ по синтезу ниобатов висмута, замещенных редкоземельными элементами, показало, что проводилось замещение ниобия на иттрий, иттербий, эрбий, лютеций, диспрозий, самарий. В качестве прекурсоров использовались: оксид висмута, оксиды РЗЭ, оксид ниобия(V). Для синтеза замещенных ниобатов висмута применялся только метод твердофазного синтеза. В то время как для синтеза незамещенных ниобатов висмута использовалось два метода: твердофазных реакций и золь-гель. Для подготовки смеси использовался как мокрый помол в этаноле, так и сухой помол.

ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА СОЕДИНЕНИЙ

Основные базовые термодинамические характеристики, которые необходимы для предсказания и оптимизации условий синтеза, установления параметров изменения стабильности и деградации материалов, определения характеристик реакций взаимодействия с окружающей средой (вода, воздух, углекислый газ и др.), определения существования и параметров фазовых переходов и др. – это стандартные энтальпии образования, энтальпии решеток, энтропия, теплоемкость.

Для определения стандартных энтальпий образования сложных соединений, в основном, используются два метода: метод калориметрии растворения [44–48] и метод высокотемпературной калориметрии в расплавах [49, 50]. В редких случаях используется метод калориметрии сжигания. Метод калориметрии растворения заключается в создании термохимического цикла таким образом, что энтальпия растворения исследуемого вещества при комнатных температурах в растворах кислот или щелочей сравнивается с энтальпиями растворения прекурсоров, содержащих входящие в соединения элементы. А далее на основе полученных экспериментальных данных рассчитываются стандартные энтальпии образования. В качестве растворителей используются растворы концентрированных или разбавленных кислот и щелочей или подходящие органические жидкости. Метод высокотемпературной реакционной калориметрии заключается в создании подобного термохимического цикла так, что энтальпия растворения исследуемого соединения при высоких температурах в расплавах сравнивается с энтальпиями растворения прекурсоров. В качестве высокотемпературных расплавов используются расплавы молибдатов или вольфраматов или расплавы боратных стекол. В методическом плане при определении стандартных энтальпий образования ниобатов висмута, замещенных редкоземельными элементами, метод калориметрии растворения является наиболее подходящим, чем метод высокотемпературной реакционной калориметрии. Метод растворной калориметрии позволяет получить энтальпии образования при стандартной температуре 298.15 K. В то время как в методе высокотемпературной реакционной калориметрии измеряют энтальпии образования при высоких температурах, а пересчет к стандартной температуре требует знания теплоемкостей.

Для определения высокотемпературной теплоемкости, температур и теплот фазовых переходов, в основном, используется два метода: метод калориметрии смешения и метод дифференциальной сканирующей калориметрии (ДСК) [51–54]. В методе калориметрии смешения (или дроп-калориметрии) проводится сброс исходного вещества из зоны высоких температур в зону комнатных температур, при этом измеряют изменение теплосодержания. Метод является достаточно точным (0.1–0.5%), однако требует больших временных затрат и больших объемов веществ. В методе ДСК исследуемое вещество располагается в специальной ячейке и нагревается до заданных температур с определенной скоростью, при этом измеряется дифференциальный тепловой поток между ячейкой с образцом и пустой ячейкой сравнения. Далее с использованием данных эталонного материала с хорошо изученными свойствами или стандарта (например, Al2O3) рассчитывается теплоемкость исследуемого вещества “методом отношений”. Метод требует малых количеств вещества (порядка 10 мг и более), но значительно уступает методу калориметрии смешения по точности (1–3%). Однако для решения большинства задач использование метода ДСК достаточно.

Поиск по наиболее полной базе термодинамических свойств [55] показал, что термодинамические характеристики соединений в системе Bi2O3–Nb2O5–RE2O3 практически отсутствуют.

Стандартные энтальпии образования

В работе [56] измерена энтальпия образования ниобата висмута состава BiNbO4 из оксидов. Для определения энтальпии образования авторы использовали высокотемпературную калориметрию. Соединения Bi2O3, Nb2O5, BiNbO4 растворялись в расплаве молибдата натрия 3Na2O + 4MoO3 при 1073 K.

Все измерения проводились в высокотемпературном калориметре Multi HTC 96 (Setaram, Франция). Термохимический цикл для определения энтальпии образования из оксидов представлен ниже:

(1a)
$\begin{gathered} 0.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + {\text{расплав }}1 = \\ = {\text{расплав }}2 + 0.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{1a}}}}^{0}, \\ \end{gathered} $
(2a)
$\begin{gathered} 0.5{\text{N}}{{{\text{b}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + {\text{расплав }}2 = \\ = \,\,{\text{расплав }}3 + 0.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{2a}}}}^{0}, \\ \end{gathered} $
(3a)
$\begin{gathered} {\text{BiNb}}{{{\text{O}}}_{{\text{4}}}}\left( {{\text{тв}}} \right) + {\text{расплав }}1 = \\ = \,\,{\text{расплав }}3 + {{\Delta }_{{{\text{sol}}}}}H_{{{\text{3a}}}}^{0}. \\ \end{gathered} $

Суммируя уравнения реакций (1a), (2a) и вычитая уравнения реакции (3a) можно получить уравнение реакции (4a):

(4a)
$\begin{gathered} 0.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 0.5{\text{N}}{{{\text{b}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) = \\ = \,\,{\text{BiNb}}{{{\text{O}}}_{{\text{4}}}}\left( {{\text{тв}}} \right) + {{\Delta }_{{{\text{oх}}}}}{{H}^{0}}. \\ \end{gathered} $

С использованием закона Гесса можно получить:

${{\Delta }_{{{\text{oх}}}}}{{H}^{0}} = 0.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{1a}}}}^{0} + 0.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{2a}}}}^{0} - {{\Delta }_{{{\text{sol}}}}}H_{{{\text{3a}}}}^{0}.$

Полученная энтальпия образования составляла ΔoхH0(BiNbO4, s) = −41.9 ± 11.1 кДж/моль. Величина была получена на основе экспериментально измеренных при температуре 1073 K энтальпий растворения. Величины энтальпий растворения при температуре 1073 K были пересчитаны к стандартной температуре 298.15 K c использованием литературных данных по инкрементам энтальпий. Рассчитанная с использованием данных из справочника [55] стандартная энтальпия образования для соединения BiNbO4 составила: ΔfH0(BiNbO4) = –1279.7 ± 11.5 кДж/моль.

В работах [39–42] были измерены стандартные энтальпии образования ниобатов висмута, замещенных редкоземельными элементами, состава Bi3Nb0.2RE0.8O6.2 (RE = Sm, Er, Dy, Lu). Для определения этих величин был использован метод калориметрии растворения при комнатных температурах. Для этого в работах [39–42] разработали два термохимических цикла. В качестве растворителя был выбран 4 M раствор соляной кислоты. Первый термохимический цикл был разработан для ниобатов висмута, замещенных самарием, диспрозием, эрбием. Цикл для соединений Bi3Nb0.2Sm0.8O6.2, Bi3Nb0.2Dy0.8O6.2, Bi3Nb0.2Er0.8O6.2 заключался в растворении соединений Bi3Nb0.2Sm0.8O6.2, Bi3Nb0.2Dy0.8O6.2, Bi3Nb0.2Er0.8O6.2, а также прекурсоров Bi2O3, Sm2O3, Dy2O3, Er2O3, NbCl5 в 4 M HCl.

Второй термохимический цикл был разработан для соединения Bi3Nb0.2Lu0.8O6.2. Цикл заключался в растворении Bi3Nb0.2Lu0.8O6.2, Bi2O3, NbCl5, Lu в 4 M HCl.

Растворение проводили в автоматизированном калориметре растворения с изотермической оболочкой, который представлял собой сосуд Дьюара, расположенный в латунном стакане [57–59]. С целью проверки правильности работы системы проводили растворение стандартного вещества – хлорида калия [60]. Результаты экспериментов показали, что в пределах погрешностей полученная в работах [39–43] величина энтальпии растворения хлорида калия, равная 17.41 ± ± 0.04 кДж/моль (моляльность 0.028 моль/кг), хорошо согласуется с рекомендованными в литературе значениями: 17.42 ± 0.02 кДж/моль [60], 17.47 ± 0.07 кДж/моль [61].

Первый термохимический цикл для определения стандартной энтальпии образования соединений Bi3Nb0.2RE0.8O6.2 (Sm, Dy, Er), используемый в работах [39–42], в обобщенном виде представлен ниже:

(1b)
$\begin{gathered} 1.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 9{\text{HCl}}\left( {{\text{р - р}}} \right) + {\text{раствор }}1 = \\ = \,\,{\text{3BiC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + 4.5{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}2 + 1.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{1b}}}}^{0}, \\ \end{gathered} $
(2b)
$\begin{gathered} 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + {\text{раствор }}2 = 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}3 + 0.2{{\Delta }_{{{\text{sol}}}}}H_{{{\text{2b}}}}^{0} + \\ \end{gathered} $
(3b)
$\begin{gathered} 0.4{\text{R}}{{{\text{E}}}_{{\text{2}}}}{{{\text{O}}}_{3}}\left( {{\text{тв}}} \right) + 2.4{\text{HCl}}\left( {{\text{р - р}}} \right) + {\text{раствор }}3 = \\ = \,\,0.8{\text{REC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + {\text{1}}{\text{.2}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}4 + 0.4{{\Delta }_{{{\text{sol}}}}}H_{{{\text{3b}}}}^{0}, \\ \end{gathered} $
(4b)
$\begin{gathered} {\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}\left( {{\text{тв}}} \right) + 12.4HCl\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}1 = \,3{\text{BiC}}{{{\text{l}}}_{3}}\left( {{\text{р - р}}} \right) + 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{0}}{\text{.8REC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + \\ + \,\,6.2{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {{\text{р - р}}} \right) + {\text{раствор }}4 + {{\Delta }_{{{\text{sol}}}}}H_{{{\text{4b}}}}^{0}.~ \\ \end{gathered} $

Зная энтальпии растворения реакций (1b)–(4b), можно составить уравнение и рассчитать энтальпию реакции (5b):

(5b)
$\begin{gathered} 1.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + 0.4{\text{R}}{{{\text{E}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + \\ + \,\,0.{\text{5}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {\text{ж}} \right) = {\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}\left( {{\text{тв}}} \right) + \\ + \,\,{\text{HCl}}\left( {{\text{р - р}}} \right) + {{\Delta }_{r}}H_{{{\text{5b}}}}^{0} \\ \end{gathered} $
Здесь Δr$H_{{{\text{5b}}}}^{0}$ = – Δsol$H_{{{\text{4b}}}}^{0}$ + 1.5Δsol$H_{{{\text{1b}}}}^{0}$ + 0.2Δsol$H_{{{\text{2b}}}}^{0}$ + + 0.4Δsol$H_{{{\text{3b}}}}^{0}$.

Далее на основе энтальпии реакции (5b) c использованием данных [39–43] были рассчитаны стандартные энтальпии образования соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er).

Измеренные в работах [39–42] энтальпии растворения приведены ниже. Энтальпия растворения оксида висмута (Bi2O3) в 4 M HCl составляла ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{1b}}}}^{0}$ = –187.68 ± 2.51 кДж/моль, энтальпия растворения хлорида неодима (NbCl5) в 4 M HCl – ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{2b}}}}^{0}$ = –210.05 ± 4.98 кДж/моль. Энтальпия растворения оксида самария в 4 M HCl, необходимая для расчета стандартной энтальпии образования Bi3Nb0.2Sm0.8O6.2, заимствована из работы [62] и составила: ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{3b}}}}^{0}$(Sm2O3) = –412.8 ± 0.5 кДж/моль, энтальпия растворения оксида диспрозия (Dy2O3) в 4 M HCl взята из работы [63] и составила ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{3b}}}}^{0}$ (Dy2O3) = –385.11 ± 3.41 кДж/моль. Энтальпия растворения оксида эрбия в 4 М HCl равна ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{3b}}}}^{0}$(Er2O3) = –377.81 ± 3.28 кДж/моль [39–42], энтальпия растворения соединения Bi3Nb0.2Sm0.8O6.2 – ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{4b}}}}^{0}$(Bi3Nb0.2Sm0.8O6.2) = = −474.4 ± 4.6 кДж/моль [39–42]. Энтальпия растворения ниобата висмута, замещенного диспрозием (Bi3Nb0.2Dy0.8O6.2), в 4 M HCl составила: ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{4b}}}}^{0}$ (Bi3Nb0.2Dy0.8O6.2) = –469.75 ± 5.27 кДж/моль [39–42], энтальпия растворения соединения Bi3Nb0.2Er0.8O6.2 – ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{4b}}}}^{0}$(Bi3Nb0.2Er0.8O6.2) = = −452.57 ± 5.59 кДж/моль [39–42].

При рассмотрении энтальпий растворения оксидов РЗЭ и ниобатов висмута, замещенных редкоземельными элементами, можно выявить следующие закономерности. Энтальпии растворения исследуемых оксидов РЗЭ уменьшаются по абсолютной величине от оксида самария до оксида эрбия. Это коррелирует с уменьшением радиуса РЗЭ.

Далее авторы [39–42] разработали термохимический цикл, который позволял на основе измеренной энтальпии реакции (5b) (${{\Delta }_{r}}H_{{{\text{5b}}}}^{0}$) рассчитать стандартные энтальпии образования (${{\Delta }_{f}}H_{{{\text{11b}}}}^{0}$) для соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er). Цикл представлен ниже.

(6b)
$\begin{gathered} {\text{1}}{\text{.5B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + 0.4{\text{R}}{{{\text{E}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + \\ {\text{ + }}\,\,{\text{0}}{\text{.5}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {\text{ж}} \right) = {\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}\left( {{\text{тв}}} \right) + \\ + \,\,{\text{HCl}}\left( {{\text{р - р}}} \right) + {{\Delta }_{r}}H_{{{\text{5b}}}}^{0}, \\ \end{gathered} $
(7b)
${\text{3Bi}}\left( {{\text{тв}}} \right) + 2.2{\text{5}}{{{\text{O}}}_{{\text{2}}}}\left( {\text{г}} \right) = 1.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 1.5{{\Delta }_{r}}H_{{{\text{6b}}}}^{0},$
(8b)
$\begin{gathered} 0.2{\text{Nb}}\left( {{\text{тв}}} \right) + 0.5{\text{C}}{{{\text{l}}}_{{\text{2}}}}\left( {\text{г}} \right) = \\ = \,\,0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + 0.2{{\Delta }_{r}}H_{{{\text{7b}}}}^{0}, \\ \end{gathered} $
(9b)
$\begin{gathered} {\text{0}}{\text{.8RE}}\left( {{\text{тв}}} \right) + 0.6{{{\text{O}}}_{2}}\left( {\text{г}} \right) = \\ = \,\,0.4{\text{R}}{{{\text{E}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 0.4{{\Delta }_{r}}H_{{{\text{8b}}}}^{0}, \\ \end{gathered} $
(10b)
$\begin{gathered} 0.5{{{\text{H}}}_{{\text{2}}}}\left( {\text{г}} \right) + 0.25{{{\text{O}}}_{2}}\left( {\text{г}} \right) = \\ = 0.5{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {\text{ж}} \right) + 0.5{{\Delta }_{r}}H_{{{\text{9b}}}}^{0}, \\ \end{gathered} $
(11b)
$\begin{gathered} 0.5{{{\text{H}}}_{{\text{2}}}}\left( {\text{г}} \right) + 0.5{\text{C}}{{{\text{l}}}_{{\text{2}}}}\left( {\text{г}} \right) = \\ = \,\,{\text{HCl(р - р, }}4\,\,{\text{M}}) + {{\Delta }_{r}}H_{{{\text{10b}}}}^{0}, \\ \end{gathered} $
(12b)
$\begin{gathered} {\text{3Bi}}\left( {{\text{тв}}} \right) + 0.2{\text{Nb}}\left( {{\text{тв}}} \right) + 0.8{\text{RE}}\left( {{\text{тв}}} \right) + \\ + \,\,3.1{{{\text{O}}}_{{\text{2}}}}\left( {\text{г}} \right) = \,{\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}\left( {{\text{тв}}} \right) + {{\Delta }_{r}}H_{{{\text{11b}}}}^{0}. \\ \end{gathered} $

Авторы [39–42] рассчитали стандартные энтальпии образования соединений Bi3Nb0.2RE0.8O6.2 по схеме:

$\begin{gathered} {{\Delta }_{r}}H_{{{\text{5b}}}}^{0} = {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) + \\ + \,\,{{\Delta }_{f}}{{H}^{0}}({\text{HCl}},{\text{ }}4\,\,{\text{M}})--\,1.5{{\Delta }_{f}}{{H}^{0}}{\text{(B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{3}})-- \\ - \,\,0.2{{\Delta }_{f}}{{H}^{0}}({\text{NbC}}{{{\text{l}}}_{{\text{5}}}})-- \\ - \,\,0.4{{\Delta }_{f}}{{H}^{0}}({\text{R}}{{{\text{E}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}{\text{)}}--0.5{{\Delta }_{f}}{{H}^{0}}({{{\text{H}}}_{{\text{2}}}}{\text{O}}). \\ \end{gathered} $

Стандартные энтальпии образования соединений, необходимые для расчета стандартных энтальпий образования ниобатов висмута (Bi3Nb0.2RE0.8O6.2), были взяты авторами [39–42] из справочника [55]: ΔfH0(Bi2O3, тв) = –577.8 ± ± 4.2 кДж/моль; ΔfH0(Dy2O3, тв) = –1863.4 ± ± 5.0 кДж/моль; ΔfH0(NbCl5, тв) = –797.47 ± ± 2.09 кДж/моль; ΔfH0(H2O, ж) = –285.83 ± ± 0.04 кДж/моль; ΔfH0(HCl, р-р) = –162.80 ± ± 0.42 кДж/моль; ΔfH0(Sm2O3, тв) = –1823.0 ± ± 4.0 кДж/моль (моноклинная модификация); ΔfH0(Er2O3, тв) = –1897.9 ± 2.1 кДж/моль.

С использованием вышеприведенных данных авторы [39–42] рассчитали стандартные энтальпии образования соединений Bi3Nb0.2Sm0.8O6.2, Bi3Nb0.2Dy0.8O6.2, Bi3Nb0.2Er0.8O6.2:

$\begin{gathered} {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{S}}{{{\text{m}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{6.2}}}) = \\ = --1749.8 \pm 8.3{\text{ кДж/моль}}; \\ {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{D}}{{{\text{y}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = \\ = --1759.5 \pm 9.2{\text{ кДж/моль;}} \\ {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{E}}{{{\text{r}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = \\ = --1787.5 \pm 8.9{\text{ кДж/моль}}{\text{.}} \\ \end{gathered} $

Второй термохимический цикл для определения стандартной энтальпии образования ниобата висмута, замещенного лютецием (Bi3Nb0.2Lu0.8O6.2), представлен авторами [39–42] в следующем виде:

(1с)
$\begin{gathered} 1.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + 9{\text{HCl}}\left( {{\text{р - р}}} \right) + {\text{раствор }}1 = \\ = \,\,3{\text{BiC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + 4.5{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}2 + 1.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{1с}}}}^{0},~~~~~~~~ \\ \end{gathered} $
(2с)
$\begin{gathered} 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + {\text{раствор }}2 = 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}3 + 0.2{{\Delta }_{{{\text{sol}}}}}H_{{{\text{2с}}}}^{0}, \\ \end{gathered} $
(3с)
$\begin{gathered} 0.8{\text{Lu}}\left( {{\text{тв}}} \right) + 2.{\text{4HCl}}\left( {{\text{р - р}}} \right) + {\text{раствор }}3 = \\ = \,\,0.{\text{8LuC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + 1.2{{{\text{H}}}_{{\text{2}}}}\left( {\text{г}} \right) + \\ + \,\,{\text{раствор }}4 + 0.4{{\Delta }_{{{\text{sol}}}}}H_{{{\text{3с}}}}^{0}, \\ \end{gathered} $
(4с)
$\begin{gathered} {\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{L}}{{{\text{u}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}\left( {{\text{тв}}} \right) + {\text{12}}{\text{.4HCl}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}1 = 3{\text{BiC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + 0.2{\text{NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{р - р}}} \right) + \\ + \,\,0.8{\text{LuC}}{{{\text{l}}}_{{\text{3}}}}\left( {{\text{р - р}}} \right) + 6.{\text{2}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {{\text{р - р}}} \right) + \\ + \,\,{\text{раствор }}4 + {{\Delta }_{{{\text{sol}}}}}H_{{{\text{4с}}}}^{0}. \\ \end{gathered} $

На основании приведенных выше реакций с использованием закона Гесса авторы [39–42] записали:

(5с)
$\begin{gathered} 1.{\text{5B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}\left( {{\text{тв}}} \right) + {\text{0}}{\text{.2NbC}}{{{\text{l}}}_{{\text{5}}}}\left( {{\text{тв}}} \right) + 0.{\text{8Lu}}\left( {{\text{тв}}} \right) + \\ + \,\,1.{\text{7}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}\left( {\text{ж}} \right) = {\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{L}}{{{\text{u}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}\left( {{\text{тв}}} \right) + \\ + \,\,{\text{HCl}}\left( {{\text{р - р}}} \right) + 1.2{{{\text{H}}}_{2}}\left( {\text{г}} \right) + {{\Delta }_{r}}H_{{{\text{5с}}}}^{0}, \\ \end{gathered} $
где ${{\Delta }_{r}}H_{{{\text{5c}}}}^{0}$ = $ - {{\Delta }_{{{\text{sol}}}}}H_{{{\text{4c}}}}^{0}$ + $1.5{{\Delta }_{{{\text{sol}}}}}H_{{{\text{1c}}}}^{0}$ + $0.2{{\Delta }_{{{\text{sol}}}}}H_{{{\text{2c}}}}^{0}$ + + $0.4{{\Delta }_{{{\text{sol}}}}}H_{{{\text{3c}}}}^{0}$.

Для расчета авторы [39–42] взяли энтальпии растворения в 4 M соляной кислоте для Bi2O3, NbCl5, представленные выше; энтальпия растворения Lu в 4 M HCl заимствована из работы [64] и составила ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{3c}}}}^{0}$ = –703.30 ± 2.50 кДж/моль. Энтальпия растворения Bi3Nb0.2Lu0.8O6.2 в 4 M HCl определена авторами [39–42] как ${{\Delta }_{{{\text{sol}}}}}H_{{{\text{4c}}}}^{0}$ = –432.72 ± ± 5.43 кДж/моль. Полученная в результате расчета стандартная энтальпия образования Bi3Nb0.2Lu0.8O6.2 составила ΔfH0(Bi3Nb0.2Lu0.8O6.2) = –1802.76 ± ± 8.74 кДж/моль.

При рассмотрении энтальпий растворения ниобатов висмута, замещенных редкоземельными элементами, наблюдается следующая закономерность. Энтальпии растворения ниобатов висмута, замещенных редкоземельными элементами, уменьшаются по абсолютной величине от ниобата висмута, замещенного самарием, до ниобата висмута, замещенного лютецием. Это коррелирует с уменьшением радиуса РЗЭ.

Энтальпия решетки

Одной из важных энергетических характеристик соединений является энтальпия решетки. Энтальпия решетки – это энтальпия процесса образования кристаллической решетки из ионов. Эта характеристика связана со структурой, поскольку расчет включает энтальпии образования ионов, образующих кристаллическую решетку. Авторы работ [39–42] рассчитали энтальпии решеток для соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu) на основе измеренных стандартных энтальпий образования этих соединений с использованием цикла Борна–Габера.

$\begin{gathered} 3{\text{Bi}}\left( {{\text{тв}}} \right) + 0.2{\text{Nb}}\left( {{\text{тв}}} \right) + 0.8{\text{RE}}\left( {{\text{тв}}} \right) + 3.1{{{\text{O}}}_{2}}\left( {\text{г}} \right) = \\ = \,\,{\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{D}}{{{\text{y}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{6.2}}}\left( {{\text{тв}}} \right) + {{\Delta }_{f}}{{H}^{0}}, \\ 3{\text{Bi}}\left( {{\text{тв}}} \right) = 3{\text{B}}{{{\text{i}}}^{{3 + }}}\left( {\text{г}} \right) + 3{{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}^{{3 + }}}), \\ 0.2{\text{Nb}}\left( {{\text{тв}}} \right) = 0.2{\text{N}}{{{\text{b}}}^{{5 + }}}\left( {\text{г}} \right) + 0.2{{\Delta }_{f}}{{H}^{0}}({\text{N}}{{{\text{b}}}^{{5 + }}}), \\ 0.8{\text{RE}}\left( {{\text{тв}}} \right) = 0.8{\text{R}}{{{\text{E}}}^{{3 + }}}\left( {\text{г}} \right) + 0.8{{\Delta }_{f}}{{H}^{0}}({\text{R}}{{{\text{E}}}^{{3 + }}}), \\ 3.1{{{\text{O}}}_{2}}\left( {\text{г}} \right) = 6.2{{{\text{O}}}^{{2--}}}\left( {\text{г}} \right) + 6.2{{\Delta }_{f}}{{H}^{0}}({{{\text{O}}}^{{2--}}}), \\ 3{\text{B}}{{{\text{i}}}^{{{\text{3 + }}}}}\left( {\text{г}} \right) + 0.2{\text{N}}{{{\text{b}}}^{{5 + }}}\left( {\text{г}} \right) + 0.8{\text{R}}{{{\text{E}}}^{{{\text{3 + }}}}}\left( {\text{г}} \right) + 6.2{{{\text{O}}}^{{2--}}}\left( {\text{г}} \right) = \\ = \,\,{\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{6.2}}}\left( {{\text{тв}}} \right) + {{\Delta }_{{{\text{lat}}}}}{{H}^{0}}, \\ {{\Delta }_{{{\text{lat}}}}}{{H}^{0}} = {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{6.2}}})--3{{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}^{{3 + }}})-- \\ - \,\,0.2{{\Delta }_{f}}{{H}^{0}}({\text{N}}{{{\text{b}}}^{{5 + }}})--0.8{{\Delta }_{f}}{{H}^{0}}({\text{R}}{{{\text{E}}}^{{3 + }}})-- \\ - \,\,6.2{{\Delta }_{f}}{{H}^{0}}({{{\text{O}}}^{{2--}}}). \\ \end{gathered} $

Данные для энтальпий образования ионов были взяты из справочника [55] и составили: ΔfH0(Bi3+) = = 4994 кДж/моль; ΔfH0(Nb5+) = 13753 кДж/моль; ΔfH0(Sm3+) = 4075 кДж/моль; ΔfH0(Dy3+) = = 4189 кДж/моль; ΔfH0(Er3+) = 4251 кДж/моль; ΔfH0(Lu3+) = 4334 кДж/моль; ΔfH0(O2–) = = 906 кДж/моль.

Видно, что энтальпии образования ионов РЗЭ увеличиваются по абсолютной величине от самария до лютеция, что коррелирует с уменьшением радиуса редкоземельного элемента.

Энтальпии решеток, рассчитанные с использованием этих данных, приведены в разделе “Закономерности изменения стандартных энтальпий образования и энтальпий решетки”.

Теплоемкость

В работах [40, 41, 43, 65] была измерена теплоемкость соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu) методом дифференциальной сканирующей калориметрии. Теплоемкость определяли сравнительным методом, когда измеряли разницу между сигналами тигля с веществом и пустым тиглем. Далее определяли теплоемкость вещества на основе теплоемкости стандартного соединения, в качестве которого был выбран корунд (Al2O3). Измерения для образцов Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu) осуществляли на установке DSC 404 F1 с использованием платиновых тиглей с корундовыми вкладышами и платиновых крышек со скоростью нагрева 6 град/мин в проточной атмосфере аргона (20 мл/мин). Образцы взвешивали на электронных весах AND GH-252 с погрешностью не более 0.03 мг. Перед проведением каждого термического цикла рабочий объем установки откачивали до вакуума 1 Па и несколько раз промывали аргоном, чистота которого составляла 99.992 об. %, а основными примесями являлись: O2 – 0.0001%; N2 – 0.0005%; H2O – 0.0004%; CO2 – 0.00002%; CH4 – 0.0001%; H2 – 0.0001%. Погрешность измерения для данной установки оценивается в 2–3%, что было подтверждено экспериментами с образцами высокочистой платины и сапфира.

Проводилось три термических цикла нагрева–охлаждения. При этом данные, полученные в последовательных термических циклах (без учета первого нагрева), очень хорошо согласуются между собой.

Калибровки по тепловому потоку и температуре были выполнены согласно инструкции по использованию калориметра DSC 404 F1. Калибровки проводили при той же скорости и том же составе газа, что и эксперименты. Для выполнения калибровок определяли температуры и энтальпии плавления рекомендованных веществ. Для калибровок использовали следующие стандартные вещества: In, Bi, Sn, Pb, Zn, Al, Ag, Au. Образцы были подготовлены следующим образом. Из синтезированных таблеток были вырезаны цилиндры диаметром 5 мм и высотой не более 1.5 мм со шлифованным основанием, что обеспечивало хороший тепловой контакт с дном тигля.

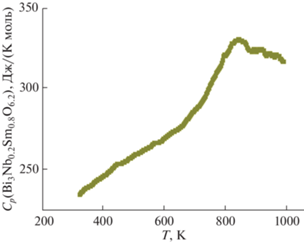
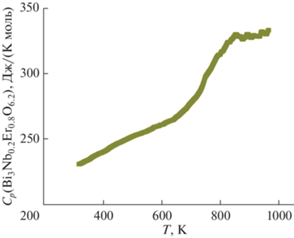
Теплоемкость ниобата висмута, замещенного самарием (Bi3Nb0.2Sm0.8O6.2), была исследована в температурном интервале 320–997 K. Теплоемкость меняется плавно до 650 K, дальше начинается фазовый переход. Температура фазового перехода оценивается в 850 K. Температурная зависимость теплоемкости соединения Bi3Nb0.2Sm0.8O6.2 представлена на рис. 3.

Рис. 3.

Температурная зависимость теплоемкости Bi3Nb0.2Sm0.8O6.2. Данные работ [39–41, 43].

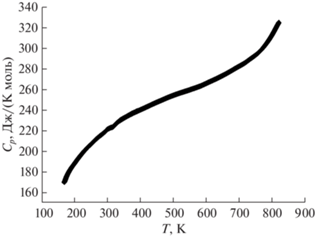
Авторами [40] впервые с использованием метода дифференциальной сканирующей калориметрии была измерена температурная зависимость теплоемкости для Bi3Nb0.2Dy0.8O6.2 в интервале температур 167–818 K. Погрешность измерений не превышала 1–2%. Авторы обнаружили, что теплоемкость соединения Bi3Nb0.2Dy0.8O6.2 содержит аномалию выше 500 K. Теплоемкость представлена на рис. 4. Ввиду наличия фазового перехода авторы [40] рекомендовали применение этого соединения в интервале температур 167–500 K. Изначально соединение Bi3Nb0.2Dy0.8O6.2 имеет кубическую структуру (δ-форма оксида висмута). Известно, что существует переход δ-формы оксида висмута в тетрагональную форму [66–68]. Поэтому авторы работы [40] допустили, что наблюдаемый в соединении Bi3Nb0.2Dy0.8O6.2 переход связан с переходом кубической структуры в тетрагональную структуру. Измеренная авторами теплоемкость при стандартных условиях составила Cp(298.15) = = 222.07 Дж/(K моль). Измеренная теплоемкость находится в хорошем согласии с теплоемкостью, оцененной из простых оксидов (Bi2O3, Nb2O5, Dy2O3): Cp(оцененная) = 230.42 Дж/(K моль). Теплоемкость оценена как сумма теплоемкостей простых оксидов по уравнению: Cp(Bi3Nb0.2Dy0.8O6.2) = = 1.5Cp(Bi2O3) + 0.1Cp(Nb2O5) + 0.4Cp(Dy2O3).

Рис. 4.

Температурная зависимость теплоемкости Bi3Nb0.2Dy0.8O6.2. Данные работ [39–41, 43].

Теплоемкость Bi3Nb0.2Er0.8O6.2 была измерена [43] в интервале температур 318–965 K и менялась монотонно от 230.9 до 264.8 Дж/(K моль) (T = 318–640 K), далее начинался фазовый переход. Температура фазового перехода для ниобата висмута, замещенного эрбием, составляла 850 K. Температурная зависимость представлена на рис. 5.

Рис. 5.

Температурная зависимость теплоемкости Bi3Nb0.2Er0.8O6.2. Данные работ [39–41, 43].

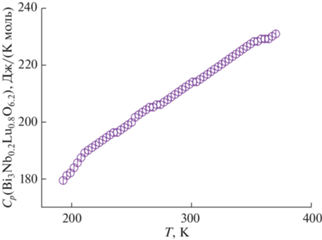
В работах [43, 65] ниобат висмута, замещенный лютецием (Bi3Nb0.2Lu0.8O6.2), был измерен в двух температурных интервалах: 190–370 и 320–970 K. Согласно полученным данным, в интервале температур 190–370 K теплоемкость плавно меняется от 173.3 до 230.6 Дж/(K моль) и отсутствуют какие-либо аномалии, связанные с фазовыми переходами. Температурная зависимость теплоемкости ниобата висмута, замещенного лютецием, представлена на рис. 6. Теплоемкость ниобата висмута, замещенного лютецием, при стандартных условиях равна Сp(Bi3Nb0.2Lu0.8O6.2, 298.15 К) = = 212.9 ± 3.2 Дж/(K моль).

Рис. 6.

Температурная зависимость теплоемкости Bi3Nb0.2Lu0.8O6.2 (низкотемпературная часть). Данные работ [39–41, 43].

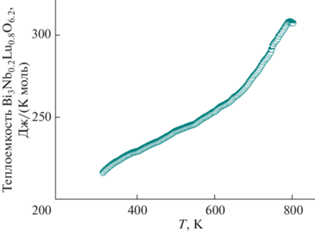
Для высокотемпературного интервала теплоемкости Bi3Nb0.2Lu0.8O6.2 наблюдалась немонотонная зависимость. Теплоемкость увеличивалась более чем на 20%. Температурная зависимость представлена на рис. 7. Температура фазового перехода составляет 791 K, что на 60 K ниже, чем для ниобатов висмута, замещенных самарием и эрбием.

Рис. 7.

Температурная зависимость теплоемкости Bi3Nb0.2Lu0.8O6.2 (высокотемпературная часть). Данные работ [39–41, 43].

Закономерности изменения стандартных энтальпий образования и энтальпий решетки

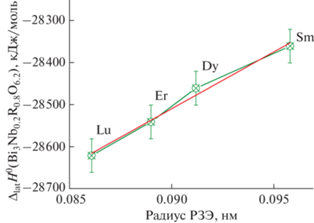
Одной из важных областей термодинамики является предсказательная термодинамика”, развитая в работах проф. Глассера [69–71] и продолженная авторами настоящего обзора [72–74]. “Предсказательная термодинамика” позволяет прогнозировать свойства неизученных соединений. Как известно, редкоземельных элементов больше 10. Измерить свойства всех соединений с редкоземельными элементами – довольно трудоемкая задача, поэтому в данном случае целесообразно использовать аппарат “предсказательной термодинамики”. Анализ термодинамических данных начнем с энтальпии решетки. Авторы работ [39–42] рассчитали энтальпии решеток для ниобатов висмута, замещенных самарием, диспрозием, эрбием, лютецием как следующие величины:

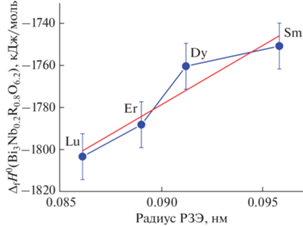
$\begin{gathered} \begin{array}{*{20}{l}} {{{\Delta }_{{lat}}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{S}}{{{\text{m}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = --28{\kern 1pt} 360{\text{ кДж/моль}},} \\ {{{\Delta }_{{lat}}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{D}}{{{\text{y}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = --28{\kern 1pt} 460{\text{ кДж/моль}},} \\ {{{\Delta }_{{lat}}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{E}}{{{\text{r}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = --28{\kern 1pt} 540{\text{ кДж/моль}},} \end{array} \\ {{\Delta }_{{lat}}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{L}}{{{\text{u}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = --28{\kern 1pt} 620{\text{ кДж/моль}}. \\ \end{gathered} $

Видно, что энтальпии решеток увеличиваются с уменьшением радиуса РЗЭ. Величины радиусов РЗЭ взяты из работы [75]: r(Sm3+) = 0.0958 нм; r(Dy3+) = 0.0912 нм; r(Er3+) = 0.0890 нм; r(Lu3+) = = 0.0861 нм. Величины радиусов приведены для КЧ = 6, что соответствует структуре изученных оксидов. Ниже на рис. 8 приведена зависимость энтальпий решеток от радиуса РЗЭ для соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu).

Рис. 8.

Зависимость энтальпии решетки Bi3Nb0.2RE0.8O6.2 от радиуса редкоземельного элемента. Данные работ [39–41].

Следует отметить, что зависимость энтальпий решеток от радиусов РЗЭ является практически линейной. Чтобы объяснить линейный характер этой зависимости, обратимся к формуле Капустинского для энергии решетки. Энергия решетки – это величина, обратная по знаку энтальпии решетки.

$U = 1070.9\frac{{m{{Z}_{{\text{a}}}}{{Z}_{{\text{k}}}}}}{{{{r}_{{\text{a}}}} + {{r}_{{\text{k}}}}}},$
где m – количество ионов; Za – заряд аниона; Zk – заряд катиона; ra – радиус аниона; rk – радиус катиона.

Соединения Bi3Nb0.2RE0.8O6.2 имеют одинаковый состав, за исключением редкоземельных элементов. Для малых замещений можно разложить формулу Капустинского в ряд по радиусам РЗЭ. В таком случае можно получить: U = A + B*r, где r – радиус РЗЭ. Таким образом, для малых замещений энергия решетки (энтальпия решетки) является линейной функцией радиуса редкоземельного элемента. Это подтверждено построенной линейной зависимостью, представленной на рис. 8.

Далее обратимся к анализу стандартных энтальпий образования. В работе [56] была определена стандартная энтальпия образования для соединения BiNbO4: ΔfH0(BiNbO4) = –1279.7 ± 11.5 кДж/моль. В работах [39–42] были измерены стандартные энтальпии образования соединений Bi3Nb0.2RE0.8O6.2. Получены следующие данные для стандартных энтальпий образования [39–42]:

$\begin{array}{*{20}{l}} \begin{gathered} {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{S}}{{{\text{m}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = \\ = --1749.8 \pm 8.3{\text{ кДж/моль,}} \\ \end{gathered} \\ \begin{gathered} {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{D}}{{{\text{y}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = \\ = --1759.5 \pm 9.2{\text{ кДж/моль}}, \\ \end{gathered} \\ \begin{gathered} {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{E}}{{{\text{r}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{6.2}}}) = \\ = --1787.5 \pm 8.9{\text{ кДж/моль}}, \\ \end{gathered} \\ \begin{gathered} {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{L}}{{{\text{u}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{{\text{6}}{\text{.2}}}}}) = \\ = --1802.8 \pm 8.7{\text{ кДж/моль}}{\text{.}} \\ \end{gathered} \end{array}$

Видно, что стандартная энтальпия образования незамещенного ниобата висмута состава BiNbO4 по абсолютной величине меньше, чем стандартные энтальпии образования ниобатов висмута, замещенных редкоземельными элементами, состава Bi3Nb0.2RE0.8O6.2. Объяснить этот факт на данном этапе не представляется возможным, поскольку соединения имеют разный состав.

Рассмотрение стандартных энтальпий образования соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu) показало, что эта величина увеличивается с уменьшением радиуса РЗЭ. Величины радиусов РЗЭ были взяты из работы [75] и составили: r(Sm3+) = 0.0958 нм; r(Dy3+) = 0.0912 нм; r(Er3+) = 0.0890 нм; r(Lu3+) = = 0.0861 нм. На рис. 9 представлен график зависимости стандартных энтальпий образования соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu) от радиуса РЗЭ. Видно, что зависимости близки к линейным.

Рис. 9.

Зависимость стандартной энтальпии образования Bi3Nb0.2RE0.8O6.2 от радиуса редкоземельного элемента. Данные работ [39–41].

Для объяснения линейной зависимости стандартных энтальпий образования от радиуса РЗЭ обратимся к ранее приведенной формуле для энтальпии решетки от радиуса РЗЭ. Энтальпия решетки является линейной функцией от радиуса РЗЭ при малых замещениях и, как показано в работе [76], может быть выражена формулой: ΔlatH0 = A + B*r, где r – радиус РЗЭ. Стандартная энтальпия образования ниобатов висмута, замещенных редкоземельными элементами, может быть записана в виде:

$\begin{gathered} {{\Delta }_{{{\text{lat}}}}}{{H}^{0}} = {{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}_{{\text{3}}}}{\text{N}}{{{\text{b}}}_{{{\text{0}}{\text{.2}}}}}{\text{R}}{{{\text{E}}}_{{{\text{0}}{\text{.8}}}}}{{{\text{O}}}_{{6.2}}})-- \\ - \,\,3{{\Delta }_{f}}{{H}^{0}}({\text{B}}{{{\text{i}}}^{{{\text{3 + }}}}})--0.2{{\Delta }_{f}}{{H}^{0}}({\text{N}}{{{\text{b}}}^{{5 + }}})-- \\ - \,\,0.8{{\Delta }_{f}}{{H}^{0}}({\text{R}}{{{\text{E}}}^{{3 + }}})--6.2{{\Delta }_{f}}{{H}^{0}}({{{\text{O}}}^{{2--}}}). \\ \end{gathered} $

Из вышеприведенной формулы можно выразить стандартную энтальпию образования через энтальпию решетки и энтальпии образования ионов РЗЭ: ΔfH0(Bi3Nb0.2RE0.8O6.2) = ΔlatH0 + С + +  0.8 ΔfH0(RE3+), где С – постоянная величина для данных соединений. Как было показано в работе [76], зависимость энтальпий образования ионов редкоземельных элементов от их радиусов является линейной, т.е. может быть выражена следующим образом: ΔfH0(RE3+) = D + E*r. Тогда, подставляя в вышеприведенную формулу выражения для энтальпии решетки и энтальпии образования ионов, получим ΔfH0(Bi3Nb0.2RE0.8O6.2) = A + B*r + + С + 0.8* (D + E*r) или ΔfH0(Bi3Nb0.2RE0.8O6.2) = F + + J*r. Это подтверждает рис. 9.

Ионная проводимость и корреляция со структурой

В настоящем разделе будут приведены некоторые работы, посвященные ионной проводимости и корреляциям со структурой для ниобатов висмута, замещенных редкоземельными элементами.

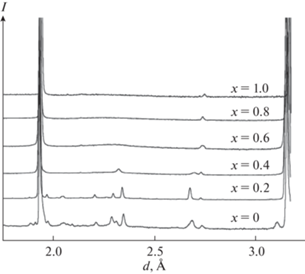
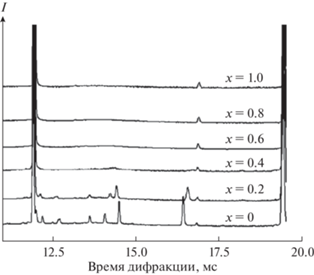
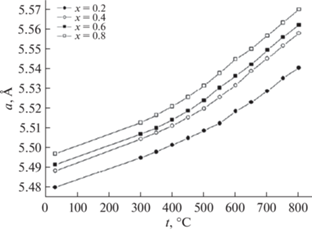
Авторы [27–30] исследовали ниобаты висмута, замещенные иттрием, состава Bi3Nb1 –xYxO7– x (0 < x < 1). Исследования проводили методами импедансной спектроскопии, рентгенофазового анализа и нейтронной дифракциией. Авторами были синтезированы керамические соединения состава Bi3Nb1 –xYxO7 –x, которые имели кубическую структуру δ-формы оксида висмута. На рис. 10 представлена нейтронография полученных образцов при комнатной температуре, а на рис. 11 – зависимость параметров кубической структуры соединений Bi3Nb1 –xYxO7 –x (0 < x < 1) от состава. Как видно из рис. 11, параметр структуры увеличивается с увеличением х от 5.465 до 5.490 Å. Это связано с тем, что радиус иттрия (r(Y3+) = 0.9 Å) больше, чем ниобия (r(Nb5+) = 0.64 Å).

Рис. 10.

Нейтронограммы соединений Bi3Nb1 ‒ xYxO7 –x. Данные работ [27–30].

Рис. 11.

Зависимость параметров структуры Bi3Nb1 ‒ xYxO7 –x от состава. Данные работ [27–30].

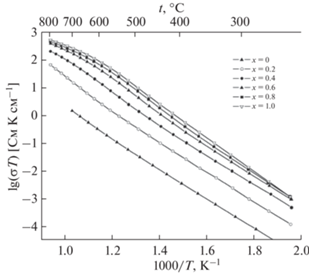
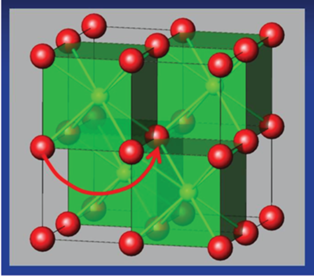
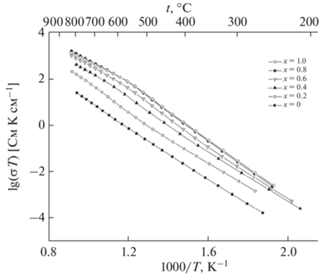
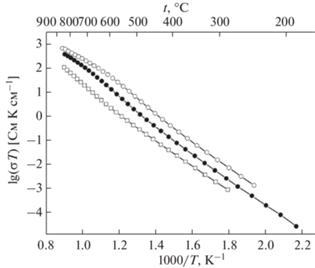
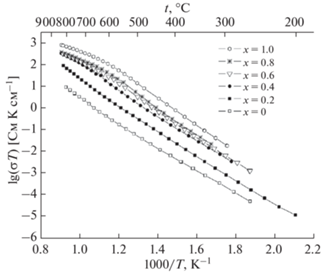
Далее авторы [27–30] с использованием импедансной спектроскопии измерили проводимость соединений Bi3Nb1 –xYxO7 –x (0 < x < 1) в интервале температур 523–1073 K. Температурная зависимость проводимости представлена на рис. 12, из которого видно, что проводимость увеличивается с ростом содержания иттрия. Предложим этому явлению следующее объяснение. Поскольку иттрий имеет больший ионный радиус, чем ниобий, с увеличением содержания иттрия, следуя формуле Капустинского для энергии решетки, энергия решетки уменьшается, т.е. соединение становится менее стабильным. В менее стабильном соединении миграция атомов, которая обусловливает ионную проводимость, является более свободной, с чем и связано увеличение проводимости. В работе [77] представлен механизм ионной проводимости δ-формы оксида висмута. Одним из ионов (рис. 13), который обусловливает проводимость, является ион кислорода. Если решетка соединения менее устойчива, то ионам легче перемещаться, этим можно объяснить увеличение проводимости с ростом содержания иттрия в соединениях Bi3Nb1 –xYxO7 –x (0 < x < 1).

Рис. 12.

Температурные зависимости проводимости Bi3Nb1 –xYxO7 –x. Данные работ [27–30].

Рис. 13.

Механизм ионной проводимости. Данные работы [77].

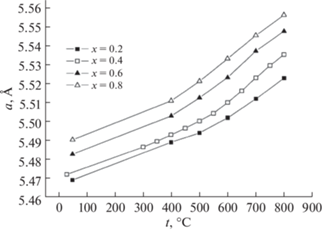
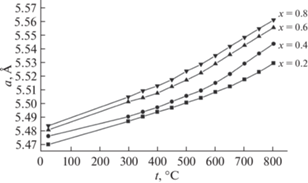
В работах [27–30] также показано, что энергия активации увеличивается с ростом содержания иттрия. График зависимости представлен на рис. 14. Кроме того, авторы [27–30] изучили температурную зависимость параметров решетки соединения Bi3Nb1 –xYxO7 –x от содержания иттрия. Они показали, что с повышением температуры параметр решетки увеличивается (рис. 15).

Рис. 14.

Зависимость энергии активации Bi3Nb1 –xYxO7 –x от содержания Y. Данные работ [27–30].

Рис. 15.

Зависимость параметров решетки Bi3Nb1 ‒ xYxO7 –x от температуры. Данные работ [27–30].

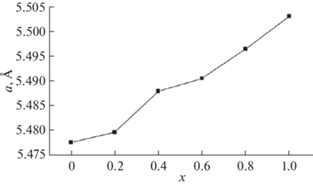
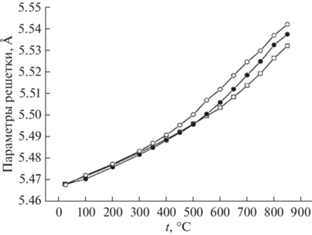
Авторы [31] синтезировали новые соединения состава Bi7Nb2 – 2xY2xO15.5 – 2x (0< x < 1), изучили их структуру, а также ионную проводимость. Исследование выполнено с помощью рентгенофазового анализа, нейтронной дифракции и импедансной спектроскопии. Детали метода нейтронной дифракции представлены на рис. 16. Как оказалось, соединения всех составов (пр. гр. Fm$\bar {3}$m) имеют кубическую структуру, это структура δ-формы оксида висмута. Исследование параметров решетки (рис. 17) показало, что параметр решетки увеличивается от 5.475 до 5.505 Å при изменении состава Bi7Nb2 – 2xY2xO15.5 – 2x от x = 0 до 1. Далее были изучены температурные зависимости параметров решетки. Установлено (рис. 18), что с повышением температуры параметры решетки увеличиваются.

Рис. 16.

Нейтронограммы Bi7Nb2 – 2xY2xO15.5 – 2x. Данные работы [31].

Рис. 17.

Параметры решетки Bi7Nb2 – 2xY2xO15.5 – 2x. Данные работы [31].

Рис. 18.

Температурные зависимости параметров решетки Bi7Nb2 – 2xY2xO15.5 – 2x. Данные работы [31].

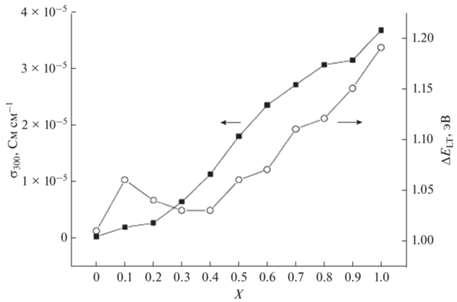
Далее авторы [31] изучили ионную проводимость соединений Bi7Nb2 – 2xY2xO15.5 – 2x (0 < x < 1) в интервале температур 200–900°С. Графики зависимостей проводимости представлены на рис. 19, 20. Показано, что проводимость увеличивается с температурой и с ростом содержания иттрия. Увеличение проводимости для соединений Bi7Nb2 – 2xY2xO15.5 – 2x с ростом содержания иттрия можно объяснить так же, как это было сделано ранее для соединений Bi3Nb1 –xYxO7 –x.

Рис. 19.

Температурные зависимости проводимости Bi7Nb2 – 2xY2xO15.5 – 2x. Данные работы [31].

Рис. 20.

Зависимости проводимости Bi7Nb2 – 2xY2xO15.5 – 2x от содержания иттрия. Данные работы [31].

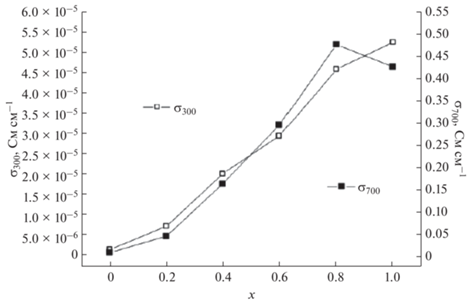
В работе [32] были синтезированы соединения в системе Bi3NbO7–Bi3YbO6 и выполнены исследования их структуры, а также ионной проводимости. Авторы методом твердофазных реакций из оксида висмута, оксида ниобия, оксида иттербия синтезировали соединения состава Bi3Nb1 –xYbxO7 –x (x = 0.2–0.8). Структурные исследования проводили методами рентгенофазового анализа и нейтронографии. С помощью импедансной спектроскопии исследованы температурные зависимости ионной проводимости. Как показал структурный анализ, соединения Bi3Nb1 –xYbxO7 –x имеют кубическую структуру (пр. гр. Fm3m (рис. 21)). Параметры кубической ячейки увеличиваются с температурой и ростом содержания иттербия (рис. 22). Температурная зависимость ионной проводимости была измерена в интервале температур 200–900°С. Как показано на рис. 23, величина ионной проводимости увеличивается с повышением температуры. Величина ионной проводимости при одной и той же температуре для соединений Bi3Nb1 –xYbxO7 –x увеличивается с ростом х в пределе от 0.2 до 0.6 (рис. 23). Как показано в работе [75], радиус иттербия (r(Yb3+) = 0.868 Å) больше, чем радиус ниобия (r(Nb5+) = 0.64 Å), поэтому с увеличением содержания иттербия энтальпия решетки уменьшается. Это делает соединения менее стабильными и улучшает возможность миграции ионов. Последнее повышает ионную проводимость.

Рис. 21.

Дифрактограмма Bi3Nb1 –xYbxO7 –x. Данные работы [32].

Рис. 22.

Температурные зависимости структурных параметров Bi3Nb1 –xYbxO7 –x. Данные работы [32].

Рис. 23.

Температурные зависимости ионной проводимости Bi3Nb1 –xYbxO7 –x. Данные работы [32].

В работах [33, 36, 37] методом твердофазного синтеза были получены ниобаты висмута, замещенные эрбием, состава Bi3Nb1 –xErxO7 –x (x = 0.2–0.8). Исследование структуры показало, что образцы имеют кубическую структуру флюорита. На рис. 24 показана дифрактограмма полученных образцов. Изучение зависимости параметров решетки от температуры (рис. 25) показало, что параметры решетки увеличиваются с повышением температуры и ростом содержания эрбия. Методом импедансной спектроскопии была изучена ионная проводимость (рис. 26) в интервале температур 473–1173 K. Проводимость демонстрирует такое же поведение, как в случае с ниобатами висмута, замещенными иттербием. Следовательно, с повышением температуры проводимость увеличивается, так же как с ростом содержания эрбия.

Рис. 24.

Дифрактограмма Bi3Nb1 –xErxO7 –x. Данные работ [33, 36, 37].

Рис. 25.

Температурные зависимости параметров решетки Bi3Nb1 –xErxO7 –x. Данные работ [33, 36, 37].

Рис. 26.

Ионная проводимость Bi3Nb1 –xErxO7– x. Данные работ [33, 36, 37].

Рассмотрение структуры и ионной проводимости ниобатов висмута, замещенных редкоземельными элементами, позволило установить следующие закономерности. Полученные соединения имеют кубическую структуру (структура δ-формы оксида висмута, пр. гр. Fm$\bar {3}$m). Параметр решетки и ионная проводимость соединений Bi3Nb1 – xRExO7 – x (RE = Y, Er, Yb) увеличиваются с ростом содержания РЗЭ (x). Это можно объяснить тем, что радиус редкоземельного элемента больше, чем радиус ниобия. В связи с этим при замещении ниобия на редкоземельные элементы решетка становится менее стабильной и ионы, обусловливающие проводимость, могут более свободно перемещаться по решетке. В связи с этим увеличивается ионная проводимость.

ЗАКЛЮЧЕНИЕ

В обзоре рассмотрен синтез ниобатов висмута и ниобатов висмута, замещенных редкоземельными элементами. Как показало изучение литературы, основным методом синтеза является метод твердофазных реакций. В редких случаях используется золь-гель метод. Для синтеза применяются различные прекурсоры: оксиды, нитраты, цитраты. Методом твердофазного синтеза получен широкий набор соединений на основе висмута, ниобия и редкоземельных элементов следующих составов: Bi3NbO7, BiNbO4, Bi5NbO10, Bi4NbO8.5, Bi3Nb1 –xRExO7–x (RE = Y, Er, Yb), Bi7Nb2 – 2xY2xO15.5 – 2x, Bi3 –xYxNb1 –yWyO7 ± δ, Bi6.95Y0.05Nb5O15.5, Bi2.95Y0.05Nb1 –yZryO7 ± δ, Bi6.95Y0.05Nb2 –yZryO15.5, Bi3Nb0.2RE0.8O6.2 (RE = Lu, Dy, Er, Sm). Исследование соединений выполняли методами рентгенофазового и химического анализа. Показано, что соединения Bi3Nb0.2RE0.8O6.2 (RE = Lu, Dy, Er, Sm), Bi3Nb1 –xRExO7 –x (RE = Y, Er, Yb) имеют кубическую структуру, пр. гр. Fm3m.

Термодинамические данные для висмутатов ниобия практически отсутствуют. Измерена энтальпия образования только для BiNbO4. Методом реакционной калориметрии измерены стандартные энтальпии образования соединений Bi3Nb0.2RE0.8O6.2 (RE = Lu, Dy, Er, Sm). С использованием цикла Борна–Габера рассчитаны энтальпии решеток для этих соединений. Показано, что стандартные энтальпии образования и энтальпии решеток увеличиваются по абсолютной величине с уменьшением радиуса редкоземельного элемента. Теплоемкость соединений Bi3Nb0.2RE0.8O6.2 (RE = Sm, Dy, Er, Lu) измерена методом дифференциальной сканирующей калориметрии. Для всех соединений обнаружены фазовые переходы.

Для соединений Bi3Nb1 –xRExO7 –x (RE = Y, Er, Yb) изучена структура и ионная проводимость. Показано, что ионная проводимость увеличивается с ростом содержания редкоземельного элемента. Установлено, что параметр решетки увеличивается с ростом содержания редкоземельного элемента (x) в соединениях состава Bi3Nb1 –xRExO7 –x (RE = Y, Er, Yb).

Список литературы

  1. Punn R., Feteira A.M., Sinclair D.C. et al. // J. Am. Chem. Soc. 2006. V. 128. P. 15386. https://doi.org/10.1021/ja065961d

  2. Ivanov S.A., Stash A.I., Bush A.A. et al. // Russ. J. Inorg. Chem. 2022. V. 67. P. 588. https://doi.org/10.1134/S0036023622050096

  3. Matskevich N.I., Wolf T., Greaves C. et al. // J. Alloys Compd. 2014. V. 582. P. 253. https://doi.org/10.1016/j.jallcom.2013.07.135

  4. Emhjellen L.K., Xing W., Li Z. et al. // J. Membr. Sci. 2022. V. 660. P. 120875. https://doi.org/10.1016/j.memsci.2022.120875

  5. Ershov D.S., Besprozvannykh N.V., Sinel’shchikova O.Y. // Russ. J. Inorg. Chem. 2022. V. 67. P. 105. https://doi.org/10.1134/S003602362201003X

  6. Drache M., Roussel P., Wignacourt J.P. // Chem. Rev. 2007. V. 107. P. 80. https://doi.org/10.1021/cr050977s

  7. Balci M., Saatci B., Cerit S. et al. // Solid State Ionics. 2022. V. 387. P. 116060. https://doi.org/10.1016/j.ssi.2022.116060

  8. Proskurina O.V., Sokolova A.N., Sirotkin A.A. et al. // Russ. J. Inorg. Chem. 2021. V. 66. P. 163. https://doi.org/10.1134/S0036023621020157

  9. Bandyopadhyay S., Dutta A. // J. Phys. Chem. Solids. 2017. V. 102. P. 12. https://doi.org/10.1016/j.jpcs.2016.11.001

  10. Lomakin M.S., Proskurina O.V., Levin A.A. et al. // Russ. J. Inorg. Chem. 2022. V. 67. P. 820. https://doi.org/10.1134/S0036023622060134

  11. Weber M., Rodriguez R.D., Zahn D.R. et al. // Inorg. Chem. 2022. V. 61. P. 1571. https://doi.org/10.1021/acs.inorgchem.1c03330

  12. Akazawa H. // Ceram. Int. 2023. V. 49. P. 9069. https://doi.org/10.1016/j.ceramint.2022.11.064

  13. Matskevich N.I., Wolf Th., Greaves C. et al. // J. Chem. Thermodyn. 2015. V. 91. P. 234. https://doi.org/10.1016/j.jct.2015.07.036

  14. Weber M., Schlesinger M., Mehring M. // Cryst. Growth Des. 2016. V. 16. P. 5678. https://doi.org/10.1021/acs.cgd.6b00628

  15. Crumpton T.E., Mosselmans J.F.W., Greaves C. // J. Mater. Chem. 2005. V. 15. P. 164. https://doi.org/10.1039/b412108m

  16. Kekade S.S., Gaikwad P.V., Raut S.A. et al. // ACS Omega. 2018. V. 3. P. 5853. https://doi.org/10.1021/acsomega.8b00564

  17. Kaimieva O.S., Sabirova I.E., Buyanova E.S. et al. // Russ. J. Inorg. Chem. 2022. V. 67. P. 1348. https://doi.org/10.1134/S0036023622090054

  18. Wang X.P., Corbel G., Kodjikian S. et al. // J. Solid State Chem. 2006. V. 179. P. 3338. https://doi.org/10.1016/j.jssc.2006.06.031

  19. Ai Zh., Ho W., Lee Sh. // Appl. Surf. Sci. 2012. V. 263. P. 266. https://doi.org/10.1016/j.apsusc.2012.09.041

  20. Keve E.T., Skapski A.C. // J. Solid State Chem. 1973. V. 8. P. 139. https://doi.org/10.1016/0022-4596(73)90009-1

  21. Lisinska-Czekaj A., Czekaj D. // Key Eng. Mater. 2012 V. 512–515. P. 1212. https://doi.org/10.4028/www.scientific.net/KEM.512-515.1212

  22. Lisinska-Czekaj A., Czekaj D., Plewa J. // Ciencia&Tecnol. Mater. 2017. V. 29. P. e215. https://doi.org/10.1016/j.ctmat.2016.03.003

  23. Wang N., Li W., Zhao M. et al. // J. Chin. Ceram. Soc. 2003. V. 31. P. 625.

  24. Hampl M., Leither J., Ruzicka K. et al. // J. Therm. Anal. Calorim. 2007. V. 87. P. 553. https://doi.org/10.1007/s10973-006-7732-x

  25. Hou J., Vaish R., Qu Y. et al. // J. Power Sources. 2010. V. 195. P. 2613. https://doi.org/10.1016/j.jpowsour.2009.11.081

  26. Holdynski M., Sintyureva M., Liu X. et al. // J. Phys.: Condens. Matter. 2012. V. 24. P. 045904. http://dx.doi.org/0953-8984/12/045904C07

  27. Abrahams I., Kozanecka-Szmigiel A., Krok F. et al. // Solid State Ionics. 2006. V. 177. P. 1761. https://doi.org/10.1016/j.ssi.2006.01.036

  28. Abrahams I., Krok F., Kozanecka-Szmigiel A. et al. // J. Power Sources. 2007. V. 173. P. 788. https://doi.org/10.1016/j.jpowsour.2007.05.045

  29. Liu X., Abrahams I., Hull S. et al. // Solid State Ionics. 2011. V. 192. P. 176. https://doi.org/10.1016/j.ssi.2010.07.018

  30. Malys M., Holdynski M., Krok F. et al. // J. Power Sources. 2009. V. 194. P. 16. https://doi.org/10.1016/j.jpowsour.2009.01.001

  31. Krok F., Abrahams I., Holdynski M. et al. // Solid State Ionics. 2008. V. 179. P. 975. https://doi.org/10.1016/j.ssi.2008.02.015

  32. Leszczynska M., Liu X., Wrobel W. et al. // J. Mater. Chem. A. 2014. V. 2. P. 18624. https://doi.org/10.1039/c4ta03225j

  33. Leszczynska M., Holdynski M., Krok F. et al. // Solid State Ionics. 2010. V. 181. P. 796. https://doi.org/10.1016/j.ssi.2010.04.012

  34. Buyanova E.S., Kaimieva O.S., Shatokhina A.N. et al. // Russ. J. Inorg. Chem. 2016. V. 61. P. 470. https://doi.org/10.1134/S0036023616040069

  35. Buyanova E.S., Petrova S.A., Mikhailovskaya Z.A. et al. // Russ. J. Inorg. Chem. 2015. V. 60. P. 913. https://doi.org/10.1134/S0036023615080045

  36. Emel’yanova Yu.V., Mikhailovskaya Z.A., Buyanova E.S. et al. // Russ. J. Appl. Chem. 2017. V. 90. P. 354. https://doi.org/10.1134/S1070427217030053

  37. Emel’yanova Yu.V., Krylov A.A., Kazantseva A.D. et al. // Russ. J. Inorg. Chem. 2019. V. 64. P. 151. https://doi.org/10.1134/S0036023619020050

  38. Kaymieva O.S., Tarasova O.A., Shatokhina A.N. et al. // Russ. J. Electrochem. 2013. V. 49. P. 652. https://doi.org/10.1134/S1023193513070057

  39. Matskevich N.I., Semerikova A.N., Gelfond N.V. et al. // Russ. J. Inorg. Chem. 2020. V. 65. P. 743. https://doi.org/10.1134/S0036023620050162

  40. Matskevich N.I., Shlegel V.N., Stankus S.V. et al. // Mater. Today: Proceed. 2020. V. 25. P. 367. https://doi.org/10.1016/j.matpr.2019.12.092

  41. Matskevich N.I., Semerikova A.N., Zaitsev V.P. et al. // J. Solid State Chem. 2022. V. 316. P. 123584. https://doi.org/10.1016/j.jssc.2022.123584

  42. Matskevich N.I., Semerikova A.N., Gelfond N.V. et al. // Russ. J. Inorg. Chem. 2023. V. 68. P. 229. https://doi.org/10.31857/S0044457X2260150X

  43. Matskevich N.I., Stankus S.V., Samoshkin D.A. et al. // J. Phys.: Conf. Ser. 2020. V. 1677. P. 012169. https://doi.org/10.1088/1742-6596/1677/1/012169

  44. Hughes J.T., Navrotsky A. // J. Am. Chem. Soc. 2011. V. 133. P. 9184. https://doi.org/dx.doi.org/10.1021/ja202132h

  45. Novikov A.A., Belova E.V., Uspenskaya I.A. // J. Chem. Eng. Data. 2019. V. 64. P. 4230. https://doi.org/10.1021/acs.jced.9b00292

  46. Tsvetkov D.S., Mazurin M.O., Malyshkin D.A. et al. // J. Chem. Thermodyn. 2022. V. 174. P. 106857. https://doi.org/10.1016/j.jct.2022.106857

  47. Bannikov D.O., Safronov A.P., Cherepanov V.A. // Thermochim. Acta. 2006. V. 451. P. 22. https://doi.org/10.1016/j.tca.2006.08.004

  48. Matskevich N.I., Wolf Th., Pochivalov Yu.I. // Inorg. Chem. 2008. V. 47. P. 2581. https://doi.org/10.1021/ic701875h

  49. Voskanyan A.A., Jayanthi K., Navrotsky A. // Chem. Mater. 2022. V. 34. P. 10311. https://doi.org/10.1021/acs.chemmater.2c01569

  50. Sereda V.V., Tsvetkov D.S., Sednev A.L. et al. // Phys. Chem. Chem. Phys. 2018. V. 20. P. 20108. https://doi.org/10.1039/C8CP03782E

  51. Gagarin P.G., Gus’kov A.V., Gavrichev K.S. et al. // Russ. J. Inorg. Chem. 2022. V. 67. P. 1803. https://doi.org/10.1134/S0036023622601015

  52. Gagarin P.G., Guskov A.V., Guskov V.N. et al. // Russ. J. Inorg. Chem. 2022. V. 67. P. 2181. https://doi.org/10.1134/s0036023622602070

  53. Khorishilov A.V., Guskov V.N., Guskov A.V. et al. // Russ. J. Phys. Chem. A. 2022. V. 96. P. 918. https://doi.org/10.1134/s0036024422050144

  54. Jayanthi K., Neilsen G., Navrotsky A. et al. // J. Phys. Chem. C. 2023. V. 127. P. 3760. https://doi.org/10.1021/acs.jpcc.2c08217

  55. Glushko V.P. Termicheskie Konstanty Veshchestv (Thermal Constants of Substances), VINITI, Moscow. 1965–1982. Iss. 1–10.

  56. Leitner J., Nevrina M., Sedmidubsky D. et al. // J. Alloys Compd. 2011. V. 509. P. 4940. https://doi.org/10.1016/j.jallcom.2011.02.007

  57. Matskevich N.I., Wolf Th., Vyazovkin I.V. et al. // J. Alloys Compd. 2015. V. 628. P. 126. https://doi.org/10.1016/j.jallcom.2014.11.220

  58. Matskevich N.I., Matskevich M.Yu., Wolf Th. et al. // J. Alloys Compd. 2013. V. 577. P. 148. https://doi.org/10.1016/j.jallcom.2013.04.194

  59. Matskevich N.I., Bryzgalova A.N., Wolf Th. et al. // J. Chem. Thermodyn. 2012. V. 53. P. 23. https://doi.org/10.1016/j.jct.2012.04.003

  60. Kilday M.V. // J. Res. Nat. Bur. Stand. 1980. V. 85. P. 467.

  61. Gunther C., Pfestorf R., Rother M. et al. // J. Therm. Anal. Calorim. 1988. V. 33. P. 359. https://doi.org/10.1007/BF01914624

  62. Cordfunke E.H.P., Konings R.J.M. // Thermochim. Acta. 2001. V. 375. P. 65. https://doi.org/10.1016/S0040-6031(01)00510-X

  63. Hennig C., Oppermann H. // Z. Naturforsch. B. 1997.V. 52. P. 1517. https://doi.org/10.1515/znb-1997-1213

  64. Cordfunke E.H.P., Konings R.J.M. // Thermochim. Acta. 2001. V. 375. P. 17. https://doi.org/10.1016/S0040-6031(01)00509-3

  65. Мацкевич Н.И., Станкус С.В., Самошкин Д.А. et al. // XXXVI Сиб. Теплофиз. Семинар. Новосибирск, 2020. С. 265.

  66. Hervoches C.H., Greaves C. // J. Mater. Chem. 2010. V. 20. P. 6759. https://doi.org/10.1039/c0jm01385d

  67. Hervoches C.H., Greaves C. // Solid State Ionics. 2014. V. 254. P. 032. https://doi.org/10.1016/j.ssi.2013.10.032

  68. Punn R., Gameson I., Berry F. et al. // Phys. Chem. Solids. 2008. V. 69. P. 2687. https://doi.org/10.1016/j.jpcs.2008.07.003

  69. Glasser L., Jenkins H.D.B. // Chem. Soc. Rev. 2005. V. 34. P. 866. https://doi.org/10.1039/b501741f

  70. Glasser L. // Inorg. Chem. 2010. V. 49. P. 3424. https://doi.org/10.1021/ic902475n

  71. Glasser L., Jenkins H.D.B. // Inorg. Chem. 2011. V. 50. P. 8565. https://doi.org/10.1021/ic201093p

  72. Matskevich N.I., Wolf Th., Matskevich M.Yu. // J. Chem. Thermodyn. 2018. V. 118. P. 188. https://doi.org/10.1016/j.jct.2017.11.010

  73. Matskevich N.I., Shlegel V.N., Sednev A.L. et al. // J. Chem. Thermodyn. 2020. V. 143. P. 106059. https://doi.org/10.1016/j.jct.2020.106059

  74. Matskevich N.I., Semerikova A.N., Shlegel V.N. et al. // J. Alloys Compd. 2021. V. 850. P. 156683. https://doi.org/10.1016/j.jallcom.2020.156683

  75. Shannon R.D. // Acta Crystallogr. 1976. V. A32. P. 751. https://doi.org/10.1107/S0567739476001551

  76. Matskevich N.I., Wolf Th., Semerikova A.N. et al. // J. Chem. Thermodyn. 2019. V. 135. P. 143. https://doi.org/10.1016/j.jct.2019.03.034

  77. Koto K., Shulz H., Huggins R.A. // Solid State Ionics. 1980. V. 1. P. 355. https://doi.org/10.1016/0167-2738(80)90034-X

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал