Проблемы машиностроения и надежности машин, 2020, № 1, стр. 31-38

Введение. Первоначально с кавитацией связывали понижение эффективности работы устройств [1], разрушение поверхностей тел, работающих в условиях кавитации (лопастей гребных винтов судов, лопаток гидротурбин, стенок проточных каналов гидронасосов и т.д. [1–3]), шум [4] и др. В настоящее время кавитация находит широкое применение для устранения отложений на трубах теплообменных аппаратов [5], для очистки подводных объектов от морских загрязнений (в частности, от нароста ракообразных) [6], для доставки лекарств в органические клетки посредством сонопорации [7], для повышения эффективности в волновых технологиях [8, 9], используемых во многих областях хозяйственной деятельности (нефтедобыча, химия, пищевая промышленность, экология, машиностроение и т.д.).

Кавитация считается одним из основных механизмов нагрева жидкости в разнообразных технологических установках, в частности, в вихревых теплогенераторах [10, 11]. В настоящей статье рассматривается процесс нагрева жидкости при захлопывании одиночного кавитационного пузырька в неограниченном объеме неподвижной жидкости.

Постановка задачи. Изучим процесс нагрева жидкости (воды) при захлопывании в ней одиночного сферического кавитационного (парового) пузырька. Изначально (в момент времени t = 0) жидкость и пар в пузырьке покоятся, пар находится в состоянии насыщения при температуре жидкости T₀. Давление жидкости на большом удалении от пузырька постоянно и равно p_∞. Рассмотрим вариант, когда p_∞ = 10 бар, Т₀ = = 20°С, R₀ = 500 мкм. Давление жидкости p_∞ намного превышает начальное давление в пузырьке, равное давлению насыщенного пара p_S(T₀) = 0.022 бар, что и вызывает схлопывание пузырька. Такие условия коллапса могут возникать в конце расширения пузырька, образованного лазерным или искровым пробоем жидкости [12], или в конце расширения пузырька, совершающего радиальные пульсации в пучности давления стоячей волны [13]. Такие условия можно использовать также и для приближенной оценки вызываемого кавитацией нагрева жидкости в различных технологических установках [9, 10].

В общем случае процесс захлопывания кавитационного пузырька в жидкости является весьма сложным как для физического, так и для математического моделирования. В настоящей статье для его описания применим сравнительно простую физическую модель, которая учитывает ряд основных физических особенностей рассматриваемого явления. В частности, считается, что пар в пузырьке и окружающая жидкость являются теплопроводными, а на поверхности пузырька реализуется тепломассообмен. Жидкость принимается слабосжимаемой. Эффект ее сжимаемости (акустическое излучение) учитывается лишь на большом удалении от пузырька. Влияние вязкости на преобразование механической энергии в тепловую вне поверхности пузырька не учитывается. Теплоемкость жидкости полагается постоянной. Пар в пузырьке считается совершенным газом с однородным по пространству давлением (т.е. зависящим только от времени).

Математическая модель. В рамках принятых допущений математическая формулировка задачи сводится к системе дифференциальных уравнений [14] относительно скорости жидкости на поверхности пузырька ${{u}^{ + }}$, давления в пузырьке p^–, радиуса пузырька R, температуры T в пузырьке и жидкости

Здесь точка сверху означает производную по времени t; r – расстояние до центра пузырька; u – скорость; p – давление; j – скорость изменения массы при испарении/конденсации, отнесенная к единице площади; ρ – плотность; с – скорость звука; κ – коэффициент теплопроводности; нижние индексы L и ${v}$ указывают на отношение к жидкости и пару соответственно, верхние знаки + и – указывают на отношение к поверхности пузырька со стороны жидкости и пара соответственно; γ – показатель адиабаты пара; С – удельная теплоемкость жидкости. Кроме того, имеем

где σ – коэффициент поверхностного натяжения; μ – коэффициент вязкости жидкости; ${{R}_{{v}}}$ – газовая постоянная для пара; α_M – коэффициент аккомодации (испарения/конденсации); Т* – температура на поверхности пузырька; p_S(T) – давление насыщенных паров при температуре T. При температурах выше критической Т_cr различие между жидкостью и паром отсутствует. Поэтому при Т* > Т_cr массообмен на поверхности пузырька отсутствует (полагается  j = 0).

Для уравнений теплопроводности (4), (5) примем граничные условия

Здесь l(p^–) – скрытая теплота парообразования при давлении р^–.

Начальные условия (при $t = 0$) для уравнений (1)–(5) имеют вид

Учет сжимаемости жидкости в дальнем поле производится посредством слагаемых с сомножителем $c_{L}^{{ - 1}}$ в уравнении (1). Подробное изложение идеологии разбиения окружающей пузырек жидкости на ближнее поле, где жидкость считается несжимаемой, и дальнее поле, где она считается малосжимаемой, а также вывод соответствующих уравнений можно найти в [15].

В системе (1)–(5) уравнения (4), (5) описывают изменение полей температуры в паре и жидкости, соответственно. В рассматриваемой задаче они используются для расчета тонких пограничных слоев в окрестности поверхности пузырька с большими градиентами температуры, что нужно для корректного описания тепломассообмена. При отсутствии тепломассообмена уравнения (4), (5) исключаются, уравнения (2), (3) упрощаются до ${{\dot {p}}^{ - }}$ = $ - 3\gamma p\dot {R}{\text{/}}R$, $\dot {R} = {{u}^{ + }}$, а уравнение (1) превращается в известное уравнение Релея–Плессета второго порядка для радиуса адиабатического пузырька.

В рамках принятых условий имеем: ρ_L = 998.2 кг/м³, с_L = 1483 м/с, κ_L = 0.5984 Вт/(м K), ${{\kappa }_{{v}}}$ = 0.018222 Вт/(м K), γ = 1.325, С = 4150 Дж/(кг K), σ = 0.0725 Н/м, μ = 10^–3 кг/(м с), ${{R}_{{v}}}$ = 461.912 Дж/(кг K), α_M = 0.04.

Основные положения метода расчета. В методике численного решения задачи (1)–(9) [16] применяется замена переменных η = r/R, τ = t в области пузырька 0 ≤ r ≤ R и замена переменных ξ = R/r, τ = t в области жидкости R ≤ r < ∞. В результате для произвольной функции f имеем ${{f}_{t}} = {{f}_{\tau }} - \eta \frac{{\dot {R}}}{R}{{f}_{\eta }}$, ${{f}_{r}} = \frac{1}{R}{{f}_{\eta }}$, $\left. {{{f}_{r}}} \right|_{{r = R}}^{ - }$ = ${{\left. {\frac{1}{R}{{f}_{\eta }}} \right|}_{{\eta = 1}}}$ в области пузырька и ${{f}_{t}} = {{f}_{\tau }} + \xi \frac{{\dot {R}}}{R}{{f}_{\xi }}$, ${{f}_{r}} = - \frac{{{{\xi }^{2}}}}{R}{{f}_{\xi }}$, $\left. {{{f}_{r}}} \right|_{{r = R}}^{ + }$ = ${{\left. { - \frac{1}{R}{{f}_{\xi }}} \right|}_{{\xi = 1}}}$ в области жидкости. Алгоритм расчета в новых переменных основан на методе конечных разностей. При этом пространственные производные аппроксимируются центральными разностями всюду, за исключением поверхности пузырька. На поверхности пузырька используются односторонние аппроксимации, имеющие второй порядок точности. Замена пространственных производных конечными разностями сводит дифференциальные уравнения частных производных (4), (5) к системе обыкновенных дифференциальных уравнений относительно температуры T в узлах разностной сетки. Эта система оказывается связанной с обыкновенными дифференциальными уравнениями (1)–(3) относительно u⁺, $\dot {R}$ и p^– лишь посредством параметров j(T*), κ T_r|^– и l(p^–). Уравнения (1)–(3) решаются методом Дормана–Принса [17] (высокоточный вариант метода Рунге–Кутты с автоматическим выбором шага интегрирования), а указанная система относительно температуры T в узлах разностной сетки – частично неявным методом с использованием пятиточечной прогонки. Расчет ведется с применением единого временного шага, выбираемого методом Дормана–Принса. При этом на очередном временном шаге при расчете новых значений u⁺, $\dot {R}$, p^– считаются неизменными температура T^– и ее градиент $T_{r}^{ - }$ на поверхности пузырька, а при расчете нового поля температуры T в пузырьке и жидкости в качестве неизменных принимается давление p^–. В рамках рассматриваемой задачи принятая методика расчета оказалась весьма эффективной.

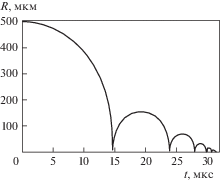
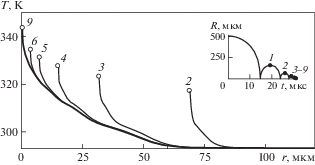
Результаты. На рис. 1 представлено уменьшение радиуса пузырька при его схлопывании. Видно, что схлопывание реализуется в виде ряда последовательно затухающих радиальных пульсаций, в результате которых пузырек довольно быстро уменьшается в размерах и исчезает. Время исчезновения пузырька можно оценить как δt ≈ ≈ ${{2{{R}_{0}}} \mathord{\left/ {\vphantom {{2{{R}_{0}}} {\sqrt {{{p}_{\infty }}{\text{/}}{{\rho }_{L}}} }}} \right. \kern-0em} {\sqrt {{{p}_{\infty }}{\text{/}}{{\rho }_{L}}} }}$ ≈ 31.6 мкс. Исчезновение пузырька обусловлено конденсацией пара на межфазной поверхности, а то, что пузырек исчезает довольно быстро, связано, главным образом, с эффектом сжимаемости жидкости.

Рисунок 2 иллюстрирует изменение температуры пара в центральной области пузырька и изменение давления пара, одинакового по всему объему пузырька. Видно, что в моменты экстремального сжатия как температура пара, так и его давление постепенно уменьшаются. В моменты же максимального расширения пузырька температура после первых двух сжатий несколько возрастает, а затем уменьшается, тогда как давление все время увеличивается.

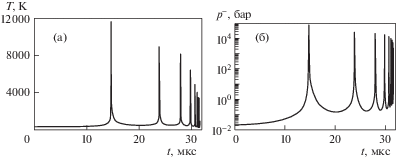
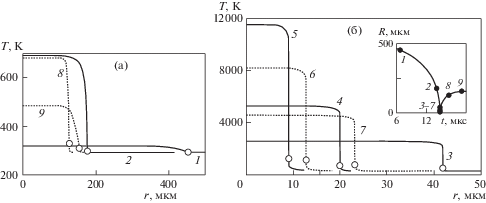
Рисунок 3 характеризует изменение температуры в пузырьке и его небольшой окрестности при первом сжатии пузырька и его последующем расширении. Видно, что в процессе сжатия температура пара в пузырьке значительно возрастает. Это обусловлено сильным и быстрым уменьшением размеров пузырька. В результате этого пар в довольно большой центральной области пузырька фактически сжимается адиабатически. Это проявляется в том, что температура в этой области почти всюду одинакова. В результате сильного повышения температура пара в пузырьке становится намного выше температуры окружающей жидкости. Вследствие этого в небольшой окрестности поверхности пузырька возникает сравнительно тонкий тепловой пограничный слой, в котором температура пара резко понижается, а температура жидкости резко возрастает. По мере сжатия температура на поверхности пузырька возрастает, что обусловлено увеличением температуры пара в результате сильного уменьшения объема пузырька.

В ходе следующего за сжатием расширения объем пузырька значительно возрастает. Это приводит к тому, что температура пара понижается. В центральной части пузырька расширение пара близко к адиабатическому. На поверхности пузырька увеличение его размеров проявляется в том, что температура на ней уменьшается.

Рисунок 4 характеризует изменение температуры в пузырьке и окружающей жидкости в моменты перехода 1–6 (указаны во вставке) от фаз расширения к фазам сжатия. Видно, что толщина слоя жидкости, в котором температура превышает начальное значение Т₀ = 293.15 K, со временем возрастает. При этом температура в пузырьке сначала (от перехода 1 к переходу 2) возрастает, а затем убывает вплоть до значений, ниже тех, что достигаются на поверхности пузырька (переходы 5, 6). По-видимому, это связано с тем, что каждое последующее сжатие начинается при больших давлениях в пузырьке (p^–, бар: 0.02 (t = 0), 0.15, 0.18, 0.20, 0.25, 0.32, 0.41, …), что приводит к понижению степени сжатия пара в пузырьке в момент локального экстремального сжатия (рис. 2).

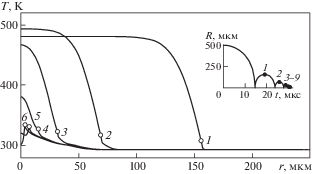
На рис. 5 представлены изменения радиальных профилей температуры жидкости в окрестности кавитационного пузырька при переходах от фаз расширения к фазам сжатия. Жирная кривая фактически представляет результат преобразования механической энергии в тепловую, реализующийся при полном исчезновении пузырька. В рассмотренном случае жидкость нагрелась в области r ≤ 60 мкм. Нагрев неоднородный. В центре он наибольший (температура достигает около 50°С), а к периферии монотонно уменьшается до нуля. Профиль температуры имеет слегка волнистый характер, что обусловлено радиальными пульсациями пузырька.

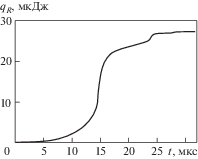
Нагрев жидкости в рамках принятой модели реализуется в результате перекачки тепловой энергии из пузырька в окружающую жидкость. Приходящую из пузырька тепловую энергию q_R можно рассчитать по формуле

здесь $\left. {{{T}_{r}}} \right|_{{r = R}}^{ + }$ – градиент температуры на поверхности пузырька со стороны жидкости.

Изменение согласно (10) тепловой энергии q_R, приходящей из пузырька в жидкость на ее нагрев в процессе схлопывания пузырька, представлено на рис. 6. Сопоставление с рис. 1 показывает, что наибольшая часть энергии поступает в жидкость в ходе первого сжатия и последующего расширения пузырька. После второго расширения прирост энергии незначителен. Это объясняется тем, что площадь поверхности, через которую реализуется теплообмен между пузырьком и жидкостью в ходе схлопывания, довольно быстро уменьшается. Согласно рис. 6, энергия q_R, поступившая на нагрев жидкости, примерно равна 27 мкДж.

Тепловую энергию ΔЕ, затраченную на нагрев жидкости в некоторой области r ≤ ${{R}_{*}}$ с радиусом ${{R}_{*}}$, можно рассчитать по профилю температуры в жидкости в конце схлопывания пузырька (жирная линия на рис. 5), воспользовавшись выражением

Согласно (11), в конце схлопывания ΔЕ = ΔЕ(R* → ∞) ≈ ΔЕ(R* = 60 мкм) ≈ 25 мкДж. Некоторое различие между результатами расчетов тепловой энергии, затраченной на нагрев жидкости при схлопывании пузырька, по формуле (10), выражающей тепловой поток через поверхность пузырька (q_R ≈ 27 мкДж), и по формуле (11), основанной на профиле температуры в конце схлопывания (ΔЕ ≈ 25 мкДж) обусловлено погрешностями вычислений.

Заключение. Представлены результаты численного исследования процесса нагрева жидкости при схлопывании одиночного кавитационного пузырька в воде при давлении жидкости p_∞ = 10 бар, ее температуре Т₀ = 20°С и начальном радиусе пузырька R₀ = 500 мкм. Применяется физическая модель, в которой пар в пузырьке и окружающая жидкость считаются теплопроводными, а на поверхности пузырька реализуется тепломассообмен. Эффект сжимаемости жидкости учитывается лишь на большом удалении от пузырька. Влияние вязкости вне поверхности пузырька на преобразование механической энергии в тепловую не учитывается. Теплоемкость жидкости полагается постоянной. Пар в пузырьке считается совершенным газом с однородным по пространству давлением (т.е. зависящим только от времени).

Показано, что в результате схлопывания пузырька в жидкости остается теплое “пятно” с радиусом r ≤ 60 мкм, т.е. примерно r < 0.1R₀. Температура жидкости в центре этого пятна приблизительно на 50°С превышает температуру жидкости Т₀. По мере удаления от центра этого пятна к периферии температура плавно уменьшается к температуре жидкости Т₀. Тепловая энергия, затраченная на нагрев жидкости в пределах этого пятна примерно равна 25 мкДж.