Проблемы машиностроения и надежности машин, 2020, № 4, стр. 11-18

Эффект транспортирования твердых и сыпучих тел по колеблющимся шероховатым поверхностям явился основой большого числа технических приложений. Теория этого эффекта сравнительно хорошо разработана для случаев, когда поверхность совершает плоскопараллельные поступательные колебания [1–6].

В настоящей статье рассматривается более сложная задача – о вибротранспортировании по шероховатой поверхности, совершающей непоступательные колебания. Такое исследование может послужить основой расширения возможностей использования вибрационной техники.

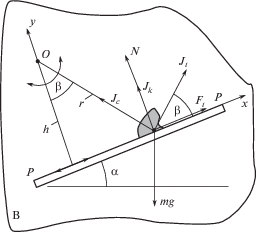
В качестве базовой модели в теории вибротранспортирования рассматривается движение плоской твердой частицы. Даже в таком виде задача приводит к существенно нелинейным “негладким” дифференциальным уравнениям, что обусловлено наличием силы сухого трения и неудерживающей связью. Основной задачей при этом является нахождение средней за период колебаний скорости движения частицы в устойчивых установившихся режимах. Более сложной является задача о вибротранспортировании по непоступательно колеблющейся поверхности. На рис. 1 представлены расчетные схемы движения частицы по поверхности, которая совершает поступательные (рис. 1а) или непоступательные (рис. 1б) колебания, связанные с поворотом поверхности относительно некоторой точки О.

На рис. 1: ($x$, $y$) – подвижная система координат, жестко связанная с вибрирующей поверхностью, $J$ – сила инерции, ${{J}_{t}}$ – тангенциальная сила инерции в относительном движении, ${{J}_{c}}$ и ${{J}_{k}}$ – центробежная и кориолисова силы инерции, $mg$ – сила тяжести, $N$ – нормальная реакция, $F$ – сила сухого трения, $\alpha $ – угол наклона поверхности к горизонту, $\beta $ – угол вибрации.

Как видно, при непоступательных колебаниях в относительном движении добавляются центробежная и кориолисова силы инерции. Кроме того, параметры, связанные с силой тяжести частицы, оказываются функциями времени.

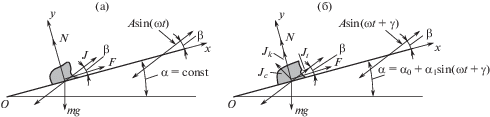
Уравнения движения. Рассмотрим движение частицы по плоскости $PP$ (рис. 2), расположенной на твердом теле В, совершающем поворотные колебания по закону

вокруг некоторого центра $О$ (${{\alpha }_{0}} = {\text{const}}$, ${{\alpha }_{1}} = {\text{const}}$).

Уравнение относительного движения частицы вдоль плоскости можно записать в виде

где ось $x$ направлена вдоль плоскости, а ось $y$ – ей перпендикулярна.

Сила сухого трения $F$, определяется соотношениями

где ${{f}_{1}}$ и $f$ – соответственно коэффициенты трения покоя и скольжения; N – нормальная реакция

Частица остается на вибрирующей поверхности при $N > 0$, т.е.

При покое частицы на плоскости ($x = {\text{const}}$) сила трения $F$ определяется из (2)

и поэтому, согласно (3), частица продолжает оставаться в покое на плоскости в любой момент времени, если $ \pm F \leqslant {{f}_{1}}N$. После преобразований последнее неравенство принимает вид

Здесь и далее верхние знаки относятся к возможным или реальным движениям частицы вперед ($\dot {x} > 0$), а нижние – назад ($\dot {x} < 0$); ${{\rho }_{1}} = \operatorname{arctg} {{f}_{1}}$.

Уравнение движения частицы по плоскости (2) при учете выражений (1), (3), (4), можно представить в форме

В этом уравнении $r$ и $\beta $ являются функциями координаты $x$ (рис. 2)

где $h = {\text{const}}$ – расстояние от центра колебаний $О$ до вибрирующей плоскости (рис. 2).

Различные возможные случаи взаимного расположения плоскости РР и центра колебаний О показаны на рис. 3, где случаи I и II соответствуют расположению точки $О$ выше плоскости и разным углам наклона вибрации, а случаи III и IV – расположению точки $О$ ниже плоскости и разным углам наклона вибрации.

Если принять, что ось $x$ всегда направлена от точки ${{О}_{1}}$ к периферии и угол вибрации $\beta $ острый (рис. 3), то в случае II в формуле (8) следует α заменить на –α, в случае III – величину x заменить на –x, а в случае IV – величину α заменить на –α и x заменить на –x.

Упрощение уравнения движения, сведение к задаче о поступательной вибрации. Уравнение (8) достаточно сложно для аналитического решения. Поэтому рассмотрим возможности упрощения решения. Заметим, что обычно величина $\dot {x}$ имеет порядок $r{{\alpha }_{1}}\omega $, а величина силы тяжести $mg$ имеет порядок тангенциальной силы инерции. Тогда величины центробежной и кориолисовой сил имеют порядок ${{\alpha }_{1}}$ по сравнению с силой тяжести и тангенциальной силой инерции. Поэтому, если амплитуда поворотных колебаний тела ${{\alpha }_{1}}$ сравнительно мала, то центробежной силой инерции и силой инерции Кориолиса можно пренебречь по сравнению с прочими силами, а уравнение (8) и формулы (4)–(7) линеаризовать относительно ${{\alpha }_{1}}$. Для случая расположения точки $О$ выше плоскости и направления оси $x$ от точки ${{О}_{1}}$ к периферии (рис 3a; случай I) уравнения (5)–(8) примут вид

Здесь $A = r{{\alpha }_{1}} = {{\alpha }_{1}}\sqrt {{{x}^{2}} + {{h}^{2}}} $; $A$ – амплитуда вибрации точки плоскости с координатой $x$.

Данное приближение вполне достаточно для приложений к задачам теории вибрационных устройств и технологий, когда ${{\alpha }_{1}}$ обычно меньше 20°. Оно достаточно и в задаче о поведении незакрепленных грузов на судах в условиях качки. Другое серьезное упрощение связано с тем, что смещение частицы за период колебаний $T = 2\pi {\text{/}}\omega $ сравнительно мало, так что при решении уравнения (9) зависимости $\beta $, $r$ и $A$ от х можно учитывать чисто параметрически, т.е. считать эти величины “локально постоянными”.

Введем обозначение $A_{ \pm }^{{{\text{eff}}}} = A\left[ {1 - \frac{g}{{r{{\omega }^{2}}}}\frac{{\cos ({{\alpha }_{0}} \pm \rho )}}{{\cos (\beta \mp \rho )}}} \right]$. Уравнение движения (9) представим в форме

Это уравнение с точностью до обозначений совпадает с соответствующим уравнением движения частицы по прямолинейно и поступательно вибрирующей плоскости [1, 2]. Поэтому для вычисления средней скорости движения частицы можно воспользоваться приведенными в указанных книгах формулами и таблицами. Существенное различие состоит только в необходимости учета зависимости $A_{ \pm }^{{{\text{eff}}}}$ от направления движения частицы от координаты $x$ (параметрически).

Параметры ${{z}_{ \pm }}$, ${{\delta }_{ \pm }}$ и ${{\gamma }_{ \pm }}$, от которых зависит скорость вибротранспортирования, вычисляются по формулам

Экспериментальные данные, сопоставление с результатами теории. Целью экспериментов была проверка некоторых основных результатов теоретических исследований. Эксперименты проводились на специальном вибрационном стенде [3], позволяющем, в частности, получать поворотные гармонические колебания рабочего стола относительно некоторой точки (центра инерции стола). Такие колебания возбуждались двумя номинально одинаковыми самосинхронизирующимися дебалансными вибровозбудителями. При вращении роторов возбудителей в одинаковом направлении имеет место устойчивый режим противофазного вращения роторов.

Экспериментальная установка представлена на рис. 4. Фанерная прямоугольная пластина 3 с размерами 900 × 260 мм и толщиной 8 мм жестко прикреплена к столу стенда. Жесткость пластины при колебаниях обеспечивалась стальными ребрами. В основной серии опытов пластина располагалась горизонтально на расстоянии $h = 175$ мм выше центра поворотных колебаний $О$, совпадающего с центром тяжести рабочего стола стенда. В качестве перемещающегося груза использован медный цилиндр диаметром 39 мм, высотой 24.5 мм, массой 241.75 г. Частота вибрации $\omega $ = 31.4 1/с (5 Гц), амплитуда угловых колебаний ${{\alpha }_{1}}$ = 1.3°. Путем измерения соответствующего угла наклона фанерной пластины с грузом было определено значение коэффициента трения $f = 0.19$.

Во время эксперимента груз первоначально размещался у края пластины и определялось перемещение груза во времени. Эта схема проведения эксперимента соответствовала случаю IV (рис. 3).

С помощью секундомера регистрировалось прохождение груза через метки на пластине, расположенные на расстояниях 5, 10, 20, 30, 40 см от оси симметрии на поверхности пластины.

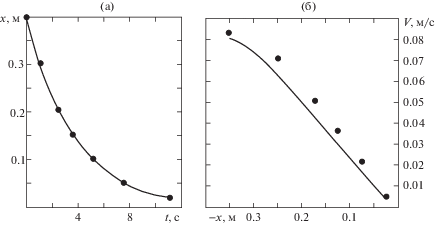
Погрешность измерений перемещения груза по пластине не превышала 5%. Результаты представлены на рис. 5а. По результатам эксперимента определена средняя скорость движения цилиндра по плоскости в различных положениях. Результаты подсчетов представлены точками на рис. 5б. Там же изображена сплошная линия, полученная путем теоретических расчетов при данных соответствующих условиям эксперимента ($f = 0.19$ мм, $h = 155$ мм, ${{\alpha }_{1}}$ = 1.3°, $A$ и $\beta $) – при соответствующих значениях координаты $x$).

При расчетах учитывалось, что при использовании самосинхронизации средний угол наклона плоскости к горизонту может несколько измениться из-за разброса параметров электродвигателей и вибраторов. На основе выполненных оценок соответствующее отклонение $\Delta {{\alpha }_{0}}$ было принято равным –5°, так что ${{\alpha }_{0}} = \Delta {{\alpha }_{0}}$ = –5°.

В пределах погрешности расчетные и экспериментальные данные совпадают.

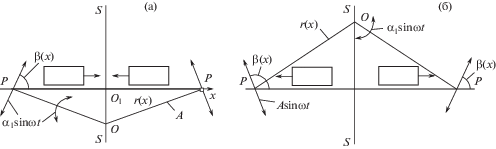
Во второй серии опытов подтверждено теоретическое заключение о зависимости направления движения частицы от взаимного расположения центра колебаний и плоскости (рис. 6). При расположении центра О ниже плоскости движение происходит от центра симметрии плоскости О₁ к ее краю с нарастающей средней скоростью, а в противном случае частица движется к центру О₁, а скорость убывает и происходит “застревание” частицы на некотором расстоянии от центра О₁. Это связано с тем, что, чем ближе частица находится от центра О₁, тем меньше угол $\beta = \operatorname{ar} с\sin (x{\text{/}}r)$ (рис. 6). При $x \approx 0$ частица либо покоится на плоскости, либо, вследствие симметрии, совершает в течение периода колебаний примерно одинаковые смещения в обоих направлениях.

Приложение к проблеме судов, перевозящих незакрепленные грузы в условиях качки. Океанские суда, перевозящие незакрепленные грузы, переворачиваются при штормовой качке. Этой проблеме в литературе уделяется значительное внимание [8–12].

Незакрепленные грузы при качке находятся в условиях, которые соответствуют нахождению на поверхности, совершающей поворотные колебания. Поведению грузов в условиях бортовой качки посвящены публикации [9–12]. В частности, в работе [10] использованы простейшие элементы изложенной теории, причем, эффективный коэффициент сухого трения при качке можно еще понизить за счет слабых высокочастотных колебательных или ударных воздействий на груз, вызванных работой корабельной машины [13].

Приложение к проблемам вибрационных технологических устройств. Особенности эффекта вибротранспортирования материала по непоступательно колеблющейся поверхности можно использовать при создании новых вибрационных процессов и технологий [2, 13]. Отметим некоторые такие особенности: 1) непоступательные, в частности, поворотные колебания обеспечивают изменение (уменьшение или увеличение) средней скорости материала по мере его продвижения вдоль вибрирующей поверхности. Это благоприятно для ряда технологических процессов; 2) поворотные колебания можно использовать для возбуждения циркулирующих потоков сыпучей среды; 3) поворотные колебания тела достаточно просто возбуждаются одним дебалансным вибратором или двумя самосинхронизирующимися вибраторами [2].

Заключение. В настоящей статье представлена задача о движении тела (частицы) по вибрирующей плоскости, совершающей непоступательные (в частности, поворотные) колебания. Эта задача представляет интерес для приложений к проблемам вибрационных технологий. Она возникает при рассмотрении особенностей поведения незакрепленных грузов на океанских судах в условиях качки. Выполненное исследование послужит толчком для усовершенствований и изобретений. Показано, что для вычисления средней скорости движения тела можно использовать известные результаты, если ввести некоторые преобразованные параметры. Приведены результаты экспериментов, согласующиеся с теоретическими данными и иллюстрирующие особенности возникающих движений.