1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 4, 2020

Проблемы машиностроения и надежности машин, 2020, № 4, стр. 19-23

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРИВОДА КЛЕТИ СКОБЫ РЕДУКЦИОННОГО СТАНА

Л. А. Чумакова *

Уральский федеральный университет имени первого Президента России Б.Н. Ельцина
Екатеринбург, Россия

* E-mail: chumakova.larisa@list.ru

Поступила в редакцию 08.02.2019
Принята к публикации 27.03.2020

Полный текст (PDF)

Аннотация

В статье рассмотрены проблемы расчета и выбора приведенной модели для изучения динамического нагружения рабочей клети скобы редукционного стана. Разработана и проанализирована расчетная схема, получена система дифференциальных уравнений для исследования динамических процессов в приводе. Изложен порядок расчета динамического нагружения, представлены формулы для расчета и приведения моментов инерции, жесткости и моментов, входящих в расчет упругих звеньев, произведено обоснование выбора расчетной динамической модели. Представлена система дифференциальных уравнений для расчета динамики нагружения привода клети скобы редукционного стана.

Ключевые слова: редукционный стан, скоба, клеть, момент инерции, расчетная динамическая модель, система дифференциальных уравнений движения масс

Редукционные станы при поштучном редуцировании в момент захвата переднего конца и при выходе заднего конца трубы испытывают повышенные динамические нагрузки. Исследованиями снижения динамических нагрузок в линии прокатных станов занимались многие ученые, однако эти процессы до настоящего времени не исследованы в полной мере [1–6]. Актуальной задачей является снижение динамических нагрузок в приводе рабочей клети скобы, повышение ее надежности и долговечности, увеличение производительности стана за счет снижения простоев, роста выпуска продукции, снижения стоимости труб.

Цель работы. Создание новой приведенной и математической модели привода клети скобы на основе многомассовой системы, испытывающей переменные нагрузки с целью снижения уровня динамической загруженности.

Методика проведения исследования. В прикладной динамике машин составление физической и математической моделей является одним из ответственных этапов, т.к. от точности определения параметров реальной машины и математического описания физических процессов зависит точность динамических расчетов [4].

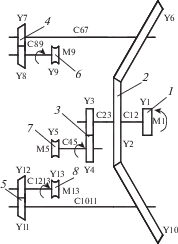
Физическая модель скобы редукционного стана с зубчатыми передачами – сложная, разветвленная система. При составлении физической модели (рис. 1) основным является обоснованный выбор минимального числа дискретных (сосредоточенных) масс, имея в виду, что сложность математического решения задачи по расчету в значительной степени возрастает с увеличением их числа.

Рис. 1.

Кинематическая схема привода клети скобы 1 – электродвигатель, 2 – тройной конический редуктор, 3 – цилиндрический редуктор, 4, 5 – двойной конический редуктор, 6, 7, 8 – прокатный валок, Y1, Y2, …, Y12 – момент инерции масс на валах, C12, C23, …, C1213 – коэффициент жесткости участков валов, M1, M2, …, M13 – внешний момент, приложенный к массам на участках валов.

Для аналитических исследований динамических явлений редукционного стана рассчитана ее эквивалентная (приведенная) модель, так что количественные и качественные результаты исследований модели с достаточной точностью (рис. 2) совпадают с результатами испытаний стана. Эффективным приемом исследования такой системы является представление ее как приведенной системы со сосредоточенными параметрами. При моделировании можно определить параметры нагружения, связанные с высоким уровнем динамических нагрузок, установить влияние зазоров в зубчатых передачах и распределение максимальных амплитуд моментов крутильных колебаний по элементам главной линии стана [4].

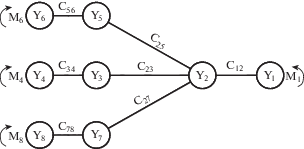
Рис. 2.

Приведенная модель привода клети скобы (расчетная схема) Y1, 2, …, Y8 – приведенные моменты инерции масс на валах, C12, C23, …, C78 – приведенные коэффициенты жесткости участков валов, M1, M2, …, M8 – приведенный внешний момент, приложенный к массам на участках валов.

Эквивалентная система скобы состоит из упругого валопровода, принимаемого как не имеющего массы, на котором располагаются сосредоточенные массы. Крутильные колебания такой системы определяются значениями моментов инерции масс относительно оси вала и крутильными жесткостями участков валопровода между ними. При составлении эквивалентной системы диаметр эквивалентного вала выбираем постоянным, а массы отдельных участков действительного вала сосредоточиваем в местах концентрации масс (муфты, зубчатые колеса).

Использование математической модели скобы в процессе проектирования позволит оценить нагруженность зубчатых передач, определить конструктивные и динамические параметры привода в целях снижения уровня динамических нагрузок.

Математическая модель скобы редукционного стана включает в себя восьми массовую механическую систему, учитывающую зазоры, параметры зубчатых передач и электропривод.

Определение приведенных инерционных масс, параметров жесткости и приведенных нагрузок для расчетной схемы (рис. 2) производится по одному алгоритму путем приведения всех звеньев привода к валу двигателя [4].

${{\left( {{{Y}_{j}}} \right)}^{k}} = {{\left( {{{Y}_{j}}} \right)}^{i}}{{\left( {\frac{{{{{\omega }}_{i}}}}{{{{{\omega }}_{k}}}}} \right)}^{2}} = {{\left( {{{Y}_{j}}} \right)}^{i}}{{u}^{2}},$
где ωi – угловая скорость i-го вала; ωk – угловая скорость k-го вала; (Yj)i – момент инерции j-й массы на i-м валу; (Yj)k – приведенный к k-му валу момент инерции j-й массы на i-м валу; u – передаточное число.
${{\left( {{{C}_{j}}} \right)}^{k}} = {{\left( {{{C}_{j}}} \right)}^{i}}{{\left( {\frac{{{{\omega }_{i}}}}{{{{\omega }_{k}}}}} \right)}^{2}} = {{\left( {{{C}_{j}}} \right)}^{i}}{{u}^{2}},$
где (Cj)i – коэффициент жесткости j-го участка i-го вала; (Cj)k – приведенный к k-му валу коэффициент жесткости j-го участка i-го вала.
${{\left( {{{M}_{j}}} \right)}^{k}} = {{\left( {{{M}_{j}}} \right)}^{i}}{{\left( {\frac{{{{{\omega }}_{i}}}}{{{{{\omega }}_{k}}}}} \right)}^{2}} = {{\left( {{{M}_{j}}} \right)}^{i}}u,$
где (Mj)i – внешний момент, приложенный к j-й массе на i-м участке; (Mj)k – приведенный к k-му валу внешний момент, действующий на j-ю массу на i-м участке.

После приведения всех звеньев привода к валу двигателя получим систему дифференциальных уравнений движущих масс, описывающую динамические процессы в приводной линии восьми массовой системы без учета затухания колебаний.

Этап приведения выглядит следующим образом:

${{Y}_{1}} = Y{\kern 1pt} {\text{1,}}$
${{Y}_{2}} = Y6{{\left( {\frac{{{\omega }67}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} + Y10{{\left( {\frac{{{\omega }1011}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} + Y2{{\left( {\frac{{{\omega }23}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\text{6}}u_{1}^{2} + Y{\text{10}}u_{2}^{2} + Y{\kern 1pt} {\text{2}}u_{3}^{2},$
${{Y}_{3}} = Y3{{\left( {\frac{{{\omega }23}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} + Y4{{\left( {\frac{{{\omega }45}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\text{3}}u_{3}^{2} + Y{\text{4}}u_{4}^{2},$
${{Y}_{4}} = Y5{{\left( {\frac{{{\omega }45}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\text{5}}u_{4}^{2},$
${{Y}_{5}} = Y7{{\left( {\frac{{{\omega }67}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} + Y8{{\left( {\frac{{{\omega }89}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\text{7}}u_{1}^{2} + Y{\text{8}}u_{5}^{2},$
${{Y}_{6}} = Y9{{\left( {\frac{{{\omega }89}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\text{9}}u_{5}^{2},$
${{Y}_{7}} = Y{\kern 1pt} 11{{\left( {\frac{{{\omega }1011}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} + Y{\kern 1pt} 12{{\left( {\frac{{{\omega }1213}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\kern 1pt} {\text{11}}u_{2}^{2} + Y{\kern 1pt} {\text{12}}u_{6}^{2},$
${{Y}_{8}} = Y{\kern 1pt} 13{{\left( {\frac{{{\omega }1213}}{{{{{\omega }}_{{12}}}}}} \right)}^{2}} = Y{\kern 1pt} {\text{13}}u_{6}^{2}.$

Результаты и обсуждения исследования. Система дифференциальных уравнений движения масс, описывающая динамические процессы в приводной линии восьмимассовой системы без учета затухания колебаний, согласно расчетной схеме имеет вид [4]

${{Y}_{1}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{1}} = {{M}_{1}} - {{C}_{{12}}}\left( {{{\Phi }_{1}} - {{\Phi }_{2}}} \right),$
${{Y}_{2}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{2}} = {{C}_{{12}}}\left( {{{\Phi }_{1}} - {{\Phi }_{2}}} \right) - {{C}_{{23}}}\left( {{{\Phi }_{2}} - {{\Phi }_{3}}} \right) - {{C}_{{25}}}\left( {{{\Phi }_{2}} - {{\Phi }_{5}}} \right) - {{C}_{{27}}}\left( {{{\Phi }_{2}} - {{\Phi }_{7}}} \right),$
${{Y}_{3}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{3}} = {{C}_{{23}}}\left( {{{\Phi }_{2}} - {{\Phi }_{3}}} \right) - {{C}_{{34}}}\left( {{{\Phi }_{3}} - {{\Phi }_{4}}} \right),$
${{Y}_{4}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{4}} = {{C}_{{34}}}\left( {{{\Phi }_{3}} - {{\Phi }_{4}}} \right) - {{M}_{4}},~$
${{Y}_{5}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{5}} = {{C}_{{25}}}\left( {{{\Phi }_{2}} - {{\Phi }_{5}}} \right) - {{C}_{{56}}}\left( {{{\Phi }_{5}} - {{\Phi }_{6}}} \right),$
${{Y}_{6}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{6}} = {{C}_{{56}}}\left( {{{\Phi }_{5}} - {{\Phi }_{6}}} \right) - {{M}_{6}},$
${{Y}_{7}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{7}} = {{C}_{{27}}}\left( {{{\Phi }_{2}} - {{\Phi }_{7}}} \right) - {{C}_{{78}}}\left( {{{\Phi }_{7}} - {{\Phi }_{8}}} \right),$
${{Y}_{8}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{8}} = {{C}_{{78}}}\left( {{{\Phi }_{7}} - {{\Phi }_{8}}} \right) - {{M}_{8}},~$
где Y1, Y2, Y3, …, Y8 – приведенные моменты инерции масс скобы, кН м с2; Φ1, Φ2, Φ3, …, Φ8 – углы поворота этих масс при колебании, рад; С12, С23, С25, С27, С34, С56, С78 – приведенные жесткости участков вала между массами, кН м/рад; М1, М4, М6, М8 – внешние моменты, приложенные к соответствующим массам систем, кН м; $~{\tau \;}$ – время, с.

Дифференциальные уравнения можно записать в более удобном для расчета виде – в форме моментов сил упругости по методу С.Н. Кожевникова. Особенностью метода С.Н. Кожевникова является то, что дифференциальные уравнения связывают внешние моменты с моментами сил упругости, а не с углами закручивания масс, как в других методах. При этом сокращается число дифференциальных уравнений в системе и решение получается в форме моментов сил упругости, что упрощает расчеты [4, 6].

После несложных преобразований, вычитая последующее уравнение из предыдущего, имея в виду что

${{M}_{{ij}}} = {{C}_{{ij}}}\left( {{{\Phi }_{i}} - {{\Phi }_{j}}} \right),\quad \frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{ij}}} = {{C}_{{ij}}}\left( {\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{i}} - \frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{\Phi }_{j}}} \right),$
получим
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{12}}} = \frac{{{{M}_{1}}}}{{{{Y}_{1}}}}{{C}_{{12}}} - {{C}_{{12}}}\frac{{{{Y}_{2}} + {{Y}_{1}}}}{{{{Y}_{1}}{{Y}_{2}}}}{{M}_{{12}}} + \frac{{{{C}_{{12}}}}}{{{{Y}_{2}}}}{{M}_{{23}}} + \frac{{{{C}_{{12}}}}}{{{{Y}_{2}}}}{{M}_{{25}}} + \frac{{{{C}_{{12}}}}}{{{{Y}_{2}}}}{{M}_{{27}}},$
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{23}}} = \frac{{{{C}_{{23}}}}}{{{{Y}_{2}}}}{{M}_{{12}}} - {{C}_{{23}}}\frac{{{{Y}_{2}} + {{Y}_{3}}}}{{{{Y}_{3}}{{Y}_{2}}}}{{M}_{{23}}} - \frac{{{{C}_{{23}}}}}{{{{Y}_{2}}}}{{M}_{{25}}} - \frac{{{{C}_{{23}}}}}{{{{Y}_{2}}}}{{M}_{{27}}} + \frac{{{{C}_{{23}}}}}{{{{Y}_{3}}}}{{M}_{{34}}},$
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{25}}} = \frac{{{{C}_{{25}}}}}{{{{Y}_{2}}}}{{M}_{{12}}} - \frac{{{{C}_{{25}}}}}{{{{Y}_{2}}}}{{M}_{{23}}} - {{C}_{{25}}}\frac{{{{Y}_{2}} + {{Y}_{5}}}}{{{{Y}_{5}}{{Y}_{2}}}}{{M}_{{25}}} - \frac{{{{C}_{{25}}}}}{{{{Y}_{2}}}}{{M}_{{27}}}~ + \frac{{{{C}_{{25}}}}}{{{{Y}_{5}}}}{{M}_{{56}}},$
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{27}}} = \frac{{{{C}_{{27}}}}}{{{{Y}_{2}}}}{{M}_{{12}}} - \frac{{{{C}_{{27}}}}}{{{{Y}_{2}}}}{{M}_{{23}}} - \frac{{{{C}_{{27}}}}}{{{{Y}_{2}}}}{{M}_{{25}}} - {{C}_{{27}}}\frac{{{{Y}_{2}} + {{Y}_{7}}}}{{{{Y}_{7}}{{Y}_{2}}}}{{M}_{{27}}} + \frac{{{{C}_{{27}}}}}{{{{Y}_{7}}}}{{M}_{{78}}},~$
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{34}}} = \frac{{{{M}_{4}}}}{{{{Y}_{4}}}}{{С}_{{34}}} + \frac{{{{C}_{{34}}}}}{{{{Y}_{3}}}}{{M}_{{23}}} - {{C}_{{34}}}\frac{{{{Y}_{5}} + {{Y}_{3}}}}{{{{Y}_{3}}{{Y}_{4}}}}{{M}_{{34}}},~$
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{56}}} = \frac{{{{M}_{6}}}}{{{{Y}_{6}}}}{{С}_{{56}}} + \frac{{{{C}_{{56}}}}}{{{{Y}_{5}}}}{{M}_{{25}}} - {{C}_{{56}}}\frac{{{{Y}_{6}} + {{Y}_{5}}}}{{{{Y}_{5}}{{Y}_{6}}}}{{M}_{{56}}},~$
$\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{M}_{{78}}} = \frac{{{{M}_{8}}}}{{{{Y}_{8}}}}{{С}_{{78}}} + \frac{{{{C}_{{78}}}}}{{{{Y}_{7}}}}{{M}_{{27}}} - {{C}_{{78}}}\frac{{{{Y}_{8}} + {{Y}_{7}}}}{{{{Y}_{7}}{{Y}_{8}}}}{{M}_{{78}}},~$
где ${{M}_{{ij}}} = {{C}_{{ij}}}\left( {{{\Phi }_{i}} - {{\Phi }_{j}}} \right)~$ – моменты сил упругости на участке линии передачи между i-й и j-й массами.

При рассмотрении взаимного влияния всех входящих в расчет величин на стадии приведения значительно упрощается расчет, приводящий к существенному уменьшению количества дифференциальных уравнений в системе. При этом учитываются влияние всех масс приводной линии клети скобы на конечный результат.

Выводы. Выполненная на основе приведенных зависимостей математическая модель клети скобы позволяет оценить характер динамического нагружения, что повысит работоспособность привода путем выбора рациональных параметров звеньев, которые обеспечивают наименьший уровень динамических усилий без потери жесткости приводной линии клети.

Полученная математическая модель является составной частью, разработанной на кафедре “Металлургические и роторные машины” методики, позволяющей проводить технологические расчеты и связанные с ними расчеты динамического нагружения для оценки работоспособности и выбора рациональных параметров звеньев. Проведенные расчеты в выполненной математической модели были использованы для разработки рабочей клети редукционного стана.

Список литературы

  1. Chumakova L.A. Influence of Rolling Torques on the Dynamic Loads in Mill Drives // Russian Engineering Research. 2019. V. 39. № 10. P. 852.

  2. Malafeev S.I., Malafeeva A.A., Konyashin V.I. Correction of Rolling Mill Mechatronic System to Limit Dynamic Loads // Russian Engineering Research. 2018. V. 38. № 10. P. 431.

  3. Chechulin Y.B., Popov Y.A. Minimizing the dynamic loads in pilger rolling mill forholler // Solid State Phenomena. 2017. V. 265. P. 1034.

  4. Чумакова Л.А. Исследование условий работы и режимов динамического нагружения редукционного стана ТПА 30-102 с целью повышения надежности рабочей клети: дис. … канд. техн. наук. Екатеринбург, 2006. 150 с.

  5. Khramshin V.R., Karandaev A.S., Evdokimov S.A., Andryushin I.Y., Shubin A.G., Gostev A.N. Reduction of the dynamic loads in the universal stands of a rolling mill // Metallurgist. 2015. V. 59. P. 3.

  6. Иванченко Ф.К. Динамика металлургических машин / Под ред. Ф.К. Иванченко, В.А. Красношапка. М.: Металлургия, 1983. 295 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал