Проблемы машиностроения и надежности машин, 2020, № 6, стр. 35-47
Моделирование взаимодействия оператора и экзоскелета
С. Ф. Яцун 1, *, А. С. Яцун 1, Е. В. Савельева 1, А. Е. Карлов 1
1 Юго-Западный государственный университет
Курск, Россия
* E-mail: teormeh@inbox.ru
Поступила в редакцию 21.05.2020
Принята к публикации 29.07.2020
Аннотация
В статье рассмотрена структура аппаратных средств человеко-машинного интерфейса промышленных экзоскелетов и соответствующие математические модели, позволяющие подобрать оптимальные параметры человеко-машинного интерфейса и разработать алгоритмы управления. Предложен четырехэтапный алгоритм планирования угла поворота спины оператора при выполнении операции по подъему груза на основании полиномов седьмого порядка. Выполнено моделирование движения системы человек–экзоскелет с акцентом на тазобедренный сустав и поясничный отдел позвоночника. Показано влияние параметров математической модели системы человек–экзоскелет и в том числе мышечной системы оператора на точность воспроизведения экзоскелетом движений оператора.
Появление экзоскелетов облегчает труд работников промышленной сферы, улучшая условия труда и открывая новые функциональные возможности оператора при выполнении технологических операций, связанных с подъемом и переносом грузов [1–4]. В настоящее время передовые версии промышленных экзоскелетов позволяют выполнять операции с грузами до 60 кг. Их применение в промышленной отрасли облегчает тяжелый физический труд работников предприятий и при этом сокращает риск появления производственного травматизма. Функционирование экзоскелета необходимо рассматривать как систему, в которой человек и экзоскелет (ЧЭ) связаны между собой человеко-машинным интерфейсом (ЧМИ), охватывающим различные аспекты взаимодействия между элементами системы, который состоит не только из технических средств, но и соответствующего программного обеспечения. ЧМИ является важным компонентом системы, обеспечивая эффективность, гибкость функционирования системы ЧЭ. Методы проектирования системы ЧЭ связаны с разработкой инструментальных средств виртуального проектирования на основе математического моделирования взаимодействия человека и экзоскелета. Несмотря на рост публикаций по этой тематике, вопросы моделирования поведения системы ЧЭ изучены недостаточно, и требуют дальнейшего развития [5], особенно, когда речь идет о силовом взаимодействии, которым характеризуются системы ЧЭ [6–12]. В статье, разрабатываются математические модели элементов системы, обсуждаются вопросы персонификации ЧМИ, который ассоциируется с измерением и обработкой сигналов, регистрирующих силовое и кинематическое взаимодействие в системе. Одной из основных задач, решаемых интерфейсом, является создание наилучших условий кооперативного поведения системы ЧЭ. Наиболее эффективно с такой задачей справляется интерфейс, который обладает совокупностью свойств, в том числе таких как: способность оценивать состояние окружающей среды, взаимодействие человека и экзоскелета, формирование управляющих сигналов, а также своевременное реагирование на изменения, происходящие в системе ЧЭ.
Описание системы человек–экзоскелет. Будем рассматривать систему человек–экзоскелет, которая представляет собой сложную био-электро-механическую многозвенную систему, математическая модель которой представляет собой систему нестационарных нелинейных дифференциальных уравнений. При проектировании экзоскелетных систем можно применять механизмы параллельной структуры, что накладывает свой отпечаток на моделирование движений системы такого строения [13, 14].
На данном этапе, ограничимся рассмотрением движения спины оператора и экзоскелета относительно тазобедренного сустава (ТБС).
В рассматриваемой системе, оператор осуществляет информационное взаимодействие с окружающей средой с помощью зрения, тактильных сенсоров и силовое взаимодействие за счет мышечной системы ТБС, человеко-машинный интерфейс, контролирующий силовое и информационное взаимодействие человека с экзоскелетом и, собственно, экзоскелет, создающий дополнительные силовые воздействия на оператора, что обеспечивает снижение нагрузки на мышечную систему оператора. Экзоскелет снабжен системой персонифицированных фиксирующих элементов, гарантирующих комфортное пребывание оператора в экзоскелете.
На рис. 1 представлена схема системы человек–экзоскелет. Здесь обозначены элементы экзоскелета: 3 – бедро; 4 – спина и звенья оператора: 5 – спина; 6 – бедро; 7 – рука и 8 – груз.
Сi – центры масс звеньев системы; M34 – моменты, создаваемые электроприводами шарниров; Д34 – датчик угла поворота звена 4 относительно звена 3; Д3 – датчик абсолютного угла наклона звена; R80 – реакция поверхности при начальном положении груза; $\bar {F}$ – сила, действующая на руку оператора со стороны груза; $\bar {G}$ – вес груза.
Положение звеньев экзоскелета и оператора оценивается абсолютными углами φ3, φ4, φ5. Для контроля над этими углами применяются датчики углов поворота Д3, Д4, Д5. Взаимодействие спины оператора и спины экзоскелета измеряется с помощью датчика силы ${{\bar {P}}_{{54}}}$. Взаимодействие груза с опорной поверхностью контролируется датчиком силы ${{\bar {R}}_{{80}}}$, а взаимодействие оператора с грузом оценивается датчиком силы $\bar {F}$; $\bar {G}$ – вес груза.
Человек оценивает окружающую среду и воздействует на технологическую нагрузку (груз), создавая мышечной системой моменты, действующие в ТБС. Экзоскелет, оснащенный электроприводами, создающими моменты относительно тазобедренного шарнира (ТБШ), помогает оператору выполнять ту или иную технологическую операцию, значительно снижая уровень моментов мышечной системы, а в ряде случаев полностью разгружая человека [15–18].
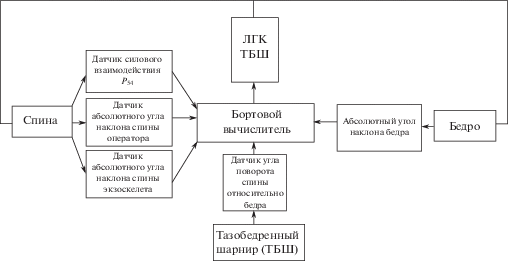
Структура ЧМИ приведена на рис. 2. Этот интерфейс, контролирующий как силовые, так и кинематические параметры системы состоит из модулей спины, бедра, ТБШ, и управляемого устройства, установленного в ТБШ, получившего название линейный гравитационный компенсатор (ЛГК).
Мерой силового взаимодействия в системе ЧЭ является сила ${{P}_{{54}}}$, которая измеряется специальным датчиком. Также интерфейс имеет информационные каналы, с помощью которых, происходит измерение углов поворота звеньев оператора и экзоскелета. Бортовой вычислитель обрабатывает эту информацию в соответствии с алгоритмом управления и формирует управляющее напряжение, поступающее на ЛГК ТБШ, который воздействует на экзоскелет, задавая характер желаемых движений звеньев экзоскелета.
На данном этапе исследований предположим, что оси вращения ТБШ и ТБС совпадают. Кроме того, примем, что бедренное звено экзоскелета жестко связано с бедром оператора [19–21].
Планирование желаемой траектории движения. Предположим, что планируемый закон изменения угла наклона спины оператора $\varphi _{5}^{*}$ является гладкой функцией, которая, как и ее первая и вторая производные, не имеет разрывов в начальный и конечный моменты движения [22]. Такую функцию можно представить в виде комбинации отрезков прямой и полиномов седьмого порядка. Будем считать, что общее время подъема груза состоит из четырех отдельных этапов
где t1 – время подготовки; t2 – выполнения наклона; t3 – фиксации спины в положении наклона и t4 – подъема спины.Коэффициенты ${{c}_{i}}$ находятся из соответствующих граничных условий как решение алгебраического уравнения
где ${{A}_{1}}$, ${{B}_{1}}$ – матрицы граничных условий, $C$ – матрица коэффициентов ${{c}_{i}}$.Коэффициенты ${{d}_{i}}$ находятся из соответствующих граничных условий как решение алгебраического уравнения
где ${{A}_{2}}$, ${{B}_{2}}$ – матрицы граничных условий; $D$ – матрица коэффициентов ${{d}_{i}}$.Для построения траектории движения приняты следующие значения функции и ее производных на границах соответствующих интервалов
(4)
$\begin{gathered} \dot {\varphi }_{5}^{*}({{t}_{1}}) = \dot {\varphi }_{{50}}^{*};\quad \dot {\varphi }_{5}^{*}({{t}_{2}}) = \dot {\varphi }_{{5\max }}^{*};\quad \dot {\varphi }_{5}^{*}({{t}_{3}}) = \dot {\varphi }_{{5\max }}^{*};\quad \dot {\varphi }_{5}^{*}({{t}_{4}}) = 0, \\ \ddot {\varphi }_{5}^{*}({{t}_{1}}) = \varphi _{{50}}^{*};\quad \ddot {\varphi }_{5}^{*}({{t}_{2}}) = \ddot {\varphi }_{{5\max }}^{*};\quad \ddot {\varphi }_{5}^{*}({{t}_{3}}) = \varphi _{{5\max }}^{*};\quad \ddot {\varphi }_{5}^{*}({{t}_{4}}) = 0, \\ \end{gathered} $Интервалы времени определены как ${{t}_{1}} = 1$; ${{t}_{2}} = 2$; ${{t}_{3}} = 3$; ${{t}_{4}} = 4$ с. Интервалы времени 1–2 и 3–4 соответствуют процессу подъема и опускания груза. На интервале 2–3 с происходит удержание груза. В этот период желаемый угол наклона спины оператора по отношению к бедру остается неизменным.
Модели сил, приложенных к системе. Рассмотрим математические модели сил, приложенных к системе ЧЭ. Момент веса звена ${{\bar {G}}_{i}}$ относительно центра ТБШ ${{O}_{{43}}}$ определим в виде
(5)
${{\bar {M}}_{{{{o}_{{43}}}}}}(\bar {G}) = \bar {r}_{{_{{{{O}_{{43}}}{{C}_{i}}}}}}^{{(0)}} \times \bar {G}.$Суммарный момент сил веса
(6)
${{\bar {M}}_{5}} = \sum {\bar {r}_{{_{{{{O}_{{43}}}{{C}_{i}}}}}}^{{(0)}} \times {{{\bar {G}}}_{i}}} ,$Модуль момента сил веса относительно О43 представим в виде
(8)
${{M}_{5}}(t) = {{L}_{5}}{{m}_{5}}g\sin {{\varphi }_{5}} + ({{L}_{8}}\sin {{\varphi }_{8}} + {{L}_{5}}\sin {{\varphi }_{5}}) \cdot ({{\delta }_{2}}(t - {{t}_{2}}){{m}_{8}}g - {{\delta }_{1}}(t - {{t}_{2}}){{N}_{{80}}}),$На интервале ${{t}_{2}} \leqslant t \leqslant {{t}_{3}}$ груз остается неподвижным, а реакция ${{N}_{{80}}}$ уменьшается до 0. При выполнении условия ${{N}_{{80}}} = 0$ завершается отрыв груза и начинается следующий этап – подъем груза.
Обычно, значение веса груза известно с определенной погрешностью. Такая неопределенность ограничивается интервалом, заданным максимально и минимально возможными значениями параметра, в пределах которого этот параметр может изменяться. Т.е. ${{G}_{i}} = {{G}_{{i0}}} + \Delta {{G}_{i}}$, где ${{G}_{{i0}}}$ – медианное значение веса i-го звена; $\Delta {{G}_{i}}$ – интервал изменения веса. Примем для веса груза ${{G}_{{80}}} = {{m}_{8}}g$, а $\Delta {{G}_{8}} = \Delta {{m}_{8}}g$.
Для моделирования измерителя силы ${{P}_{{54}}}$, возникающей между спиной экзоскелета и спиной оператора, принята линейная упруго-вязкая модель Кельвина–Фойхта с параметрами C54, ${{\mu }_{{54}}}$. Модуль этой силы определим по формуле
(9)
${{P}_{{54}}} = {{C}_{{54}}}({{\varphi }_{5}} - {{\varphi }_{4}}) + {{\mu }_{{54}}}({{\dot {\varphi }}_{5}} - {{\dot {\varphi }}_{4}}).$Момент силы измерителя относительно точки О43
Для построения математической модели момента, создаваемого мышечной системой бедренного сустава человека, будем считать, что момент мышечной системы тазобедренного сустава зависит от отклонения реального угла наклона спины от желаемого.
Наиболее известной моделью мышц является модель Хилла [15]. Уравнение Хилла является основным уравнением динамики мышечного сокращения и описывает взаимосвязь между силой и скоростью укорочения
Здесь Р – сила; V – скорость, которые развивает мышца; a, b, Pm – постоянные величины. Из этого равенства следует вывод, что между силой и скоростью существует обратно пропорциональная зависимость. Если скорость V = 0, то подстановка этого значения приводит к соотношению P = Pm, т.е. в этом случае мышца развивает максимальную силу, равную Pm. Если сила сокращения равна нулю, скорость достигает максимальной величины.
Далее сделано предположение о том, что реальный угол ${{\varphi }_{5}}(t)$ наклона спины оператора отличается на некоторую величину от желаемого $\varphi _{5}^{*}(t)$ и момент, мышц зависит от разности между желаемым и реальным углами, а также предполагается, что с ростом числа циклов нагружения, сила, создаваемая мышечной системой, уменьшается.
В статье, принята математическая модель мышечной системы ТБШ в виде
(13)
$M_{5}^{{\text{Ч}}} = {{K}_{p}}(\varphi _{5}^{*} - {{\varphi }_{5}}) + {{K}_{d}}(\dot {\varphi }_{5}^{*} - {{\dot {\varphi }}_{5}}),$(14)
${{K}_{р}}(n) = \frac{{{{K}_{{ро}}}}}{{с - n}},\quad {{K}_{d}}(n) = \frac{{{{K}_{{dо}}}}}{{d - n}},$Сила, создаваемая ЛГК ТБШ, является управляющей и определяется по формуле
${{\Phi }_{1}}$ – сила, создаваемая упругим элементом ЛГК где $С$ – коэффициент, определяемый свойствами упругого элемента; $\Delta L$ – изменение длины ЛГК.${{\Phi }_{2}}$ – сила, создаваемая электроприводом ЛГК, реализованным на основе ШВП
где ${{М}_{В}}$ – момент электропривода, приведенный к гайке ШВП, $h$ – шаг винта ШВП.В свою очередь
где ${{М}_{{{\text{эд}}}}}$ – момент электродвигателя; ${{\eta }_{р}}$ – передаточное отношение гайка-шестерня; $\eta $ – передаточное отношение редуктора. Момент, создаваемый электродвигателем где i – ток в обмотках электродвигателя ЛГК; cM – постоянная момента электродвигателя.Ток i определим из уравнения полного тока
где L, R – индуктивность и активное сопротивление обмотки ротора; сЕ – коэффициент пропорциональности, называемый постоянной ЭДС двигателя; $\dot {\varphi }$ – угловая скорость ротора электродвигателя; U – управляющее напряжение.Момент силы $\Phi $, создаваемый относительно оси вращения ТБШ определим по формуле
где ${{O}_{{43}}}H$ – плечо силы $\Phi $ относительно центра ТБШ.Математическая модель системы ЧЭ. Математическую модель функционирования системы ЧЭ можно описать с помощью нелинейного матричного уравнения, имеющего вид
где $\bar {X} = {{({{\varphi }_{4}},{{\omega }_{4}},{{\varphi }_{5}},{{\omega }_{5}})}^{T}}$; ${{\omega }_{4}} = {{\dot {\varphi }}_{4}}$; ${{\omega }_{5}} = {{\dot {\varphi }}_{5}}$;управляющее воздействие
Алгоритм управления. Система управления должна рассматриваться как робастная, т.е. обеспечивающая допустимое (в смысле некоторого критерия) качество при наличии параметрических и функциональных неопределенностей объекта управления, связанных с недостаточной информацией о весе поднимаемого груза [12, 19]. Принято, что в ходе функционирования системы, коэффициенты регулятора не подстраиваются, а малая чувствительность (т.е. робастность) к различного рода вариациям параметров математической модели объекта достигается за счет специальным образом выбранной структуры алгоритма управления.
В нелинейных робастных системах малая чувствительность к различным вариациям математической модели объекта управления обеспечивается за счет дополнительного введения в алгоритм управления специальной статической нелинейной обратной связи.
Представим алгоритм управления в виде
(24)
${{f}_{1}}({{P}_{{54}}}) = \left\{ {\begin{array}{*{20}{l}} {0{{P}_{{540}}} < {{P}_{{54}}} < {{P}_{{541}}},} \\ {\Delta {{U}_{1}}{{P}_{{540}}} > {{P}_{{54}}},} \\ { - \Delta {{U}_{1}}{{P}_{{54}}} > {{P}_{{541}}};} \end{array}} \right.$Для рассматриваемой системы выбран ПД регулятор
где Ku, Kdu – коэффициенты регулятора; $\Delta \varphi = \varphi _{5}^{*} - {{\varphi }_{4}}$.Параметры Ku, Kdu определяются исходя из критерия качества переходного процесса системы. Подставляя необходимые параметры в (24) получим уравнение адаптивного регулятора
(26)
${{U}_{1}} = {{k}_{1}}\Delta \varphi + {{k}_{2}}\Delta \dot {\varphi } + {{f}_{1}}({{P}_{{54}}}) + {{f}_{2}}({{\varphi }_{{43}}}).$Такой регулятор создает управляющее напряжение ${{U}_{1}}$ с учетом уровня параметров ${{P}_{{54}}}$ и ${{\varphi }_{{43}}}$, обеспечивая их значения в заданном интервале.
Результаты математического моделирования работы системы управления БШТС. Далее методом математического моделирования исследуется влияние параметров модели на характер функционирования ЧЭ. Кинематические особенности поведения системы отражены на диаграммах в виде зависимостей углов поворота спины оператора и экзоскелета углов φ4, φ5, φ5* от времени на всем интервале движения системы при подъеме груза. Силовые возможности ЛГК ТБШ иллюстрируются графиками зависимости сил Φ1 и Φ2, создаваемых упругим элементом и электроприводом ЛГК на всем интервале движения системы при подъеме груза. Возможности мышечной системы и нагрузки на эту систему отражены на графиках в виде зависимостей момента мышечной системы оператора $M_{5}^{{\text{Ч}}}$ от времени.
При расчетах приняты следующие неизменяемые параметры модели: m5 = 35 (кг) – масса туловища оператора; m4 = 12 (кг) – масса спины экзоскелета; m8 = 30 (кг) – масса поднимаемого груза; I5 = 3.365 (кг м2) – момент инерции тела оператора; I4 = 1 (кг м2) – момент инерции экзоскелета.
Моделирование функционирования системы ЧЭ выполнено при различных варьируемых параметрах модели. Параметры регулятора системы управления электроприводом ЛГК: Ku = 10 В – пропорциональный; Kdu = 0.5 В/с – дифференциальный.
Феноменологические параметры мышечной системы человека: Kp = 1000 Н·м – упругие свойства мышечной системы; Kd = 100 Н·м·с – диссипативные свойства мышечной системы.
Параметры измерителя силы: С54 = 1000 Н/м – упругие свойства; ${{\mu }_{{54}}}$ = 10 Н с/м – диссипативные свойства.
Жесткость упругого элемента ЛГК: С = 7000 Н/м.
Для анализа отклонения реальных углов наклона от заданных исследуются три области, отмеченные на графике рис. 3а цифрами 1, 2, 3. Область 1 соответствует режиму наклона спины без груза; область 2 – отрыву груза от поверхности; область 3 – подъему груза.
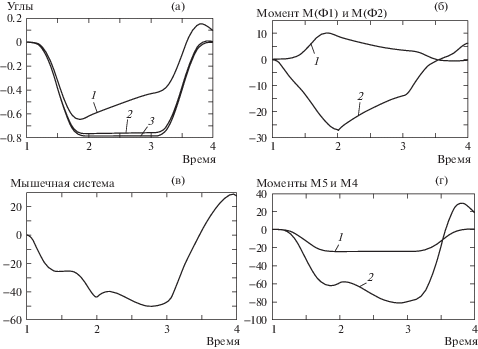
Рис. 3.
Зависимости исследуемых параметров от времени: (а) – зависимость углов поворота спины оператора и экзоскелета углов φ4, φ5, φ5* от времени на всем интервале движения системы при подъеме груза; (б) – зависимость моментов сил Φ1 и Φ2, создаваемых ЛГК на всем интервале движения системы при подъеме груза; (в) – зависимость момента мышечной системы оператора $M_{{\text{5}}}^{{\text{ч}}}$ от времени; (г) – зависимость моментов сил тяжести М5 и М4: 1 – М4; 2 – М5.
Феноменологические параметры мышечной системы человека Kр, Kd отражают упругие и диссипативные свойства мышечной системы, которые определяют степень подготовленности мышечной системы к подъему груза.
Результаты расчетов, выполненных при параметрах Kр = 1000 Н·м и Kd = 100 Н·м·с приведены на рис. 3а показывают значительное отклонение угла поворота спины экзоскелета от заданного, которое достигает максимума равного $\Delta \varphi $ = 0.2 радиана в зоне 2.
Далее приведены зависимости моментов сил Φ1 и Φ2 от времени, показывающие как происходит изменение моментов сил, генерируемых ЛГК (рис. 3б). Момент силы упругого элемента Φ1 достигает максимальных значений 10 Н·м на первом этапе и далее на этапе отрыва груза от поверхности снижается, на третьем этапе, уменьшается до нуля. Момент силы Φ2, генерируемой электроприводом принимает максимальное значение 27 Н·м в конце первого этапа далее уменьшается до нуля.
Зависимость момента мышечной системы оператора $M_{5}^{{\text{ч}}}$ от времени (рис. 3в) показывает вклад оператора в процесс подъема груза. Максимальное значение $M_{5}^{{\text{ч}}}$ достигает в конце этапа, связанного с отрывом груза от поверхности, при этом $M_{5}^{{\text{ч}}} = 50$ Н·м. Далее происходит уменьшение этого момента до нуля с последующей инвертацией.
Зависимость момента измерителя силы ${{Р}_{{54}}}$ от времени (рис. 4а) показывает монотонный рост момента, который достигает максимума $М({{Р}_{{54}}})$ = 34 Н·м в конце второго этапа при $t = 3$ с.
Рис. 4.
Зависимости исследуемых параметров от времени: (а) – момента измерителя силы ${{Р}_{{54}}}$ от времени; (б) – углов поворота спины оператора и экзоскелета углов φ4, φ5, φ5* от времени на всем интервале движения системы при подъеме груза: 1 – φ4; 2 – φ5; 3 – φ5*; (в) – моментов сил Φ1 и Φ2, создаваемых ЛГК на всем интервале движения системы при подъеме груза; (г) – момента мышечной системы оператора $M_{5}^{{\text{ч}}}$ от времени; (д) – моментов сил тяжести М5 и М4: 1 – М4; 2 – М5; (е) – момента измерителя силы ${{Р}_{{54}}}$ от времени.
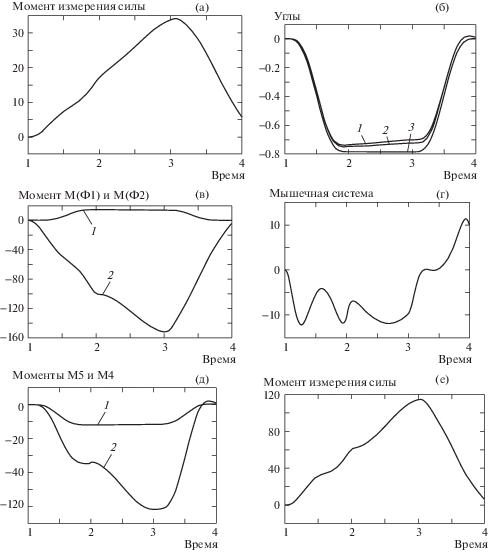
Для уменьшения погрешности угла поворота экзоскелета предложено изменить жесткость измерителя силы до С54 = 5000, сохранив неизменными остальные параметры системы. На рис. 4б показаны диаграммы зависимостей углов поворота спины оператора и экзоскелета φ4, φ5, φ5* от времени. Максимальное отклонение по углу поворота спины оператора от желаемого равна 0.06 рад, а для экзоскелета – 0.09 рад.
Зависимости моментов сил Φ1 и Φ2 от времени (рис. 4в), показывают что момент силы упругого элемента Φ1 достигает максимальных значений 22 Н·м на первом этапе и далее на этапе отрыва груза от поверхности остается неизменным, на третьем этапе, при подъеме груза снижается до нуля. Момент силы Φ2, генерируемой электроприводом принимает максимальное значение 150 Н·м в конце второго этапа, связанного с отрывом груза от поверхности, и далее уменьшается до нуля.
Зависимость момента мышечной системы оператора $M_{5}^{{\text{ч}}}$ от времени (рис. 4г) показывает немонотонный характер, а максимальное значение $M_{5}^{{\text{ч}}}$ достигает в конце этапа, связанного с отрывом груза от поверхности, при этом $M_{5}^{{\text{ч}}} = 12$ Н·м. Далее происходит уменьшение этого момента до нуля с последующей инвертацией. Таким образом, удалось снизить нагрузку на оператора, уменьшив момент $M_{5}^{{\text{ч}}}$ более чем в четыре раза.
Зависимость момента измерителя силы ${{Р}_{{54}}}$ от времени (рис. 4е) как и в предыдущем случае показывает монотонный рост момента, который достигает максимума $М({{Р}_{{54}}})$ = 115 Н·м в конце второго этапа при t = 3 с, что превышает момент $М({{Р}_{{54}}})$ в предыдущем примере более чем в три раза.
Заключение. В статье предложена структура аппаратных средств ЧМИ и соответствующие математические модели, позволяющие подобрать оптимальные параметры ЧМИ и разработать алгоритмы управления. Предложен четырехэтапный алгоритм планирования угла поворота спины оператора при выполнении операции по подъему груза на основании полиномов седьмого порядка. Выполнено моделирование движения системы ЧЭ. Показано влияние параметров математической модели системы ЧЭ и, в том числе, жесткости измерителя силы на точность воспроизведения экзоскелетом движений оператора. Приводится математическое описание планирования желаемой траектории движения звеньев, смоделированы силы, действующие на систему, математически описана сама система и алгоритм управления.
Анализ полученных диаграмм показал, что реальный угол наклона спины оператора φ5, отличается от виртуального желаемого угла $\varphi _{5}^{*}(t)$, а в зависимости от величины феноменологического параметра упругих свойств мышечной системы человека. Также наблюдается отклонение угла наклона спины экзоскелета φ4 от φ5, которое определяется моментом, создаваемой измерителем силы.
Графики ассистирующего момента M(P54), действующий на оператора со стороны экзоскелета показывают то, что момент силы P54 синхронно без запаздывания формируется измерителем силы.
Установлено, что погрешность реальных движений по отношению к задуманным существенно зависит от коэффициента жесткости измерителя силы C54. Это хорошо видно при сравнении диаграмм углов φ5 и φ5* .
Проведенные исследования также показали работоспособность моделей и возможность прогнозирования характера поведения системы человек–экзоскелет при выполнении движений, связанных с подъемом груза.
Список литературы
Ergasheva B.I. Lower Limb Exoskeletons: Brief Review // Научно-технический вестник информационных технологий, механики и оптики. 2017. Т. 17. № 6. С. 1153.
De Looze M.P., Bosch T., Krause F., Stadler K.S., & O’Sullivan, L.W. Exoskeletons for industrial application and their potential effects on physical work load. Ergonomics, 2016. V. 59 (5). P. 671.
Spada S. et al. Analysis of exoskeleton introduction in industrial reality: main issues and EAWS risk assessment // International Conference on Applied Human Factors and Ergonomics. Springer. Cham. 2017. P. 236.
Яцун С.Ф., Антипов В.М., Карлов А.Е. Подъем груза в экзоскелете с гравитационной компенсацией / Под ред. С.Ф. Яцун, В.М. Антипов, А.Е. Карлов, Аль Манджи Х.Х.М. // Известия Юго-Западного государственного университета. 2019. Т. 23. № 2. С. 8.
Гаврилов С.В., До Т.З. Компьютерное моделирование динамики движения пятистепенного шагающего робота // Автоматизация в электроэнергетике и электротехнике. 2016. V. 1. P. 72.
Plagenhoef, Stanley, F. Gaynor Evans, Thomas Abdelnour. Anatomical data for analyzing human motion. // Research quarterly for exercise and sport 54. 1983. № 2. P. 169.
Theurel J., Desbrosses K., Roux T., Savescu A. Physiological consequences of using an upper limb exoskeleton during manual handling tasks // Applied ergonomics, 2018. V. 67. P. 211.
Ulrey B.L., Fathallah F.A. Subject-specific, whole-body models of the stooped posture with a personal weight transfer device // Journal of Electromyography and Kinesiology. 2013. V. 23. № 1. P. 206.
Герасимов Д.Н., Лызлова М.В., Никифоров В.О. Простые алгоритмы адаптивного и робастного управления классом линейных объектов с переменными параметрами // Известия высших учебных заведений. Приборостроение. 2015. Т. 58. № 5. С. 351.
Гурьев В.Ю. Математическое моделирование биомеханических процессов в неоднородном миокарде: Дис…. канд. физ.-мат. наук. Урал. ун-т. 2004.
Домрачев Т.Б., Яшметов К.С., Лоскутов Ю.В. Кинематика локомоций человека при вставании из седа и посадке на опору // Инженерные кадры – будущее инновационной экономики России. 2017. № 1. С. 40.
Лавровский Э.К. Об энергетике походок человека-оператора, осуществляемых при помощи аппарата “Пассивный” экзоскелетон // Известия Российской академии наук. Механика твердого тела. 2015. № 1. С. 9.
Алешин А.К., Глазунов В.А., Оффер Ш., Рашоян Г.В., Скворцов С.А., Ласточкин А.Б. Анализ элементарных перемещений манипулятора параллельной структуры с круговой направляющей на основе дифференцирования уравнений связей // Проблемы машиностроения и надежности машин. 2016. № 5. С. 17.
Глазунов В.А. и др. Разработка механизмов параллельной структуры с четырьмя степенями свободы и частичной развязкой // Проблемы машиностроения и надежности машин. 2010. № 5. С. 3.
Jatsun S., Savin S., Lushnikov B., Yatsun A. System analysis of sagittal plane human motion wearing an exoskeleton using marker technology / In ITM Web of Conferences. 2016. V. 6. EDP Sciences.
Jatsun S.F., Al Maji Kh.M. Analysis of the effect of the exoskeleton geometrical dimensions on the nature of a linear compensator operation / S.F. Jatsun, Al Maji Kh.M., A.S. Yatsun, A.E. Karlov, E.V. Saveleva // Developments in eSystems Engineering 2019. Robotics, Sensors and Industry.
Борисов А.В., Розенблат Г.М. Матричный метод составления дифференциальных уравнений движения экзоскелета и управление им // ПММ. 2017. Т. 81. № 5. С. 511.
Павловский В.Е. и др. Биомехатронный комплекс нейрореабилитации – концепция, конструкция, модели и управление // Препринты Института прикладной математики им. М.В. Келдыша РАН. 2014. № 0. С. 111.
Борисов А.В. Механика пространственной модели экзоскелета и антропоморфного робота // Вопросы оборонной техники. Серия 16: Технические средства противодействия терроризму. 2018. № 3–4. С. 46.
Гаврилов С.В., До Т.З. Компьютерное моделирование динамики движения пятистепенного шагающего робота // Автоматизация в электроэнергетике и электротехнике. 2016. № 1. С. 72.
Яцун С.Ф. и др. Моделирование паттернов походки пациента с повреждением опорно-двигательного аппарата с помощью экзоскелета // Известия Юго-Западного государственного университета. 2020. Т. 23. № 6. С. 176.
Лушников Б.В., Скрыльников Н.Е. Имитационная модель процесса вертикализации экзоскелета нижних конечностей в среде Simmechanics / MATLAB с учетом сухого трения в кинематических парах // Вибрационные технологии, мехатроника и управляемые машины. 2016. С. 261.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин