1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 2, 2021

Проблемы машиностроения и надежности машин, 2021, № 2, стр. 9-16

Автопараметрические колебания при запаздываниях в силах упругости и трения

А. А. Алифов *

Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

* E-mail: alishir@mail.ru

Поступила в редакцию 21.05.2020
После доработки 16.11.2020
Принята к публикации 18.12.2020

Полный текст (PDF)

Аннотация

Рассмотрены смешанные параметрические колебания и автоколебания в системе с неидеальным источником энергии при запаздываниях в силах упругости и трения. Для решения нелинейных уравнений использован метод прямой линеаризации. Выведены условия устойчивости стационарных колебаний. Проведены расчеты и оказалось, что запаздывание приводит к некоторым интересным эффектам. Из-за запаздывания кривые могут вести себя так, как при наличии нелинейной силы упругости, а также при определенных значениях запаздывания верхняя (устойчивая при отсутствии запаздывания) и нижняя ветви амплитудных кривых могут оказаться неустойчивыми.

Ключевые слова: смешанные колебания, параметрические колебания, автоколебания, источник энергии, запаздывание, метод, прямая линеаризация

Во многих современных технических устройствах и технологических процессах при определенных условиях могут возникать различные виды смешанных колебаний (“смесь” или взаимодействие двух и более типов колебаний). Функционирование этих систем поддерживается источниками энергии, имеющими ограниченную мощность. Вопросы энергии и ее потребления связаны не только с поддержанием работы различных технических систем. Они имеют прямое отношение к проблемам экологии, которые остро стоят в настоящее время перед человечеством. Уменьшение потребления энергии даже на несколько процентов может внести немалый вклад в экологическую обстановку на планете. В этом контексте выходит на переднюю позицию с большей значимостью, чем ранее, фундаментальная теория колебательных систем с источниками энергии ограниченной мощности, созданная В.О. Кононенко [1, 2]. Он систематически изучил и обосновал эффект Зоммерфельда, обнаруженный в ходе экспериментов в 1902 г. В связи с экологическими проблемами приведем из [3] следующее: “Деятельность цивилизации привела к тому, что Земля (геосфера, атмосфера, аквасфера, биосфера) пропитана огромным количеством отходов (промышленными, бытовыми, химическими). Однако нельзя забывать, что любым многоэлементным образованиям материи, в том числе экологии Земли, свойственен предел, при достижении которого наступают необратимые изменения [4]. Проблемы экологии (атмосферные, парниковый эффект, разрушение озонового слоя, водные, биологические, глобальное потепление) затрагивают всю природу на Земле и приняли глобальные масштабы. Это со временем может привести к катастрофическим последствиям, как для человека, так и для всего остального живого мира…”. Грамотное использование теории колебательных систем с источниками энергии ограниченной мощности и разработка на ее основе математических моделей различных систем, позволяет рассчитать и подобрать на стадии проектирования машин, механизмов и т.д. источник энергии так, чтобы обеспечить их работу минимальным потреблением энергоресурсов и уровнем нежелательных колебательных процессов [3].

В устройствах различного рода широко распространены запаздывание, которое [5] в механических системах обуславливается внутренним трением в материалах, несовершенством их упругих свойств и др. Как отмечено в работе [6], “звенья с чистым запаздыванием часто встречаются в различных технологических процессах, когда материал перемещается из одной точки в другую с помощью ленточных транспортеров; в системах регулирования толщины листа при прокатке; в системах магнитной записи и воспроизведения и т. д.”. Под действием запаздывания возникают различные колебательные процессы (полезные/вредные). Имеется достаточно большое число работ [7‒12], посвященных изучению колебаний в различных системах с запаздыванием. Однако чаще взаимодействие колебательной системы и источника энергии не учитывается.

Одной из основных проблем нелинейной динамики систем является большая затрата труда для анализа осцилляторных сетей, играющая важную роль в физике, электронике, нейронных сетях, химии и др. [13–16]. Аналитическое исследование нелинейных колебательных систем проводится с помощью трудоемких приближенных методов нелинейной механики [7, 17–21]. От них существенно отличаются методы прямой линеаризации, обладающие на несколько порядков меньшей трудоемкостью и достаточно простые для применения [22–25]. Эти особенности метода весьма существенны при расчете технических устройств на стадии их проектирования. С применением методов прямой линеаризации рассмотрим автоколебательную систему с неидеальным источником энергии, параметрическим возбуждением, запаздыванием в силах упругости и трения. Целью статьи является изучение на основе методов прямой линеаризации совместного влияния различных запаздываний на динамику автопараметрических колебаний при неидеальном источнике энергии.

1. В основу положим широко используемую динамическую модель автоколебательной системы [1, 2, 21, 26–28]. Нелинейные дифференциальные уравнения движения системы с учетом параметрического возбуждения представим в виде

(1)
$\begin{gathered} {\kern 1pt} m\ddot {x} + {{k}_{{{\kern 1pt} 0}}}\dot {x} + {{c}_{0}}x = T(U) - bx\cos \nu t, \\ I\ddot {\varphi } = M(\dot {\varphi }) - {{r}_{0}}T(U), \\ \end{gathered} $
где ${{k}_{0}} = {\text{const}}$ – коэффициент демпфирования; ${{c}_{0}} = {\text{const}}$; $bx\cos \nu t$ – параметрическое возбуждение; $b = {\text{const}}$; $T(U)$ – вызывающая автоколебания нелинейная сила трения; $U = {{r}_{0}}\dot {\varphi }--\dot {x}$; ${{r}_{0}} = {\text{const}}$ – радиус точки приложения силы трения $T(U)$; $\dot {\varphi }$ – скорость вращения двигателя; I – суммарный момент инерции вращающихся частей; $M(\dot {\varphi })$ – разность вращающего момента источника энергии и момента сил сопротивления вращению.

Характеристика силы трения на практике широко распространена в форме

(2)
$T(U) = R(\operatorname{sgn} U - {{\alpha }_{1}}U + {{\alpha }_{3}}{{U}^{3}}),$
где R – нормальная сила реакции; ${{\alpha }_{1}}$ и ${{\alpha }_{3}}$ – положительные постоянные; $\operatorname{sgn} U = 1$ при $U > 0$ и $\operatorname{sgn} U = - 1$ при $U < 0$.

Характеристика (2) наблюдалась также в условиях космического эксперимента [29]. Для большей общности представим характеристику трения в форме

$T(U) = R\left[ {\operatorname{sgn} U + f(\dot {x})} \right],\quad f(\dot {x}) = \sum\limits_i {{{\alpha }_{i}}{{U}^{i}}} = \sum\limits_{n = 0}^5 {{{\delta }_{n}}{{{\dot {x}}}^{n}}} ,$
${{\delta }_{0}} = {{\alpha }_{1}}V + {{\alpha }_{2}}{{V}^{2}} + {{\alpha }_{3}}{{V}^{3}} + {{\alpha }_{4}}{{V}^{4}} + {{\alpha }_{5}}{{V}^{5}},$
${{\delta }_{1}} = - ({{\alpha }_{1}} + 2{{\alpha }_{2}}V + 3{{\alpha }_{3}}{{V}^{2}} + 4{{\alpha }_{4}}{{V}^{3}} + 5{{\alpha }_{5}}{{V}^{4}}),$
${{\delta }_{2}} = {{\alpha }_{2}} + 3{{\alpha }_{3}}V + 6{{\alpha }_{4}}{{V}^{2}} + 10{{\alpha }_{5}}{{V}^{3}},\quad {{\delta }_{3}} = - ({{\alpha }_{3}} + 4{{\alpha }_{4}}V + 10{{\alpha }_{5}}{{V}^{2}}),$
${{\delta }_{4}} = {{\alpha }_{4}} + 5{{\alpha }_{5}}V,\quad {{\delta }_{5}} = - {{\alpha }_{5}}.$

Нелинейную функцию $f(\dot {x})$, используя метод прямой линеаризации [22, 23], можно заменить линейной функцией

(3)
${{f}_{*}}(\dot {x}) = {{B}_{f}} + {{k}_{f}}\dot {x},$
где ${{B}_{f}}$, ${{k}_{f}}$ являются коэффициентами линеаризации, которые определяются выражениями

${{B}_{f}} = \sum\limits_n {{{N}_{n}}{{\alpha }_{n}}{{{v}}^{n}}} ,\quad n = 0,2,4\quad (n - {\text{четное}}),$
${{k}_{f}} = \sum\limits_n {{{\alpha }_{n}}{{{\bar {N}}}_{n}}{{{v}}^{{n - 1}}}} ,\quad n = 1,3,5\quad (n - {\text{нечетное}}),$
${{N}_{n}}{\kern 1pt} = {{(2r + 1)} \mathord{\left/ {\vphantom {{(2r + 1)} {(2r + 1 + n)}}} \right. \kern-0em} {(2r + 1 + n)}},\quad {{\bar {N}}_{n}} = {{(2r + 3)} \mathord{\left/ {\vphantom {{(2r + 3)} {(2r + 2 + n)}}} \right. \kern-0em} {(2r + 2 + n)}},\quad \upsilon = \max \left| {\dot {x}} \right|.$

Отметим, что в выражениях ${{N}_{n}}$ и ${{\bar {N}}_{n}}$ символ r является параметром точности линеаризации. Независимо от его величины имеют место ${{N}_{n}} = 1$ для n = 0 и ${{\bar {N}}_{n}} = 1$ для n = 1. Интервал выбора этого параметра не ограничен [22, 23], но достаточен выбор в пределах (0–2).

Представим силу трения $T(U)$ зависящей от запаздывания Δ, т.е. в форме $T({{U}_{\Delta }})$, в которой ${{U}_{\Delta }} = {{r}_{0}}\dot {\varphi } - {{\dot {x}}_{\Delta }}$, ${{\dot {x}}_{\Delta }} = \dot {x}(t - \Delta )$. Примем, что сила упругости также зависит от запаздывания, учитываемого посредством слагаемого ${{c}_{1}}{{x}_{{\tau }}}$, ${{x}_{{\tau }}} = x(t - \tau )$, τ – временной фактор запаздывания, ${{c}_{1}} = {\text{const}}$. Тогда уравнения (1) в связи с (3) примут вид

(4)
$\begin{gathered} m{\kern 1pt} \ddot {x} + {{k}_{0}}\dot {x} + {{c}_{0}}x = R(\operatorname{sgn} {{U}_{\Delta }} + {{B}_{f}} + {{k}_{f}}{{{\dot {x}}}_{\Delta }}) - {{c}_{1}}{{x}_{\tau }} - bx\cos \nu t, \\ I\ddot {\varphi } = M(\dot {\varphi }) - {{r}_{0}}R(\operatorname{sgn} {{U}_{\Delta }} + {{B}_{f}} + {{k}_{f}}{{{\dot {x}}}_{\Delta }}). \\ \end{gathered} $

2. Решение (4) можно выполнить с помощью метода замены переменных с усреднением [22] и описанной в [25] процедуры для колебательных систем с ограниченным возбуждением. Метод позволяет рассмотреть нестационарные и стационарные процессы. В этом методе для нелинейного уравнения с линеаризованными нелинейными функциями на основе формы решения

(5)
$x = a\cos \psi {\text{,}}\quad \dot {x} = - \upsilon \sin \psi {\text{,}}\quad \psi = pt + \xi ,$
выведены стандартной формы уравнения для определения нестационарных значений $\upsilon $ и ξ.

Используя эту стандартную форму и процедуру с учетом $\upsilon = a{\kern 1pt} p$, $p = {\nu \mathord{\left/ {\vphantom {\nu 2}} \right. \kern-0em} 2},$ ${{x}_{\tau }}$ = = $a\cos (\psi - p\tau )$, ${{\dot {x}}_{\Delta }} = - \upsilon \sin {\kern 1pt} (\psi - p\Delta )$, получим из (4) следующие уравнения для нестационарных значений амплитуды а, фазы ξ и скорости u:

а) $u \geqslant ap$

$\frac{{da}}{{dt}} = - \frac{{a({{k}_{0}} - {{T}_{0}}{{k}_{f}}\cos p\Delta {\kern 1pt} )}}{{2m}} + \frac{{{{c}_{1}}a}}{{2pm}}\sin p{\tau } + \frac{{ba}}{{4pm}}\sin 2{\xi ,}$
(6a)
$\frac{{d{\xi }}}{{dt}} = \frac{{{\omega }_{0}^{2} - {{p}^{2}}}}{{2p}} + \frac{{{{c}_{1}}}}{{2pm}}\cos p{\tau } - \frac{{{{T}_{0}}{{k}_{f}}}}{{2m}}sinp\Delta + \frac{b}{{4pm{\kern 1pt} }}\cos 2{\xi ,}$
$\frac{{du}}{{dt}} = \frac{{{{r}_{0}}}}{I}\left[ {M\left( {\frac{u}{r}} \right) - {{r}_{0}}{\kern 1pt} {{T}_{0}}{\kern 1pt} (1 + {{B}_{f}})} \right];$

б) $u < ap$

$\frac{{da}}{{dt}} = - \frac{a}{{2m}}\left[ {({{k}_{0}} - {{T}_{0}}{{k}_{f}}\cos p\Delta {\kern 1pt} ) + \frac{{4{{T}_{0}}}}{{\pi {{a}^{2}}{{p}^{2}}}}\sqrt {{{a}^{2}}{{p}^{2}} - {{u}^{2}}} } \right] + \frac{{{{c}_{1}}a}}{{2pm{\kern 1pt} }}\sin p\tau + \frac{{ba}}{{4pm{\kern 1pt} }}\sin 2\xi {\text{,}}$
(6б)
$\frac{{d\xi }}{{dt}} = \frac{{\omega _{0}^{2} - {{p}^{2}}}}{{2p}} + \frac{{{{c}_{1}}}}{{2pm}}\cos p\tau - \frac{{{{T}_{0}}{\kern 1pt} {{k}_{f}}}}{{2m}}sinp\Delta + \frac{b}{{4pm}}\cos 2\xi {\text{,}}$
$\frac{{du}}{{dt}} = \frac{{{{r}_{0}}}}{I}\left[ {M\left( {\frac{u}{r}} \right) - {{r}_{0}}{\kern 1pt} {{T}_{0}}{\kern 1pt} (1 + {{B}_{f}}) - \frac{{{{r}_{0}}{{T}_{0}}}}{\pi }(3{\pi } - 2{{\psi }_{*}})} \right].$

Здесь $u = {{r}_{0}}\Omega $, ${{\psi }_{*}} = 2\pi - \arcsin ({u \mathord{\left/ {\vphantom {u {ap)}}} \right. \kern-0em} {ap)}}$, $\omega _{0}^{2} = {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} m}} \right. \kern-0em} m}$. Отметим, что при выводе (6б) использован прием, описанный в [26].

Из (6а) при $\dot {a} = 0$, $\dot {\xi } = 0$, $\dot {u} = 0$ следуют уравнения для стационарных движений в случае $u \geqslant ap$, откуда имеем соотношения для определения амплитуды и фазы

(7)
${{A}^{2}} + {{E}^{2}} = 0.25{\kern 1pt} {{b}^{2}},\quad \operatorname{tg} 2\xi = - {A \mathord{\left/ {\vphantom {A E}} \right. \kern-0em} E},$
где $A = p({{k}_{0}} - {{T}_{0}}{{k}_{f}}\cos p\Delta ) - {{c}_{1}}\sin p\tau $, $E = m({\omega }_{0}^{2} - {{p}^{2}}) - p{{T}_{0}}{{k}_{f}}sinp\Delta + {{c}_{1}}\cos p{\tau }$.

В случае $u < ap$ для амплитуды имеем приближенную формулу ap ≈ u. Заметим, что в выражениях α0, …, α5, которые входят в ${{k}_{f}}$, в результате усреднения осуществляется замена $V = {{r}_{0}}\dot {\varphi }$ на $u = {{r}_{0}}\Omega $.

Из условия $\dot {u} = 0$ получим уравнение для определения стационарных значений скорости

(8)
$M({u \mathord{\left/ {\vphantom {u {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}) - S(u) = 0,$
где

${\text{a}})\quad u \geqslant ap\quad S(u) = {{r}_{0}}R{\kern 1pt} (1 + {{B}_{F}}),$
${\text{б}})\quad u < ap\quad S(u) = {{r}_{0}}R\,[(1 - {{B}_{F}}) + {{\pi }^{{ - 1}}}(3\pi - 2{{\psi }_{*}})].$

С учетом приближенного равенства ap ≈ u для амплитуды выражение нагрузки S(u) на источник энергии упрощается в случае $u < ap$. Стационарные значения скорости u можно определить точкой пересечения графиков $M({u \mathord{\left/ {\vphantom {u {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}})$ и S(u).

3. Для вывода условий устойчивости стационарного движения составляем уравнения в вариациях для (6) и пользуемся критериями Рауса–Гурвица. В результате имеем условия устойчивости

(9)
${{D}_{1}} > 0,\quad {{D}_{3}} > 0,\quad {{D}_{1}}{{D}_{2}} - {{D}_{3}} > 0,$
где D1 = $ - ({{b}_{{11}}} + {{b}_{{22}}} + {{b}_{{33}}})$, ${{D}_{2}} = {{b}_{{11}}}{{b}_{{33}}} + {{b}_{{11}}}{{b}_{{22}}} + {{b}_{{22}}}{{b}_{{33}}} - {{b}_{{23}}}{{b}_{{32}}} - {{b}_{{12}}}{{b}_{{21}}}$ – b13b31, D3 = = ${{b}_{{11}}}{{b}_{{23}}}{{b}_{{32}}}$ + ${{b}_{{12}}}{{b}_{{21}}}{{b}_{{33}}}$ – ${{b}_{{11}}}{{b}_{{22}}}{{b}_{{33}}} - {{b}_{{12}}}{{b}_{{23}}}{{b}_{{31}}} - {{b}_{{13}}}{{b}_{{21}}}{{b}_{{32}}}$.

Для случая $u \geqslant ap$ имеем

${{b}_{{11}}} = \frac{{{{r}_{0}}}}{J}\left( {Q - {{r}_{0}}R\frac{{\partial {{B}_{f}}}}{{\partial u}}} \right),\quad {{b}_{{12}}} = - \frac{{r_{0}^{2}R}}{J}\frac{{\partial {{B}_{f}}}}{{\partial a}},\quad {{b}_{{13}}} = 0,$
${{b}_{{21}}} = \frac{{aR{\kern 1pt} }}{{2m}}\frac{{\partial {{k}_{f}}}}{{\partial u}}\cos p\Delta ,\quad {{b}_{{22}}} = - \frac{1}{{2m}}\left( {{{k}_{0}} - R{{k}_{f}}\cos p\Delta - aR{\kern 1pt} \frac{{\partial {{k}_{f}}}}{{\partial a}}\cos p\Delta } \right),$
${{b}_{{23}}} = 0,\quad {{b}_{{31}}} = \frac{R}{{2m}}\frac{{\partial {{k}_{f}}}}{{\partial u}}sinp\Delta ,\quad {{b}_{{32}}} = \frac{{R{\kern 1pt} }}{{2m}}\frac{{\partial {{k}_{f}}}}{{\partial a}}sinp\Delta ,\quad {{b}_{{33}}} = 0,$
где $Q = \frac{d}{{du}}M\left( {\frac{u}{r}} \right)$.

В случае скоростей $u < ap$ коэффициенты ${{b}_{{13}}}$, ${{b}_{{23}}}$, ${{b}_{{31}}}$, ${{b}_{{33}}}$ остаются такими же, изменяются (с добавлением одного слагаемого, содержащего $\sqrt {{{a}^{2}}{{p}^{2}} - {{u}^{2}}} $) следующие:

${{b}_{{11}}} = \frac{{{{r}_{0}}}}{J}\left[ {Q - {{r}_{0}}R\frac{{\partial {{B}_{f}}}}{{\partial u}} - \frac{{2{{r}_{0}}R}}{{{\pi }\sqrt {{{a}^{2}}{{p}^{2}} - {{u}^{2}}} }}} \right],\quad {{b}_{{12}}} = - \frac{{r_{0}^{2}R}}{J}\left[ {\frac{{\partial {{B}_{f}}}}{{\partial a}} + \frac{{2u}}{{{\pi }a\sqrt {{{a}^{2}}{{p}^{2}} - {{u}^{2}}} }}} \right],$
${{b}_{{21}}} = \frac{a}{{2m}}\left[ {R\frac{{\partial {{k}_{f}}}}{{\partial u}}\cos p\Delta + \frac{{4uR}}{{{\pi }{{a}^{2}}{{p}^{2}}\sqrt {{{a}^{2}}{{p}^{2}} - {{u}^{2}}} }}} \right],$
${{b}_{{22}}} = - \frac{1}{{2m}}\left[ {{{k}_{0}} - R{{k}_{f}}\cos p\Delta - aR\frac{{\partial {{k}_{f}}}}{{\partial a}}\cos p\Delta + \frac{{4R{{u}^{2}}}}{{{\pi }{{a}^{2}}{{p}^{2}}\sqrt {{{a}^{2}}{{p}^{2}} - {{u}^{2}}} }}} \right].$

С учетом $\dot {\varphi } = \Omega $, $u = r\Omega $ при усреднении, имеем

$\frac{{\partial {{B}_{f}}}}{{\partial u}} = \frac{{\partial {{\delta }_{0}}}}{{\partial u}} + {{N}_{2}}{{(ap)}^{2}}\frac{{\partial {{\delta }_{2}}}}{{\partial u}} + {{N}_{4}}{{(ap)}^{4}}\frac{{\partial {{\delta }_{4}}}}{{\partial u}},$
$\frac{{\partial {{k}_{f}}}}{{\partial u}} = {{\bar {N}}_{1}}\frac{{\partial {{\delta }_{1}}}}{{\partial u}} + {{\bar {N}}_{3}}{{(ap)}^{2}}\frac{{\partial {{\delta }_{3}}}}{{\partial u}} + {{\bar {N}}_{5}}{{(ap)}^{4}}\frac{{\partial {{\delta }_{5}}}}{{\partial u}},$
$\frac{{\partial {{B}_{f}}}}{{\partial a}} = 2a{{p}^{2}}({{N}_{2}}{{\delta }_{2}} + 2{{N}_{4}}{{\delta }_{4}}{{a}^{2}}{{p}^{2}}),\quad \frac{{\partial {{k}_{f}}}}{{\partial a}} = 2a{{p}^{2}}({{\bar {N}}_{3}}{{\delta }_{3}} + 2{{\bar {N}}_{5}}{\kern 1pt} {{\delta }_{5}}{{a}^{2}}{{p}^{2}}),$
${{\delta }_{0}} = {{\alpha }_{1}}u + {{\alpha }_{2}}{{u}^{2}} + {{\alpha }_{3}}{{u}^{3}} + {{\alpha }_{4}}{{u}^{4}} + {{\alpha }_{5}}{{u}^{5}},\quad {{\delta }_{1}} = - ({{\alpha }_{1}} + 2{{\alpha }_{2}}u + 3{{\alpha }_{3}}{{u}^{2}} + 4{{\alpha }_{4}}{{u}^{3}} + 5{{\alpha }_{5}}{{u}^{4}}),$
${{\delta }_{2}} = {{\alpha }_{2}} + 3{{\alpha }_{3}}u + 6{{\alpha }_{4}}{{u}^{2}} + 10{{\alpha }_{5}}{{u}^{3}},\quad {{\delta }_{3}} = - ({{\alpha }_{3}} + 4{{\alpha }_{4}}u + 10{{\alpha }_{5}}{{u}^{2}}),$
${{\delta }_{4}} = {{\alpha }_{4}} + 5{{\alpha }_{5}}u,\quad {{\delta }_{5}} = - {{\alpha }_{5}},$
$\frac{{\partial {{\delta }_{0}}}}{{\partial u}} = {{\alpha }_{1}} + 2{{\alpha }_{2}}u + 3{{\alpha }_{3}}{{u}^{2}} + 4{{\alpha }_{4}}{{u}^{3}} + 5{{\alpha }_{5}}{{u}^{4}},\quad \frac{{\partial {{\delta }_{1}}}}{{\partial u}} = - 2({{\alpha }_{2}} + 3{{\alpha }_{3}}u + 6{{\alpha }_{4}}{{u}^{2}} + 10{{\alpha }_{5}}{{u}^{3}}),$
$\frac{{\partial {{\delta }_{2}}}}{{\partial u}} = 3({{\alpha }_{3}} + 4{{\alpha }_{4}}u + 10{{\alpha }_{5}}{{u}^{2}}),\quad \frac{{\partial {{\delta }_{3}}}}{{\partial u}} = - 4({{\alpha }_{4}} + 5{{\alpha }_{5}}u),\quad \frac{{\partial {{\delta }_{4}}}}{{\partial u}} = 5{{\alpha }_{5}},\quad \frac{{\partial {{\delta }_{5}}}}{{\partial u}} = 0.$

Учитываются лишь четные степени n и соответственно ${{\delta }_{0}}$, ${{\delta }_{2}}$, ${{\delta }_{4}}$ при вычислении ${{\partial {{B}_{f}}} \mathord{\left/ {\vphantom {{\partial {{B}_{f}}} {\partial u}}} \right. \kern-0em} {\partial u}}$, ${{\partial {{B}_{f}}} \mathord{\left/ {\vphantom {{\partial {{B}_{f}}} {\partial a}}} \right. \kern-0em} {\partial a}}$. А при вычислении ${{\partial {{k}_{f}}} \mathord{\left/ {\vphantom {{\partial {{k}_{f}}} {\partial u}}} \right. \kern-0em} {\partial u}}$, ${{\partial {{k}_{f}}} \mathord{\left/ {\vphantom {{\partial {{k}_{f}}} {\partial a}}} \right. \kern-0em} {\partial a}}$ используются нечетные степени n и соответственно ${{\delta }_{1}}$, ${{\delta }_{3}}$, ${{\delta }_{5}}$.

4. Были проведены расчеты для получения информации о влиянии запаздывания на динамику системы, а также сравнительной оценки результатов по методу прямой линеаризации и асимптотического метода усреднения нелинейной механики. При расчетах использованы характеристика трения в форме (2) и параметры: ${{\omega }_{0}} = 1$ c–1; $m = 1$ кгс с см–1; $b = 0.07$ кгс см–1; ${{c}_{1}} = 0.05$ кгс см–1; $k = 0.02$ кгс с см–1; $R = 0.5$ кгс; ${{\alpha }_{1}} = 0.84{\kern 1pt} $ с см–1; ${{\alpha }_{3}} = 0.18{\kern 1pt} $ с3 см–3, ${{r}_{0}} = 1$ см, $I = 1$ кгс с см2. Для запаздываний использованы величины pΔ и pτ из интервала (0, 3π/2).

Зависимости амплитуды от частоты a(p) получены при u = 1.2 (рис. 1–3). На всех кривых колебания с амплитудами устойчивы в пределах заштрихованных секторов для крутизны $Q = \frac{d}{{du}}M({u \mathord{\left/ {\vphantom {u {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}})$ характеристики источника энергии. Все кривые получены при параметре точности линеаризации r = 1.5 (${{\bar {N}}_{n}}$ для ${{k}_{f}}$) и полностью совпадают с результатами на основе асимптотического метода усреднения.

Рис. 1.

Амплитудно-частотные кривые при Δ = π/2: кривая 1 – τ = 0; кривая 2 – τ = π/2; кривая 3 – τ = π.

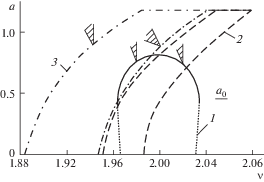
Рис. 2.

Амплитудно-частотные кривые при Δ = π: кривая 1 – τ = 0; кривая 2 – τ = π/2; кривая 3 – τ = π.

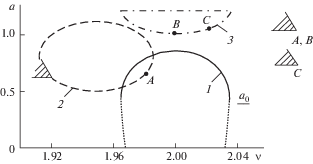
Рис. 3.

Амплитудно-частотные кривые при Δ = 3π/2: кривая 1 – τ = 0; кривая 2 – τ = π/2; кривая 3 – τ = π.

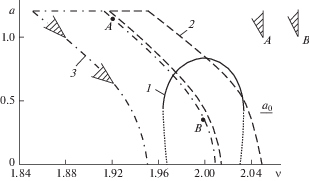
Кривые 1 на всех рисунках соответствуют отсутствию запаздывания (${{с}_{1}} = 0$, Δ = 0, τ = 0), приведены для сравнения и ${{a}_{0}}$ указывает амплитуду автоколебаний. Сплошная часть кривой 1 отражает устойчивые колебания, пунктирная – неустойчивые при идеальном источнике энергии. В случае неидеального источника энергии реализуемость сплошной части кривой 1 зависит от крутизны характеристики источника, а пунктирная часть 1 неустойчива в любом случае.

Влияние запаздываний приводит к интересным эффектам. При Δ = π/2, Δ = 3π/2 как верхняя (устойчивая при отсутствии запаздывания в соответствии с кривой 1), так и нижняя ветви кривых 2 оказываются неустойчивыми. Однако при Δ = π наблюдается особенность: верхняя ветвь оказывается неустойчивой при любой крутизне характеристики источника энергии, вплоть до идеального, а нижняя ветвь – устойчивой в зависимости от крутизны. Верхние и нижние ветви кривых 3 также могут оказаться устойчивыми, что тоже зависит от крутизны характеристики источника энергии. Кривые 2 и 3 при Δ = π/2 и Δ = 3π/2 ведут себя несколько аналогично тому, что получается при нелинейной силе упругости. Для пояснения примем, что упругая сила представлена в первом уравнении (1) характеристикой $f(x) = {{c}_{0}}x + {\gamma }{{x}^{3}}$. В случае $\gamma > 0$ имеет место жесткая характеристика, а при $\gamma < 0$ – мягкая. Как известно, при отсутствии запаздываний и $\gamma > 0$ амплитудные кривые наклоняются вправо, а при $\gamma < 0$ – влево [26]. Аналогичное поведение кривых 2 и 3 видно при Δ = π/2 и Δ = 3π/2, они наклонены вправо при Δ = π/2 и влево – при Δ = 3π/2. Такой эффект обусловлен влиянием запаздывания по трению. При наличии запаздывания по упругости и его отсутствии по трению нет такого эффекта. Запаздывание по упругости лишь сдвигает резонансную зону вправо или влево относительно случая его отсутствия.

5. Наличие запаздываний приводит к некоторым эффектам. При определенных значениях запаздывания по трению амплитудно-частотные кривые наклоняются вправо и влево соответственно как при жесткой и мягкой характеристиках нелинейной силы упругости. В связи с такой аналогией кривых, обусловленных нелинейной упругостью и запаздыванием в трении, возникает вопрос: как по форме кривых в реальных устройствах определить источник колебаний (нелинейная упругость или запаздывание в трении). Чтобы ответить на него необходимо многостороннее изучение устройства.

Список литературы

  1. Кононенко В.О. Колебательные системы с ограниченным возбуждением. М.: Наука, 1964. 236 с.

  2. Kononenko V.O. Vibrating Systems with Limited Power-Supply. London: Iliffe. 1969.

  3. Alifov A.A. About calculation of self-oscillatory system delayed and limited excitation // “Ölçmə və keyfiyyət: problemlər, perspektivlər” mövzusunda Beynəlxalq Elmi-texniki konfransın materialları, 21–23 noyabr 2018: AzTU. Bakı. Azərbaycan. 2018. P. 289.

  4. Алифов А.А. Фундаментальный принцип, управляющий Вселенной. М. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2012. 408 с.

  5. Энциклопедия по машиностроению. https://mash-xxl.info/info/174754/

  6. Теория автоматического управления. Теория линейных систем автоматического управления / Под ред. А.А. Воронова. 2-е изд., перераб. и доп. М.: Высш. шк., 1986. Ч. I. 367 с.

  7. Рубаник В.П. Колебания квазилинейных систем с запаздыванием. М.: Наука, 1969. 288 с.

  8. Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.А. Введение в теорию нелинейных колебаний. М.: Наука, 1976. 256 с.

  9. Жирнов Б.М. Об автоколебаниях механической системы с двумя степенями свободы при наличии запаздывания // Прикладная механика. 1973. Т. 9. № 10. С. 83.

  10. Жирнов Б.М. Одночастотные резонансные колебания фрикционной автоколебательной системы с запаздыванием при внешнем возмущении // Прикладная механика. 1978. Т. 14. № 9. С. 102.

  11. Асташев В.К., Герц М.Е. Автоколебания вязко-упругого стержня с ограничителями при действии запаздывающей силы // Машиноведение. 1973. № 5. С. 3.

  12. Абдиев Ф.К. Автоколебания системы с запаздыванием и с неидеальным источником энергии // Изв. АН АзССР. Серия физико-технических и математических наук. 1983. № 4. С. 134.

  13. Gourary M.M., Rusakov S.G. Analysis of Oscillator Ensemble with Dynamic Couplings // AIMEE 2018. The Second International Conference of Artificial Intelligence, Medical Engineering, Education. 2018. P. 150.

  14. Acebrón J.A. et al. The Kuramoto model: A simple paradigm for synchronization phenomena // Reviews of Modern Physics. 2005. V. 77. № 1. P. 137.

  15. Bhansali P., Roychowdhury J. Injection Locking Analysis and Simulation of Weak-ly Coupled Oscillator Networks // In: Li P. (eds.) Simulation and Verification of Electronic and Biological Systems. Springer Science+Business Media B.V. 2011. P. 71.

  16. Ashwin P., Coombes S., Nicks R.J. Mathematical Frameworks for Oscillatory Network Dynamics in Neuroscience // Journal of Mathematical Neuroscience. 2016. V. 6. № 2. P. 1.

  17. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 504 с.

  18. Tondl A. On the interaction between self-exited and parametric vibrations // National Research Institute for Machine Design Bechovice. Series: Monographs and Memoranda, 1978. № 25. 127 p.

  19. Хаяси Т. Нелинейные колебания в физических системах. М.: Мир, 1968. 432 с.

  20. Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1981. 400 с.

  21. Вибрации в технике: Справочник. В 6-ти т. / Ред. совет: В.Н. Челомей (пред.). Т. 5. Колебания нелинейных механических систем / Под ред. И.И. Блехмана. М.: Машиностроение, 1979. 351 с.

  22. Алифов А.А. Методы прямой линеаризации для расчета нелинейных систем. М. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2015. 74 с.

  23. Alifov A.A. Method of the Direct Linearization of Mixed Nonlinearities // Journal of Machinery Manufacture and Reliability. 2017. V. 46. № 2. P. 128.

  24. Alifov A.A., Farzaliev M.G., Jafarov E.N. Dynamics of a Self-Oscillatory System with an Energy Source // Russian Engineering Research. 2018. V. 38. № 4. P. 260.

  25. Alifov A.A. Calculating Mixed Forced and Self-Oscillations for Delayed Elastic Constraint and a Limited Power Energy Source // Journal of Machinery Manufacture and Reliability. 2020. V. 49. № 2. P. 105. https://doi.org/10.3103/S1052618820020053

  26. Alifov A.A., Frolov K.V. Interaction of Nonlinear Oscillatory Systems with Energy Sources. New York: Hemisphere Pub. Corp. Taylor & Francis Group. 1990. P. 327.

  27. Журавлёв В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 328 с.

  28. Климов Д.М. Об одном виде автоколебаний в системе с сухим трением // Изв. РАН. МТТ. 2003. № 3. С. 6.

  29. Броновец М.А., Журавлёв В.Ф. Об автоколебаниях в системах измерения сил трения // Изв. РАН. МТТ. 2012. № 3. С. 3.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал