Проблемы машиностроения и надежности машин, 2021, № 3, стр. 47-54

Физико-математическое моделирование поверхности для нанесения износостойких покрытий плазменным напылением

С. В. Карцев^*

Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

Поступила в редакцию 03.08.2020
После доработки 21.01.2021
Принята к публикации 24.02.2021

DOI: 10.31857/S0235711921030068

Аннотация

В статье с помощью теории подобия и размерности исследуется поверхность детали тел вращения перед плазменным напылением износостойких покрытий, что играет важную роль в активизации процессов образования связи между напыляемыми частицами и поверхностью детали. Рассмотрены физические процессы взаимодействия поверхности детали перед плазменным напылением износостойких покрытий с термоабразивной струей. Для физико-математического моделирования использованы параметры: средний диаметр частиц, средняя плотность материала детали, плотность материала частицы, пройденный частицей путь, начальная скорость частицы, ускорение движения частицы, ударная вязкость металла, для отражения процесса движения частицы абразива в термоабразивной струе. Получено уравнение регрессии и определены максимальная энергия абразивной частицы, которая будет подводиться при угле наклона относительно детали и соответствующая этим параметрам сумма скоростей частиц в зависимости от угла наклона в момент соударения.

Ключевые слова: термоабразивная струя, абразивная частица, плазменное напыление, износостойкие покрытия, физико-математическое моделирование

Подготовка поверхности деталей перед плазменным напылением износостойких покрытий играет важную роль в активизации процессов образования связи между напыляемыми частицами и основой. Простейшим и наиболее распространенным способом является струйно-абразивная обработка, заключающаяся в воздействии на обрабатываемую поверхность струи твердых частиц, движущихся с большой скоростью. Недостатком технического решения данного способа является то, что не обеспечивается необходимая шероховатость и активизация процессов на поверхности в связи с использованием при обработке абразивных сыпучих материалов содержащих легко разрушаемые минералы. Нестабильность свойств обработанной поверхности является следствием несоблюдения необходимых режимов обработки, что часто приводит к разным результатам прочности сцепления покрытия с основой [2, 10]. Для физико-математического моделирования рассматривается задача: за счет воздействия струи нагретых твердых частиц на обрабатываемую поверхность детали обеспечить заданную шероховатость поверхности и активизацию процессов образования связи между напыляемыми частицами и поверхностью детали. Частицы движутся с высокой скоростью с одновременным нагревом обрабатываемой поверхности детали до температуры, которая обеспечит качественное сцепление напыляемого покрытия с поверхностью, на которую оно наносится, при этом обеспечит оптимальный угол обработки поверхности термоабразивной струей. Основными факторами, определяющими свойства обработанной поверхности детали, являются вид, размер, форма применяемых частиц, их расход на единицу обрабатываемой поверхности, скорость соударения с поверхностью детали и угол наклона термоабразивной струи.

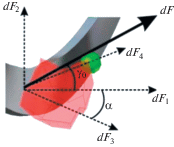
Процессы, происходящие в металле, из которого изготовлена деталь при термоабразивном воздействии, оказывают большое влияние на состояние поверхности. Степень влияния такого воздействия зависит от технологических режимов обработки, характеристик абразивных частиц и физико-механических свойств материала, из которого изготовлена деталь [4, 9]. Рассмотрим физические процессы взаимодействия поверхности детали перед плазменным напылением износостойких покрытий с термоабразивной струей. При термоабразивном внедрении частиц в поверхность детали волны пластического деформирования воздействуют не только на срезаемый слой, но и на структуру металла, расположенного по ходу движения частиц за линией среза [3]. Схема действия сил на поверхность детали представлена на рис. 1. Величины сил, действующих на поверхность, определяются выражением

(1)

$\frac{{dF}}{{dt}} = 2mV\cos \gamma ;\quad dF = {\text{ }}2mV\cos \gamma dt.$

Рис. 1.

Схема действия сил на поверхность детали: γ – угол наклона абразивной частицы; α – угол подъема абразивной частицы.

Из выражения (1) видно, что воздействующие силы зависят от векторной суммы скоростей поверхности детали и абразива V и угла ее наклона γ, а соответственно и подводимая частицей энергия, количество которой и будет устанавливать характер процесса съема металла с поверхности детали [7].

Из рис. 1 видно, что сила, направленная параллельно оси детали есть: dF₁ = dF cos γ (составляющая сила dF). Сила, направленная перпендикулярно оси детали есть: dF₂ = = dF sin γ (радиальная сила, составляющая силы dF). Аксиальная сила: dF₃ = = dF cos α cos γ (составляющая силы dF₁). Если динамическую модель, взаимодействия тел строить относительно какой-либо точки на поверхности детали, то подводимая кинетическая энергия, рассчитывается по формуле

$Т = \frac{{m{{V}^{2}}}}{2} = \frac{{m{{{(\vec {z} + \vec {u})}}^{2}}}}{2},$

где m – масса абразивной частицы, кг; V – вектор скорости абразивной частицы, м/с; $\vec {z}$ – вектор скорости точки на плоскости детали, м/с; $\vec {u}$ – вектор средней скорости абразивной частицы, м/с.

Расчет модуля средней скорости абразивной частицы, учитывая множество сопутствующих динамических процессов взаимодействия даже при упрощенной системе моделирования произвести невозможно. Данная задача решена с помощью теории подобия и размерности, в частности пи-теоремы Бэкингема (англ. the method of dimensions) [5, 6].

Закономерности физического явления воздействия термоабразивной среды на поверхность восстанавливаемой детали описываются уравнением, связывающим между собой величины, существенные для процесса и характерные для механики газа. Течение процесса характеризуется определенным числом физических параметров (X₁, X₂, X₃, …, X_i), размерности которых можно выразить через k базовых единиц измерения, так что i > k. Все остальные в количестве (i – 1), будучи независимыми переменными, являются аргументами, из которых компонуются определяющие числа подобия [8, 10]. Их количество в силу независимости действия различных факторов должно быть равно числу физических явлений, сопровождающих данный процесс. Среди определяющих параметров в количестве (i – 1) имеются такие, при отсутствии которых не могут произойти сами физические явления. Они составляют главную причину происходящего, и потому эти параметры и их размерности являются первоначальными. Число первоначальных аргументов m₀ должно быть равно общему количеству определяющих параметров (i – 1) за вычетом базовых размерностей, характерных для данного процесса

${{m}_{0}} = i--k--1.$

Тогда общее число безразмерных комплексов, характеризующих процесс, составит

$m = {{m}_{0}} + 1 = i--k.$

В данной системе физико-математического моделирования для отражения процесса движения частицы абразива в термоабразивной струе достаточно семи параметров (i = 7): d – средний диаметр частиц; ρ – средняя плотность материала детали; ${{\rho }_{m}}$ – плотность материала частицы; l – пройденный частицей путь; u₀ – начальная скорость частицы; a – ускорение движения частицы; η – ударная вязкость материала детали. Тогда процесс движения частицы абразива в термоабразивной среде можно записать в виде функции

$f(d,\rho ,{{\rho }_{m}},{{u}_{0}},a,\eta ,l) = 0.$

Вид этой функции не меняется при изменении масштабов единиц в выбранном классе систем единиц [1]. Выпишем размерности величин, входящих в это соотношение

(2)

$\begin{gathered} \left[ d \right] = L;\quad [{{\rho }_{m}}] = M{{L}^{{ - 3}}};\quad \left[ \rho \right] = M{{L}^{{ - 3}}};\quad \left[ l \right] = L;\quad \left[ u \right] = L{{\tau }^{{ - 1}}}; \\ \left[ \eta \right] = M{{L}^{{ - 1}}}{{\tau }^{{ - 1}}};\quad [a] = L{{\tau }^{{ - 2}}}, \\ \end{gathered} $

где M – масса; L – расстояние; τ – время.

Из этого следует, что минимальное число первичных размерностей, из которых образованы все остальные, равно трем. Поэтому в данном случае число безразмерных параметров, характеризующих движение частицы в термоабразивной струе, составит

$m = (7--3) = 4.$

В соответствии с размерностью величин (2) запишем произведение степеней параметров, наложив на него условие нулевой размерности

$\Pi = u_{{}}^{{{{n}_{1}}}}{{d}^{{{{n}_{2}}}}}{{(\rho _{т}^{{}} - \rho )}^{{{{n}_{3}}}}}{{а}^{{{{n}_{4}}}}}\rho _{{}}^{{{{n}_{5}}}}{{\eta }^{{{{n}_{6}}}}}{{l}^{{{{n}_{7}}}}}) = {{M}^{0}}{{L}^{0}}{{\tau }^{0}}.$

Подставляя вместо параметров размерность величин, получим выражение

$\Pi = (L{{\tau }^{{ - 1}}})_{{}}^{{{{n}_{1}}}}{{(L)}^{{{{n}_{2}}}}}{{(M{{L}^{{ - 3}}})}^{{{{n}_{3}}}}}{{(L{{\tau }^{{ - 2}}})}^{{{{n}_{4}}}}}{{(M{{L}^{{ - 3}}})}^{{{{n}_{5}}}}}{{(M{{L}^{{ - 1}}}{{\tau }^{{ - 2}}})}^{{{{n}_{6}}}}}{{(L)}^{{{{n}_{7}}}}} = {{M}^{0}}{{L}^{0}}{{\tau }^{0}},$

и систему уравнений

(3)

$\left. \begin{gathered} {{n}_{1}} + {{n}_{2}} - 3{{n}_{3}} + {{n}_{4}} - 3{{n}_{5}} - {{n}_{6}} + {{n}_{7}} = 0, \\ {{n}_{3}} + {{n}_{5}} + {{n}_{6}} = 0, \\ {{n}_{1}} + 2{{n}_{2}} + {{n}_{6}} = 0. \\ \end{gathered} \right\}$

Решая систему уравнений (3) относительно n₃, n₄, n₅, находим

${{n}_{1}} = --2{{n}_{4}}--{{n}_{6}};\quad {{n}_{2}} = {{n}_{4}}--{{n}_{6}}--{{n}_{7}};\quad {{n}_{5}} = --{{n}_{3}}--{{n}_{6}}.$

Следовательно, имеем выражение

(4)

$\Pi = u_{0}^{{ - 2{{n}_{4}} - {{n}_{6}}}}{{d}^{{{{n}_{4}} - {{n}_{6}} - {{n}_{7}}}}}{{(\rho _{т}^{{}} - \rho )}^{{{{n}_{3}}}}}{{а}^{{n{}_{4}}}}\rho _{{}}^{{ - {{n}_{3}} - {{n}_{6}}}}{{\eta }^{{{{n}_{6}}}}}{{l}^{{{{n}_{7}}}}}) = {{\left( {\frac{{\Delta \rho }}{\rho }} \right)}^{{{{n}_{3}}}}}{{\left( {\frac{1}{{ad{{u}_{0}}}}} \right)}^{{{{n}_{4}}}}}{{\left( {\frac{\eta }{{d{{u}_{0}}\rho }}} \right)}^{{{{n}_{6}}}}}{{\left( {\frac{l}{d}} \right)}^{{{{n}_{7}}}}}.$

Числа: n₃; n₄; n₆, выраженные через остаток, можно исключить из расчета

(5)

$\left. \begin{gathered} - 3{{n}_{3}} + {{n}_{4}} - {{n}_{6}} + {{n}_{7}} = 0, \\ {{n}_{3}} + {{n}_{6}} = 0, \\ 2{{n}_{2}} + {{n}_{6}} = 0. \\ \end{gathered} \right\}$

Решая систему уравнений (5) относительно n₃, находим

${{n}_{{\text{4}}}} = \frac{{{{n}_{3}}}}{2};\quad {{n}_{6}} = - {{n}_{3}};\quad {{n}_{{\text{7}}}} = \frac{{3{{n}_{3}}}}{2}.$

Тогда уравнение (4) примет вид

$\Pi = {{\left( {\frac{{\Delta \rho }}{\rho }} \right)}^{{{{n}_{3}}}}}{{\left( {\frac{1}{{ad{{u}_{0}}}}} \right)}^{{{{n}_{4}}}}}{{\left( {\frac{\eta }{{d{{u}_{0}}\rho }}} \right)}^{{{{n}_{6}}}}}{{\left( {\frac{l}{d}} \right)}^{{{{n}_{7}}}}} = {{\left( {\frac{{\Delta \rho }}{\rho }} \right)}^{{{{n}_{3}}}}}{{\left( {\frac{1}{{ad{{u}_{0}}}}} \right)}^{{\frac{1}{2}{{n}_{3}}}}}{{\left( {\frac{\eta }{{d{{u}_{0}}\rho }}} \right)}^{{ - {{n}_{3}}}}}{{\left( {\frac{l}{d}} \right)}^{{\frac{3}{2}{{n}_{3}}}}} = \frac{{\Delta \rho }}{\eta }\sqrt {\frac{l}{{a{{d}^{2}}}}} .$

Отсюда получаем зависимость ускорения от остальных параметров

$a = \sqrt {\frac{{\Delta \rho }}{{\eta d}}{{l}^{{3/2}}}} .$

В процессе обработки поверхности, термоабразивная струя в плоскостях α, β, γ сообщает начальную скорость u₀, в среднем проходит расстояние длиной l. Поэтому условно за среднюю скорость частицы в потоке примем скорость u_ср, с которой движется частица в конце пути. Учитывая, что в данном случае u = u₀ – аt, t = $t = {v}{\text{/}}60$, тогда

(6)

${{u}_{{{\text{ср}}}}} = \frac{l}{{216}}\left( {{{{60}}^{2}} - {v}\sqrt {\frac{{\Delta \rho }}{{\eta d{{l}^{{1/2}}}}}} } \right) \times {{10}^{{ - 3}}},$

где ${v}$ – скорость вращения поверхности детали, с^–1.

Анализ выражения (6) позволяет наглядно отобразить зависимость скорости частиц от их размера и плотности материала (рис. 2). При этом скорость вращения поверхности детали ${v}$ = 30 с^–1, длина поверхности детали l = 0.25 м, плотность материала детали ρ = 7800 кг/м³ и ударная вязкость материала детали η = 15 кг м/см² приняты за постоянные величины.

Рис. 2.

Зависимость скорости абразивной частицы от ее размера и плотности.

Следовательно, скорость частицы в термоабразивном потоке возрастает с увеличением размера и уменьшается с увеличением плотности материала частицы. Это объясняется тем, что кинетической энергии частицы из более плотного материала, для преодоления силы тяжести и сопротивления потоку недостаточно. В свою очередь менее плотные частицы независимо от их размера движутся вместе с потоком, активно взаимодействуя с поверхностью детали, несмотря на то, что тяжелые частицы при взаимодействии с поверхностью детали не передают достаточной энергии для снятия металла с поверхности.

Принимая за среднюю скорость движения частицы, усредненную величину по ее диаметру и плотности, за счет упрощенной модели и погрешности, находим суммарную скорость в момент ее взаимодействия с поверхностью детали

(7)

$V = z{{u}_{{{\text{ср}}}}}\cos (\beta + \gamma ),$

где u_ср – скорость частицы (u_ср = 1.13 м/с); α – угол наклона поверхности детали (α = 35°); β – угол наклона абразивной частицы; γ – угол наклона результирующей скорости к плоскости детали.

Из выражения (7) находим результирующую скорость точки на плоскости

(8)

$z = {{{v}}_{{\text{р}}}}{{{v}}_{{\text{л}}}}\cos (90 + \alpha );\quad {{{v}}_{{\text{р}}}} = \frac{{2\pi R60}}{\upsilon };\quad {{{v}}_{{\text{л}}}} = \frac{{60l}}{\upsilon },$

где z – результирующая скорость точки на плоскости; R – средний радиус частицы (R = 0.002 м); ${{{v}}_{{\text{р}}}}$ – радиальная скорость точки на плоскости детали; ${{{v}}_{{\text{л}}}}$ – линейная скорость точки на плоскости детали; α – угол наклона поверхности детали (α = 35°).

Выражая угол γ через косинус угла α, получили выражение

(9)

$\gamma = {\text{arcos}}\left( {\frac{{{{{v}}_{{\text{р}}}}\cos \alpha }}{V}} \right) + \alpha = {\text{arcos}}\left( {\frac{{\upsilon \cos \alpha }}{{60l\cos (90 + \alpha )}}} \right) + \alpha .$

Подставив выражения (8) и (9) в уравнение (7), получим выражение

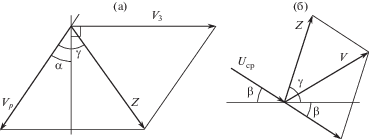
$V = {{u}_{{{\text{ср}}}}}2l\pi R{{\left( {\frac{{60}}{\upsilon }} \right)}^{2}}\cos \left( {\beta + \alpha + {\text{arcos}}\left( {\frac{{\upsilon \cos \alpha }}{{60l}}} \right)} \right).$

Рис. 3.

Схема сложения векторов скоростей: (а) – результирующая скорость z точки на плоскости; (б) – сумма скоростей абразивной частицы V.

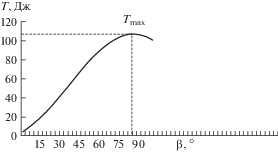
На основании уравнения (1), принимая m = const, провели расчеты подводимой энергии в момент соударения абразивной частицы с поверхностью детали. Расчеты выполнены с использованием инженерного математического обеспечения Mathcad Prime 6.0, которое позволяет выполнять, анализировать инженерные расчеты и обмениваться ими [11]. Результаты расчетов представлены в табл. 1. Анализ зависимости подводимой энергии абразивной частицы от угла наклона термоабразивной струи позволяет предположить, что процесс максимального снятия металла при термоабразивном воздействии струи на обрабатываемую поверхность будет происходить при углах наклона, лежащих в интервале от 75° до 80°.

Таблица 1.

Изменение подводимой энергии в момент соударения абразивной частицы с поверхностью детали

Т, Дж	7.89	14.69	23.18	27.94	38.25	49.21
β, °	5	10	15	20	25	30

Т, Дж	54.79	65.84	76.34	81.24	90.08	97.31
β, °	35	40	45	50	55	60

Т, Дж	100.22	104.47	106.49	106.63	105.16	101.42
β, °	65	70	75	80	85	90

На основании данных, представленных в табл. 1, построили зависимость подводимой энергии от угла наклона абразивной частицы (рис. 4).

Рис. 4.

Зависимость подводимой энергии абразивной частицы от угла наклона термоабразивной струи.

Тепловую энергию Γ при ударе с частицей можно записать выражением

$Т = \Gamma + {{Т}_{{\text{к}}}};\quad \Gamma = е + \lambda М,$

где е – тепловая энергия, перешедшая в обрабатываемую поверхность, Дж; λ – удельная теплота плавления стали, (λ = 84 кДж/кг); М – масса металла на участке, которая подверглась нагреву, кг; Т_к – кинетическая энергия частицы, которая определяется из системы уравнений

(10)

$\left. \begin{gathered} V = {{V}_{2}} + \Gamma , \hfill \\ Т = \Gamma + \frac{{V_{2}^{2}}}{2}, \hfill \\ \end{gathered} \right\}$

где V₂ – скорость отскока частицы, м/с.

Решая систему уравнений (10) относительно V₂, получим выражение

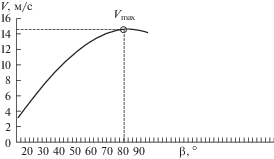
${{V}_{2}} = 1 - \sqrt {\frac{1}{4} + 2Т - V} ;\quad {{Т}_{{\text{к}}}} = \frac{{{{{\left( {1 - \sqrt {\frac{1}{4} + 2Т - V} } \right)}}^{2}}}}{2}.$

Анализ графика, представленного на рис. 4, показывает, что максимальная энергия Т = 106.63 Дж будет подводиться при угле наклона относительно поверхности детали β = 80°. Соответствующая этим параметрам сумма скоростей частиц в зависимости от угла наклона в момент соударения составит V = 14.6 м/с (рис. 5). Тогда масса удаленного металла термоабразивной струей с поверхности детали для этих условий составит

$\begin{gathered} М = \frac{{0.76\left( {Т - {{{\left( {1 - \sqrt {\frac{1}{4} + 2Т - V} } \right)}}^{2}}} \right)}}{\lambda } = \\ = \frac{{0.76\left( {106.63 - {{{\left( {1 - \sqrt {\frac{1}{4} + 2 \times 106.63 - 14.6} } \right)}}^{2}}} \right)}}{{84}} \approx 0.19{\text{ г}}{\text{.}} \\ \end{gathered} $

Рис. 5.

Зависимость суммарной скорости V от угла наклона абразивной частицы β.

При плотности углеродистых качественных сталей ρ = 7800 кг/м³ средний объем съема металла с поверхности детали составит

${{V}_{{{\text{ср}}}}} = \frac{{0.19}}{{78 \times {{{10}}^{5}}}} = 2.40 \times {{10}^{{ - 8}}}\;{{{\text{м}}}^{3}} = 24.00\;{\text{м}}{{{\text{м}}}^{3}}.$

Материал, из которого изготовлена деталь, становится более мягким и при дальнейших соударениях с абразивными частицами снимается. Таким образом, можно предположить, что процесс снятия металла при термоабразивном воздействии струи происходит в две стадии: стадия нагрева поверхности детали и стадия удаления.

Выводы. Результаты теоретических исследований механизма удаления металла с поверхности детали при термоабразивном воздействии показывают, что отделение частицы металла достаточно сложный, комплексный процесс, который определяется, с одной стороны, условиями воздействия термоабразивной струи, а с другой – структурным состоянием и свойствами материалов из которых изготовлена деталь. При этом большая роль при выборе материалов отводится сталям, их термообработке и легирующим добавкам.

Список литературы

Бриджмен П.В. Анализ размерностей / Под ред. акад. С.И. Вавилова. Ленинград; М.: Гос. техн.-теоретич. изд-во, 1934. 120 с.
Карцев С.В., Ерофеев М.Н., Карцева И.В. и др. Способ подготовки поверхности для нанесения износостойких покрытий. РФ Патент 2737909, 2020.
Кравченко И.Н. Ресурсосберегающие плазменные технологии при ремонте перерабатывающего оборудования. М.: ИНФРА-М, 2021. 200 с. https://doi.org/10.12737/1083289
Математическое моделирование; https://studopedia.su/18_3746_matematicheskoe-modelirovanie.html
Некоторые обзорные работы и первоисточники по истории пи-теоремы и теории подобия; http://gidropraktikum.narod.ru, http://gidropraktikum.narod.ru/pi-theorem-history.htm
Математическое подобие объектов. Обзор способов определения коэффициентов подобия; https://studopedia.su https://studopedia.su/18_19391_matematicheskoe-podobie-ob-ektov-obzor-sposobov-opredeleniya-koeffitsientov-podobiya.html
Пузряков А.Ф. Теоретические основы технологии плазменного напыления. Учеб. пособие. М.: МГТУ им. Н.Э. Баумана, 2008. 360 с.
Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1981. 448 с.
Yan J., Liu L., Mao Z. Effect of Spraying Powders Size on the Microstructure, Bonding Strength, and Microhardness of MoSi₂ Coating Prepared by Air Plasma Spraying // Journal of Thermal Spray Technology. 2014. V. 23. Is. 6. P. 934.
Ramachandran C.S., Balasubramanian V., Ananthapadmanabhan P.V. Multiobjective Optimization of Atmospheric Plasma Spray Process Parameters to Deposit Yttria-Stabilized Zirconia Coatings Using Response Surface Methodology // Journal of Thermal Spray Technology. 2011. V. 20. Is. 3. P. 391.
Mathcad Express – бесплатный математический редактор // https://habr.com/ru https://habr.com/ru/company/nerepetitor/blog/247999/

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал