Проблемы машиностроения и надежности машин, 2021, № 4, стр. 70-80
Исследование аэроупругих явлений корпуса и тонкостенных конструкций беспилотных ЛА при больших сверхзвуковых скоростях
Ф. А. Абдухакимов 1, А. В. Быков 2, В. В. Веденеев 1, Л. Р. Гареев 1, *, В. А. Нестеров 3
1 Московский государственный университет имени М.В. Ломоносова
Москва, Россия
2 Государственное машиностроительное конструкторское бюро “Вымпел” им. И.И. Торопова
Москва, Россия
3 Московский авиационный институт
Москва, Россия
* E-mail: gareev.lr@yandex.ru
Поступила в редакцию 11.06.2020
После доработки 17.02.2021
Принята к публикации 24.02.2021
Аннотация
Флаттер беспилотных летательных аппаратов на гиперзвуковых скоростях является одной из малоизученных проблем, стоящих перед разработчиками гиперзвуковых аппаратов. Современные методы расчета аэроупругой устойчивости либо позволяют решать упрощенные варианты реальных задач (например, без учета физико-химических явлений), либо требуют большой вычислительной мощности. В настоящей статье описывается методика расчета сверх- и гиперзвукового флаттера летательного аппарата с использованием стандартного инженерного программного обеспечения и дополнительных разработанных программных модулей. Дано обоснование необходимости уточнения существующих методик расчета аэроупругости летательных аппаратов с учетом реальной геометрии конструкции и с возможностью учета физико-химических процессов, происходящих в воздухе при движении тел с большой скоростью. Разработаны теоретические положения расчета аэроупругой устойчивости с учетом этих факторов и приведены три примера расчета аэроупругой устойчивости модельных объектов.
При полете летательных аппаратов с высокими скоростями, в том числе сверхзвуковыми и гиперзвуковыми скоростями, может возникать явление флаттера различных элементов конструкции летательных аппаратов – крыльев, рулей, корпуса, панелей обшивки [1]. Используемые в настоящее время инженерные подходы к расчету аэроупругой устойчивости зачастую используют упрощенные подходы: идеализация рулей и корпуса пластинами и цилиндрическими оболочками, которые обтекаются с нулевым углом атаки. В действительности, геометрия внешних обводов тела обычно является более сложной, а режимы полета включают ненулевые углы атаки, но эти особенности не учитываются в расчетах флаттера. Особенность гиперзвукового потока заключается в том, что при этих скоростях воздух после головной ударной волны находится в неравновесном состоянии, и существенными факторами, влияющими на обтекание, являются процессы диссоциации и рекомбинации молекул, сопровождающиеся различными химическими реакциями. При таких условиях граница устойчивости к флаттеру должна определяться с учетом химических реакций и кинетических процессов в набегающем потоке воздуха. Эти эффекты до настоящего времени остаются практически неисследованными и не учитываются в практике инженерных расчетов.
В то же время, в России и за рубежом проектируются летательные аппараты с полетными числами Маха М = 6…15, внешние обводы которых имеют сложную форму, и обтекание которых может сопровождаться указанными выше химическими превращениями. Для достижения больших скоростей полета конструкция таких аппаратов должна иметь высокое весовое совершенство, которое обеспечит размещение на гиперзвуковых летательных аппаратах (ГЗЛА) необходимого для решения боевых задач бортового оборудования и боевой части. Конструкции ГЗЛА могут иметь тонкостенные панели обшивки и упругое оперение, и, следовательно, они могут быть подвержены флаттеру и возможным разрушениям от него. Расчеты границ устойчивости к флаттеру таких аппаратов на основе упрощенных методик могут давать количественно неверные предсказания границ устойчивости [2]. Таким образом, высока актуальность разработки более совершенной методики расчета аэроупругой устойчивости, учитывающей как реальную геометрию внешних обводов тела, так и химические превращения в воздухе, и создания на ее основе программных модулей и библиотек для расчета флаттера в сверхзвуковом потоке.
Методика расчета аэроупругой устойчивости. Выведем систему уравнений движения аэроупругой системы в обобщенных координатах из системы дифференциальных уравнений движения Лагранжа [3]
Для получения выражений для линеаризованных обобщенных сил рассмотрим элементарную работу ${{\delta }}W$, совершаемую аэродинамическим давлением на элементарном приращении обобщенных координат ${{\delta }}{{u}_{j}}$
Из вариационного принципа Даламбера–Лагранжа [3] следует, что
Таким образом, вектор-столбец линеаризованных обобщенных аэродинамических сил можно представить в виде произведения матрицы
Выражения для кинетической T и потенциальной U энергии линейно упругого тела в обобщенных координатах имеют вид
Здесь также учтена матрица конструкционного демпфирования $\hat {D}$, которую можно задать при известных значениях коэффициентов демпфирования по каждому собственному колебанию.
Анализ аэроупругой устойчивости в рассмотренных ниже примерах проводился для ненагруженного состояния конструкции (нулевой угол атаки и нулевой угол отклонения рулей) в силу рассмотрения движения достаточно жестких тел сравнительно небольших размеров, что, однако, не ограничивает общность методики. Для вычисления нагрузок, действующих со стороны потока воздуха на конструкцию, используется численное решение уравнений газовой динамики (CFD). Решается система уравнений Навье–Стокса и энергии для вязкого теплопроводного газа.
Уравнение неразрывности $\frac{{\partial {{\rho }}}}{{\partial t}} + \nabla \cdot \left( {{{\rho }}U} \right) = 0$.
Уравнения Навье–Стокса $\frac{{\partial (\rho U)}}{{\partial t}}\, + \,\nabla \, \cdot \,(\rho U\, \otimes U) = - \nabla p\, + \,\nabla \, \cdot \,\tau $, где ${{(U \otimes U)}_{{ij}}}$ = ${{(U{{U}^{T}})}_{{ij}}}$ = = ${{U}_{i}}{{U}_{j}}$, и компоненты тензора τ выражаются как ${{\tau }_{{ij}}}$ = ${{\mu }}\left( {{{\nabla }_{j}}{{U}_{i}} + {{\nabla }_{i}}{{U}_{j}} - \frac{2}{3}{{{{\delta }}}_{{ij}}}\left( {\nabla \cdot U} \right)} \right)$, а ${{{{\delta }}}_{{ij}}}$ – символ Кронекера.
Уравнение энергии, записанное через полную энтальпию
Система уравнений решается методом контрольных объемов. Получение характеристик установившегося течения проводится методом установления. В случае, когда химическими реакциями в потоке можно пренебречь (число Маха не превышает пяти), система уравнений замыкается уравнением состояния совершенного газа. В случае учета химических реакций в воздухе при гиперзвуковых скоростях полета, эта система уравнений рассматривается для смеси реагирующих компонент и дополняется системой уравнений химических реакций [4].
Получив уравнения движения аэроупругой системы и вычислив матрицу ${{\hat {K}}_{a}}$, решается задача на комплексные собственные значения. Представляя u как $u = C{{e}^{{{{\lambda }}t}}}$, находим
В результате получаем набор N собственных значений λ. Критерием устойчивости является условие $\operatorname{Re} ~\lambda \leqslant 0$. При наличии вещественного положительного собственного значения имеется дивергенция, комплексного собственного значения с положительной вещественной частью – флаттер.
Практическая реализация методики. В настоящей статье описывается методика расчета флаттера, при которой обобщенные аэродинамические силы вычисляются на основе численного моделирования обтекания (CFD) реальной геометрии конструкции с возможностью учета происходящих в воздухе химических реакций. Как показано, в предыдущем разделе, в силу больших скоростей полета и относительно небольших размеров рассматриваемых объектов, предполагается, что обтекание колеблющейся конструкции квазистационарно. Конкретная реализация методики основана на использовании двух коммерческих программных пакетов, используемых в инженерной практике: MSC.Nastran [5, 6] – для расчета собственных частот и форм колебаний конструкции в пустоте и для решения задачи на собственные значения связанной аэроупругой системы и Ansys CFX [7] – для решения задачи о квазистационарном обтекании конструкции. Для интеграции этих двух программных пакетов, вычисления обобщенных аэродинамических сил, формирования матрицы аэродинамической жесткости и обработки результатов разработаны дополнительные программные модули.
Блок-схема проведения расчетов показана на рис. 1. Собственные формы и частоты колебаний (как корпусные, так и рулевых поверхностей) рассчитываются в MSC.Nastran стандартным методом конечных элементов (решатель SOL 103) и с использованием разработанного программного модуля передаются в газодинамический пакет Ansys CFX. В нем рассчитывается обтекание конструкции при деформациях корпуса по собственным формам. Далее, используя второй разработанный модуль, вычисляются обобщенные аэродинамические силы, формирующие матрицу аэродинамической жесткости. Эта матрица передается в MSC.Nastran для расчета комплексных собственных частот колебаний связанной аэроупругой системы (решатель SOL 110), который проводится методом Бубнова–Галеркина (в терминологии Nastran – “в модальных координатах”), что требует сравнительно небольшого числа учитываемых собственных форм при вычислении обобщенных аэродинамических сил. Согласно теории, критерием неустойчивости (дивергенции или флаттера) является наличие собственной частоты с положительной вещественной частью.
Примеры применения. С помощью разработанной методики были исследованы три объекта, а также проведено сравнение результатов с данными, полученными из натурных экспериментов.
На рис. 2а, б представлена геометрия первого исследуемого объекта – беспилотного маневренного ЛА. Все расчеты для данной модели были проведены для параметров полета на высоте 25 км и числе Маха М = 5. Описание низших собственных форм колебаний модели приведено в табл. 1 и на рис. 3. В расчетах учитывались две корпусные собственные формы колебаний (первая и вторая изгибные формы с номерами 8 и 10), а также трех форм колебаний рулей (изгибная, изгибно-крутильная и вращательная – номера 20, 28, 30). Стоит отметить, что в табл. 1 несколько частот соответствуют одной форме, поскольку соответствующая собственная форма реализуется на различных рулях, а малое отличие в значениях частот обусловлено несимметричным расположением бортового оборудования и полезной нагрузки.
Таблица 1.
Собственные формы. Первая модель
| Форма | Частота, Гц | Тип собственной формы | Форма | Частота, Гц | Тип собственной формы |
|---|---|---|---|---|---|
| 1 | 0 | Незакрепленное перемещение | 16 | 179.19 | Рулевая, 1-я изгибная |
| 2 | 0 | Незакрепленное перемещение | 17 | 185.07 | Рулевая, 1-я изгибная |
| 3 | 0 | Незакрепленное перемещение | 18 | 197.42 | Рулевая, 1-я изгибная |
| 4 | 0 | Незакрепленное перемещение | 19 | 201.39 | Рулевая, 1-я изгибная |
| 5 | 0 | Незакрепленное перемещение | 20 | 201.80 | Рулевая, 1-я изгибная |
| 6 | 0 | Незакрепленное перемещение | 21 | 285.09 | Корпусная, продольная |
| 7 | 38.98 | Корпусная, 1-я изгибная | 22 | 325.78 | Корпусная, 3-я изгибная |
| 8 | 38.98 | Корпусная, 1-я изгибная | 23 | 325.78 | Корпусная, 3-я изгибная |
| 9 | 97.79 | Корпусная, 2-я изгибная | 24 | 400.03 | Корпусная, смешанная |
| 10 | 97.90 | Корпусная, 2-я изгибная | 25 | 400.03 | Корпусная, смешанная |
| 11 | 117.16 | Рулевая, изгибная в плоскости руля | 26 | 444.81 | Корпусная, смешанная |
| 12 | 122.77 | Рулевая, изгибная в плоскости руля | 27 | 444.81 | Корпусная, смешанная |
| 13 | 123.16 | Рулевая, изгибная в плоскости руля | 28 | 444.93 | Рулевая, изгибно-крутильная |
| 14 | 124.02 | Рулевая, изгибная в плоскости руля | 29 | 483.48 | Рулевая, вращательная |
| 15 | 179.14 | Рулевая, 1-я изгибная | 30 | 483.64 | Рулевая, вращательная |
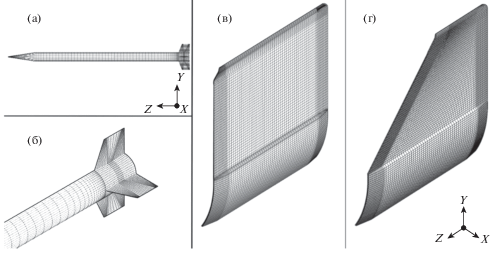
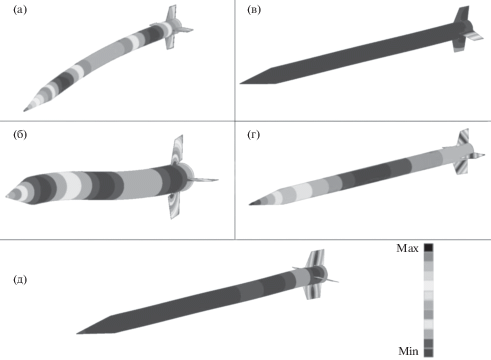
Рис. 3.
Собственные формы колебаний первой модели. Масштаб увеличен в 15 раз: (а) – мода 8; (б) – мода 10; (в) – мода 20; (г) – мода 28; (д) – мода 30.
Расчет комплексных собственных значений в модуле SOL110 MSC.Nastran показал отсутствие флаттера (табл. 2).
Таблица 2.
Результаты расчета собственных значений. Первая модель. М = 5; Н = 25 км
| Мода | Δ | ω, Гц | Мода | Δ | ω, Гц |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 16 | 0 | 179.19 |
| 2 | 0 | 0 | 17 | 0 | 185.07 |
| 3 | 0 | 0 | 18 | 0 | 197.42 |
| 4 | 0 | 0 | 19 | 0 | 201.39 |
| 5 | 0 | 0 | 20 | 0 | 201.83 |
| 6 | 0 | 0 | 21 | 0 | 285.09 |
| 7 | 0 | 38.97 | 22 | 0 | 325.78 |
| 8 | 0 | 38.98 | 23 | 0 | 325.78 |
| 9 | 0 | 97.79 | 24 | 0 | 400.03 |
| 10 | 0 | 97.90 | 25 | 0 | 400.03 |
| 11 | 0 | 117.16 | 26 | 0 | 444.81 |
| 12 | 0 | 122.77 | 27 | 0 | 444.81 |
| 13 | 0 | 123.16 | 28 | 0 | 444.95 |
| 14 | 0 | 124.02 | 29 | 0 | 483.48 |
| 15 | 0 | 179.14 | 30 | 0 | 483.67 |
Об этом свидетельствуют нулевые значения аэродинамического демпфирования $\Delta = - \operatorname{Re} \left( \lambda \right)$, приведенные для всех рассчитанных физических частот колебаний $\omega = \frac{{\operatorname{Im} \left( \lambda \right)}}{{2\pi }}$, которые практически не отличаются от частот колебаний в пустоте. Это вызвано достаточно большими собственными частотами колебаний рулей и большой высотой полета на рассмотренном режиме (25 км), при которой аэродинамическое воздействие потока на ракету мало. Результаты расчета подтверждены натурными испытаниями.
На рис. 2в, г представлены геометрии второго и третьего исследуемого объекта – оперение маневренного ЛА. Согласно экспериментальным данным, использование трапециевидного руля (рис. 2г) не вызывало флаттер на различных расчетных режимах полета. В то же время замена трапециевидной геометрии оперения на прямоугольную (рис. 2в) приводила к флаттеру. Расчеты по предлагаемой в этой статье методике подтверждают экспериментальные результаты. Все расчеты проводились с параметрами, соответствующими нулевой высоте над уровнем моря.
На рис. 4 изображены, а в табл. 3 описаны полученные собственные формы колебания второй модели в пустоте.
Рис. 4.
Собственные формы колебаний второй модели. Масштаб увеличен в 15 раз. На (а)–(г) изображены с 1 по 4 моды соответственно.
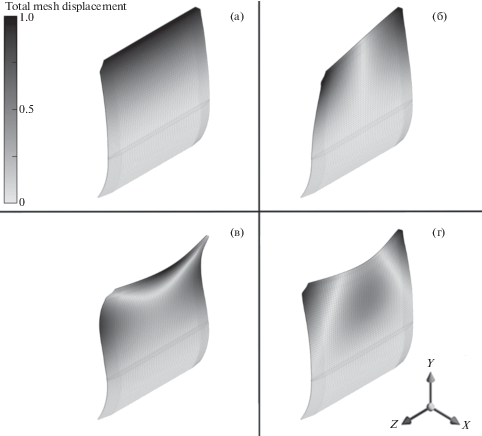
Таблица 3.
Собственные формы. Вторая модель
| Мода | Частота, Гц | Тип собственной формы |
|---|---|---|
| 1 | 87.40 | 1-я изгибная |
| 2 | 156.97 | 1-я крутильная |
| 3 | 376.72 | 2-я изгибная |
| 4 | 436.55 | пластинчатая |
В табл. 4 приведены полученные по результатам расчета согласно методике результаты для оперения прямоугольной формы. Сначала был проведен расчет для числа Маха М = 2.5, по результатам которого был сделан вывод о флаттере связанного типа по второй форме на этом режиме полета. Далее были проведены расчеты для М = 2 и М = 1.5 (отметим, что в последнем случае предположение о квазистационарности потока заведомо неверно, и этот расчет представляет чисто академический интерес). Полученные значения коэффициентов аэродинамического демпфирования также свидетельствуют о наличии того же типа флаттера.
Таблица 4.
Результаты расчета комплексных собственных значений. Вторая модель. H = 0 км. Слева направо: М = 2.5; М = 2; М = 1.5
| Мода | Δ, Гц | ω, Гц | Мода | Δ, Гц | ω, Гц | Мода | Δ, Гц | ω, Гц |
|---|---|---|---|---|---|---|---|---|
| 1 | 308 | 172.55 | 1 | 244 | 145.22 | 1 | 171 | 114.0 |
| 2 | –308 | 172.55 | 2 | –244 | 145.22 | 2 | –171 | 114.0 |
| 3 | 0 | 375.51 | 3 | 0 | 386.35 | 3 | 0 | 378.1 |
| 4 | 0 | 432.07 | 4 | 0 | 424.23 | 4 | 0 | 408.6 |
Аналогичные расчеты были проведены для трапециевидной модели оперения. На рис. 5 изображены, а в табл. 5 описаны полученные собственные формы модели. Сначала был проведен расчет для М = 2, затем на М = 6 (табл. 6). При этом Δ остался равен нулю, что указывает на отсутствие флаттера.
Рис. 5.
Собственные формы колебаний третьей модели. Масштаб увеличен в 15 раз. На (а)–(г) изображены с 1 по 4 моды соответственно.
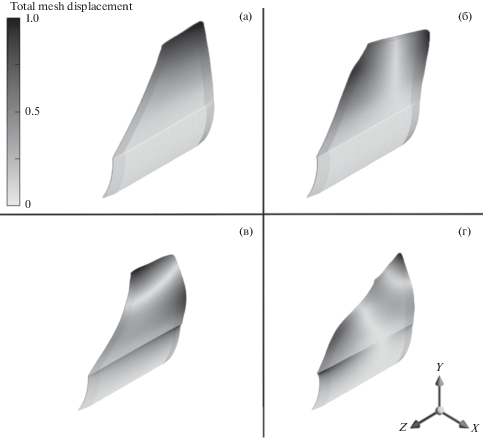
Таблица 5.
Собственные формы. Третья модель
| Мода | Частота, Гц | Тип собственной формы |
|---|---|---|
| 1 | 145.20 | 1-я изгибная |
| 2 | 394.85 | 1-я крутильная |
| 3 | 585.12 | 2-я изгибная |
| 4 | 887.48 | 2-я крутильная |
Таблица 6.
Результаты расчета комплексных собственных значений. Третья модель. Н = 0 км. Слева направо: М = 2; М = 6
| Мода | Δ, Гц | ω, Гц | Мода | Δ, Гц | ω, Гц |
|---|---|---|---|---|---|
| 1 | 0 | 168.02 | 1 | 0 | 254.38 |
| 2 | 0 | 389.10 | 2 | 0 | 409.99 |
| 3 | 0 | 593.83 | 3 | 0 | 606.13 |
| 4 | 0 | 880.11 | 4 | 0 | 888.44 |
Заключение. В статье приведена теория и методика расчета флаттера конструкций летательных аппаратов при больших скоростях полета с учетом реальной геометрии конструкции и возможности учета особенностей гиперзвукового потока (химических превращений, вязких эффектов и др.). Описана практическая реализация методики проведения расчетов с использованием разработанных программных модулей и с частичным использованием стандартного инженерного ПО. Приведены примеры расчета флаттера модельных конструкций летательных аппаратов, результаты которых соответствуют экспериментальным.
Описанную методику можно применить при исследовании флаттера других летательных аппаратов, а также их конструкционных составляющих. Методику можно использовать совместно с другими, в т.ч. российскими, программными комплексами путем разработки дополнительных модулей, обеспечивающих связи “упругого” и “газодинамического” решателя и проведения промежуточных вычислений.
Список литературы
Bisplinghoff R.L., Ashley H., Halman R.L. Аэроупругость. Москва. Издательство иностранной литературы, 1958.
Vedeneev V.V., Nesterov V.A. Effect of nonequilibrium reacting flow on flutter at hypersonic flight speed // AIAA Journal, 2019. V. 57. № 5. P. 2222.
Маркеев А.П. Теоретическая механика. М.: Черо, 1999. 572 с.
Kang S.W., Jones W.L., Dunn M.G. Theoretical and Measured Electron-Density Distributions at High Altitudes // AIAA Journal. 1973. V. 11. № 2. P. 141.
MSC. Nastran Quick Reference Guide.
MSC. Nastran Dynamic Analysis User’s Guide.
Documentation for ANSYS CFX 12.1. SAS IP, Inc., 2009.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин