1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 4, 2021

Проблемы машиностроения и надежности машин, 2021, № 4, стр. 37-44

Анализ напряженно-деформированного состояния композиционных цилиндрических оболочек на основе уточненной теории с учетом пьезоэлектрического эффекта

В. В. Фирсанов 1, Л. Х. Нгуен 1, 2, *

1 Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

2 Государственный технический университет им. Ле Куи Дона
Ханой, Социалистическая Республика Вьетнам

* E-mail: lehung.mai@mail.com

Поступила в редакцию 30.09.2020
После доработки 07.04.2021
Принята к публикации 26.04.2021

Полный текст (PDF)

Аннотация

В настоящей статье представлена уточненная математическая модель напряженно-деформированного состояния многослойных композиционных цилиндрических оболочкек с учетом пьезоэлектрического эффекта. Перемещения и электрический потенциал оболочки представляются в виде полиномов по нормальной координате на две степени выше по отношению к классической теории типа Кирхгофа–Лява. Математическая модель электромеханического состояния композиционных оболочек получена с помощью вариационного принципа Лагранжа. Сформулированная краевая задача электроупругости решается путем сведения трехмерных уравнений к двумерным. Рассматривается пример расчета напряженного состояния типа “погранслой” композиционных цилиндрических оболочек с учетом пьезоэлектрического эффекта с симметричным и ассиметричным распределениями слоев под действием произвольной механической и электрической нагрузок.

Ключевые слова: композиционная цилиндрическая оболочка, уточненная теория, пьезоэлектрический эффект, напряженное состояние “погранслой”, электроупругость, электромеханическое состояние

На сегодняшний день большинство современных технических устройств, использующих пьезоэффект, создаются на базе однослойных или многослойных композиционных элементов. Это связано с тем, что такие устройства обладают низкой массой, высокой механической прочностью, повышенной чувствительностью и температурной стабильностью, высокой эффективностью преобразования электрической энергии в механическую, низкой себестоимостью и простотой конструкции. Особенно, пьезоэффекты активно исследуются и применяются в авиационных и космических отраслях. Композиционные пьезоэлементы используются на летательных аппаратах (ЛА) в виде корпусных элементов, панелей, в устройствах системы активного управления для адаптипных конструкций [1]. С помощью различных сенсоров и актюаторов, изготовленных из smart-материалов, ЛА можно обеспечить необходимое распределение аэродинамических нагрузок по размаху упругого крыла и получить оптимальные значения аэродинамических коэффициентов, уменьшить аэродинамические нагрузки на при маневрах и порывах ветра, подавить флаттер, снизить уровень вибраций [2]. Следовательно, использование композиционных пьезоэлементов помогает ЛА при гашении аэроупругих колебаний за счет повышения качества аэродинамики и эффективного управления их деформациями.

Основными расчетными схемами элементов конструкций ЛА являются тонкие пластинки и оболочки [3], находящиеся под действием различных факторов. В настоящее время инженерные расчеты напряженно-деформированного состояния (НДС) указанных элементов конструкций ЛА базируются на результатах классической теории пластин и оболочек типа Кирхгофа–Лява [4], Тимошенко–Рейсснера [5]. В работах [6–8] и др. показано, что расчеты по классической теории не дают удовлетворительного соответствия с практикой из-за наличия дополнительных напряжений типа “погранслой” при исследовании НДС не только изотропных пластин, оболочек в узких краевых зонах искажения, но и оболочек, выполненных из анизотропных, в том числе композиционных материалов.

Вместе с тем, технический прогресс и внедрение новых технологий предъявляют повышенные требования к более точным моделям для описания поведения пластин и оболочек. В последнее время предложены новые методы расчета НДС тонкостенных конструкций. Численные методы, основанные на методе конечных элементов (МКЭ), используются [9] в виде известных программных пакетов Ansys, Nastran, ACELAN и др. для моделирования НДС конструкции на электронно-вычислительных машинах (ЭВМ). Среди аналитических подходов можно назвать: теории сдвиговых деформаций первых, третьих и высших порядков (FSDT, TSDT и HSDT) [9], методы асимптотического интегрирования дифференциальных уравнений трехмерной теории упругости [10], метод простых итераций [11], метод конечных разностей [7], метод собственных функций [12] и др. Один из подходов к построению уточненной теории, называемый в [13] энергетически согласованным, заключается в разложении искомых перемещений в полиноминальные ряды по нормальной координате и последующем применении вариационного принципа Лагранжа.

В настоящей статье в рамках указанного подхода [13] разработана уточненная математическая модель НДС многослойной композиционной цилиндрической оболочки с учетом пьезоэлектрического эффекта с симметричным и ассиметричным распределениями слоев под действием произвольной механической и электрической нагрузок. Указанная математическая модель, по сравнению с классической теорией, дает более достоверные результаты, так как позволяет учесть НДС типа “погранслой” вблизи жестко закрепленных краев пластин и оболочек.

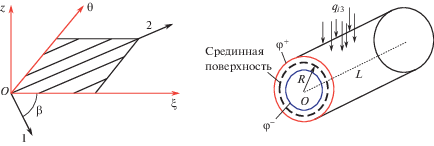
Электромеханическое состояние композиционной цилиндрической оболочки с учетом пьезоэффекта. Композиционная оболочка рассматривается как трехмерное твердое тело, отнесенное к триортогональной криволинейной системе координат $\xi $, $\theta $, $z$ и находится под действием произвольных механических нагрузок ${{q}_{{i3}}} = q_{{i3}}^{ \pm }(\xi ,\theta )$, ($i = 1,2,3$) и электрических потенциалов ${{\varphi }_{i}} = {{\varphi }^{ \pm }}(\xi ,\theta )$ (рис. 1). Оболочка имеет длину L, толщину 2h, радиус R и состоит из N слоев. Угол армирования каждого слоя k обозначим через ${{\beta }_{k}}$.

Рис. 1.

Пьезокомпозиционная цилиндрическая оболочка.

Перемещения и электрический потенциал оболочки представляются в виде разложений по нормальной координате [13, 14]

(1)
$\begin{gathered} u(\xi ,\theta ,z) = {{u}_{0}}(\xi ,\theta ) + {{u}_{1}}(\xi ,\theta )z + {{u}_{2}}(\xi ,\theta )\frac{{{{z}^{2}}}}{{2!}} + {{u}_{3}}(\xi ,\theta )\frac{{{{z}^{3}}}}{{3!}}, \hfill \\ {v}(\xi ,\theta ,z) = {{{v}}_{0}}(\xi ,\theta ) + {{{v}}_{1}}(\xi ,\theta )z + {{{v}}_{2}}(\xi ,\theta )\frac{{{{z}^{2}}}}{{2!}} + {{{v}}_{3}}(\xi ,\theta )\frac{{{{z}^{3}}}}{{3!}}, \hfill \\ {\text{ }}w(\xi ,\theta ,z) = {{w}_{0}}(\xi ,\theta ) + {{w}_{1}}(\xi ,\theta )z + {{w}_{2}}(\xi ,\theta )\frac{{{{z}^{2}}}}{{2!}}, \hfill \\ {\text{ }}\varphi (\xi ,\theta ,z) = {{\varphi }_{0}}(\xi ,\theta ) + {{\varphi }_{1}}(\xi ,\theta )z + {{\varphi }_{2}}(\xi ,\theta )\frac{{{{z}^{2}}}}{{2!}}. \hfill \\ \end{gathered} $

Деформации оболочки определяются как

(2)
$\{ \varepsilon \} = {{\{ {{\varepsilon }_{\xi }},{{\varepsilon }_{\theta }},{{\varepsilon }_{{\text{z}}}},{{\gamma }_{{\xi \theta }}},{{\gamma }_{{\xi {\text{z}}}}},{{\gamma }_{{\theta z}}}\} }^{T}},$
где, компоненты деформаций находятся с помощью геометрических соотношений

$\begin{gathered} {{\varepsilon }_{\xi }} = \frac{1}{R}\frac{{\partial u}}{{\partial \xi }},\quad {{\varepsilon }_{\theta }} = \frac{1}{{R + z}}\left( {\frac{{\partial {v}}}{{\partial \theta }} + w} \right),\quad {{\gamma }_{{\xi \theta }}} = \frac{1}{R}\frac{{\partial {v}}}{{\partial \xi }} + \frac{1}{{R + z}}\frac{{\partial u}}{{\partial \theta }}, \\ {{\varepsilon }_{z}} = \frac{{\partial w}}{{\partial z}},\quad {{\gamma }_{{\xi z}}} = \frac{1}{R}\frac{{\partial w}}{{\partial \xi }} + \frac{{\partial u}}{{\partial z}},\quad {{\gamma }_{{\theta z}}} = \frac{1}{{R + z}}\frac{{\partial w}}{{\partial \theta }} + \frac{{\partial {v}}}{{\partial z}} - \frac{{v}}{{R + z}}. \\ \end{gathered} $

Уравнения напряженного состояния оболочки при деформации k-го слоя [15, 16] с учетом сопряженного электрического поля в локальной системе координат O123 (рис. 1) можно записать в виде [14, 17]

(4)
$\begin{gathered} \left\{ {\sigma _{{123}}^{{(k)}}} \right\} = \left[ {{{С}^{{(k)}}}} \right]\left\{ {\varepsilon _{{123}}^{{(k)}}} \right\} - {{\left[ {e_{{123}}^{{(k)}}} \right]}^{T}}\left\{ {E_{{123}}^{{(k)}}} \right\}, \\ \left\{ {D_{{123}}^{{(k)}}} \right\} = \left[ {e_{{123}}^{{(k)}}} \right]\left\{ {\varepsilon _{{123}}^{{(k)}}} \right\} + {{\left[ {\mu _{{123}}^{{(k)}}} \right]}^{T}}\left\{ {E_{{123}}^{{(k)}}} \right\}, \\ \end{gathered} $
где $\sigma _{{123}}^{{(k)}} = \left\{ {\sigma _{{11}}^{{(k)}},\sigma _{{22}}^{{(k)}},\sigma _{{33}}^{{(k)}},\sigma _{{12}}^{{(k)}},\sigma _{{23}}^{{(k)}},\sigma _{{31}}^{{(k)}}} \right\}$ – вектор напряжения k-го слоя оболочки, $\varepsilon _{{123}}^{{(k)}}$ = $\left\{ {\varepsilon _{{11}}^{{(k)}}} \right.$, $\varepsilon _{{22}}^{{(k)}}$, $\varepsilon _{{33}}^{{(k)}}$, $\gamma _{{12}}^{{(k)}}$, $\gamma _{{23}}^{{(k)}}$, $\left. {\gamma _{{31}}^{{(k)}}} \right\}$ – вектор деформации k-го слоя, определяемый по формуле $\left\{ {\varepsilon _{{123}}^{{(k)}}} \right\}$ = $\{ \varepsilon \} \left\{ {\sigma _{{123}}^{{(k)}}} \right\}$, ${{C}^{{(k)}}} = С_{{ij}}^{{(k)}}$, ($i = \overline {1,\;6} $, ${\text{ }}j = \overline {1,\;6} $) – симметричная матрица жесткости k-го слоя, $D_{{123}}^{{(k)}}$ = $\left\{ {D_{{11}}^{{(k)}},D_{{22}}^{{(k)}},D_{{33}}^{{(k)}}} \right\}$ – вектор электрической индукции, $E_{{123}}^{{(k)}}$ = = $\left\{ {E_{{11}}^{{(k)}},E_{{22}}^{{(k)}},E_{{33}}^{{(k)}}} \right\}$ – вектор напряженности электрического поля k-го слоя, $e_{{123}}^{{(k)}} = e_{{ij}}^{{(k)}}$ ($i = \overline {1,\;3} $, $j = \overline {1,\;6} $) – матрица пьезоэлектрических постоянных k-го слоя, $\mu _{{123}}^{{(k)}} = \mu _{{ij}}^{{(k)}}$ ($i = \overline {1,\;3} $, $j = \overline {1,\;3} $) – симметричная матрица диэлектрических проницаемостей при нулевой деформации k-го слоя оболочек.

Электромеханическая связь k-го слоя в общей системе координат $O\xi \theta z$ определяется следующей формулой

(5)
$\begin{gathered} \left\{ {\sigma _{{\xi \theta z}}^{{(k)}}} \right\} = {{\left[ {T_{2}^{{(k)}}} \right]}^{T}}\left[ {{{С}^{{(k)}}}} \right]\left[ {T_{2}^{{(k)}}} \right]\left\{ \varepsilon \right\} - {{\left[ {e_{{\xi \theta z}}^{{(k)}}} \right]}^{T}}\left\{ {E_{{\xi \theta z}}^{{(k)}}} \right\}, \hfill \\ {\text{ }}\left\{ {D_{{\xi \theta z}}^{{(k)}}} \right\} = \left[ {e_{{\xi \theta z}}^{{(k)}}} \right]\left\{ \varepsilon \right\} + {{\left[ {\mu _{{\xi \theta z}}^{{(k)}}} \right]}^{T}}\left\{ {E_{{\xi \theta z}}^{{(k)}}} \right\}. \hfill \\ \end{gathered} $

Здесь $\left[ {T_{2}^{{(k)}}} \right]$ – матрица перехода [18], принимаемая в виде

(6)
$\left[ {T_{2}^{{\left( k \right)}}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\cos }}^{2}}{{\beta }^{{\left( k \right)}}}}&{{{{\sin }}^{2}}{{\beta }^{{\left( k \right)}}}}&0&0&0&{\sin {{\beta }^{{\left( k \right)}}}\cos {{\beta }^{{\left( k \right)}}}} \\ {{{{\sin }}^{2}}{{\beta }^{{\left( k \right)}}}}&{{{{\cos }}^{2}}{{\beta }^{{\left( k \right)}}}}&0&0&0&{ - \sin {{\beta }^{{\left( k \right)}}}\cos {{\beta }^{{\left( k \right)}}}} \\ 0&0&1&0&0&0 \\ 0&0&0&{\cos {{\beta }^{{\left( k \right)}}}}&{ - \sin {{\beta }^{{\left( k \right)}}}}&0 \\ 0&0&0&{\sin {{\beta }^{{\left( k \right)}}}}&{\cos {{\beta }^{{\left( k \right)}}}}&0 \\ { - \sin 2{{\beta }^{{\left( k \right)}}}}&{\sin 2{{\beta }^{{\left( k \right)}}}}&0&0&0&{{{{\cos }}^{2}}{{\beta }^{{\left( k \right)}}} - {{{\sin }}^{2}}{{\beta }^{{\left( k \right)}}}} \end{array}} \right]$
и $\left\{ {\sigma _{{\xi \theta z}}^{{(k)}}} \right\} = {{\left\{ {\sigma _{\xi }^{{(k)}},\sigma _{\theta }^{{(k)}},\sigma _{z}^{{(k)}},\sigma _{{\xi \theta }}^{{(k)}},\sigma _{{\xi z}}^{{(k)}},\sigma _{{\theta z}}^{{(k)}}} \right\}}^{T}}$, $D_{{\xi \theta z}}^{{(k)}} = \left\{ {D_{\xi }^{{(k)}},D_{\theta }^{{(k)}},D_{z}^{{(k)}}} \right\}$ = $D_{{123}}^{{(k)}}$, $e_{{\xi \theta z}}^{{(k)}} = e_{{123}}^{{(k)}}$, $\mu _{{\xi \theta z}}^{{(k)}} = \mu _{{123}}^{{(k)}}$, $E_{{\xi \theta z}}^{{(k)}}$ = $\left\{ {E_{\xi }^{{(k)}},E_{\theta }^{{(k)}},E_{z}^{{(k)}}} \right\}$ = $E_{{123}}^{{(k)}}$ – электроупругостные параметры k-го слоя оболочки в общей системе координат $O\xi \theta z$.

Уравнения Максвелла для электрического поля в материальных средах, пренебрегая в них магнитными эффектами, можно привести к уравнениям электростатики. Отсюда следует, что вектор напряженности можно выразить [15, 19] через потенциал $\varphi $

(7)
$E_{\xi }^{{(k)}} = - \frac{{\partial \varphi }}{{{{A}_{1}}\partial \xi }},\quad E_{\theta }^{{(k)}} = - \frac{{\partial \varphi }}{{{{A}_{2}}\partial \theta }},\quad E_{z}^{{(k)}} = - \frac{{\partial \varphi }}{{\partial z}},$
где ${{A}_{1}} = R$, ${{A}_{2}} = 1 + z{\text{/}}R$ – параметры Ламе цилиндрической оболочки.

Обозначая электрический потенциал, действующий на верхнюю и нижнюю поверхности оболочки через ${{\varphi }^{ + }}$ и ${{\varphi }^{ - }}$, соответственно, из четвертого равенства системы (1) получим

(8)
${{\varphi }_{1}} = \frac{{{{\varphi }^{ + }} - {{\varphi }^{ - }}}}{{2h}},\quad {{\varphi }_{2}} = - \frac{{{{\varphi }_{0}}}}{{{{h}^{2}}}} + \frac{{{{\varphi }^{ + }} + {{\varphi }^{ - }}}}{{2{{h}^{2}}}}.$

Для построения основных уравнений теории цилиндрических оболочек с учетом пьезоэлектрического эффекта используется вариационный принцип Лагранжа [20]

(9)
$\delta U - \delta A = 0.$

В уравнении (9) вариация потенциальной энергии $\delta U$, состоящая из энергий механической деформации и электрического поля, определяется как

(10)
$\delta U = \sum {\int {(\sigma \delta \varepsilon + } D\delta E)dV} .$

Работа внешних нагрузок представляется суммой работ механических нагрузок и электрических зарядов Q на поверхностях оболочки, в результате вариация $\delta A$ находится по формуле

(11)
$\delta A = \sum {\int {{{q}_{{i3}}}(\delta {{u}_{i}} + \delta {{{v}}_{i}} + \delta {{w}_{i}})} } dS + \sum {\int {Q\delta \varphi dS} } .$

Подставляя выражения (10) и (11) в равенство (9), получим систему уравнений равновесия теории композиционных цилиндрических оболочек в перемещениях и потенциалах с учетом пьезоэлектрического эффекта

$\frac{{\partial N_{{11}}^{{\left( 0 \right)}}}}{{\partial \xi }} + \frac{{\partial N_{{21}}^{{\left( 0 \right)}}}}{{\partial \theta }} = 0,$
$\frac{{\partial N_{{11}}^{{\left( i \right)}}}}{{\partial \xi }} + \frac{{\partial N_{{21}}^{{\left( i \right)}}}}{{\partial \theta }} - RN_{{13}}^{{\left( {i - 1} \right)}} = 0,\quad (i = \overline {1,\;3} ),$
$\frac{{\partial N_{{12}}^{{\left( 0 \right)}}}}{{\partial \xi }} + \frac{{\partial N_{{22}}^{{\left( 0 \right)}}}}{{\partial \theta }} + N_{{23}}^{{\left( 0 \right)}} = 0,$
(12)
$\frac{{\partial N_{{12}}^{{\left( i \right)}}}}{{\partial \xi }} + \frac{{\partial N_{{22}}^{{\left( i \right)}}}}{{\partial \theta }} + N_{{23}}^{{\left( i \right)}} - RN_{{23}}^{{\left( {i - 1} \right)}} - iN_{{23}}^{{\left( i \right)}} = 0,\quad (i = \overline {1,\;3} ),$
$\frac{{\partial N_{{13}}^{{\left( 0 \right)}}}}{{\partial \xi }} + \frac{{\partial N_{{23}}^{{\left( 0 \right)}}}}{{\partial \theta }} - N_{{22}}^{{\left( 0 \right)}} + Rp_{z}^{{\left( 0 \right)}} = 0,$
$\frac{{\partial N_{{13}}^{{\left( j \right)}}}}{{\partial \xi }} + \frac{{\partial N_{{23}}^{{\left( j \right)}}}}{{\partial \theta }} - N_{{22}}^{{\left( j \right)}} - RN_{{33}}^{{\left( {j - 1} \right)}} + Rp_{z}^{{\left( j \right)}} = 0,\quad (j = \overline {1,\;2} ),$
$\frac{{\partial ({{h}^{2}}ND_{1}^{{(0)}} - ND_{1}^{{(2)}})}}{{\partial \xi }} + \frac{{\partial ({{h}^{2}}ND_{2}^{{(0)}} - ND_{2}^{{(2)}})}}{{\partial \theta }} - 2ND_{3}^{{(1)}} = 0.$

Воспользовавшись стандартными краевыми условиями трехмерной теории электроупругости [8], получим соответствующие краевые условия при стандартном закреплении краев оболочки:

1) на жестко защемленном краю: ${{u}_{i}} = {{{v}}_{i}} = {{w}_{i}} = 0$, ${{\varphi }_{0}} = {\text{0}}$, ($i = \overline {1,\;3} $);

2) на шарнирно защемленном краю: $N_{{11}}^{{(j)}} = 0$, ($j = \overline {0,\;3} $), ${{{v}}_{i}} = {{w}_{i}} = 0$ ${{\varphi }_{0}} = {\text{0}}$, ($i = \overline {1,\;3} $);

3) на свободном краю: $N_{{11}}^{{(i)}} = N_{{12}}^{{(i)}} = N_{{13}}^{{(i)}} = 0$, ${{\varphi }_{0}} = {\text{0}}$, ($i = \overline {0,\;3} $).

Здесь $N_{{ij}}^{{\left( k \right)}}$ ($i = \overline {1,\;3} $, $j = \overline {1,\;3} $, $k = \overline {0,\;3} $) – механические усилия и моменты, $ND_{i}^{{\left( k \right)}}$ ($i = \overline {1,\;3} $, $k = \overline {0,\;2} $) – электрические усилия и моменты, для которых приняты следующие обозначения:

$\left( {N_{{11}}^{{\left( i \right)}},N_{{12}}^{{\left( i \right)}},N_{{13}}^{{\left( i \right)}}} \right) = \sum\limits_{k = 1}^{n + 2} {\int\limits_{ - h}^h {\left( {{{\sigma }_{\xi }},{{\sigma }_{{\xi \theta }}},{{\sigma }_{{\xi z}}}} \right)\frac{{{{z}^{i}}}}{{i!}}dz} } ,\quad \left( {i = \overline {0,\;3} } \right),$
$\left( {N_{{22}}^{{\left( i \right)}},N_{{21}}^{{\left( i \right)}},N_{{23}}^{{\left( i \right)}}} \right) = \sum\limits_{k = 1}^{n + 2} {\int\limits_{ - h}^h {\left( {{{\sigma }_{\theta }},{{\sigma }_{{\xi \theta }}},{{\sigma }_{{\theta z}}}} \right)\frac{{{{z}^{i}}}}{{i!}}dz} } ,\quad \left( {i = \overline {0,\;3} } \right),$
(13)
$\begin{gathered} N_{{33}}^{{\left( j \right)}} = \sum\limits_{k = 1}^{n + 2} {\int\limits_{ - h}^h {{{\sigma }_{z}}\frac{{{{z}^{j}}}}{{j!}}dz} } ,\quad \left( {j = \overline {0,\;2} } \right), \\ ND_{1}^{{\left( i \right)}} = \sum\limits_{k = 1}^{n + 2} {\int\limits_{ - h}^h {{{D}_{1}}} \left( {1 + \frac{z}{R}} \right)\frac{{{{z}^{i}}}}{{i!}}dz} ,\quad ND_{2}^{{\left( i \right)}} = \sum\limits_{k = 1}^{n + 2} {\int\limits_{ - h}^h {{{D}_{2}}} \frac{{{{z}^{i}}}}{{i!}}dz} ,\quad \left( {i = \overline {0,2} } \right), \\ \end{gathered} $
$ND_{3}^{{\left( i \right)}} = \sum\limits_{k = 1}^{n + 2} {\int\limits_{ - h}^h {{{D}_{3}}} \left( {1 + \frac{z}{R}} \right)\frac{{{{z}^{i}}}}{{i!}}dz} ,\quad (i = \overline {0,\;2} ),$
$p_{z}^{{(i)}} = q_{{33}}^{ + }(\xi ,\theta )\left( {1 + \frac{h}{R}} \right)\left( {\frac{{{{h}^{i}}}}{{i!}}} \right) - q_{{33}}^{ - }(\xi ,\theta )\left( {1 - \frac{h}{R}} \right)\left( {\frac{{{{{( - h)}}^{i}}}}{{i!}}} \right),\quad \left( {i = \overline {0,\;3} } \right).{\text{ }}$

Решение краевой задачи. Рассматривается замкнутая круговая композиционная цилиндрическая оболочка, края которой жестко защемлены. Для приведения краевой задачи (12)–(13) к системе обыкновенных дифференциальных уравнений используются разложения перемещений и электрических потенциалов в тригонометрические ряды по окружной координате $\theta $ вида

$q\left( {\xi ,\theta } \right) = \sum\limits_{m = 1}^\infty {{{Q}_{m}}\left( \xi \right)\cos (m\theta } ) + {{Q}_{0}}\left( \xi \right),$
${{u}_{i}}\left( {\xi ,\theta } \right) = \sum\limits_{m = 1}^\infty {{{U}_{i}}\left( \xi \right)\cos (m\theta )} + {{U}_{{i0}}}\left( \xi \right),\quad i = \overline {0,\;3} ,$
(14)
${{v}_{i}}\left( {\xi ,\theta } \right) = \sum\limits_{m = 1}^\infty {{{V}_{k}}\left( \xi \right)\sin (m\theta )} + {{V}_{{i0}}}\left( \xi \right),\quad i = \overline {0,\;3} ,$
${{w}_{j}}\left( {\xi ,\theta } \right) = \sum\limits_{m = 1}^\infty {{{W}_{j}}\left( \xi \right)\cos m\theta } + {{W}_{{j0}}}\left( \xi \right),\quad j = \overline {0,\;2} ,$
$\varphi \left( {\xi ,\theta } \right) = \sum\limits_{m = 1}^\infty {{{\varphi }_{m}}\left( \xi \right)\cos (m\theta } ) + {{\varphi }_{0}}\left( \xi \right).$

После подстановки разложений (14) в уравнения (12) и краевые условия ${{u}_{i}} = {{{v}}_{i}} = {{w}_{i}} = 0$, ${{\varphi }_{0}} = {\text{0}}$, ($i = \overline {1,\;3} $), находим систему обыкновенных дифференциальных уравнений для функций ${{u}_{{im}}}$, ${{{v}}_{{im}}}$, ${{w}_{{lm}}}$, ${{\varphi }_{{lm}}}$, $i = \overline {0,\;3} $, $l = \overline {0,\;2} $, $m = 1,\;2,\;3 \ldots $, которые здесь не приводятся по причине их громоздкости.

Пример расчета. В качестве примера рассматривается замкнутая цилиндрическая композиционная оболочка из smart-материала PZT-4 радиусом $R = 0.25$ м, длиной $L = 4R$, относительной толщиной $2h{\text{/}}R$ = 1/50. Электроупругостные характеристики материала: модули Юнга Y1 = Y2 = 81.3 (GPa) и Y3 = 64.5 (GPa), коэффициенты Пуасона ${{{v}}_{{12}}} = 0.329$ и ${{{v}}_{{13}}} = {{{v}}_{{23}}} = 0.432$, модули сдвига ${{G}_{{12}}} = 30.6$ (GPa) и ${{G}_{{13}}} = {{G}_{{23}}} = 25.6$ (GPa), пьезоэлектрические константы: ${{e}_{{31}}} = {{e}_{{32}}} = - 5.20$ (Cm–1), ${{e}_{{33}}} = {\text{15}}{\text{.08}}$ (Cm–2) и ${{e}_{{15}}} = {{e}_{{24}}} = 0$, диэлектрические проницаемости: ${{\mu }_{{11}}} = 5.62$ (10–9 Fm–1) и ${{\mu }_{{22}}} = {{\mu }_{{33}}}$ = = 6.46 (10–9 Fm–1). Оболочка состоит из шести слоев и находится под действием нагрузок в двух вариантах: 1) механическая нагрузка $q_{{33}}^{ + }(\xi ,\theta )$ = ${{Q}_{0}}(\xi )\cos (2\theta )$, 2) электрический потенциал ${{\varphi }^{ + }}(\xi ,\theta )$ = ${{V}_{0}}(\xi )\cos (2\theta )$.

Результаты вычисления нормальных напряжений на жестко защемленном краю оболочки, имеющей симметричное и антисимметричное распределения слоев показаны на рис. 2, 3.

Рис. 2.

Распределение напряжений по толщине на краю в первом варианте: (а) – при симметричном распределении слоев [0/90°/0/0/90°/0]; (б) – при антисимметричном распределении слоев [0/90°/–90°/90°/–90°/0].

Рис. 3.

Распределение напряжений по толщине на краю во втором варианте: (а) – при симметричном распределении слоев [0/90°/–90°/–90°/90°/0]; (б) – при антисимметричном распределении слоев [0/45°/–45°/45°/–45°/0].

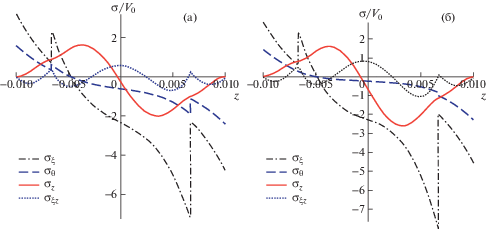
Анализ полученных результатов распределения напряжений по толщине оболочки показывает, что в первом варианте на жестко защемленном краю поперечные нормальные и касательные напряжения ${{\sigma }_{z}}$, ${{\sigma }_{{\xi z}}}$ составляют примерно 60 и 28% от максимальных нормальных напряжений при симметричном распределении слоев [0/90°/0/0/90°/0], а при антисимметричном распределении слоев [0/90°/–90°/90°/–90°/0] – 65 и 30%, соответственно.

Аналогично, во втором варианте на жестко защемленном краю поперечные нормальные и касательные напряжения ${{\sigma }_{z}}$, ${{\sigma }_{{\xi z}}}$ составляют примерно 28 и 8% от максимальных нормальных напряжений при симметричном распределении слоев [0/90°/–90°/–90°/90°/0], а при антисимметричном распределении слоев [0/45°/–45°/45°/–45°/0] –32 и 12%, соответственно.

Расчеты напряженного состояния в зонах, удаленных от краев оболочки, показали, что поперечные нормальные напряжения, как и следовало ожидать, малы по сравнению с остальными напряжениями, что позволяет ими пренебречь.

Заключение. На основании уточненной теории построена математическая модель электромеханического состояния композиционных цилиндрических оболочек под действием произвольных нагрузкок с учетом пьезоэлектрического эффекта.

Приведены примеры расчетов напряженного состояния замкнутой цилиндрической композиционной оболочки под действием механических и электрических нагрузок с симметричным и ассиметричным распределениями слоев. Установлено, что в зонах жесткого закрепления имеют место дополнительные поперечные нормальные и касательные напряжения типа “погранслой”, которые необходимо учитывать при расчете прочности и долговечности непрерывных соединений элементов конструкций.

Список литературы

  1. Baker A., Dutton St., Kelly D. Composite materials for aircraft structures. Publisher: AIAA Inc, 2004. 603 p.

  2. Гришанина Т.В., Шклярчук Ф.Н. Динамика управляемых конструкций. М.: Изд-во МАИ, 2007. 326 с.

  3. Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука, 1976. 512 с.

  4. Friedrlchs K.O. Kirchoff′s boundary conditions and the edge effect for elastic plates // Proc. Sympos. Appl. Math. 1950. V. 3. P. 258.

  5. Timoshenko S.P., Voinovsky-Krieger S. Theory of plates and shells. McGrawHill, 1959. 591 p.

  6. Фирсанов В.В., Чан. Н.Д. Энергетически согласованная теория цилиндрических оболочек // Проблемы машиностроения и надежности машин. 2011. № 6. С. 49.

  7. Фирсанов В.В., Фам В.Т. Напряженно-деформированное состояние сферической оболочки под действием произвольной нагрузки на основе неклассической теории // Проблемы прочности и пластичности. 2019. Т. 81. № 3. С. 64.

  8. Firsanov V.V., Doan T.N. Investigation of the statics and free vibrations of cylindrical shells on the basis of a nonclassical theory // Composites: Mechanics. 2015. V. 6. Iss. 2. P. 135.

  9. Reddy J.N. Mechanics of laminated composite plates and shells: theory and analysis. CRC Press, 2004. 831 p.

  10. Гольденвейзер А.Л. Построение приближенной теории оболочек при помощи асимптотического интегрирования уравнений теории упругости // Прикладная математика и механика. 1963. Т. 27. № 4. С. 593.

  11. Зверяев Е.М., Олехова Л.В. Итерационная трактовка полуобратного метода Сен-Венана при построении уравнений тонкостенных элементов конструкций из композиционного материала // Труды МАИ. 2015. № 79. С. 27.

  12. Улитко А.Ф. Метод собственных векторных функций в пространственных задачах теории упругости. Киев: Наукова думка, 1979. 262 с.

  13. Васильев В.В., Лурье С.А. К проблеме уточнения теории пологих оболочек // Известия АН СССР. Механика твердого тела. 1990. № 6. С. 139.

  14. Xiao-Hong Wu, Chongqing Chen, Ya-Peng Shen, Xiao-Geng Tian. A high order theory for functionally graded piezoelectric shells // International Journal of Solids and Structures. 2002. № 39 (20). P. 5325.

  15. Партон В.З., Кудрявцев Б.А. Электромагнитоупругость пьезоэлектрических и электропроводных тел. M.: Наука, 1998. 470 с.

  16. Tzou H.S. Piezoelectric Shells, Distributed Sensing and Control of Continua. 1993. ISBN 978-94-010-4784-5.

  17. Димитриенко Ю.И., Морозов А.Н., Соколов А.П., Ничеговский Е.С. Моделирование эффективных пьезоэлектроупругих композиционных материалов // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2010. № 3. С. 86.

  18. Амбарцумян С.А. Теория анизотропных пластин. М.: Наука, 1967. 68 с.

  19. Гринченко В.Т., Улитко А.Ф., Шульга Н.А. Электроупругость. Киев: Наукова думка, 1989. Т. 5. 280 с.

  20. Власов В.З. Общая теория оболочек. Избранные труды. Общая теория оболочек. М.: АН СССР, 1962. Т. 1. 528 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал