Проблемы машиностроения и надежности машин, 2021, № 4, стр. 26-36
Оценка вероятности усталостного разрушения конструкционных элементов с учетом статистического разброса механических характеристик прочности материала и остаточной дефектности
Ю. Г. Матвиенко 1, Д. А. Кузьмин 2, Д. О. Резников 1, *, В. В. Потапов 2
1 Институт машиноведения им. А.А. Благонравова, РАН
Москва, Россия
2 Всероссийский научно-исследовательский институт по эксплуатации атомных электростанций
Москва, Россия
* E-mail: mibsts@mail.ru
Поступила в редакцию 30.12.2020
После доработки 30.03.2021
Принята к публикации 26.04.2021
Аннотация
В статье представлен метод оценки вероятности разрушения конструктивных элементов технических систем под действием однократных статических и циклических нагрузок, позволяющий учитывать разброс механических свойств материалов и размеров, остаточных макродефектов, невыявленных в ходе неразрушающего контроля. Представленный метод можно использовать при реализации вероятностного и риск-ориентированного подходов к обеспечению прочности, ресурса и безопасности технических систем в реальных условиях эксплуатации и корректировке типовых программ эксплуатации с точки зрения выбора периодичности и объема неразрушающего контроля
1. Постановка задачи. В задачах оценки и обеспечения конструкционной прочности и ресурса конструктивных элементов технических систем в реальных условиях эксплуатации неизбежно присутствует высокий уровень неопределенности, обусловленный вариативностью механических свойств и стохастической природой процессов их деградации, а также разбросом размеров трещин и других макродефектов. Дефекты могут возникнуть при изготовлении, монтаже или в процессе эксплуатации и не быть выявленными средствами неразрушающего контроля, которые не позволяют на современном уровне развития техники обеспечить 100% выявляемость дефектов. Вследствие чего на практике всегда приходится учитывать наличие остаточной дефектности, под которой понимается совокупность дефектов, которая остается в оборудовании после неразрушающего контроля и ремонта выявленных дефектов [1–4]. Отдельная группа неопределенностей связана с вариативностью режимов эксплуатационных нагружений, а также возможностью реализации расчетных и нерасчетных экстремальных воздействий на рассматриваемые конструктивные элементы.
Конструкционная прочность и эксплуатационный ресурс рассматриваемых конструктивных элементов считаются обеспеченными, если для всей совокупности доминирующих механизмов достижения предельных состояний i = 1, 2, …, k на протяжении всего срока эксплуатации элемента ${{T}_{{\text{Э}}}}$ выполняются условия [5–12]
(1)
$\Sigma _{i}^{C}(t){\text{/}}\Sigma _{i}^{{\text{Э}}}(t) > 1,\quad i = {\text{1,}}\;{\text{2,}}\;...{\text{,}}\;k\quad \forall t \in [0;{{T}_{{\text{э}}}}],$Традиционно при решении задач прочности раскрытие указанных неопределенностей осуществлялось в рамках детерминистического подхода путем введения системы запасов прочности n1, n2, …, nk по основным механизмам достижения предельных состояний, при которых неопределенные параметры $\Sigma _{i}^{C}(t)$, $\Sigma _{i}^{{\text{Э}}}(t)$ (i = 1, 2, …, k) в системе неравенств (1) заменяются на их детерминированные характеристики, например, математические ожидания E{$\Sigma _{i}^{C}(t)$}, E{$\Sigma _{i}^{{\text{Э}}}(t)$}, а для компенсации возможных отклонений от указанных математических ожиданий (в том числе, минимизации влияния неучтенных нагрузок), вместо числа 1 в правые части неравенств (1) вводятся соответствующие величины запасов n1 > 1, n2 > 1, …, nk > 1
С развитием вероятностного и далее риск-ориентированного подходов, обусловленных необходимостью решения проблем по минимизации затрат жизненного цикла, встает задача оценки вероятности разрушения конструктивных элементов под действием рассматриваемых режимов нагружения (PF1, PF2, …, PFk) [12] и сопоставления полученных оценок с некоторыми нормативными предельно-допустимыми значениями вероятности разрушения [PF], которая в зависимости от ответственности рассматриваемой конструкции выбирается в диапазоне 10–5–10–8, год–1 [9, 13]. При этом конструкционная прочность и эксплуатационный ресурс рассматриваемого конструктивного элемента по основным механизмам достижения предельных состояний считаются обеспеченными, если выполняется система неравенств
Решение поставленной задачи в вероятностной постановке предполагает описание неопределенностей с помощью вероятностных распределений неопределенных параметров и получение расчетных оценок вероятности разрушения аналитическим или численным способом. Отдельной задачей является обоснованный выбор значений нормативных, предельно-допустимых значений вероятности разрушения [PFi(t)] по рассматриваемым механизмам достижения предельных состояний, который осуществляется с учетом критичности элемента и последствий, наступающих в случае его разрушения.
2. Оценка вероятности разрушения элемента при однократном статическом нагружении. Используя записанную в интегральной форме теорему о полной вероятности, уравнение для оценки вероятности разрушения компонента, находящегося в хрупком состоянии и содержащего трещиноподобный дефект, можно записать в виде [1, 2]
Коэффициент интенсивности напряжений в зоне поверхностной трещины определяют по уравнению ${{K}_{I}} = {{f}_{k}}\sigma \sqrt {\pi a} $, где fk – корректирующая функция на геометрию и размер трещины, ее место расположения и схему нагружения.
Если ввести допущение о детерминированности приложенных напряжений (σ), то вероятность разрушения будет определяться более простым выражением
(2)
${{P}_{F}} = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {{{f}_{{KIc}}}({{K}_{{Ic}}})P(a \geqslant {{a}_{с}})d{{K}_{{Ic}}}} = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {{{f}_{{KIc}}}({{K}_{{Ic}}})\left( {1 - F({{a}_{c}})} \right)d{{K}_{{Ic}}}} .$Выражение (2) представляет собой запись теоремы о полной вероятности: вероятность разрушения представляет собой сложное событие a > aC(KIc)|KIc ∈ dKIc, объединяющее два связанных события: 1) событие 1 – вязкость разрушения KIc оказывается в интервале dKIc (KIc ∈ dKIc). Вероятность этого события равняется fKIc(KIc)dKIc; 2) событие 2 – размер дефекта a превышает критическую величину aC (a > aC). Вероятность этого события, соответственно, P(a > aC).
Пределы интегрирования в выражении (2) можно выбрать из условия
Пусть величина вязкости разрушения распределена по нормальному закону
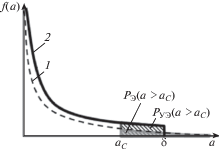
Будем считать, что случайная величина “характерный размер дефекта” распределена согласно экспоненциальному закону [1] (рис. 1, кривая 1)
где E{a} – математическое ожидание случайной величины a.Рис. 1.
Распределение величины “размер дефекта” a: 1 – экспоненциальное распределение (Э); 2 – усеченное экспоненциальное распределение (УЭ).
Тогда второй множитель подынтегрального выражения в уравнении (2) можно записать в виде
При этом уравнение (2) можно переписать как
Учитывая, что
получим выражение для вероятности разрушения конструктивного элемента с трещиной(6)
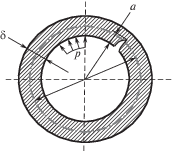
${{P}_{F}} = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {\frac{1}{{\sqrt {2\pi } S\{ {{K}_{{Ic}}}\} }}{{e}^{{ - \frac{{{{{({{K}_{{Ic}}} - E\{ {{K}_{{Ic}}}\} )}}^{2}}}}{{2S{{{\{ {{K}_{{Ic}}}\} }}^{2}}}}}}}{{e}^{{ - \frac{1}{{E\{ a\} }}{{{\left( {\frac{{{{K}_{{Ic}}}}}{{{{f}_{k}}\sigma \sqrt \pi }}} \right)}}^{2}}}}}d{{K}_{{Ic}}}} .$Рассмотрим численный пример расчета вероятности разрушения элемента трубопровода, нагруженного внутренним давлением, содержащего осевую поверхностную трещину на внутренней стенке (рис. 2). Исходные данные задачи приведены в табл. 1.
Таблица 1.
Численные значения параметров
| Внутреннее давление в трубопроводе, p0 (МПа) | 8 |
| Диаметр, D (м) | 1.26 |
| Толщина стенки, δ (м) | 0.025 |
| Окружное напряжение, σ (МПА) | 201.6 |
| Вязкость разрушения, KIc | |
| Математическое ожидание, E{KIc} (МПа $\sqrt {\text{м}} $) | 61 |
| Коэффициент вариации, νKIc | 0.1 |
В рассматриваемом примере для консервативной оценки допускается в качестве характерного размера трещины a принимать ее глубину, т.е. рассматривать протяженный дефект длиной, превышающей на порядок ее глубину. Значение корректирующей функции fk для протяженного дефекта в выражении для коэффициента интенсивности напряжения принимается равным 1.12 [15].
Будем считать, что после проведения неразрушающего контроля осуществляется идентификация и ремонт выявленных дефектов. При этом размер невыявленных дефектов, определяемый качеством (объемом и глубиной) проведения неразрушающего контроля, является вероятностной величиной, распределенной по экспоненциальному закону. В рассматриваемом примере ее математическое ожидание принимается равным E{a} = 2.00 × 10–3. Иными словами, при проведении расчета постулируется наличие дефекта типа трещины, глубина которой точно неизвестна и считается вероятностной величиной, распределенной по экспоненциальному закону с математическим ожиданием E{a} = 2.00 × 10–3 м.
Согласно соотношению (6) для рассматриваемого примера вероятность разрушения элемента при однократном статическом нагружении составляет PF = 6.51 × 10–5.
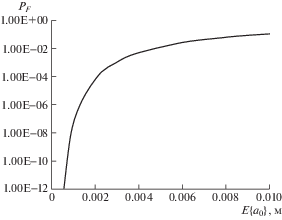
Зависимость вероятности разрушения от величины математического ожидания размера трещины E{a} представлена на рис. 3.
Рис. 3.
Зависимость вероятности хрупкого разрушения при однократном статическом нагружении от математического ожидания глубины трещины.
Если вместо экспоненциального по выражению (4) в качестве распределения глубины трещины a использовать усеченное экспоненциальное распределение вида
(7)
$F(a) = \frac{1}{{1 - {{e}^{{ - \frac{1}{{E\{ a\} }}\delta }}}}} - \frac{{{{e}^{{ - \frac{1}{{E\{ a\} }}a}}}}}{{1 - {{e}^{{ - \frac{1}{{E\{ a\} }}\delta }}}}},$Таким образом, в случае использования в рассмотренном численном примере усеченного экспоненциального распределения вероятность разрушения составит PF = = 6.14 × 10–5. При этом различие оценок вероятности разрушения при использовании экспоненциального и усеченного экспоненциального распределений составляет порядка 6%.
3. Оценка вероятности усталостного разрушения с учетом разброса начальных размеров трещины a0 и вязкости разрушения KIc. Рассмотрим задачу циклического нагружения конструктивного элемента с трещиноподобным дефектом. Используя (2), можно записать выражение для оценки вероятности разрушения после N циклов нагружения с учетом подрастания трещины от исходной глубины a0 до текущей глубины aN
(8)
${{P}_{{{{F}_{N}}}}} = {{P}_{F}}({{\tau }_{N}}) = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {{{f}_{{{{K}_{{Ic}}}}}}({{K}_{{Ic}}})P({{a}_{N}} > {{a}_{C}})d{{K}_{{Ic}}}} .$Будем считать, что кинетика трещины описывается модифицированным уравнением Пэриса
где С и m – постоянные, зависящие от материала и условий нагружения; R – коэффициент асимметрии цикла нагружения; ΔK – размах коэффициента интенсивности напряжений в цикле нагружения. Будем считать, что начальный размер трещины a0 является случайной величиной, распределенной по экспоненциальному закону (3).При этом глубина трещины после N циклов нагружения будет являться функцией случайной величины “начальная глубина трещины” a0, т.е. между случайными величинами aN и a0 будет существовать детерминированная функциональная зависимость. Разделяя переменные и интегрируя левую и правую части выражения (9) можно получить
(10)
$N = \frac{{a_{N}^{{1 - \frac{m}{2}}} - a_{0}^{{1 - \frac{m}{2}}}}}{{C\left( {1 - \frac{m}{2}} \right){{{\left( {\frac{{{{f}_{k}}\sqrt \pi }}{{(1 - R)}}\Delta \sigma } \right)}}^{m}}}},$Из уравнения (10) можно записать выражение для глубины трещины после N циклов нагружения
(11)
${{a}_{N}} = {{\left( {{{a}_{0}}^{{1 - \frac{m}{2}}} + NC\left( {1 - \frac{m}{2}} \right){{{\left( {\frac{{{{f}_{k}}\sqrt \pi }}{{1 - R}}\Delta \sigma } \right)}}^{m}}} \right)}^{{\frac{2}{{2 - m}}}}}.$Условие разрушения после N циклов нагружения имеет вид
Таким образом, в рассматриваемой постановке величина aN по выражению (11) будет являться функцией только случайной величины a0.
Введем понятие критической начальной глубины трещины ${{a}_{{0{{C}_{N}}}}}$ (рис. 4), под которой будем понимать такую начальную глубину трещины, которая после N циклов нагружения при заданном уровне размаха номинальных напряжений в цикле нагружения Δσ достигнет критического размера aC, определяемого с учетом соотношения (5) и возможности изменения параметров цикла нагружения в виде
В связи с тем, что в рассматриваемой постановке кинетика роста трещины является детерминированной и между величинами a0 и aN существует детерминированная функциональная зависимость, условие разрушения в момент времени τN, соответствующий N циклам нагружения, можно выразить через соотношение между начальной глубиной трещины a0 и величиной ${{a}_{{0{{C}_{N}}}}}$
Величину ${{a}_{{0{{C}_{N}}}}}$ можно получить, выразив a0 из (10)
(13)
${{a}_{{0{{С}_{N}}}}} = {{\left( {a_{С}^{{(2 - m)/2}} - NC\left( {1 - \frac{m}{2}} \right){{{\left( {\frac{{{{f}_{k}}}}{{1 - R}}\Delta \sigma \sqrt \pi } \right)}}^{m}}} \right)}^{{2/(2 - m)}}}.$Учитывая (12), выражение для вероятности усталостного разрушения после N циклов нагружения (8) можно переписать в виде
(14)
${{P}_{F}}({{\tau }_{N}}) = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {{{f}_{{{{K}_{{Ic}}}}}}({{K}_{{Ic}}})P({{a}_{0}} > {{a}_{{0{{C}_{N}}}}})d{{K}_{{Ic}}}} .$Второй множитель подынтегрального выражения в уравнении (14) можно представить через функцию распределения F(a0) случайной величины “начальная глубина трещины”
Или с учетом (3) для экспоненциального распределения начальной глубины трещины a0
Тогда с учетом выражений (5) и (13)
При этом выражение для оценки вероятности разрушения после N циклов нагружения можно записать в виде
(15)
${{P}_{F}}({{\tau }_{N}}) = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {\frac{1}{{\sqrt {2\pi } S\{ {{K}_{{Ic}}}\} }}{\kern 1pt} {\kern 1pt} } {{e}^{{ - \,\frac{{{{{({{K}_{{Ic}}} - E\{ {{K}_{{Ic}}}\} )}}^{2}}}}{{2S{{{\{ {{K}_{{Ic}}}\} }}^{2}}}}}}}{{e}^{{ - \,\frac{{{{{\left( {{{{\left( {\frac{{{{K}_{{IC}}}(1 - R)}}{{{{f}_{k}}\Delta \sigma \sqrt \pi }}} \right)}}^{{2 - m}}} - NC\left( {1 - \frac{m}{2}} \right){{{\left( {\frac{{{{f}_{k}}}}{{1 - R}}\Delta \sigma \sqrt \pi } \right)}}^{m}}} \right)}}^{{2/(2 - m)}}}}}{{E\{ {{a}_{0}}\} }}}}}d{{K}_{{Ic}}}.$Следовательно, вероятность усталостного разрушения (15) зависит от: 1) числа циклов нагружения N в интервале времени между проведением оценки состояния элемента методами неразрушающего контроля (N = ντ, ν – годовая частота циклов, τ – интервал времени между проведением оценок состояния, год); 2) качества проведения неразрушающего контроля, которое определяет параметры распределения остаточной дефектности, которая не была выявлена в ходе неразрушающего контроля и, следовательно, была пропущена в эксплуатацию, E{a0}; 3) размаха действующих напряжений Δσ; 4) параметров распределения величины вязкости разрушения KIC. Первые два из перечисленных факторов позволяют сформировать программу эксплуатации рассматриваемого элемента с точки зрения периодичности и объема контроля, позволяющую обеспечить его конструкционную прочность, надежность, ресурс, безопасность при заданных режимах нагружения и свойствах конструкционного материала.
В качестве примера использования полученной расчетной зависимости обратимся к рассмотренному в п. 2 элементу трубопровода, который в данном случае будет подвергаться циклическому нагружению внутренним давлением со средним значением в цикле p0 = 7.6 МПа, размахом за цикл нагружения Δp = 0.8 МПа, коэффициентом асимметрии цикла R = 0.9 и частотой нагружения ν = 500 год–1. Константы уравнения Пэриса принимаются равными: C = 3.00 × 10–11, m = 2.9.
При этом ставится задача определить интервалы времени τ между моментами проведения двух последовательных технических инспекций методами неразрушающего контроля, при которых вероятность разрушения не превысит предельно допустимой величины вероятности разрушения, которая в рассматриваемом примере выбирается на уровне [PF] = 5.0 × 10–5 для трех расчетных случаев, когда значения математического ожидания пропущенного в эксплуатацию после неразрушающего контроля глубины трещины равны соответственно: E{a0} = 1 × 10–3 м, E{a0} = 1.5 × 10–3 м и E{a0} = 2 × 10–3 м.
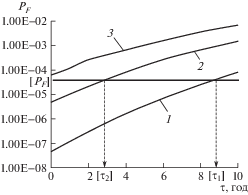
На рис. 5 представлены зависимости вероятности разрушения от промежутка времени между техническими инспекциями (τ) для указанных трех случаев. Из рис. 5 следует, что при избранной величине [PF] в случае 1 (когда E{a0} = 1 × 10–3 м) интервал времени между проведением инспекций можно выбрать равным [τ1] = 8 лет и, соответственно, предельно допустимое число циклов нагружения [N1] = ν[τ1] = 4000 циклов; для случая 2 (когда E{a0} = 1.5 × 10–3 м): [τ2] = 2 года и [N2] = 1000 циклов; а в случае 3 (когда E{a0} = 2 × 10–3 м) эксплуатация рассматриваемого элемента запрещена, поскольку уже в момент ввода элемента в эксплуатацию вероятность его разрушения превышает предельно допустимую величину.
Рис. 5.
Зависимости вероятности усталостного разрушения элемента для трех случаев: E{a0} = 1 × 10–3 м (кривая 1); E{a0} = 1.5 × 10–3 м (кривая 2) и E{a0} = 2 × 10–3 м (кривая 3).
Если вместо экспоненциального распределения (3) величины a0 аналогично тому, как это делалось в п. 2, использовать физически более корректное усеченное экспоненциальное распределение (7), то после аналогичных преобразований можно получить уточненное выражение для вероятности усталостного разрушения конструктивного элемента с трещиной
(16)
$\begin{gathered} {{P}_{F}}({{\tau }_{N}}) = \int\limits_{{{K}_{{Ic\min }}}}^{{{K}_{{Ic\max }}}} {\frac{1}{{\sqrt {2\pi } S\{ {{K}_{{Ic}}}\} }}{{e}^{{ - \frac{{{{{({{K}_{{Ic}}} - E\{ {{K}_{{Ic}}}\} )}}^{2}}}}{{2S{{{\{ {{K}_{{Ic}}}\} }}^{2}}}}}}}} \times \\ \times \;\left( {1 - \frac{1}{{1 - {{e}^{{ - \frac{1}{{E\{ {{a}_{0}}\} }}\delta }}}}} + \frac{{{{e}^{{ - \frac{{{{{\left( {{{{\left( {\frac{{{{K}_{{IC}}}(1 - R)}}{{{{f}_{k}}\Delta \sigma \sqrt \pi }}} \right)}}^{{2 - m}}} - NC\left( {1 - \frac{m}{2}} \right){{{\left( {\frac{{{{f}_{k}}}}{{1 - R}}\Delta \sigma \sqrt \pi } \right)}}^{m}}} \right)}}^{{2/(2 - m)}}}}}{{E\{ {{a}_{0}}\} }}}}}}}{{1 - {{e}^{{ - \frac{1}{{E\{ {{a}_{0}}\} }}\delta }}}}}} \right)d{{K}_{{Ic}}}. \\ \end{gathered} $На рис. 6 представлены графики зависимости вероятности разрушения от величины математического ожидания глубины трещины, пропущенной в эксплуатацию после неразрушающего контроля E{a0}, полученные для случаев экспоненциального и усеченного экспоненциального распределения величины a0.
Рис. 6.
Зависимости вероятности разрушения от уровня пропущенной в эксплуатацию дефектности: 1 – для экспоненциального распределения величины a0; 2 – для усеченного экспоненциального распределения a0.
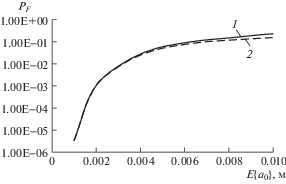
Так как оценки, полученные для случаев экспоненциального (15) и усеченного экспоненциального распределений (16), оказываются весьма близкими, в расчетах можно ориентироваться на более простую зависимость (15).
4. Сопоставление расчетной вероятности разрушения с величиной предельно-допустимой вероятности разрушения. Прочность и ресурс рассматриваемого элемента считаются обеспеченными, если расчетная величина вероятности разрушения PF оказывается меньше предельно допустимой вероятности разрушения [PF]: ${{P}_{F}} < [{{P}_{F}}]$.
Вопрос об обоснованном выборе величины предельно допустимой вероятности разрушения рассматриваемого элемента [PF] решается с учетом критичности данного элемента для обеспечения прочности и безопасности конструкции в целом, а также уровня социальной значимости самой конструкции и величины ущербов, возникающих в случае ее разрушения.
Вероятность разрушения системы в целом (PSF) как вероятность сложного события определяется через произведение вероятности разрушения элемента (PF) и условной вероятности разрушения системы в случае разрушения данного элемента (${{P}_{{SF|F}}}$): ${{P}_{{SF}}} = {{P}_{F}}{{P}_{{SF|F}}}$.
Аналогичное условие можно записать для предельно допустимых вероятностей
Предельная величина вероятности разрушения конструкции в целом [PSF] устанавливается в зависимости от таких факторов как величина ущерба, который может наступить в случае разрушения системы, ее социальной значимости системы и срока эксплуатации [13, 14]. В частности, Международной научно-информационной ассоциацией строительной индустрии (CIRIA – Construction Industry Research and Information Association) для сложных инженерных сооружений (плотин, мостов, шельфовых платформ) принята формула для оценки величины предельно допустимой вероятности разрушения системы
где t – расчетный срок эксплуатации системы; L – среднее количество людей, которые могут погибнуть в случае разрушения системы; kHF – коэффициент, учитывающий разрушения, связанные с человеческим фактором (обычно принимают kHF = 10); ξS – коэффициент социальной значимости системы (табл. 2). Таким образом, величина [PSF] обычно оказывается в диапазоне 1 × 10–5–1 × 10–8.Таблица 2.
Коэффициент социальной значимости для различных типов технических систем [14]
| Тип системы | ξS |
|---|---|
| Объекты массового скопления людей (спортивные комплексы, торговые центры) | 0.005 |
| Плотины | 0.005 |
| Жилые здания, офисные центры, промышленные объекты | 0.05 |
| Мосты | 0.5 |
| Буровые вышки, шельфовые установки | 5 |
Условная вероятность разрушения системы в случае разрушения рассматриваемого элемента (${{P}_{{SF|F}}}$) определяется с помощью графологических методов сценарной оценки (типа методов дерева событий, дерева отказов, байесовых сетей и др.). После чего из выражения (17) определяется предельно допустимая вероятность разрушения рассматриваемого элемента [PF], которая затем сопоставляется с расчетной вероятностью разрушения. Далее принимается решение относительно обеспеченности прочности и ресурса рассматриваемого конструктивного элемента.
Заключение. Разработан метод оценки вероятности разрушения конструктивных элементов технических систем с постулируемой дефектностью. Метод позволяет учитывать различные виды развития трещин, такие как усталостное, коррозионное растрескивание под напряжением или замедленное деформационное коррозионное растрескивание через константы, входящие в уравнение Пэриса. Метод учитывает время эксплуатации, что позволяет определять оптимальную периодичность неразрушающего контроля.
Список литературы
Гетман А.Ф., Козин Ю.Н. Неразрушающий контроль и безопасность эксплуатации сосудов и трубопроводов давления. М.: Энергоатомиздат, 1997. 288 с.
Гетман А.Ф. Ресурс эксплуатации сосудов и трубопроводов АЭС. М.: Энергоатомиздат, 2000. 427 с.
Кузьмин Д.А., Кузьмичевский А.Ю., Верташенок М.В. Остаточная дефектность и вероятность существования дефектов с размером, превышающим допускаемое значение // Строительная механика инженерных конструкций и сооружений. 2020. Т. 16. № 5. С. 414.
BS 7910:2013. Guide to Methods of Assessing the Acceptability of Flaws in Metallic Structures, 3rd ed. BSI: London, UK, December 2013.
Ржаницын А.Р. Расчет сооружений с учетом пластических свойств металлов. М.: Стройиздат, 1979. 289 с.
Ching J. Equivalence between reliability and factor of safety // Probabilistic Engineering Mechanics. 2009. V. 24 (2). P. 159.
Ang A., Tang. W. Probability concepts in Engineering Planning and Design. V. 1. Basic Principles. John Wiley & Sons, Inc. US. 1975. V. 1. 407 p.
Melchers R. Structural Reliability Analysis and Prediction. 2nd Ed. John Wiley &Sons Ltd., England, 1999.
Шатов М.М., Чернявский А.О. Методика назначения предельной вероятности отказа // Проблемы машиностроения и надежности машин. 2013. № 1. С. 51.
Mori Y., Ellingwood B.E. Reliability-based service-life assessment of aging concrete structures // J. Struct. Eng. 1993. V. 119 (5). P. 1600.
Aghakouchak A.A., Stiemer S.F. Fatigue reliability assessment of tubular joints of existing offshore structures // Can. J. Civ. Eng. 2001. V. 28. P. 691.
Kong J.S., Frangopol D.M. Life-cycle performance prediction of steel/concrete composite bridges // International Journal of Steel Structures. 2002. V. 2 (1). P. 13.
Резников Д.О. Соотношение между детерминистическим и вероятностным подходами к оценке конструкционной прочности технических систем // Проблемы машиностроения и автоматизации. 2018. № 3. С. 61.
Elishakoff I. Safety Factors and Reliability: Friends or Foes Kluwer. Academic Publishers, Dordrecht, 2004. 295 p.
Матвиенко Ю.Г. Модели и критерии механики разрушения. М.: Физматлит, 2006. 328 с.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин