Проблемы машиностроения и надежности машин, 2021, № 4, стр. 10-17
Исследование напряженно-деформированного состояния зубьев колес
Ф. Г. Нахатакян 1, *, Ф. И. Плеханов 2
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
2 Ижевский государственный технический университет им. М.Т. Калашникова
Ижевск, Россия
* E-mail: filnahat7@mail.ru
Поступила в редакцию 16.07.2020
После доработки 29.03.2021
Принята к публикации 26.04.2021
Аннотация
Предложен аналитический метод определения податливости зубьев зубчатых колес и коэффициентов неравномерности распределения нагрузки, а также напряжений изгиба. Для решения задачи о напряженно-деформированном состоянии зуба колеса, последний представлен в виде клина с углом развернутости, соответствующим углу профиля эвольвентного зуба. Математическая модель нагруженного зуба представлена в виде неоднородного интегрального уравнения Вольтерра с ядром, зависящим от разности аргументов, которое решено методом операционного исчисления. Использование результатов приведенного исследования при расчете зубчатых передач на прочность позволит более точно определить их несущую способность.
Деформация зубьев колес зависит от их геометрии и оказывает существенное влияние на распределение нагрузки и напряжений в их зацеплениях, а также на виброактивность передачи [1–3]. Причем влияние ее на нагрузочную способность привода является положительным, так как позволяет частично компенсировать неизбежные погрешности изготовления механизма.
Существующие методы определения указанных жесткостных и силовых факторов базируются либо на приближенных расчетах, либо на компьютерном моделировании и численном конечно-элементном анализе, что создает определенные сложности при проектировании и исследовании зубчатых передач [4].
Поэтому является актуальным получение аналитических выражений для определения податливости зубьев зубчатых колес и коэффициентов неравномерности распределения нагрузки и напряжений изгиба, в зависимости от которых находится несущая способность механического привода. Это имеет существенное значение для планетарных и волновых передач, в которых неравномерность распределения силовых факторов по длине зуба накладывается на неравномерность распределения нагрузки и напряжений по потокам мощности [5–7]. В связи с этим, очень важно, особенно на стадии проектирования таких зубчатых редукторов, иметь аналитические методы расчета жесткости (податливости) зубчатых зацеплений и о неравномерности распределения нагрузки и напряжений изгиба (по сути, коэффициента концентрации изгибных напряжений). Поэтому в настоящей статье разработан теоретический метод для определения указанных параметров.
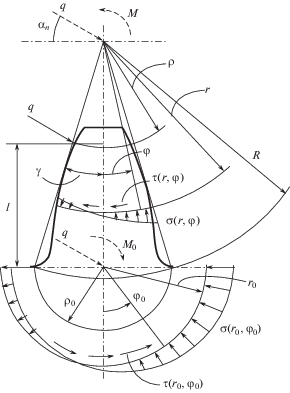
Для аналитического решения задачи о напряженно-деформированном состоянии зуба колеса при равномерном распределении погонной нормальной нагрузки $q$ представим его в виде клина (рис. 1) с углом развернутости $2\gamma $, соответствующим углу профиля эвольвентного зуба в средней его части $\alpha $ и числу зубьев z, и используем известные формулы теории упругости в полярных координатах $r$, $\varphi $, позволяющие определить напряжения изгиба $\sigma (r,\varphi )$ и соответствующие им перемещения.
Применяя к зубу колеса зависимости, справедливые для клина, нагруженного в его вершине, перенесем нагрузку $q$ параллельно самой себе в эту точку, добавив в соответствии с методом Пуансо момент $M = q\cos {{\alpha }_{n}}(\rho \cos \gamma $ + $0.5{{s}_{n}}\operatorname{tg} {{\alpha }_{n}})$ (${{\alpha }_{n}}$ – угол давления, $\rho $ – радиус, соответствующий точке приложения нагрузки; ${{s}_{n}}$ – толщина зуба в месте приложения нагрузки).
Полученный таким образом клинообразный зуб-выступ эквивалентен заданному. Рассмотрим отдельно влияние на него составляющих погонной нагрузки ${{q}_{H}} = q\cos {{\alpha }_{n}}$, ${{q}_{V}} = q\sin {{\alpha }_{n}}$ и момента М.
Напряжения, вызванные действием вертикальной составляющей нагрузки ${{\sigma }_{V}}(r,\varphi )$ = = $\frac{{2q\sin {{\alpha }_{n}}}}{{r\left( {2\gamma + \sin 2\gamma } \right)}}\cos \varphi $, а соответствующее им перемещение точки приложения нагрузки $q$ в направлении линии ее действия
Здесь $\gamma = \arccos \left( {{{{{r}_{b}}} \mathord{\left/ {\vphantom {{{{r}_{b}}} {{{r}_{c}}}}} \right. \kern-0em} {{{r}_{c}}}}} \right) - {{s}_{c}}{\text{/}}2{{r}_{c}}$; $R = \left( {{{l}_{c}}\operatorname{tg} \gamma + 0.5{{s}_{c}}} \right){\text{/}}\sin \gamma $; $\rho = R - l{\text{/}}\cos \gamma $; ${{l}_{c}}$ – расстояние от основания до средней части эвольвентного зуба; $l$ – расстояние от основания зуба до точки приложения нагрузки к нему; ${{s}_{c}}$ – толщина зуба в средней его части; ${{r}_{c}}$ – радиус окружности средней части зубьев колеса; ${{r}_{b}}$ – радиус основной окружности колеса; $E$ – модуль упругости первого рода.
Нормальные напряжения, вызванные действием горизонтальной составляющей нагрузки, и соответствующее им перемещение точки ее приложения в направлении линии действия $q$
Напряжения и перемещение, обусловленные действием момента
Аналогичным образом определяются силовые и деформационные факторы, вызванные податливостью основания зуба. При этом последнее рассматривается как клин с углом развернутости $2{{\gamma }_{0}} = \pi $, нагруженный погонными силами ${{q}_{V}}$, ${{q}_{H}}$ и моментом ${{M}_{0}}$ = ${{q}_{x}}[(R - \rho )\cos \gamma $ – $0.5{{s}_{n}}\operatorname{tg} {{\alpha }_{n}})]$. Тогда
Перемещение, вызванное контактной податливостью зацепления ${{\delta }_{h}}$ (${{\delta }_{h}} = {{k}_{h}}{\text{/}}E$, ${{k}_{h}}$ – коэффициент контактной податливости [8]), ${{\Delta }_{h}} = 0.5q{{\delta }_{h}}$.
Суммарное перемещение точки приложения погонной силы $q$ в направлении линии ее действия, вызванное податливостью зуба
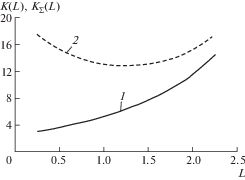
На рис. 2 представлен график зависимости суммарной относительной податливости зуба ${\rm K}(L) = E\Delta {\text{/}}q$ и суммарной относительной податливости однопарного зацепления ${{{\rm K}}_{\Sigma }}(L)$ = ${{\Delta }_{\Sigma }}E{\text{/}}q$ = $(\Delta + \bar {\Delta })E{\text{/}}q$ ($\bar {\Delta }$ – перемещение зуба парного колеса в направлении линии действия $q$) от положения точки приложения нагрузки $L = l{\text{/}}m$ ($m$ – модуль зацепления) при ${{k}_{h}} = 4$. График построен для колес с числом зубьев $z = 50$, коэффициентом смещения исходного контура $x = 0$ и толщиной обода ${{H}_{0}} = 3m$ (рекомендуемая толщина жесткого обода колеса ${{H}_{0}} = 3m{\kern 1pt} - {\kern 1pt} 5m$).
Рис. 2.
Зависимости суммарной относительной удельной податливости зуба зубчатого колеса $K(L)$: линия – 1 и для однопарного зацепления ${{K}_{\Sigma }}(L)$: линия – 2, от положения точки приложения нагрузки L.
Расстояние от основания зуба парного колеса до точки приложения нагрузки к нему $\bar {l}$ определялось исходя из геометрии зацепления [9]
Для установления законов распределения нагрузки $q(x)$ и напряжений изгиба зубьев $\sigma (x)$ по их длине $b$ при наличии угла начального неприлегания $\beta $ рассмотрим напряженно-деформированное состояние зуба с учетом кручения его относительно продольной оси (рис. 3).
Уравнения связи угла начального неприлегания и деформаций зуба имеют следующий вид
(1)
$\begin{gathered} x\Lambda \beta - {{\delta }_{W}}\left[ {q(x) - q(0)} \right] = {{h}_{n}}[\varphi (x) - \varphi (0)] = \frac{{{{h}_{n}}}}{{G{{I}_{K}}}}\int\limits_0^x {\left[ {t(\xi ) - {{h}_{n}}q(\xi )} \right]\left( {x - \xi } \right)d\xi } , \\ \varphi (x) - \varphi (0) = {{\nu }_{F}}\left[ {t\left( x \right) - t\left( 0 \right)} \right], \\ \end{gathered} $Смещение точки приложения нагрузки относительно центра изгиба в основании зуба определим в соответствии с вышеприведенными зависимостями по формуле
Таким образом, разность смещений точек приложения нагрузки к рассматриваемому зубу в произвольном сечении и начале координат в результате его кручения можно выразить через внутренний погонный момент и изгибную податливость
(2)
$x\Lambda \beta - {{\delta }_{W}}\left[ {q(x) - q(0)} \right] = {{\nu }_{F}}{{h}_{n}}\left[ {t\left( x \right) - t\left( 0 \right)} \right] = {{\delta }_{F}}\frac{{t(x) - t(0)}}{{{{h}_{n}}}}.$Интегрирование этого уравнения с учетом уравнения статики $\int_0^b {q(x)dz} $ = $\frac{1}{{{{h}_{n}}}}\int_0^b {t(x)} dx$ = = qb позволяет выразить $t(0)$ через $q(0)$.
Подстановка выражения (2) в равенство (1) дает
где $\psi = {{h}_{n}}\sqrt {\frac{\delta }{{G{{I}_{K}}{{\delta }_{W}}{{\delta }_{F}}}}} $, $\Phi (x) = q(0) + \frac{{\Lambda \beta x}}{{{{\delta }_{W}}}} + 0.5{{\left( {\psi x} \right)}^{2}}\left[ {\frac{{\Lambda \beta }}{\delta }\left( {\frac{{3b - 2x}}{6}} \right) - q} \right]$.Уравнение (3) представляет собой неоднородное интегральное уравнение Вольтерра с ядром, зависящим от разности аргументов, решение которого методом операционного исчисления позволяет найти законы изменения погонной нагрузки и погонного момента с учетом угла перекоса, при контакте зубьев по всей их длине
Найденный погонный момент $t(x)$ можно выразить через нормальные напряжения изгиба в основании зуба (рис. 2), причем зависимость близка к линейной
где ${{\sigma }_{m}}(x)$ – максимальное значение напряжения изгиба в произвольном поперечном сечении зуба; $D$ – коэффициент пропорциональности. Поэтому отношение максимального погонного момента $t(b)$ к среднему $t = q{{h}_{n}}$ можно представить в виде равенства ${{K}_{F}} = {{\sigma }_{m}}(b){\text{/}}{{\sigma }_{m}}$ (${{\sigma }_{m}}$ – среднее значение напряжения изгиба в крайних точках сечения).В соответствии с этим и с учетом приведенных выше соотношений между податливостями зуба и зацепления определим максимальные значения силовых факторов и коэффициенты неравномерности их распределения
На рис. 4, 5 представлены графики изменения относительной нагрузки $Q(X) = q(X){\text{/}}q$, относительного момента $T(X) = t(X){\text{/}}t$ и соответствующих им коэффициентов неравномерности ${{K}_{H}}$ и ${{K}_{F}}$ в зависимости от безразмерных величин $\beta * = \beta bE{\text{/}}q$, $B = b{\text{/}}m$, $X = x{\text{/}}b$.
Рис. 4.
Распределение относительной нагрузки (линия 1) $Q(X)$ и относительного момента изгиба зуба (линия 2) T(X) по его длине при β* = βbE/q = 20, l = 1.25m, b = 10m.
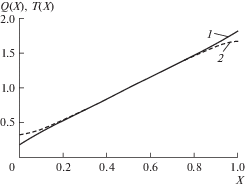
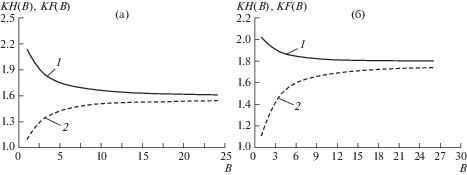
Рис. 5.
Зависимость коэффициентов неравномерности распределения нагрузки (линия 1) KH = KH и напряжений изгиба зуба (линия 2) KF = KF от его относительной длины B = b/m при β* = βbE/q = 20: (а) – приложение нагрузки к вершине зуба (l = 2.25m); (б) – приложение нагрузки в полюсе зацепления (l = 1.25m).
Для определения коэффициентов неравномерности распределения нагрузки и напряжений изгиба K при произвольных значениях величин β* и B с использованием графиков рис. 5 следует воспользоваться выражением, записанным с учетом линейного характера изменения указанных коэффициентов от угла начального неприлегания зубьев
Анализ приведенных выше выражений и построенных по ним графиков показывает, что напряжения изгиба (или соответствующий им изгибающий момент) в отличие от нагрузки распределяются по длине зуба более равномерно. Это обусловлено кручением зуба и появлением в результате этого касательных напряжений в сечениях, перпендикулярных продольной оси $x$. Указанные напряжения создают поддерживающий эффект, передавая изгибающий момент от одного сечения к другому. При относительном угле начального неприлегания зубьев $\beta * = \beta bE{\text{/}}q \leqslant 50$ и их длине $b \geqslant 10m$ коэффициент неравномерности распределения нагрузки превышает коэффициент неравномерности распределения напряжений изгиба не более чем на 20%, при $b \geqslant 20m$ – не более чем на 11%. С ростом $\beta {\text{*}}$ разница указанных коэффициентов неравномерности возрастает.
Использование полученных зависимостей при расчете зубчатых передач на прочность позволяет с высокой степенью точности определить их несущую способность.
Выводы. 1. Деформативность зубьев колес и коэффициенты неравномерности распределения нагрузки и напряжений изгиба в значительной степени зависят от фазы однопарного зацепления, но мало изменяются с изменением наиболее часто используемых на практике значений коэффициентов смещения исходного контура и чисел зубьев колес. 2. При отношении длины зуба к модулю зацепления не менее 20 и относительном угле начального неприлегания зубьев $\beta * \leqslant 50$ коэффициент неравномерности распределения нагрузки превышает коэффициент неравномерности распределения напряжений изгиба не более чем на 11%. 3. С ростом относительного угла начального неприлегания зубьев и уменьшением их длины разница коэффициентов неравномерности распределения нагрузки и напряжений изгиба возрастает.
Список литературы
Ражиков В.Н., Беляев А.Н. Учет деформации подшипников сателлитов при проверке геометрических показателей качества зацепления в цилиндрических эвольвентных зубчатых передачах внутреннего зацепления с малой разностью чисел зубьев // Вестник машиностроения. 2017. № 2. С. 38.
Plekhanov F.I., Pushkarev A.E., Pushkarev I.A. Influence of Layout Features and Parameters of a Planetary Gear on Its Dynamics and Strength Characteristics // Mechanisms and Machine Science. Springer. 2018. V. 51. P. 481.
Ан И.К. Распределение усилий между звеньями планетарного механизма типа K-H-V // Вестник машиностроения. 2016. № 5. С. 60.
Drewniak I., Kopek I., Zawislak S. Kinematical and Efficiency Analysis of Planetary Gear Trains by Means of Various Graph-Based Approaches // Theory and Practice of Gearing and Transmissions. Mechanisms and Machine. Springer. 2016. V. 34. P. 263.
Plekhanov F.I., Goldfarb V.I., Vychuzhanina E.F. Load Distribution in Meshing of Planetary Gearweels and Its Influence on the Technical and Economic Performance of the Mechanism // Mechanisms and Machine Science. Springer. 2018. V. 51. P. 117.
Тимофеев Г.А. Проектирование приводов с двухступенчатыми волновыми зубчатыми передачами для следящих систем // Проблемы машиностроения и надежности машин. 2016. № 5. С. 32.
Волков Г.Ю., Колмаков С.В. Структурный синтез безводильных планетарных передач // Вестник машиностроения. 2014. № 4. С. 26.
Нахатакян Ф.Г., Нахатакян Д.Ф. Расчетный метод определения суммарной контактной деформации упругих тел конечных размеров на линейном контакте // Приводы и компоненты машин. 2016. № 1–2 (19). С. 17.
Plekhanov F.I., Goldfarb V.I. Rational Designs of planetary Transmissions, Geometry of gearing and Strength Parameters // Theory and Practice of Gearing and Transmissions. Mechanisms and Machine. Springer. 2016. V. 34. P. 285.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин