1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2021

Проблемы машиностроения и надежности машин, 2021, № 5, стр. 33-40

Математическая модель смазочного материала в опоре скольжения с плавким покрытием и учетом зависимости вязкости от давления при неполном заполнении рабочего зазора

Д. У. Хасьянова 1, *, М. А. Мукутадзе 2, **, А. М. Мукутадзе 2, Н. С. Задорожная 2

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

* E-mail: dinara.khasyanova@mail.ru
** E-mail: murman1963@yandex.ru

Поступила в редакцию 05.02.2021
После доработки 11.06.2021
Принята к публикации 24.06.2021

Полный текст (PDF)

Аннотация

В статье представлено асимптотическое и точное автомодельное решение для нулевого (без учета расплава) и первого (с учетом расплава) приближения клиновидной опоры скольжения адаптированного к условиям трения опорным профилем ползуна и легкоплавким металлическим покрытием поверхности направляющей при учете зависимости реологических свойств смазочного материала и расплава, которые обладают при ламинарном режиме течения истинно-вязкими свойствами от давления. Получены аналитические зависимости для профиля расплавленной поверхности легкоплавкого металлического покрытия направляющей, а также для поля скоростей и давлений при нулевом и первом приближении.

Ключевые слова: гидродинамика, опора скольжения (ползун, направляющая), вязкий несжимаемый жидкий смазочный материал, расплавленная поверхность направляющей, зависимость вязкости смазочного материала от давления, нестандартная опорная поверхность ползуна

Разработке расчетной модели упорных подшипников скольжения с легкоплавким покрытием посвящено значительное количество работ [1–5]. Однако процесс смазывания на расплавах покрытий не является самоподдерживающимся процессом. Для обеспечения самоподдерживающегося процесса смазывания подшипников скольжения возникает необходимость не только в наличии легкоплавкого покрытия на одной из контактных поверхностей, но и постоянного наличия смазочного материала, которое можно обеспечить при постоянной его подаче или пористым покрытием на другой контактной поверхности [6–8], а также нестандартным опорным профилем.

В настоящей статье для обеспечения самоподдерживающегося процесса и гидродинамического режима течения приводится расчетная модель клиновидной опоры скольжения “ползун–направляющая” с нестандартным опорным профилем ползуна и легкоплавким покрытием поверхности направляющей. Определены основные рабочие характеристики рассматриваемой пары трения – несущая способность и сила трения. Дана оценка влияния параметров, обусловленных расплавом покрытия, адаптированным к условиям трения опорным профилем и параметре, характеризующем зависимость вязкости смазочного материала от давления на несущую способность и силу трения.

Методика расчета. Рассматривается движение вязкой жидкости и расплава покрытия в рабочем зазоре клиновидной опоры скольжения. При этом направляющая с легкоплавким покрытием перемещается со скоростью u*, а наклонный ползун с нестандартным опорным профилем неподвижен (рис. 1).

Рис. 1.

Рабочая схема: 1 – контур наклонного ползуна (пяты); 2 – контур расплавленного подпятника; 3 – контур нестандартного опорного профиля.

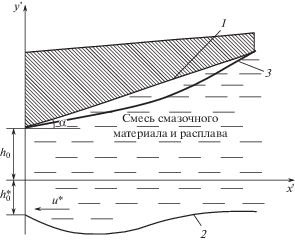
Расчетная схема представлена в системе координат $x{\kern 1pt} '{\kern 1pt} o{\kern 1pt} '{\kern 1pt} y{\kern 1pt} '$. Контуры наклонного ползуна с нестандартным опорным профилем и расплавленного покрытия поверхности направляющей обозначены следующим образом:

(1)
$y{\kern 1pt} ' = {{h}_{0}} + x{\kern 1pt} '\operatorname{tg} \alpha *,\quad y{\kern 1pt} ' = {{h}_{0}} + x{\kern 1pt} '\operatorname{tg} \alpha {\kern 1pt} * - \;a{\kern 1pt} '\sin \omega {\kern 1pt} '{\kern 1pt} x{\kern 1pt} ' = h{\kern 1pt} '\left( {x{\kern 1pt} '} \right),\quad y{\kern 1pt} ' = - \lambda {\kern 1pt} '{\kern 1pt} f{\kern 1pt} '\left( {x{\kern 1pt} '} \right),$
где α* – угол между наклонным ползуном и осью Ох; h0 – толщина смазочного слоя в начальном сечении; $a{\kern 1pt} '$ и $\omega {\kern 1pt} '$ – амплитуда возмущения и параметр адаптированного профиля ползуна соответственно.

Зависимость вязкости от давления задается следующим выражением

(2)
$\mu {\kern 1pt} ' = {{\mu }_{0}}{{е}^{{\tilde {\alpha }р'}}},$
где μ0 – характерная вязкость; $\mu {\kern 1pt} '$ – коэффициент динамической вязкости смазочного материала; $р{\kern 1pt} '$ – гидродинамическое давление в смазочном слое; $\tilde {\alpha }$ – постоянная.

Рассматриваются условия движения бесконечно широкого ползуна при следующих допущениях: 1) жидкая среда является несжимаемой жидкостью; 2) все тепло в рабочем зазоре идет на плавление поверхностью покрытия.

Исходными базовыми уравнениями являются общеизвестное уравнение для “тонкого слоя” движения смазочного материала с учетом (1), уравнение неразрывности, а также уравнение, описывающее профиль расплавленного контура покрытия поверхности направляющей с учетом скорости диссипации механической энергии

(3)
$\begin{gathered} \frac{{\partial p{\kern 1pt} '}}{{\partial x{\kern 1pt} '}} = 0;\quad \mu {\kern 1pt} '\frac{{{{\partial }^{2}}{{{v}}_{{x'}}}}}{{\partial y{\kern 1pt} {{'}^{2}}}} = \frac{{dp{\kern 1pt} '}}{{dx{\kern 1pt} '}};\quad \frac{{\partial {{{v}}_{{x'}}}}}{{\partial x{\kern 1pt} '}} + \frac{{\partial {{{v}}_{{y'}}}}}{{\partial y{\kern 1pt} '}} = 0; \\ \frac{{d\lambda {\kern 1pt} '{\kern 1pt} f{\kern 1pt} '\left( {x{\kern 1pt} '} \right)}}{{dx{\kern 1pt} '}}u{\kern 1pt} *{\kern 1pt} L{\kern 1pt} ' = - 2\mu {{\int\limits_{ - \lambda {\kern 1pt} '{\kern 1pt} f{\kern 1pt} '\left( {x'} \right)}^{h'\left( {x'} \right)} {\left( {\frac{{\partial {{{v}}_{{x'}}}}}{{\partial y{\kern 1pt} '}}} \right)} }^{2}}dy, \\ \end{gathered} $
где ${{{v}}_{{x'}}}$, ${{{v}}_{{y'}}}$ – компоненты вектора скорости смазочной среды; $L{\kern 1pt} '$ – удельная теплота плавления на единицу объема.

Граничные условия для исходного уравнения (3) с учетом общепринятых упрощений запишутся в виде

(4)
$\begin{gathered} {{{v}}_{{x'}}} = 0,\quad {{{v}}_{{y'}}} = 0\quad {\text{при}}\quad y = {{h}_{0}} + x{\kern 1pt} '\operatorname{tg} \alpha - a{\kern 1pt} '\sin \omega {\kern 1pt} '{\kern 1pt} x{\kern 1pt} '; \\ {{{v}}_{{x'}}} = u*,\quad {{{v}}_{{y'}}} = 0\quad {\text{при}}\quad y = - \lambda {\kern 1pt} '{\kern 1pt} f{\kern 1pt} '\left( {x{\kern 1pt} '} \right); \\ p{\kern 1pt} '\left( 0 \right) = p{\kern 1pt} '\left( L \right) = {{p}_{a}}. \\ \end{gathered} $

Переход к безразмерным переменным осуществим соотношениями

(5)
$\begin{gathered} x{\kern 1pt} ' = Lx,\quad y{\kern 1pt} ' = {{h}_{0}}y,\quad {{{v}}_{{x''}}} = u{\kern 1pt} *{\kern 1pt} {v},\quad {{{v}}_{{y'}}} = u{\kern 1pt} *{\kern 1pt} \frac{{{{h}_{0}}}}{L}u,\quad p{\kern 1pt} ' = p{\kern 1pt} *{\kern 1pt} p, \\ \omega {\kern 1pt} ' = \omega L,\quad p* = \frac{{\mu u{\kern 1pt} *{\kern 1pt} L}}{{h_{0}^{*}}},\quad \mu {\kern 1pt} ' = {{\mu }_{0}}\mu ,\quad \alpha = p{\kern 1pt} *{\kern 1pt} \tilde {\alpha }. \\ \end{gathered} $

С учетом (5) уравнения (3) и граничные условия (4) примут вид

(6)
$\frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}} = {{e}^{{ - \alpha p}}}\frac{{dp}}{{dx}};\quad \frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0;\quad \frac{{d\Phi \left( x \right)}}{{dx}} = - K\int\limits_{ - \Phi \left( x \right)}^{h\left( x \right)} {{{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}}^{2}}dy,} $
(7)
$\begin{gathered} {v} = 0,\quad u = 0\quad {\text{при}}\quad y = 1 + \eta x - {{\eta }_{1}}\sin \omega x = h\left( x \right); \\ {v} = - 1,\quad u = 0\quad {\text{при}}\quad y = - \Phi \left( x \right);\quad p\left( 0 \right) = p\left( 1 \right) = \frac{{{{p}_{a}}}}{{p{\kern 1pt} *}}; \\ \end{gathered} $
где $K = \frac{{2{{\mu }_{0}}u{\kern 1pt} *{\kern 1pt} L}}{{h_{0}^{*}L{\kern 1pt} '}}$, $\eta = \frac{{L\operatorname{tg} \alpha }}{{{{h}_{0}}}}$, ${{\eta }_{1}} = \frac{{a{\kern 1pt} '}}{{{{h}_{0}}}}$, $\Phi \left( x \right) = \eta {}_{1}f\left( x \right)$.

В результате преобразования система уравнения (6) примет вид

(8)
$\frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}} = - \frac{1}{\alpha }\frac{{dz}}{{dx}};\quad \frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0;\quad z\frac{{d\Phi \left( x \right)}}{{dx}} = K\int\limits_{ - \Phi \left( x \right)}^{h\left( x \right)} {{{{\left( {\frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}}dy} ,$
с граничными условиями

(9)
$\begin{gathered} {v} = 0,\quad u = 0\quad {\text{при}}\quad y = 1 + \eta x - {{\eta }_{1}}\sin \omega x; \\ {v} = - 1,\quad u = 0\quad {\text{при}}\quad y = - \Phi \left( x \right);\quad {{z}_{1}}\left( 0 \right) = {{z}_{1}}\left( 1 \right) = {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}. \\ \end{gathered} $

Функцию Ф(х) разложим по параметру K, обусловленному расплавом поверхности покрытия направляющей

(10)
$\Phi \left( x \right) = - {{\Phi }_{0}}\left( x \right) - K{{\Phi }_{1}}\left( x \right) - {{K}^{2}}{{\Phi }_{2}}\left( x \right) - {{K}^{3}}{{\Phi }_{3}}\left( x \right) - \ldots = H\left( x \right).$

Граничные условия для компонентов скорости на контуре $y = - \Phi \left( x \right)$ запишем в виде

(11)
$\begin{gathered} {v}\left( {0 - H\left( x \right)} \right) = {v}\left( 0 \right) - {{\left. {\left( {\frac{{\partial {v}}}{{\partial y}}} \right)} \right|}_{{y = 0}}} \cdot H - {{\left. {\left( {\frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}}} \right)} \right|}_{{y = 0}}} \cdot {{H}^{2}} + \ldots = - 1; \\ u\left( {0 - H\left( x \right)} \right) = u\left( 0 \right) - {{\left. {\left( {\frac{{\partial u}}{{\partial y}}} \right)} \right|}_{{y = 0}}} \cdot H - {{\left. {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}} \right)} \right|}_{{y = 0}}} \cdot {{H}^{2}} + \ldots = 0. \\ \end{gathered} $

Асимптотическое решение системы уравнений (8)–(10) с учетом граничных условий (9) и (11) ищем в виде

${v}\left( {x,y} \right) = {{{v}}_{0}}\left( {x,y} \right) + K{{{v}}_{1}}\left( {x,y} \right) + {{K}^{2}}{{{v}}_{2}}\left( {x,y} \right) + \ldots ;$
(12)
$\begin{gathered} u\left( {x,y} \right) = {{u}_{0}}\left( {x,y} \right) + K{{u}_{1}}\left( {x,y} \right) + {{K}^{2}}{{u}_{2}}\left( {x,y} \right) + \ldots ; \\ \Phi \left( x \right) = {{\Phi }_{0}}\left( x \right) - K{{\Phi }_{1}}\left( x \right) - {{K}^{2}}{{\Phi }_{2}}\left( x \right) - {{K}^{3}}{{\Phi }_{3}}\left( x \right) - \ldots ; \\ \end{gathered} $
$z\left( x \right) = {{z}_{0}}\left( x \right) + K{{z}_{1}}\left( x \right) + {{K}^{2}}{{z}_{2}}\left( x \right) + {{K}^{3}}{{z}_{3}}\left( x \right) \ldots .$

Выполняя подстановку (12) в систему уравнений (8) с учетом граничных условий (9), получим систему уравнений и граничные условия к ней:

– для нулевого приближения

(13)
$\frac{{{{\partial }^{2}}{{{v}}_{0}}}}{{\partial {{y}^{2}}}} = - \frac{1}{\alpha }\frac{{d{{z}_{0}}}}{{dx}},\quad \frac{{\partial {{{v}}_{0}}}}{{\partial x}} + \frac{{\partial {{u}_{0}}}}{{\partial y}} = 0,$
с граничными условиями
(14)
$\begin{gathered} {{{v}}_{0}} = 0,\quad {{u}_{0}} = 0,\quad {\text{при}}\quad y = 1 + \eta x - {{\eta }_{1}}\sin \omega x; \\ {{{v}}_{0}} = - 1,\quad {{u}_{0}} = 0\quad {\text{при}}\quad y = - \Phi \left( x \right);\quad {{z}_{0}}\left( 0 \right) = {{z}_{0}}\left( 1 \right) = {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}; \\ \end{gathered} $
– для первого приближения
(15)
$\frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{y}^{2}}}} = - \frac{1}{\alpha }\frac{{d{{z}_{1}}}}{{dx}};\quad \frac{{\partial {{{v}}_{1}}}}{{\partial x}} + \frac{{\partial {{u}_{1}}}}{{\partial y}} = 0;\quad - {\kern 1pt} {{z}_{0}}\frac{{d{{\Phi }_{1}}\left( x \right)}}{{dx}} = \int\limits_{ - \Phi \left( x \right)}^{h\left( x \right)} {{{{\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right)}}^{2}}dy} ,$
с граничными условиями

${{{v}}_{1}} = {{\left. {\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}} \cdot \tilde {\Phi };\quad {{u}_{1}} = {{\left. {\left( {\frac{{\partial {{u}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}} \cdot \tilde {\Phi };$
(16)
${{{v}}_{1}} = 0\quad {{u}_{1}} = 0\quad {\text{при}}\quad h\left( x \right) = 1 + \eta x - {{\eta }_{1}}\sin \omega x;$
${{z}_{1}}\left( 0 \right) = {{z}_{1}}\left( 1 \right) = 0;\quad {{\Phi }_{1}}\left( 0 \right) = h_{0}^{*}.$

Автомодельное решение системы (13) и (14) (для нулевого приближения) будем искать в виде

(17)
$\begin{gathered} {{{v}}_{0}} = \frac{{\partial {{\psi }_{0}}}}{{\partial y}} + {{V}_{0}}\left( {x,y} \right);\quad {{u}_{0}} = - \frac{{\partial {{\psi }_{0}}}}{{\partial x}} + {{U}_{0}}\left( {x,y} \right);\quad {{\psi }_{0}}\left( {x,y} \right) = {{{\tilde {\psi }}}_{0}}\left( \xi \right);\quad \xi = \frac{y}{{h\left( x \right)}}; \\ {{V}_{0}}\left( {x,y} \right) = {\tilde {v}}\left( \xi \right);\quad {{U}_{0}}\left( {x,y} \right) = \tilde {u}\left( \xi \right)h{\kern 1pt} '\left( x \right). \\ \end{gathered} $

Подставляя выражение (17) в систему уравнений (13) с учетом условий (14), получим систему уравнений и граничные условия к ней

(18)
$\tilde {\psi }{{_{0}^{{'''}}}_{0}} = {{\tilde {С}}_{2}},\quad {\tilde {v}}_{0}^{{''}} = {{\tilde {С}}_{1}},\quad \tilde {u}_{0}^{'} + \xi {\tilde {v}}_{0}^{'} = 0;\quad \frac{{d{{z}_{0}}}}{{dx}} = - \alpha \left[ {\frac{{{{{\tilde {С}}}_{1}}}}{{{{{\tilde {h}}}^{2}}\left( x \right)}} + \frac{{{{{\tilde {С}}}_{2}}}}{{{{{\tilde {h}}}^{3}}\left( x \right)}}} \right];$
(19)
$\begin{gathered} \tilde {\psi }_{0}^{'}\left( 0 \right) = 0,\quad \tilde {\psi }_{0}^{'}\left( 1 \right) = 0,\quad \tilde {u}_{0}^{'}\left( 1 \right) = 0;\quad {\tilde {v}}_{0}^{'}\left( 1 \right) = 0; \\ {{{\tilde {u}}}_{0}}\left( 0 \right) = 0;\quad {{{{\tilde {v}}}}_{0}}\left( 0 \right) = - 1;\quad \int\limits_0^1 {{{{{\tilde {v}}}}_{0}}\left( \xi \right)} d\xi = 0. \\ \end{gathered} $

Выполняя интегрирование (18)–(19), получим расчетные формулы

(20)
$\begin{gathered} \tilde {\psi }_{0}^{'}\left( \xi \right) = \frac{{{{{\tilde {С}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right);\quad {{{{\tilde {v}}}}_{0}}\left( \xi \right) = {{{\tilde {С}}}_{1}}\frac{{{{\xi }^{2}}}}{2} + \left( {1 - \frac{{{{{\tilde {С}}}_{1}}}}{2}} \right)\xi + 1; \\ {{{\tilde {u}}}_{0}} = \frac{{d\tilde {\psi }}}{{d\xi }}\frac{\varepsilon }{{\tilde {h}\left( x \right)}} + \frac{{\xi {{{v}}_{0}}}}{\eta } - \frac{1}{\eta }\int\limits_0^\xi {{{{v}}_{0}}} \left( \xi \right)d\xi ,\quad {{{\tilde {C}}}_{1}} = 6. \\ \end{gathered} $

Из условия ${{z}_{0}}\left( 0 \right) = {{z}_{0}}\left( 1 \right) = {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}$ для ${{\tilde {С}}_{2}}$ получим

(21)
${{\tilde {С}}_{2}} = - 6\left( {1 + \frac{{{\eta }}}{2} + \frac{{{{{{\eta }}}_{1}}}}{\omega }\left( {\cos \omega - 1} \right)} \right).$

С учетом (21) для z0 получим

(22)
${{z}_{0}} = - 6\alpha \left( {\frac{\eta }{2}\left( {{{x}^{2}} - x} \right) + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos \omega x - 1} \right) - \left( {\cos \omega - 1} \right)x} \right) + {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}.$

Для функции ${{\Phi }_{1}}\left( x \right)$, определяющей расплавленный контур опорного кольца, с учетом (20) получим

(23)
$\frac{{d{{\Phi }_{1}}\left( x \right)}}{{dx}} = \frac{{h\left( x \right)}}{{{{z}_{0}}}}{{\int\limits_0^1 {\left( {\frac{{\psi _{0}^{{''}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{{\tilde {v}}_{0}^{'}\left( \xi \right)}}{{h\left( x \right)}}} \right)} }^{2}}d\xi .$

Выполняя интегрирование (23), получим

(24)
${{\Phi }_{1}}\left( x \right) = \frac{1}{{\mathop {\sup }\limits_{x \in \left[ {0;1} \right]} }}\left[ {x - \frac{1}{2}\eta {{x}^{2}} - \frac{{{{\eta }_{1}}}}{\omega }\cos \omega x} \right] + h_{0}^{*};$
(25)
$\tilde {\Phi } = \mathop {\sup }\limits_{x \in \left[ {0;1} \right]} {{\Phi }_{1}}\left( x \right).$

Автомодельное решение (15) и (16) будем искать так же, как и для системы уравнений (13) и (14). В результате для поля скоростей и давлений получим расчетные формулы

$\tilde {\psi }{{_{1}^{'}}_{1}}\left( \xi \right) = \frac{{{{{\tilde {\tilde {С}}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right),\quad {{{\tilde {v}}}_{1}}\left( \xi \right) = {{\tilde {\tilde {С}}}_{1}}\frac{{{{\xi }^{2}}}}{2} + \left( {1 - \frac{{{{{\tilde {\tilde {С}}}}_{1}}}}{2}} \right)\xi + 1,\quad {{\tilde {\tilde {C}}}_{1}} = 6M.$
(26)
${{\tilde {\tilde {С}}}_{2}} = - 6M\left( {1 + \frac{{\text{1}}}{2}{{\tilde {\eta }}} + \frac{{{{{{{\tilde {\eta }}}}}_{1}}}}{\omega }\left( {\cos \omega - 1} \right)} \right)\left( {1 + \tilde {\Phi }} \right),$
${{z}_{1}} = \frac{{ - 6\alpha M}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}\left( {\frac{{\tilde {\eta }}}{2}\left( {{{x}^{2}} - x} \right) - \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos \omega x - 1 - \left( {\cos \omega - 1} \right)x} \right)} \right),$
где $\tilde {\eta } = \frac{\eta }{{1 + \tilde {\Phi }}}$, ${{\tilde {\eta }}_{1}} = \frac{{{{\eta }_{1}}}}{{1 + \tilde {\Phi }}}$,

$M = \mathop {\sup }\limits_{x \in \left[ {0;1} \right]} \left| {{{{\left. {\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right)} \right|}}_{{y = 0}}}{{\Phi }_{1}}\left( x \right)} \right| = \mathop {\sup }\limits_{x \in \left[ {0;1} \right]} \left| {\left( {1 + 2\eta x + 4{{\eta }_{1}}\sin \omega x - \frac{3}{2}\eta + \frac{{3{{\eta }_{1}}}}{\omega }\left( {\cos \omega - 1} \right)} \right)} \right|\tilde {\Phi }.$

Для $z = {{z}_{0}} + K{{z}_{1}}$ получим

(27)
$z = - 6\alpha A + {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}} - 6\alpha KM \cdot B,$
где
$A = - \left( {\eta \left( {{{x}^{2}} - x} \right) + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos \omega x - 1} \right) - x\left( {\cos \omega - 1} \right)} \right);$
$B = \frac{{\tilde {\eta }\left( {{{x}^{2}} - x} \right) + \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos \omega x - 1 - x\left( {\cos \omega - 1} \right)} \right)}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}.$

Применяя метод Тейлора для ${{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}$, ${{e}^{{ - \alpha p}}}$, с точностью до $O\left( {{{\alpha }^{3}}} \right)$, $O{{\left( {\frac{{{{p}_{a}}}}{{p{\text{*}}}}} \right)}^{2}}$ для гидродинамического давления получим

(28)
$p = \frac{{{{p}_{a}}}}{{p{\kern 1pt} *}} - 6\left( {A + KMB} \right)\left( {1 + \alpha \frac{{{{p}_{a}}}}{{p{\kern 1pt} *}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{a}}}}{{p{\kern 1pt} *}}} \right)}}^{2}}} \right).$

С учетом (13), (15) и (28) для несущей способности и силы трения получим

$W = p{\kern 1pt} *{\kern 1pt} L\int\limits_0^1 {\left( {p--\frac{{{{p}_{a}}}}{{p{\kern 1pt} *}}} \right)dx} = \frac{{{{\mu }_{0}}{{L}^{2}}u{\kern 1pt} *}}{{h_{0}^{2}}}\left( {\frac{{1 + KM}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}} \right)\left( {1 + \alpha \frac{{{{p}_{a}}}}{{p{\kern 1pt} *}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{a}}}}{{p{\kern 1pt} *}}} \right)}}^{2}}} \right);$
(29)
${{L}_{{{\text{тр}}}}} = \mu \int\limits_0^1 {\left[ {{{{\left. {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right|}}_{{y = 0}}} + K{{{\left. {\frac{{\partial {v}}}{{\partial y}}} \right|}}_{{y = 0}}}} \right]} dx = $
$ = {{\mu }_{0}}\left( {1 - \alpha p + \frac{{{{\alpha }^{2}}{{p}^{2}}}}{2}} \right)\left[ {1 - \frac{\eta }{2} - \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos \omega - 1} \right) - } \right.\left. {K\tilde {\Phi }\left( {1 - \eta - \frac{{2{{\eta }_{1}}}}{\omega }\left( {\cos \omega - 1} \right)} \right)} \right].$

Численный анализ позволил построить зависимости влияния параметров ω, характеризующего адаптированный профиль, и α, характеризующего вязкость на несущую способность подшипника и силу трения (рис. 2).

Рис. 2.

Влияние параметров ω, характеризующего адаптированный профиль, и α, характеризующего вязкость на: несущую способность подшипника – (а); силу трения – (б).

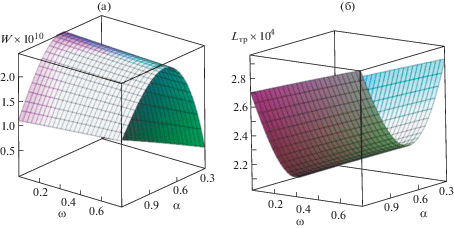
Выводы. Для подшипника с клиновидным зазором и гидродинамическим смазыванием получена уточненная расчетная модель при учете зависимости вязкости смазочного материала и расплава покрытия, обладающих истинно вязкими реологическими свойствами, от давления при ламинарном режиме смазывания и адаптированного к условиям трения опорным профилем ползуна.

Показан значительный вклад параметров: α, характеризующего вязкость; K, обусловленного расплавом покрытия; ω, характеризующего адаптированный опорный профиль. Установлено, что несущая способность подобных опор скольжения превышает на 12–14% этот же параметр у стандартных подшипников скольжения. Коэффициент трения при этом ниже на 15–17%.

Заключение. Разработаны новые многопараметрические выражения для основных рабочих характеристик (несущая способность и сила трения) клиновидной опоры скольжения с учетом реологических свойств истинно вязкого смазочного материала и расплава поверхности направляющей, покрытой легкоплавким металлическим сплавом, с учетом адаптированного к условиям трения опорного профиля ползуна.

Дана оценка влияния параметров переменных факторов, обусловленных расплавом поверхности направляющей, адаптированным к условиям трения опорным профилем ползуна и зависимости вязкости смазочного материала от давления.

Полученные уточненные расчетные модели клиновидных опор скольжения позволяют в результате варьирования покрытия из легкоплавкого металлического покрытия и адаптированного к условиям трения опорного профиля ползуна регулировать соотношение его несущей способности и коэффициента трения.

Установлена удовлетворительная сходимость теоретических и экспериментальных исследований в подтверждение сделанных теоретических выводов, а также получена более упрощенная и точная модель клиновидных опор скольжения с результатами, выполненными в работах [9, 10]

Список литературы

  1. Уилсон Р. Смазка с расплавом // Проблемы трения и смазки. 1976. № 1. С. 19.

  2. Беретта А., Ниро Д., Сильвестри Ф. Подшипники скольжения, смазываемые собственным расплавом или продуктом сублимации // Труды Амер. о-ва инж.-мех. 1992. № 1. С. 86.

  3. Приходько В.М., Котельницкая Л.И. Математическая модель гидродинамической смазки при плавлении опорной поверхности радиального подшипника // Трение и износ. 2001. Т. 22. № 6. С. 606.

  4. Chapple W.M. Mechanics of thin-skinned fold-and-thrust belts // Bulletin of the Geological Society of America. 1978. V. 89. Is. 8. P. 1189. https://doi.org/10.1130/0016-7606(1978)89<1189:MOTFB>2.0.CO;2

  5. Parness A., Soto D., Esparza N., Gravish N., Wilkinson M., Autumn K., Cutkosky M. A microfabricated wedge-shaped adhesive array displaying gecko-like dynamic adhesion, directionality and long lifetime // Journal of the Royal Society Interface. 2009. V. 6. Is. 41. P. 1223. https://doi.org/10.1098/rsif.2009.0048

  6. Kragelsky I.V. Friction and wear. M.: Mechanical engineering, 1968.

  7. Mukutadze M.A., Khasyanova D.U. Optimization of the supporting surface of a slider bearing according to the load-carrying capacity taking into account the lubricant viscosity depending on pressure and temperature // Journal of Machinery Manufacture and Reliability. 2018. V. 4. P. 356.

  8. Ахвердиев К.С., Лагунова Е.О., Василенко В.В. Расчетная модель радиального подшипника, смазываемого расплавом, с учетом зависимости вязкости от давления // Вестник ДГТУ. 2017. № 3 (90). С. 27.

  9. Chigira M., Tsou C.-Y., Matsushi Y., Hiraishi N., Matsuzawa M. Topographic precursors and geological structures of deep-seated catastrophic landslides caused by Typhoon Talas // Geomorphology. 2013. V. 201. P. 479. https://doi.org/10.1016/j.geomorph.2013.07.020

  10. Mahato A., Guo Y., Sundaram N.K., Chandrasekar S. Surface folding in metals: A mechanism for delamination wear in sliding. Proceedings of the Royal Society A // Mathematical, Physical and Engineering Sciences. 2014. V. 470. Is. 2169. https://doi.org/10.1098/rspa.2014.0297

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал