Проблемы машиностроения и надежности машин, 2021, № 6, стр. 73-78

Создание новых перспективных транспортных средств – одна из приоритетных задач современной науки о машинах [1–4]. Важным узлом колесных и гусеничных машин является система подрессоривания [5–8].

В настоящей статье ставится задача построения устройства, в котором можно реализовывать различные подходы к управлению гидравлической системой подрессоривания.

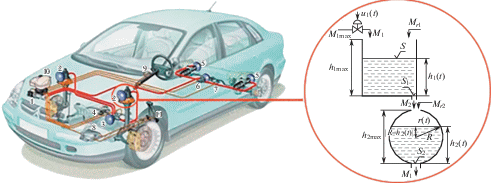
Рассматриваемая гидравлическая система подрессоривания транспортных средств представляет собой совокупность двух резервуаров (рис. 1). Гидравлическую рессору (рис. 1а), можно представить как схему гидравлической системы (рис. 1б).

На рис. 1: h₁(t), м – уровень воды в цилиндрическом резервуаре; h_1max(t), м – максимальный уровень воды в цилиндрическом резервуаре; h₂(t), м – уровень воды в сферическом резервуаре; h_2max(t), м – максимальный уровень воды в сферическом резервуаре; M₁(t), кг/с – массовый приток в цилиндрический резервуар; M₂(t), кг/с – массовый приток в сферический резервуар; M₃ (t), кг/с – массовый отток из сферического резервуара; M_Z1(t), кг/с – изменение массы в цилиндрическом резервуаре; M_Z2(t), кг/с – изменение массы сферического резервуара; u₁(t) – функция входа для массового изменения в цилиндрическом резервуаре; S, м² – площадь дна цилиндрического резервуара; S₁, м² – площадь выходного отверстия цилиндрического резервуара; R, м – диаметр сферического резервуара; S₂, м² – площадь выходного отверстия сферического резервуара.

Для изменения уровней h₁(t) и h₂(t) в соответствии с [11] предполагается

где $\rho $ – плотность жидкости, кг/м³.

Массовый расход M₁(t), M₂(t) и M₃(t) можно описать уравнениями

где k_V1 – константа входного отверстия цилиндрического резервуара, а f(u₁(t)) – характеристическая функция клапана V₁.

Массовый прирост M₁(t) зависит от значения ${{u}_{1}}(t) \in \left[ {0,1} \right]$ M_1max.

Пусть функция f(u₁(t)) будет линейной. Тогда уравнение для массового прироста можно записать как

Уравнение (1), описывает динамику изменения взаимодействия в двух резервуарах [12]

где g – ускорение свободного падения, м/с².

Рассмотрим классический подход к расчету оптимизационной функции управления. Цель управления – снижение уровня вибронагруженности транспортного средства за счет изменения давления (уровня жидкости во втором резервуаре) в гидрорессорах системы подрессоривания.

На входе мы имеем объемно-габаритные, массовые характеристики гидрорессоры, функцию, имитирующую неровности дорожного покрытия (белый шум). Выходом системы является уровень жидкости во втором резервуаре.

Расчет оптимизационной функции управления для k-го шага (являющегося шагом дискретизации) можно рассматривать как

где ${{N}_{1}} \geqslant 1$, ${{N}_{2}} \geqslant {{N}_{1}}$, $1 \leqslant {{N}_{u}} \leqslant {{N}_{2}}$, λ – это положительный весовой коэффициент, $e\left( {k + \frac{j}{k}} \right)$ = $\hat {y}\left( {k + \frac{j}{k}} \right)$ – $r\left( {k + \frac{j}{k}} \right)$ это ошибка предсказания, $\hat {y}\left( {k + \frac{j}{k}} \right)$ – это прогнозируемое выходное значение системы и $r\left( {k + \frac{j}{k}} \right)$ – это требуемое значение выхода системы [7].

С помощью модификации стандартного блока нелинейной модели Matlab/Simulink (Nonlinear ARX Model) можно получить модель авторегрессивного интегрального скользящего среднего (или модель Бокса–Дженкинса), которую можно использовать в формировании алгоритма управления, эта функция представлена в формуле (3) [12, 13]

где, $A({{q}^{{ - 1}}})$, $B({{q}^{{ - 1}}})$, $C({{q}^{{ - 1}}})$ являются многочленами оператора задержки q^–1

В уравнении (3) ${{\xi }}\left( k \right)$ – белый шум с нулевым средним и Δ = 1 – q^–1.

Для проверки разработанного алгоритма управления разработана имитационная модель [8, 13]. Параметрами имитационной модели гидросистемы являются: M_1max = = 4900 Нм; h_1max = 6 м; S = 7.07 м²; S₁ = 0.0314 м²; R = 1.5 м; S₂ = 0.0314 м²; ρ = 1000 кг/м³.

Для расчета параметров линеаризованной модели использовался метод наименьших квадратов, который соответствует фактическому значению выходной функции h₂(t). Таким образом, можно получить полиномы A(q^–1) и B(q^–1) дискретной модели авторегрессивнного интегрального скользящего среднего (6). Порядок расположения полиномов дискретной модели принимается na = 2, nb = 2 и nc = 0.

Ограничения для значения контрольного сигнала принимаются в соответствии с областью допустимых значений ${{u}_{1}}(t) \in \left[ {0,1} \right]$, ${{h}_{2}}(t) \in \left[ {0,3} \right]$. Весовые коэффициенты значения управляющего сигнала Δu(t) – λ = 0.1.

На выходе системы возникают помехи в виде белого шума, имитирующие погрешность измерения. Также на систему действуют величины M_Z1 и M_Z2. Значение M_Z1 = = 500 Нм в период времени 2500–3500 с. Значение M_Z2 = 200 Нм в период времени 6500–7500 с.

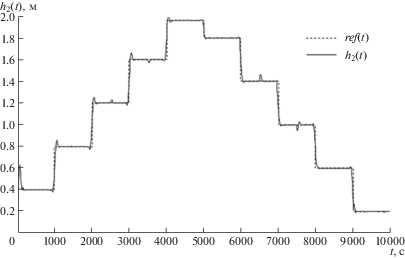
Результат ref(t) – целевое значение зависимости изменения высоты h₂ от времени и выходной функции системы h₂(t) с использованием алгоритма управления приведен на рис. 2.

Далее представим подход к формированию функции управления на основе нейронной модели. Рассмотрим алгоритм управления нелинейной системой (гидравлическая система подрессоривания, состоящая из двух резервуаров). Система состоит из управляемой нелинейной гидравлической системы, описываемой уравнениями (1), нейронной модели и управляющего контроллера. Поскольку алгоритму управления требуются параметры линейной модели динамической системы, в настоящей статье проводится расчет матрицы весовых коэффициентов динамической модели. Параметры и критерии оптимизации контроллера определяются функцией минимизации изменения высоты в резервуаре от целевого значения высоты (2) [7, 14, 15].

Выходом системы является уровень воды во втором резервуаре y(t) = h₂(t). Рассматривается модель нейронной системы с четырьмя входами и шестью нейронами в скрытом слое. Функции активации в скрытом слое являются тангентсальными (гиперболический тангенс, определяемый функцией $f(x)$ = $\operatorname{th} x$ = $\frac{2}{{1 + {{e}^{{ - 2x}}}}}$ – 1) функциями, а в выходном слое выбрана линейная функция [15, 16].

Представим результаты оценки (оценка производилась по критерию минимизации расхождений между целевым значением функции и фактическим, полученным в результате моделирования) параметров системы из автономной обучаемой нейронной модели и их применение в алгоритме управления для нелинейной системы взаимодействия двух резервуаров (1).

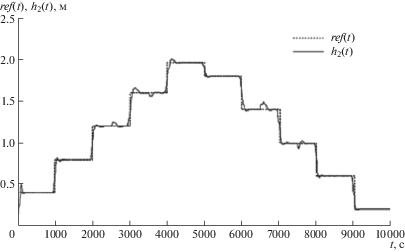
Результаты использования обучаемой нейронной модели показаны на рис. 3. На графике (рис. 3) сравниваются целевой выход системы h_2ref(t) и фактический выход системы h₂(t).

Заключение. На основании изложенного можно утверждать следующее. Если математическая модель динамической системы неизвестна, то целесообразно использовать подход, основанный на нейронной модели. В настоящей статье нейронная модель обучена как одноступенчатый перцептрон, соответствующий нелинейной системе. После обучения такую модель можно использовать для on-line оценки параметров системы. Полученные параметры системы были использованы для решения задачи оптимизации алгоритма управления. В противном случае (если математическая модель динамической системы известна), более эффективна будет работа классической модели формирования управляющего сигнала.