Проблемы машиностроения и надежности машин, 2022, № 1, стр. 13-25

Роботы различного назначения получили широкое распространение при выполнении основных и вспомогательных операций, перемещении заготовок и инструмента по заданной траектории с требуемой скоростью и точностью позиционирования. Роботизация является одним из основных факторов развития промышленности [1, 2].

Наиболее распространенные в настоящее время методики проектирования и исследования робототехнических комплексов ориентированы на использование матричных уравнений и отличаются выбором локальных систем координат [3, 4]. Силовой расчет обычно выполняют с использованием метода кинетостатики [5, 6], который позволяет рассматривать подвижную систему как условно неподвижную, находящуюся в квазистатическом равновесии.

Такие методы приводят к большим объемам вычислений с частым повторением однотипных процедур, применению высокопроизводительных вычислительных устройств, использующих алгоритмы параллельной обработки данных в многопроцессорных системах. Широкое распространение получили пакеты прикладных программ для моделирования работы роботов [7, 8]. Из-за сложности математического аппарата и численных методов расчета трудно оценить влияние вспомогательных факторов на результаты динамического анализа механизмов.

Проблема обеспечения необходимой точности позиционирования, расчета силовых факторов в кинематических парах и опасных сечениях звеньев остается актуальной. Продолжается поиск методов, ориентированных на совершенствование применяемого математического аппарата, методики расчета кинетической энергии звеньев механизмов с переходом от численных методов анализа к аналитическим [9, 10].

Кинетическая энергия является обязательным и обычно основным компонентом движения абсолютно твердых тел. Это требует особой ответственности при выборе методов ее определения, например при динамическом анализе мобильных роботов и иных механизмов, сложность которых с развитием технического прогресса возрастает. Основанием для расчета является теорема Кенига [11, 12] о равенстве кинетической энергии материальной системы сумме энергии переносного поступательного движения вместе с центром масс С и энергии вращательного движения относительно координатных осей, движущихся вместе с центром масс

где m – масса твердого тела; ${{{v}}_{C}}$ – скорость центра масс; I_C – момент инерции тела относительно мгновенной оси вращения, проходящей через центр масс; ω – мгновенная угловая скорость вращения твердого тела. Вычисление момента инерции относительно мгновенной оси вращения, которая в общем случае подвижна и зависит от движения тела, представляет определенные сложности.

Целью работы является: получение точного уравнения для расчета кинетической энергии вращающихся твердых тел без определения положения мгновенной оси вращения для динамического анализа механизмов с развитой структурой, таких как роботы-манипуляторы.

Рассмотрим вращение тела в плоскости х–у относительно неподвижного полюса Р$\left( {{{\alpha }_{P}},{{\beta }_{P}}} \right)$ в пространстве переменных Лагранжа [13]. При обозначениях текущих координат ${{x}_{i}} \in (x,y,z)$ будем использовать для переменных Лагранжа ${{\alpha }_{p}} \in (\alpha ,\beta ,\gamma )$ начальные координаты частиц ${{\left. {{{\alpha }_{р}} = {{x}_{p}}} \right|}_{{t = 0}}}$. Исходное положение произвольной точки М$\left( {\alpha ,\beta } \right)$ определим углом наклона ${{({{\theta }_{z}})}_{0}}$ прямой РМ по отношению к оси х и расстоянием между точками |PM| = L = const

После поворота прямой РМ на угол $\Delta {{\theta }_{z}} = {{\theta }_{z}} - {{({{\theta }_{z}})}_{0}}$ координаты точки $M(x,y)$ можно определить по аналогичным соотношениям

Исключая из этих уравнений длину L и начальное значение угла ${{({{\theta }_{z}})}_{0}}$ с помощью уравнений (2), получаем систему уравнений движения

и соответствующие им скорости

Нижний индекс t при обозначении координат ${{x}_{{i,t}}}$ и углов поворота ${{\theta }_{{i,t}}}$ соответствует дифференцированию соответствующих функций по времени $d{{x}_{i}}{\text{/}}dt \equiv {{x}_{{i,t}}}$, $d{{\theta }_{i}}{\text{/}}dt \equiv {{\theta }_{{i,t}}}$.

Для плоскопараллельных движений в других плоскостях уравнения могут быть получены с помощью круговой подстановки:

– при вращении относительно оси х

– при вращении относительно оси у

Нижний индекс при обозначении угла поворота тела ${{\theta }_{i}}$ указывает направление оси вращения, проходящей через полюс Р параллельно осям системы координат наблюдателя, относительно которой происходит вращение тела. Уравнения (3)–(6) будут использованы как исходные для всех дальнейших преобразований.

Для пространственных движений системы типа (6) можно получить с помощью принципа суперпозиции [14], который позволяет рассматривать их как одновременную реализацию нескольких плоскопараллельных движений. Если переменные Эйлера и Лагранжа совпадают в исходном состоянии ${{x}_{i}}({{\alpha }_{p}},t = 0)$ = ${{\alpha }_{i}}$, совмещение движений сводится к замене переменных Лагранжа внешнего движения $x_{i}^{{ex}}$ = $x_{i}^{{ex}}({{\alpha }_{p}},t)$ на выражения для соответствующих переменных Эйлера внутреннего движения $x_{i}^{{in}}$ = = $x_{i}^{{in}}({{\alpha }_{p}},t)$. Уравнения совмещенного движения ${{x}_{i}} = {{x}_{i}}({{\alpha }_{p}},t)$ при последовательном или одновременном их протекании совпадают с уравнениями внешнего движения после замены переменных Лагранжа соответствующими уравнениями для переменных Эйлера внутреннего движения

Внешние и внутренние движения аналогичны переносным и относительным в классической механике, но отличаются обязательным использованием единой системы координат. Принцип допускает многократное его применение без нарушения правила геометрического сложения скоростей и ускорений совмещаемых движений в каждой точке и в каждый момент времени [14–16].

Например, чтобы получить уравнения движения с вращением относительно подвижного полюса, следует наложить на вращения (3)–(6) поступательное перемещение полюса Р

В результате первое слагаемое (лагранжева координата) в каждом из уравнений (3)–(6) заменяется на текущую (эйлерову) координату

Каждая система из трех уравнений соответствует движению с четырьмя степенями свободы: три поступательных перемещения (8) вдоль координатных осей полюса Р и поворот тела $\Delta {{\theta }_{i}}$ относительно соответствующей оси.

Кинетическая энергия при произвольном вращении твердого тела. Уравнений (3)–(9) достаточно для определения любых кинематических характеристик движения абсолютно твердых тел, в том числе кинетической энергии, которую по определению для тела с объемом V, плотностью ρ и массой m определяет интеграл [11, 12]

С учетом разной природы аргументов при описании движения в форме Лагранжа, в уравнении (10) и ниже для обозначения бесконечно малых приращений аргументов и функций в пространстве переменных Лагранжа использован оператор δ, в том числе при интегрировании по массе δm. Оператор d характеризует бесконечно малые изменения функций во времени, как использовано выше для компонент скорости $d{{x}_{i}}{\text{/}}dt \equiv {{x}_{{i,t}}}$.

Точное интегрирование уравнения (10) можно выполнить при плоскопараллельном движении с вращением относительно одной оси, например z, когда по всему объему тела ${{z}_{t}} = 0$. С учетом уравнений движения (9) преобразуем правую часть к виду

Для интегрирования во втором слагаемом воспользуемся понятием центра масс С(x_C, y_C) [11, 12]

координаты которого можно вынести за знак интеграла и вместо (11) записать

Оставшийся в правой части интеграл в механике твердого тела называют моментом инерции при вращательном движении тела, по аналогии с массой m при поступательном движении [11, 12]. Принимая во внимание особенности более общего случая движения, в настоящей статье будем его называть, по аналогии с терминологией теории упругости [15, 16], полярным моментом инерции, как более полно отражающим его геометрический смысл, при сохранении принятого в механике твердого тела обозначения J_P

В результате вместо (13) получаем

Положение центра масс зависит от конфигурации тела и определяется по уравнениям (12). Положение полюса можно выбрать произвольно. Если в качестве полюса выбрать центр масс, последнее слагаемое обращается в ноль и формула (15) принимает простейший вид

Уравнение (16) можно распространить на любое пространственное поступательное движение с вращением относительно одной оси, т.к. компонента z_t   для всех частиц тела одинакова

Результат можно записать в инвариантной форме для любой оси

что совпадает с уравнением (1), т.к. ось вращения совпадает с мгновенной.

Получить точную аналитическую зависимость кинетической энергии при пространственном движении твердого тела без определения положения мгновенной оси вращения позволяет представление интеграла (10) в виде суммы трех интегралов, в каждом из которых подынтегральные функции представляют сумму одноименных компонент скорости совмещаемых плоскопараллельных движений

где штрихами обозначены компоненты скорости от трех вращений: один штрих – относительно оси х, два штриха – относительно оси у, три штриха – относительно оси z. Это соответствует правилу геометрического сложения скоростей при совмещении движений, оно выполняется при используемом принципе суперпозиции (7) [14].

Для сокращения математических записей рассмотрим сначала вращение тела относительно трех координатных осей, проходящих через неподвижный полюс Р$\left( {{{\alpha }_{P}},{{\beta }_{P}},{{\gamma }_{P}}} \right)$ и к полученному результату добавим энергию поступательного движения тела вместе с полюсом (8), как это предусмотрено в теореме Кенига [11, 12].

Из уравнений (3)–(6) следует, что в каждом интеграле из уравнения (18) одно из слагаемых обращается в ноль

Для первого интеграла с компонентами скорости вдоль оси х с учетом уравнений (3)–(6) получаем (верхний индекс при обозначении $E_{k}^{i}$ показывает направление компоненты скорости в данном интеграле)

Так как угловые скорости ${{\theta }_{{i,t}}}$ одинаковы для всех частиц тела, их можно вынести за знак интеграла

Оставшиеся в правой части интегралы относятся к осевым ${{(I_{i}^{j})}_{P}}$ и центробежным ${{(I_{{ij}}^{{}})}_{P}}$ моментам инерции [15, 16]

Для большей определенности верхний индекс у осевых моментов инерции ${{\left( {I_{i}^{j}} \right)}_{P}}$ указывает направление нормали к соответствующей плоскости, которая совпадает с осью вращения, указанной индексом угловой скорости ${{\theta }_{{i,t}}}$ в рассматриваемом слагаемом. Для центробежных моментов инерции, у которых множителями являются две угловые скорости, верхний индекс отсутствует. Строчные нижние индексы при моментах инерции ${{\left( {{{I}_{{ij}}}} \right)}_{P}}$ в уравнениях (22) и далее указывают переменные в соответствующих подынтегральных функциях. Уравнение (21) принимает вид

Для двух других интегралов уравнения (19), преобразуя их с помощью уравнений (5) и (6) к виду (20), находим

Суммируя правые части уравнений (23)–(25), получаем

где

Сумма осевых моментов инерции (27) в первых трех слагаемых уравнения (26) определяет квадраты расстояний между проекциями точки и полюса в разных плоскостях. При вращении твердого тела они остаются, как это следует из уравнений движения (3)–(6), постоянными и получаемые в результате полярные моменты инерции не изменяются, например

При использовании общепринятых в механике твердого тела обозначений (14)

вместо (26) получаем

Верхний индекс у моментов инерции $J_{P}^{i}$ соответствует оси, относительно которой он должен быть определен. Нижний индекс указывает точку, через которую должна проходить ось вращения $i \in (x,y,z)$.

Уравнение (30) не содержит никаких ограничений и применимо для любых вариантов пространственного движения тел с произвольным вращением. Последние слагаемые с центробежными моментами инерции ${{\left( {{{I}_{{ij}}}} \right)}_{P}}$, в отличие от полярных моментов инерции $J_{P}^{i}$ в первых трех слагаемых, изменяются при вращении тела и влияют на значения кинетической энергии.

Чтобы оценить возможный диапазон изменения центробежных моментов инерции в уравнении (30), воспользуемся начальными значениями осевых и центробежных моментов инерции, которые остаются неизменными в процессе движения тела. Их значения следуют из уравнений (27), если текущие координаты ${{x}_{i}} \in (x,y,z)$ приравнять начальным ${{\alpha }_{p}} \in (\alpha ,\beta ,\gamma )$

Для нижних индексов в левой части уравнений (31)–(32) использованы переменные Лагранжа ${{\alpha }_{P}} \in \left( {\alpha ,\beta ,\gamma } \right)$, чтобы отличить моменты инерции в исходном состоянии от текущих (27).

Полярные моменты инерции (29) остаются неизменными при повороте тела. Используя уравнения движения (3)–(6), систему (27) для центробежных моментов инерции (I_ij)_Р преобразуем к виду

или, с учетом обозначений для начальных значений (31)–(32),

Полученные уравнения совпадают с известными соотношениям для изменения центробежных моментов инерции твердых тел при повороте осей координат [15, 16]. Следовательно, три последних слагаемых в уравнении (30) учитывают изменение центробежных моментов инерции относительно осей системы координат наблюдателя за счет поворота тела. На долю кинетической энергии, определяемую слагаемыми с центробежными моментами инерции (33), влияют особенности вращения относительно всех осей. Если вращение происходит относительно только двух осей, например у и z, уравнение (30) принимает вид

где за счет $\Delta {{\theta }_{x}}$ = 0 оставшийся центробежный момент ${{({{I}_{{yz}}})}_{P}}$ не изменяется при повороте тела, как и полярные моменты инерции (29),

Если вращение происходит относительно только одной оси, уравнение (30) преобразуется к виду (15) для неподвижного полюса (первое и третье слагаемые обращаются в ноль)

При вращении относительно трех осей следует использовать уравнение (30) с центробежными моментами (33).

Если совместить полюс Р с центром масс С, уравнение (30) принимает вид

где для полярных моментов инерции вместо (29) получаем

Для центробежных моментов вместо (33) справедливы уравнения

где вместо (31)–(32) для центральных моментов инерции в исходном состоянии имеем

Для расчета кинетической энергии с учетом поступательного движения центра масс уравнения (30) и (36), в соответствии с теоремой Кенига, преобразуются к виду

Полярные моменты инерции $J_{P}^{i}$ определяют уравнения (29) или (37), центробежные (I_ij)_Р – (33) или (38).

Пример применения уравнений. Рассмотрим применение полученных уравнений на примере робота-манипулятора с двумя вращательными и одной винтовой кинематическими парами для перемещения груза массой m [1, 6]. Структурная схема робота с тремя независимыми приводами и вращением звеньев относительно пересекающихся осей представлена на рис. 1.

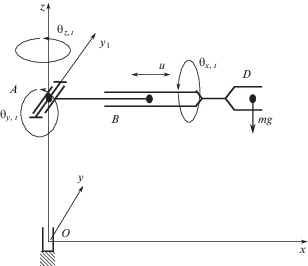
Звено 1 закреплено на стойке с помощью вращательной кинематической пары, которая позволяет звену вращаться относительно оси z, проходящей через начало координат. Частицы звена изменяют положение в пространстве наблюдателя в соответствии с уравнениями (3), которые с учетом принятой системы координат и положения полюса принимают вид

Звено 2 вращается относительно оси y₁, используя привод в кинематической паре с точкой А(α_А = 0, 0, γ_А = H)

Звенья 2 и 3 соединены винтовой кинематической парой в точке B(α_В = L₁, 0, γ_B = H). Привод обеспечивает поступательное и вращательное движения звена 3 относительно звена 2

Поступательное перемещение u определяет шаг винтовой пары h и угол поворота звена $\Delta {{\theta }_{x}}$

В соответствии с уравнением (7), для уравнений совмещенного движения звена 2 при внешнем движении звена 1 следует переменные Лагранжа в уравнениях (41) заменить соответствующими уравнениями (42)

Производные по времени определяют компоненты скорости частиц

Используя повторно правило суперпозиции (7), с учетом внутреннего движения (43) и внешнего (44) при равенстве координат ${{\beta }_{A}} = {{\beta }_{B}}$ и ${{\gamma }_{A}} = {{\gamma }_{B}}$ получаем для звена 3 вращение относительно трех осей

После дифференцирования по времени находим компоненты скорости, например, для (x_t)₃

Другие компоненты скорости для звена 3 не приведены для сокращения объема статьи. Правильность записи уравнений движения (44) и (46) можно проверить по условию отсутствия деформации [13]

Уравнения движения частиц переносимого груза в точке D зависят от особенностей его закрепления на звене 3. Для зажимных захватов уравнения совпадают с уравнением (46) для звена 3, но требуют конкретизации начальных координат рассматриваемой точки, например, для определения координат центра массы груза С_m(α_Cm, β_Cm, γ_Cm).

Зная компоненты скорости (45) и (47), кинетическую энергию звеньев можно найти численными способами [4–6], однако удобнее воспользоваться аналитическими зависимостями (39)–(40). Частицы звена 1 совершают плоскопараллельное движение, кинетическую энергию звена определяет уравнение (35). Частицы звена 2 вращаются относительно двух осей ${{\theta }_{{y,t}}} \ne \;{{\theta }_{{z,t}}} \ne 0$, ${{\theta }_{{x,t}}} = 0$, кинетическую энергию определяет уравнение (34). Звено 3 с подвижным полюсом В вращается относительно трех осей, кинетическую энергию определяет уравнения (39) или (40).

Для расчета требуемой мощности приводов и сил в кинематических парах целесообразно использовать анализ энергетических потоков, как в рычажных механизмах с замкнутыми кинематическими цепями [17]. Сумма скоростей изменения кинетической W_k = dE_k/dt и потенциальной W_p = dE_p/dt энергии движущихся тел на рассматриваемом участке механизма должна быть равна мощности W_e, поступающей от внешних источников

Выбор полюса в уравнении (46) однозначно определен на этапе кинематического анализа, т.к. уравнения (3)–(6) предполагают его движение известным. Он должен принадлежать кинематическим парам, соединяющим ведомое и ведущее звенья. Однако при расчете обобщенных сил удобнее использовать уравнение (40) с кинематическими характеристиками центра масс [17]. Например, для звена 3 требуемую мощность внешних сил определяет уравнение

где

Это наиболее громоздкая формула для динамического анализа рассматриваемого робота, но при ее использовании трудоемкость расчета существенно ниже по сравнению с матричными вариантами. Такая методика обеспечивает выполнение закона сохранения энергии на любой части механизма в любой момент времени.

Заключение. Уравнения (39) и (40) определяют кинетическую энергию твердого тела в самом общем случае пространственного движения с произвольным вращением относительно любых осей, не требуют определения положения мгновенной оси вращения и их можно использовать для динамического анализа механизмов любой сложности при известной информации о геометрических особенностях звеньев, позволяющих определить осевые, полярные и центробежные моменты инерции, а также о текущих значениях линейных и угловых скоростей [17].

Принимая во внимание, что осевые ${{\left( {I_{i}^{j}} \right)}_{P}}$ и центробежные ${{\left( {{{I}_{{ij}}}} \right)}_{P}}$ моменты инерции для исходного состояния тела (31)–(32) при движении не изменяются, можно утверждать, что текущие значения центробежных моментов (38) в зависимости от угла поворота тела $\Delta {{\theta }_{i}}$ изменяются по модулю, например для момента инерции ${{\left( {{{I}_{{xy}}}} \right)}_{С}}$ от исходного значения ${{\left( {{{I}_{{\alpha \beta }}}} \right)}_{С}}$ до половины разности осевых моментов инерции (в исходном состоянии) $[{{(I_{\alpha }^{z})}_{С}} - {{(I_{\beta }^{z})}_{С}}]{\text{/}}2$.

Для тел с равными главными моментами инерции, например для шара, когда ${{({{I}_{\alpha }})}_{С}} = {{({{I}_{\beta }})}_{С}} = {{({{I}_{\gamma }})}_{С}}$ и любые две ортогональные оси, проходящие через центр тяжести, являются главными центральными осями инерции, кинетическая энергия при неизменных угловых скоростях не изменяется. В противном случае первые слагаемые в уравнениях (38) за счет разности главных центральных моментов инерции приведут к циклическим изменениям кинетической энергии, возможному проявлению прецессии и нутации, амплитуда которых зависит от угловых скоростей вращения тела.

Структура полученных уравнений не позволяет предложить альтернативную методику аналитического определения момента инерции относительно мгновенной оси вращения J_C в уравнении (1). Момент инерции можно определить только экспериментально [11].