1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 1, 2022

Проблемы машиностроения и надежности машин, 2022, № 1, стр. 86-95

Разработка методики определения конструктивных параметров плетеных сетчатых конструкций авиакосмического назначения

С. А. Самипур 1, *, В. В. Батраков 2

1 Университет имени Шахида Бехешти
Тегеран, Иран

2 Казанский национальный исследовательский технологический университет им. А.Н. Туполева – КАИ
Казань, Россия

* E-mail: s_samipour@sbu.ac.ir

Поступила в редакцию 30.08.2021
После доработки 08.10.2021
Принята к публикации 20.10.2021

Полный текст (PDF)

Аннотация

В статье обсуждается аналитический расчет свойств жесткости плетеной сетчатой структуры для достижения двух целей. Первая – получить исходные данные для дальнейших расчетов с использованием МКЭ; вторая – предварительный выбор параметров плетеной сетчатой конструкции. Для достижения этих целей разработаны аналитические модели. Модели будут анализировать микроструктурное поведение плетеных композитов для оценки их механических свойств. Таким образом, модели можно проверить на экспериментальных данных. Этот подход основан на первичном предположении о периодическом распределении волокон в композите в двух масштабах, чтобы связать механические свойства композита с отдельными фазами. Первая шкала относится к ровнице, который представляет собой однонаправленный армированный волокном композит. Мы определяем механические свойства ровницы в этом масштабе. Вторая шкала относится к единичной ячейке в оплетке, поэтому окончательные механические свойства композита получаются в этой шкале. Далее описаны микромеханические и мезомеханические модели. Эти модели разработаны для анализа плетеных композитов и определения механических свойств зон переплетения сетчатых конструкций.

Ключевые слова: аэрокосмическая конструкция, композиционный материал, сетчатая структура, радиальное плетение

В работах многих авторов, в том числе С.В. Ломова [1] подробно разработаны экспериментальные и теоретические исследования моделирования плетеных композитов. Механические свойства плетеных композитов сильно зависят от геометрии плетения. Кривизна ровницы влияет на ударопрочность, жесткость и стабильность размеров композитных плетеных конструкций [2]. Микромеханическое моделирование необходимо для описания процесса разрушения из-за существеннoй взаимосвязи между геометрией переплетения, жесткостью, прочностью и поглощением энергии при ударе [3]. Ф.Т. Пирс [4] предложил простую модель, в которой ровницы имеют круглое поперечное сечение. В работе [5] разработано геометрическое описание, более подходящее для плетеных конструкций. L. Chen и др. [6] рассчитали эффективные упругие свойства трехмерных плетеных композитов с использованием метода конечных многофазных элементов. J.L. Li и др. [7] предложили геометрическую модель структуры волокна в современных композитах и сравнили поведение при сжатии, растяжении и изгибе. R.K. Gideon и др. [8] проверили поведение композитных труб с трехмерной оплеткой на осевое сжатие с различными углами оплетки. Z.Y. Tian и др. [9] теоретически исследовали механизм разрушения трехмерных плетеных композитов при двухосном растяжении и сжимающей нагрузке. H.L. Wang и др. [10] показали влияние температуры и угла плетения на повреждение при продольном сжатии. G.D. Fang и др. [11] использовали многомасштабный метод плетения для изучения поведения прогрессирующего повреждения трехмерных плетеных композитов.

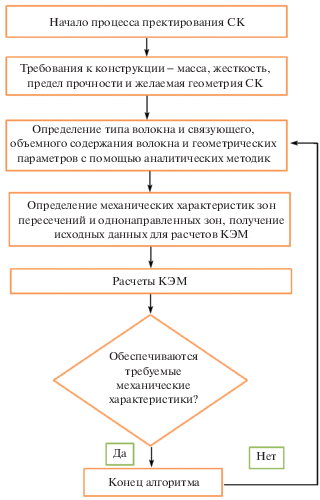
На рис. 1 представлен алгоритм определения расчетных параметров сетчатой структуры. Подходы к намотанной и плетеной конструкциям различаются из-за областей переплетения: в плетеных структурах ровницы заплетены (рис. 2а), а в намотанных – наложены друг на друга (рис. 3б, в).

Рис. 1.

Алгоритм определения конструктивных параметров СК.

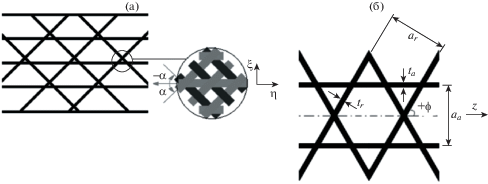
Рис. 2.

Зона переплетения трех ровниц СК: (а) – при плетении; (б), (в) – при намотке; уровни масштабирования: (г) – мезо-; (д) – микроуровень; микроскопические изображения структуры СК с объемным содержанием волокон: (е) – 54%; (ж) – 57%; (з) – параметры единичной ячейки; (и) – центральная линия ровницы.

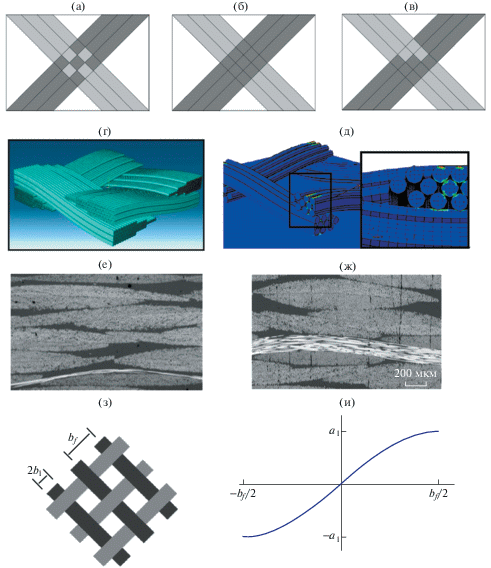
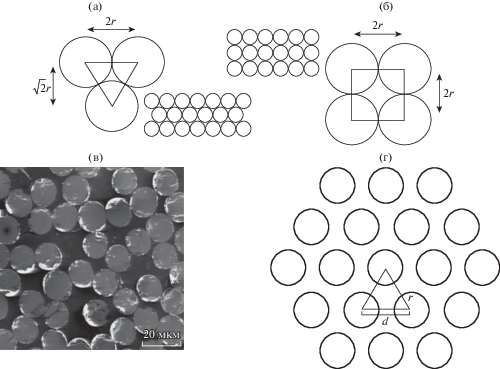
Рис. 3.

Расположение волокна в ровнице: (а) – по “треугольнику”; (б) – по “квадрату”; (в) – поперечное сечение волокон КМ; (г) – идеализированная модель.

Предварительно сформированная сетчатая конструкция производится путем регулярного переплетения двух групп ровниц: тех, которые всегда остаются прямыми при прохождении над другими ровницами или под ними, и тех, которые изгибаются при переходе от верхней к нижней части других ровниц. Это верно лишь отчасти для полотняного переплетения, когда ровницы согнуты по длине. Кривизна ровницы – основная причина, по которой плетеный композит имеет более низкие механические свойства, чем однонаправленный. Геометрию плетения можно идеализировать с помощью полиномиальных функций: эллиптической [12], дуги [13], синуса [14].

Во-первых, необходимо описать поперечное сечение, чтобы разработать аналитическую модель. Поперечное сечение ровниц зависит от объемной доли волокна и является линзовидным или уплощенным [15–17]. В нашем случае ровницы имеют одинаковые механические свойства и геометрию. Для получения гибридных композитов можно комбинировать различные свойства и материалы. Геометрию ровницы можно определить или оценить на основании изображений оптического микроскопа (рис. 2е–ж).

Рассматривается моделирование плетеной композитной единичной ячейки (ЭЯ) и моделирование отдельных ровниц, чтобы определить механические свойства СК и объемную долю волокна. Для построения полной геометрической модели ровницы используется синусоидальная функция [18]. Элементарная ячейка двухосной тканой заготовки показана на рис. 2з.

Уравнение $y(x) = A\sin (Bx)$ описывает ось ровницы в плетеной преформе, где А и В постоянны и определяются соответствующими граничными условиями. Таким образом, его можно вычислить при следующих граничных условиях:

(1)
$\begin{gathered} y(x)\left| {_{{x = - \frac{{{{b}_{f}}}}{2}}}} \right. = - {{a}_{1}};\quad y(x)\left| {_{{x = \frac{{{{b}_{f}}}}{2}}}} \right. = {{a}_{1}};\quad \frac{{\partial y(x)}}{{\partial x}}\left| {_{{x = - \frac{{{{b}_{f}}}}{2}}}} \right. = \frac{{\partial y(x)}}{{\partial x}}\left| {_{{x = \frac{{{{b}_{f}}}}{2}}}} \right. = 0; \\ y(x) = {{a}_{1}}\sin \left( {\frac{\pi }{{{{b}_{f}}}}x} \right), \\ \end{gathered} $
где ${{b}_{f}}$ – расстояние между центрами ровниц; ${{а}_{1}}$ – малая полуось поперечного сечения ровницы. Геометрию ровницы можно легко определить на рис. 2и.

Объемное содержание волокна в КМ – это отношение объема арматуры на элементарную ячейку к ее общему объему, которое определяется по формуле

(2)
${{{v}}_{f}} = \frac{{4{{b}_{1}}}}{{\pi {{b}_{f}}}}\sqrt {{{{({{a}_{1}})}}^{2}} + {{{(\varphi )}}^{2}}} \xi \left( {\frac{\pi }{{{{b}_{f}}}}|\frac{1}{{1 + {{{\left( {\frac{\varphi }{{{{a}_{1}}}}} \right)}}^{2}}}}} \right){{{v}}_{{{\text{fiber}}}}},$
где $\varphi = \frac{{{{b}_{f}}}}{{\pi \cos \alpha }}$; $\xi $ – эллиптический интеграл второго рода; ${{b}_{1}}$ – большая полуось поперечного профиля ровницы; $\alpha $ – угол армирования; ${{{v}}_{{{\text{fiber}}}}}$ – объемное содержание волокна в ровнице.

Определяется максимально возможная объемная доля волокна в монослое с помощью уравнения (2). При больших давлениях ровничные волокна могут быть распределены в виде треугольника (рис. 3а), тогда пустоты занимают только 9.31% ровницы. С учетом мезоструктур наибольшая объемная доля волокна в однослойном композите является

(2.3)
${{{v}}_{f}} = \frac{2}{\pi }\left( {1 - \frac{\pi }{{2\sqrt 3 }}} \right) = 57.73\% .$

Таким образом, это конечная объемная доля волокна, т.е. теоретически сложно добиться объемной доли волокна выше 57.73% в области переплетения.

Микроструктурное моделирование базируется на том, что, во-первых, поперечное сечение волокон является круговым, а во-вторых – схема расположения волокон не всегда является “треугольником” и “квадратом” (рис. 3в), поэтому предложена симметричная модель (рис. 3г).

В уравнении (2) ${{{v}}_{{{\text{fiber}}}}}$ – неустановленный параметр. Объемная доля волокна в ровнице формируется как соотношение объема волокна к общему объему ровницы. Применяя известные свойства ровницы, K – количество волокон в ровнице, объемную долю волокна можно рассчитать как

(4)
${{{v}}_{{{\text{fiber}}}}} = K\frac{{{{\pi }^{2}}}}{8}\frac{{r_{f}^{2}}}{{{{a}_{1}}{{b}_{1}}}},$
где rf – радиус волокна. Затем определяется объемная доля волокон в ровнице, чтобы определить расстояние между волокнами
(5)
${{{v}}_{{{\text{fiber}}}}} = \frac{{\frac{\pi }{2}r_{f}^{2}}}{{\frac{{\sqrt 3 }}{4}{{d}^{2}}}} = 3.6276{{\left( {\frac{{{{r}_{f}}}}{d}} \right)}^{2}},$
где d – расстояние между центрами волокон.

Уравнения (4) и (5) использованы для определения межосевого расстояния волокна в идеализированной модели ровницы: $d = {\text{1}}{\text{.7148}}\sqrt {\frac{{{{a}_{1}}{{b}_{1}}}}{K}} $.

Есть два способа получить исходные данные, поскольку волокна расположены в ровнице случайным образом, а поперечное сечение ровницы зависит от объемной доли волокна: 1) с использованием составных изображений микроструктуры; 2) расчетным путем с учетом того, что 50% волокон имеют “треугольное” расположение, а 50% волокон имеют “квадратное” расположение в ровнице. Тогда с помощью уравнения (5): ${{{v}}_{{{\text{fiber}}}}} = 0.846$.

Далее расстояние между центрами волокон устанавливают по уравнению (5). Затем определяются размеры идеализированной волоконной модели и модули упругости однонаправленного композита с использованием комбинированной модели и плетеного композита.

В качестве примера возьмем комбинацию углеродного волокна T700S и смолы T–26. Их механические свойства приведены в таблице 1.

Таблица 1
Параметры Волокно T700S Смола T–26
Модуль Юнга, ГПа 230 3.1
Плотность, кг/м3 1800 1170

Взаимозависимость продольных и поперечных модулей упругости композита для однонаправленного строения от параметра ${{{v}}_{{{\text{fiber}}}}}$: ${{{v}}_{{{\text{fiber}}}}}$ – 0.7; E1, ГПа – 162; E2, ГПа – 7.4.

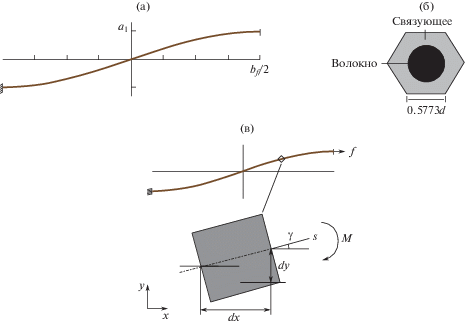
На рис. 4а представлена модель волокна, состоящего из одного волокна и смолы вокруг него. Используется энергетический метод для определения перемещения: ${{X}_{1}}$ = = $\int_0^l {\frac{M}{{EI}}\frac{{\partial M}}{{\partial f}}dx} $, где I – момент инерции сечения консольной балки; $E$ – модуль упругости;  f – сила, действующая на консольной балке; M – изгибающий момент (рис. 4в).

Рис. 4.

Волоконная модель: (а) – идеализированная волоконная модель; (б) – ее поперечное сечение; (в) – сила и изгиб, действующий на модель волокна.

Перемещения относительно осей x и y определим как

${{\delta }_{x}} = \int\limits_{ - \frac{{{{b}_{f}}}}{2}}^{\frac{{{{b}_{f}}}}{2}} {\frac{M}{{EI}}\frac{{\partial M}}{{\partial f}}} \sin (\gamma )dx;\quad {{\delta }_{y}} = \int\limits_{ - \frac{{{{b}_{f}}}}{2}}^{\frac{{{{b}_{f}}}}{2}} {\frac{M}{{EI}}\frac{{\partial M}}{{\partial f}}} \cos (\gamma )dx,$
где $M = f({{a}_{1}} - y)$; $y = {{a}_{1}}\sin \left( {\frac{\pi }{{{{b}_{f}}}}x} \right)$; $I = 0.06a_{t}^{4}$ – момент инерции; где at – размер шестиугольника; $\gamma = \operatorname{arctg} \left( {\frac{{\partial y}}{{\partial x}}} \right)$ = $\operatorname{arctg} \left( {\frac{{{{a}_{1}}\pi }}{{{{b}_{f}}}}\cos \left( {\frac{\pi }{{{{b}_{f}}}}x} \right)} \right)$.

Перемещение под действием аксиальной силы определяется как

${{\Delta }_{x}} = \int\limits_{ - \frac{{{{b}_{f}}}}{2}}^{\frac{{{{b}_{f}}}}{2}} {\frac{{f\cos ({{\gamma }})}}{{AE}}\cos ({{\gamma }})dx} ;\quad {{\Delta }_{y}} = \int\limits_{ - \frac{{{{b}_{f}}}}{2}}^{\frac{{{{b}_{f}}}}{2}} {\frac{{f\cos ({{\gamma }})}}{{AE}}} \sin ({{\gamma }})dx.$

Модуль упругости модели изогнутого волокна определяется выражением

(6)
$\begin{gathered} {{E}_{x}} = \frac{{{{{{\sigma }}}_{x}}}}{{{{{{\varepsilon }}}_{x}}}} = \frac{{f{\text{/}}A}}{{({{{{\delta }}}_{x}} + {{\Delta }_{x}}){\text{/}}l}} = \frac{{fl}}{{({{{{\delta }}}_{x}} + {{\Delta }_{x}})A}}, \\ {{E}_{x}} = \frac{{fl}}{{A\int\limits_{ - \frac{{{{b}_{f}}}}{2}}^{\frac{{{{b}_{f}}}}{2}} {\left( {\frac{M}{{EI}}\frac{{\partial M}}{{\partial f}}\sin ({{\gamma }}) + \frac{{f\cos ({{\gamma }})}}{{AE}}\cos ({{\gamma }})} \right)dx} }}. \\ \end{gathered} $

Таким образом, разработана аналитическая модель для определения модуля упругости плетеного композита. Это дает возможность определять упругие свойства областей переплетения сетчатых конструкций.

Рассмотрим аналитический метод определения модуля упругости единичной ячейки сетчатых конструкций с плетеной арматурой.

Модули упругости по осям для двухосного плетения ${{\eta }}$ и ${{\xi }}$ выражают как

${{E}_{{{\eta }}}} = E_{{{\eta }}}^{f}{{{v}}_{f}} + (1 - {{{v}}_{f}}){{E}_{m}};\quad {{E}_{{{\xi }}}} = E_{{{\xi }}}^{f}{{{v}}_{f}} + (1 - {{{v}}_{f}}){{E}_{m}},$
где $E_{{{\eta }}}^{f}$, $E_{{{\xi }}}^{f}$ – модули упругости плетеного КМ по осям ${{\eta }}$ и ${{\xi }}$, которые получаются следующим образом [16]:
$\begin{gathered} \frac{1}{{E_{\eta }^{f}}} = \frac{{{{{\cos }}^{4}}\alpha }}{{{{E}_{1}}}} + \frac{{{{{\sin }}^{4}}\alpha }}{{{{E}_{2}}}} + \left( {\frac{1}{{{{G}_{{12}}}}} - \frac{{{{{v}}_{{12}}}}}{{{{E}_{1}}}}} \right){{\cos }^{2}}\alpha {{\sin }^{2}}\alpha ; \\ \frac{1}{{E_{\xi }^{f}}} = \frac{{{{{\sin }}^{4}}\alpha }}{{{{E}_{1}}}} + \frac{{{{{\cos }}^{4}}\alpha }}{{{{E}_{2}}}} + \left( {\frac{1}{{{{G}_{{12}}}}} - \frac{{{{{v}}_{{12}}}}}{{{{E}_{2}}}}} \right){{\sin }^{2}}\alpha {{\cos }^{2}}\alpha , \\ \end{gathered} $
где ${{E}_{1}}$, ${{E}_{2}}$ – представляют собой аксиальный и нормальный модули упругости тканого композита, установленные по формуле (5); ${{G}_{{12}}}$ – модуль сдвига; ${{{v}}_{{12}}}$ – коэффициент Пуассона.

Модули упругости для трехосного плетения по осям ${{\eta }}$ и ${{\xi }}$ находим как

(7)
$\begin{gathered} {{E}_{\eta }} = E_{\eta }^{f}{{{v}}_{f}} + \left( {1 - {{{v}}_{f}}} \right){{E}_{m}} = E_{{{{\eta }_{1}}}}^{f}{{{v}}_{{{{f}_{1}}}}} + E_{{{{\eta }_{2}}}}^{f}{{{v}}_{{{{f}_{2}}}}} + E_{{{{\eta }_{3}}}}^{f}{{{v}}_{{{{f}_{3}}}}} + \left( {1 - {{{v}}_{f}}} \right){{E}_{m}}, \\ {{E}_{\xi }} = E_{\xi }^{f}{{{v}}_{f}} + \left( {1 - {{{v}}_{f}}} \right){{E}_{m}} = E_{{{{\xi }_{1}}}}^{f}{{{v}}_{{{{f}_{1}}}}} + E_{{{{\xi }_{2}}}}^{f}{{{v}}_{{{{f}_{2}}}}} + E_{{{{\xi }_{3}}}}^{f}{{{v}}_{{{{f}_{3}}}}} + \left( {1 - {{{v}}_{f}}} \right){{E}_{m}}, \\ \end{gathered} $
где $E_{{{{{{\eta }}}_{1}}}}^{f}$, $E_{{{{{{\eta }}}_{3}}}}^{f}$ и $E_{{{{{{\xi }}}_{1}}}}^{f}$, $E_{{{{{{\xi }}}_{3}}}}^{f}$ – модули упругости спиральных волокон по осям ${{\eta }}$ и ${{\xi }}$; $E_{{{{{{\eta }}}_{2}}}}^{f}$, $E_{{{{{{\xi }}}_{2}}}}^{f}$ – модули упругости продольных волокон по осям ${{\eta }}$ и ${{\xi }}$; ${{{v}}_{{{{f}_{2}}}}}$ – объемное содержание продольных волокон; ${{{v}}_{{{{f}_{1}}}}}$, ${{{v}}_{{{{f}_{3}}}}}$ – объемное содержание спиральных волокон. Спиральные волокна расположены под углом $\alpha $, поэтому:

$E_{{{{{{\eta }}}_{1}}}}^{f} = E_{{{{{{\eta }}}_{3}}}}^{f} = E_{{{\eta }}}^{f};\quad E_{{{{{{\eta }}}_{2}}}}^{f} = {{E}_{1}}.$

Как показано в табл. 2, результаты аналитического расчета модуля упругости ЕТ продемонстрировали высокую сходимость с результатами численных и экспериментальных исследований ЕВ, выполненных другими авторами. Все расчеты производились в MATLAB.

Таблица 2
Источник Волокно Смола α ${{{v}}_{f}}$, % ${{E}_{B}}$, ГПа ${{E}_{T}}$, ГПа Err, %
[19] M46J RTM–6 0, ±15 40 152.90 156.18 4.11
[20] M46J RTM–6 0, ±45 55 91.99 93.65 1.81

Следовательно, на основании микромеханики была разработана аналитическая модель для вычисления упругих свойств композиционных сетчатых конструкций. Использование этой модели для микромеханического анализа однонаправленных областей и областей переплетения сетчатых конструкций, можно определить упругие свойства плетеных композитов на основе волокна, смолы и угла плетения.

Здесь предлагается метод выбора конструктивных параметров СК. Вводится система уравнений для описания веса, геометрии и механических свойств плетеного СК: уравнение массы, уравнение геометрии и уравнение упругих свойств. Рис. 5 демонстрирует геометрию СК. Масса конструкции определяется как

(8)
${{m}_{s}} = 2\frac{L}{{\cos \phi }}{{t}_{r}}{{h}_{r}}{{\rho }_{m}}\frac{L}{{{{a}_{r}}}}\sin \phi + 2\pi rL{{\rho }_{m}}\frac{{{{t}_{a}}}}{{{{a}_{a}}}}{{h}_{a}} = 2\pi rL{{\rho }_{m}}\left( {2\frac{{{{t}_{r}}{{h}_{r}}}}{{{{a}_{r}}}} + \frac{{{{t}_{a}}{{h}_{a}}}}{{{{a}_{a}}}}} \right),$
где L, r – длина и радиус конструкции, соответственно; $\phi $ – угол между спиральными и продольными ребрами; ${{t}_{{r(a)}}}$, ${{h}_{{r(a)}}}$, ${{a}_{{r(a)}}}$ – ширина, толщина и расстояние между спиральными и продольными ребрами, соответственно.

Рис. 5.

(а) – Фрагмент СК с продольными ребрами; (б) – геометрические параметры СК.

Уравнение массы конструкции является целевой функцией, т.е. цель состоит в том, чтобы минимизировать вес конструкции с учетом геометрии и механических свойств. На рис. 6а показана структура с областями переплетения с двойным и тройным перекрытием ровницы в схеме трехосного плетения. На рис. 6б показана структура с областями переплетения в схеме двухосного плетения. Отличие состоит в том, что толщина областей переплетения в конструкции с тройным перекрытием ровницы в три раза больше толщины областей с однонаправленным материалом, что приводит к более значительному изгибу ровниц. Эта особенность плетеной структуры снижает механические свойства композита, поэтому это необходимо учитывать в процессе проектирования.

Рис. 6.

Схема зон переплетений СК: (а) – зоны тройного наложения; (б) – зоны двойного наложения.

Для определения геометрии СК без областей переплетения с тройным перекрытием ровниц установим неравенство

$\frac{1}{2}\frac{{{{a}_{r}}}}{{\cos \phi }} \geqslant \left( {{{t}_{a}} + \frac{{{{t}_{r}}}}{{\cos \phi }}} \right).$

При ${{a}_{r}} = 2({{t}_{a}}\cos \phi + {{t}_{r}})$ коэффициент покрытия получается как

(9)
$k = 1 - {{\left( {1 - \frac{{{{t}_{r}}}}{{{{a}_{r}}}}} \right)}^{2}} + {{\left( {\frac{{{{t}_{a}}}}{{{{a}_{r}}}}} \right)}^{2}}\frac{{2\sin 2\phi }}{{\operatorname{tg} \phi }}.$

Это наименьший коэффициент покрытия для сетчатых конструкций без областей трехосного переплетения. Для сетчатых структур устанавливается следующее неравенство: $0 < k < 1$.

Если расстояние между ребрами в na раз больше ширины ребер, то коэффициент покрытия определяется следующим образом: $k = 1 - {{\left( {1 - \frac{1}{{{{n}_{a}}}}} \right)}^{2}}$.

Таким образом, коэффициент покрытия может связывать механические свойства и технологические параметры производства трубчатых конструкций со сплошной стенкой со свойствами сетчатой структуры. Иными словами, конструкции с известным весом, но с различными коэффициентами покрытия, отличаются механическими свойствами, т.е. вес конструкции и конкретные механические свойства можно оптимизировать с использованием коэффициента покрытия.

Выводы. С помощью (3) определяется объемная доля волокна в зонах переплетения. Затем тип волокна и смолы, а также угол оплетки определяются на основании расчета упругих свойств СК с использованием (7) с учетом технологических свойств и требований к конструкции, таких как жесткость и размеры деталей. Начальные конструктивные параметры, такие как толщина, ширина и расстояние между спиральными ребрами, можно установить с помощью уравнений (8) и (9). Кроме того, эти параметры использованы в расчетах МКЭ.

Список литературы

  1. Lomov S.V., Nakai A., Parnas R.S., Bandyopadhyay S., Ghosh I. Verpoest Experimental and theoretical characterisation of the geometry of flat two- and three-axial braids // Textile Research Journal. 2002. V. 72. № 1. P. 706.

  2. Carey J., Fahim A., Munro M. Predicting elastic constants of 2D-braided fiber rigid and elastomeric-polymeric matrix composites // Journal of Reinforced Plastics and Composites. 2004. V. 23. P. 1845.

  3. Ayranci C., Carey J.P. Predicting the longitudinal elastic modulus of braided tubular composites using a curved unit-cell geometry // Composites Part B: Engineering. 2010. V. 41. P. 229.

  4. Pierce F.T. The geometry of cloth structure // Journal of Textile Inst. 1937. V. 28. P. 45.

  5. Carey J., Munro M., Fahim A. Regression-based model for elastic constants of 2D braided/woven open mesh angle-ply composites // Polymer Composites. 2005. V. 26. P. 152.

  6. Chen L., Tao X.M., Choy C.L. Mechanical analysis of 3-D braided composites by the finite multiphase element method Compos // Sci. Technol. 1999. V. 59. P. 2383.

  7. Li J.L., Jiao Y.N., Sun Y., Wei L.M. Experimental investigation of cut-edge effect on mechanical properties of three-dimensional braided composites // Materials & Design 2007. V. 28 (9). P. 2417.

  8. Gideon R.K., Zhou H.L., Li Y., Sun B.Z., Gu B.H. Quasi-static compression and compression-compression fatigue characteristics of 3D braided carbon/epoxy tube // J. Text. Inst. 2016. V. 107 (7). P. 938.

  9. Tian Z.Y., Yan Y., Li J., Hong Y., Guo F.L. Progressive damage and failure analysis of three-dimensional braided composites subjected to biaxial tension and compression // Composite Structures 2018. V. 185. P. 496.

  10. Wang H.L., Sun B.Z., Gu B.H. Numerical modeling on compressive behaviors of 3-D braided composites under high temperatures at microstructure level // Composite Structures 2017. V. 160. P. 925.

  11. Fang G.D., Liang J., Wang Y., Wang B.L. The effect of yarn distortion on the mechanical properties of 3D four-directional braided composites // Composites Part A: Applied Science and Manufacturing. 2009. V. 40 (4). P. 343

  12. Ayranci C., Carey J.P. Experimental validation of a regression-based predictive model for elastic constants of open mesh tubular diamond-braid composites // Polymer Composites. 2011. V. 32. P. 243.

  13. Fang G., Liang J.A. Review of numerical modeling of three-dimensional braided textile composites // Journal of Composite Materials. 2011. V. 45. P. 2415.

  14. Ivey M.A., Carey J.P.R., Ayranci C. Braid reinforced polymeric rebar production and characterization // Presented at International SAMPE Technical Conference, 2014.

  15. Vasiliev V.V., Rain A.F. Anisogrid Composite Lattice Structures for Spacecraft and Aircraft Applications // Composite Structures. 2006. V. 76. P. 182.

  16. Vasiliev V.V., Pichkhadze G.P. Composite shells and plates with spatial reinforcement // Design, analysis and testing of composite structures. 1982. V. 9. P. 83.

  17. Vasiliev V.V., Morozov E.V. Mechanics and analysis of composite materials // Elsevier, 2001.

  18. Vasiliev V.V., Lopatin A.V. Theory of lattice and stiffened composite shells // Mechanics of composite structures. Novosibirsk: Nauka, 1984. P. 31.

  19. Samipour S.A., Khaliulin V.I., Batrakov V.V. Development of the Technology of Manufacturing Aerospace Composite Tubular Elements by Radial Braiding // Journal of Machinery Manufacture and Reliability. 2018. V. 47 (3). P. 284.

  20. Samipour S.A., Khaliulin V.I., Batrakov V.V. Manufacturing Technology of Aerospace Braided Lattice Structures // Journal of Machinery Manufacture and Reliability. 2020. V. 49. № 9. P. 787.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал