Проблемы машиностроения и надежности машин, 2022, № 1, стр. 96-102

Современный этап развития науки и техники многие теоретики и практики связывают с широким использованием робототехнических систем и интеллектуальных процессов, миниатюризацией элементной базы изделий, интеграцией информационных систем, применением новых физических принципов.

Такая тенденция сопровождается значительным усложнением самых разнообразных по устройству и назначению технических систем, для исследования которых приходится прибегать к использованию моделей. Поэтому вопросы, связанные с идентификацией, являются весьма актуальными.

Идентификация представляет собой получение или уточнение математической модели исследуемой системы по ее измеряемым входным и выходным сигналам [1].

В зависимости от наличия априорной информации об исследуемой системе различают структурную, параметрическую и непараметрическую идентификацию (рис. 1) [2].

Структурная идентификация предполагает построение модели “черного ящика” с неизвестными структурой и параметрами системы. Поскольку структурная идентификация представляет собой сложную проблему, то в настоящее время по данному направлению отсутствуют четко формализованные методы ее решения. Вместе с тем, в аспекте проблематики структурной идентификации развиваются методы, основанные на свойстве сложности систем. Основная идея таких методов заключается в идентификации системы так, чтобы обеспечить ограниченную сложность ее модели при заданной точности [3].

Параметрическая идентификация предполагает построение модели “серого ящика” с известной структурой, но неизвестными параметрами. В основе этой модели лежат передаточные функции, а также алгебраические, дифференциальные или интегродифференциальные уравнения, которые функционально связывают входные и выходные сигналы системы. Наиболее известными методами параметрической идентификации являются: метод наименьших квадратов, метод апостериорной вероятности, метод стохастической аппроксимации, градиентные методы [1, 4–7].

Непараметрическая идентификация направлена на построение модели весовой (импульсной передаточной) функции. Построение такой модели представляет собой довольно трудоемкий процесс, включающий описание структуры модели идентифицируемой системы, решение уравнения идентификации, обработку результатов, получение оценок параметров модели, анализ этих оценок и проверку адекватности модели [1].

Важное место среди перечисленных этапов отводится решению уравнения непараметрической идентификации, которое при наличии по одному входному и выходному случайным сигналам в общем виде выглядит как

где τ – момент подачи входного x(t) сигнала относительно начала отсчета; K_yx(t) – взаимно-корреляционная функция входного x(t) и выходного y(t) сигналов; K_xx(t) – автокорреляционная функция входного x(t) сигнала; h(t) – неизвестная весовая функция, позволяющая при произвольной x(t) определять y(t).

Выражение (1) представляет собой частный вид интегрального уравнения Фредгольма первого рода

где λ – параметр; K(z, s) – ядро уравнения;  f(z) – свободный член уравнения; φ(s) – искомая функция.

В уравнении идентификации (1) λ = 1, искомой функцией является весовая функция h(t), а ядром – автокорреляционная функция K_xx(t) входного x(t) сигнала.

Для решения уравнения (1) можно использовать различные временные и частотные (спектральные) методы [8–13]. Вместе с тем, эти методы имеют ограниченные условия применения. Одни методы оказываются непригодными для идентификации динамических систем, входные и выходные сигналы которых имеют вероятностный характер. Другие методы требуют исчерпывающей информации о входных и выходных сигналах и существенных затрат вычислительных ресурсов.

В связи с этим предлагается оригинальный метод решения уравнения непараметрической идентификации динамической системы, который лишен указанных выше недостатков.

Рассмотрим применение метода на примере.

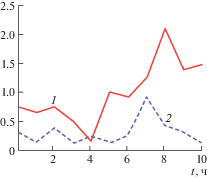
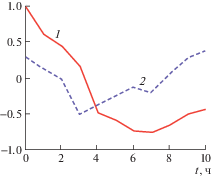
Пусть в течение десяти часов проведены измерения входного x(t) и выходного случайных сигналов y(t). Сигнал x(t) подчиняется нормальному закону распределения с математическим ожиданием m_x = 1 и среднеквадратичным отклонением σ_x = 0.5. В свою очередь, сигнал y(t) подчиняется показательному закону распределения с математическим ожиданием m_y = 2 (рис. 2).

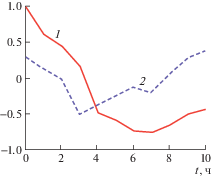
Вычислим автокорреляционную функцию K_xx(t) входного x(t) сигнала и взаимно-корреляционную функцию K_yx(t) входного x(t) и выходного y(t) сигналов (рис. 3).

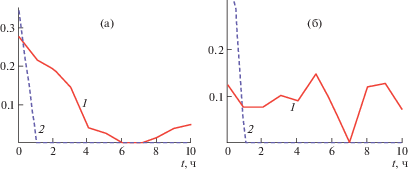
Перенесем функции K_xx(t) и K_yx(t) на положительную ось. Для этого сначала необходимо найти минимальные значения функций K_xx(t) и K_yx(t), а затем добавить их абсолютные значения к каждому значению функций. В результате получим функции $K_{{xx}}^{ + }(t)$ и $K_{{yx}}^{ + }(t)$, представленные на рис. 4.

Проведем нормирование функций $K_{{xx}}^{ + }(t)$ и $K_{{yx}}^{ + }(t)$, чтобы представить их в вероятностной форме. Для этого воспользуемся формулами:

где F_xx(t) и F_yx(t) – аналоги функций распределения.

Вычислим для F_xx(t) и F_yx(t) приближенное представление плотностей распределения на основе гипердельтной аппроксимации, которую можно применять для произвольных функций распределений [14].

Сущность гипердельтной аппроксимации заключается в представлении произвольной плотности распределения сосредоточенной на временной оси, приближенно в виде

где С_i – вероятности, удовлетворяющие условию $\sum\nolimits_{i = 1}^n {{{C}_{i}}} = 1$; T_i – постоянные параметры; δ – дельта-функция Дирака.

В случае n > 2, значения С_i и T_i определяются численно. Если n = 2, то

где ${{\nu }_{i}}$ – i-й начальный момент случайной величины, распределенной с плотностью вероятности  f(t).

Для приближенного представления по методу моментов воспользуемся тремя начальными моментами. В результате получим аппроксимированные плотности вероятностей распределения  f_Δxx(t) и  f_Δyx (t).

На основе плотностей вероятностей распределения f_Δxx(t) и f_Δyx(t) найдем их функции распределения

Графики получившихся аппроксимированных функций распределения F_Δxx(t) и F_Δyx(t) представлены на рис. 5.

Аппроксимированные функции F_Δxx(t) и F_Δyx(t), в отличие от F_xx(t) и F_yx(t), удовлетворяют условию Липшица–Гельдера всюду на оси t > 0 даже в точках, где имеются разрывы первого рода. Поэтому для F_Δxx(t) и F_Δyx(t) можно получить изображения Лапласа

Следовательно, уравнение (1), используя изображения Лапласа $F_{{\Delta xх}}^{*}(s)$, $F_{{\Delta ух}}^{*}(s)$ и $h{\kern 1pt} *{\kern 1pt} (s)$, можно представить как

где h*(s) – изображение Лапласа весовой функции h(τ).

Откуда $h{\kern 1pt} *{\kern 1pt} (s) = \frac{{F_{{\Delta yх}}^{*}(s)}}{{F_{{\Delta xх}}^{*}(s)}}$.

Для получения выражения весовой функции h(τ) во временной области необходимо применить обратное преобразование Лапласа. Однако достичь ожидаемых результатов достаточно затруднительно из-за сложности прямого изображения Лапласа искомой весовой функции и вычислительных трудностей. Поэтому переход от изображений h*(s) к оригиналу h(t) проведем, применяя приближенный способ обращения преобразования Лапласа с использованием формулы Алфрея. Эта формула вытекает из формулы Уайдера на основе свойства фильтрации преобразования Лапласа с помощью дельта-функции. Она имеет вид [15] $h(\tau ) \approx sh{\kern 1pt} *{\kern 1pt} (s)$ при $s = {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }$.

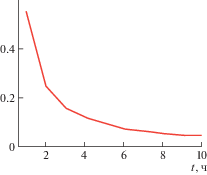
Полученная весовая функция является одномерной моделью системы, позволяющей определить реакцию системы на произвольное входное воздействие.

При заданных исходных данных график искомой весовой функции будет выглядеть так, как это показано на рис. 6.

Таким образом, разработанный метод позволяет определять весовую функцию динамической системы на основе гипердельтной аппроксимации автокорреляционной и взаимно-корреляционных функций входного и выходного случайных сигналов с произвольными законами распределения, а также преобразования Лапласа.

Применение рассмотренного метода обеспечит выполнение непараметрической идентификации динамических систем в условиях наличия ограничений на вычислительные ресурсы, а также проведение измерений входных и выходных сигналов.

Вместе с тем, вопрос оценки точности предлагаемого метода остается открытым и требует дальнейшего экспериментального исследования при идентификации технических систем, отличающихся устройством, функциональностью и назначением. Для повышения точности результатов количество начальных моментов для автокорреляционной и взаимно-корреляционных функций входного и выходного случайных сигналов может быть увеличено.

Дальнейшее направление развития метода можно связать с разработкой частных методик непараметрической идентификации многомерных систем различного назначения.