Проблемы машиностроения и надежности машин, 2022, № 2, стр. 3-12
Структурный и кинематический анализ рычажного вариатора с пространственными преобразующими механизмами
А. А. Абдираимов 1, Е. С. Гебель 2, *
1 Кыргызский государственный технический университет им. И. Раззакова
Бишкек, Кыргызская Республика
2 Омский государственный технический университет
Омск, Россия
* E-mail: Gebel_es@mail.ru
Поступила в редакцию 09.07.2021
После доработки 09.11.2021
Принята к публикации 20.12.2021
- EDN: EMLHMO
- DOI: 10.31857/S023571192202002X
Аннотация
В статье описаны схема и принцип работы рычажного вариатора с пространственными преобразующими механизмами. В результате структурного анализа, определено семейство исследуемого вариатора. Показано, что применение сферических кинематических пар оказывается предпочтительнее для надежности работы устройства. Предложена математическая модель кинематики рычажного вариатора с двумя преобразующими механизмами, и построены диаграммы изменения передаточного отношения в зависимости от угла поворота входного кривошипа и положения камня на неподвижной кулисе.
Большинство современных автомобилей оснащаются автоматическими коробками переключения передач, которые по сравнению с механической трансмиссией обеспечивают более комфортные условия вождения в городских условиях, а также экономию топлива и более плавную динамику разгона [1]. Одним из перспективных способов организации бесступенчатых трансмиссий являются вариаторы [2–4].
В настоящее время известны разнообразные типы вариаторов скоростей (фрикционные, тороидные, ременные, шаровые и т.д.) [5–8], главным недостатком которых является использование фрикционной передачи для передачи движения от ведущего колеса к ведомому. Это обстоятельство не позволяет получить точного передаточного отношения из-за проскальзывания, требует дополнительных устройств для прижатия колес, что приводит к повышению нагрузок на валы и подшипники.
Для избежания вышеуказанных недостатков применяются различные типы импульсных вариаторов [4, 9]. В импульсных вариаторах вращательное движение ведущего вала (кривошипа) преобразуется в колебательное движение, которое с помощью механизмов свободного хода (МСХ) вновь трансформируется во вращательное движение ведомого вала. В указанных вариаторах в качестве преобразующего механизма используются рычажные, зубчато-рычажные и кулачковые механизмы, а передаточные отношения изменяются посредством изменения радиуса (длины) вращения кривошипа-вращения или длины качания коромысла-качения [4, 9]. В импульсных вариаторах движение передается в виде периодических импульсов, чтобы получить непрерывное вращение ведомого вала и уменьшить неравномерность его вращения, устанавливают несколько последовательно работающих преобразующих механизмов и МСХ, причем эти механизмы устанавливаются через равные промежутки. Необходимость регулирования длины кривошипа или коромысла усложняет конструкцию импульсного вариатора.
Для плавного регулирования передаточного отношения в широком диапазоне используется вариатор с рычажными механизмами [10, 11], вращение ведущего кривошипа преобразуется в непрерывное вращательное движение шестерен. Бесступечатое регулирование передаточного отношения осуществляется путем изменения радиуса кривошипа или перемещением ползуна. К недостаткам образца [10] относят его низкую надежность, вследствие неравномерности вращения выходного вала при достижении входным валом крайних мертвых точек, что приводит к разрыву крутящего момента.
Для устранения таких недостатков и плавного регулирования передаточного отношения разработана конструкция рычажного вариатора с пространственными преобразующими механизмами (рис. 1) [12, 13]. В предложенном устройстве, как и в импульсных вариаторах, вращение кривошипа преобразуется в колебательное движение и с помощью МСХ трансформируется во вращательное движение ведомого кривошипа.
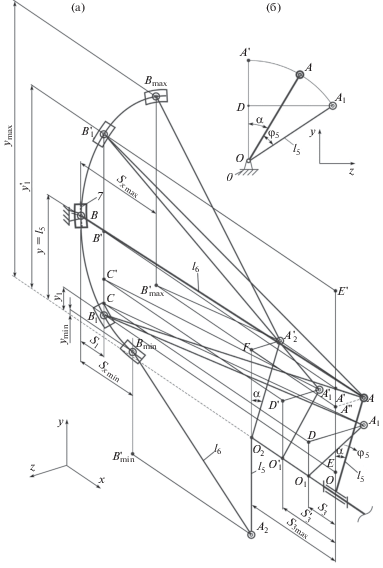
Рис. 1.
Структурная схема рычажного вариатора: 1 – кривошип; 2 – шатун; 3 – ползун; 4 – ведомый кривошип; 5, 5' – коромысло; 6, 6' – вспомогательный шатун; 7 – камень; 8 – механизм свободного хода.
Устройство и принцип работы рычажного вариатора. В рычажном вариаторе (рис. 1а) направляющая ползуна 3 пространственного механизма установлена с эксцентриситетом е, равным длине кривошипа, l1 = e.
Второй конец ползуна 3 соединен с ведомым кривошипом 4 с возможностью поступательного перемещения в осевом направлении. К кривошипно-ползунному механизму присоединен преобразующий механизм, состоящий из двух одинаковых по длине коромысел 5 и 5', вспомогательных шатунов 6 и 6', камня 7 и МСХ 8. Коромысла 5 и 5' подвижно установлены в средней части ползуна 3, а также дополнительно соединены с ползуном 3 с помощью МСХ 8. Камень 7 перемещается по направляющей стойке 0, которая выполнена в виде дуги с радиусом, равным длине вспомогательных шатунов 6 и 6', R = l6. Для избегания заклинивания звеньев коромысла 5 и 5' установлены под углом наклона α (рис. 1б). Для уменьшения неравномерности вращения ведомого вала установлены два преобразующих механизма (рис. 1в). При вращении входного звена 1 ведомое коромысло 5 получает движение посредством шатуна 2 и ползуна 3 (рис. 1). При поступательном движении ползуна 3, коромысла 5 и 5' начинают перемещаться в противоположные друг от друга стороны на одинаковые углы φ5 и $\varphi _{5}^{'}$ соответственно (рис. 1а, б). При повороте кривошипа 1 на угол (0–180)° ползун 3 и ведомый кривошип 4 движутся сонаправлено с коромыслом 5 на угол φ5. На интервале (0–180)° поворота звена 1 коромысло 5' вращается в обратную сторону, что благодаря МСХ 8 не препятствует вращению ползуна 3 и соответственно ведомого кривошипа 4. При повороте кривошипа 1 на угол (180–360)° ползун 3 и ведомый кривошип 4 поворачиваются совместно с коромыслом 5' на угол $\varphi _{5}^{'}$ по направлению вращения кривошипа 1. В этом случае коромысло 5 вращается в обратную сторону, т.к. благодаря МСХ 8 разъединяется и не препятствует вращению ползуна 3 и соответственно ведомого кривошипа 4.
При использовании двух преобразующих механизмов (рис. 1в) в схеме рычажного вариатора в процессе поворота кривошипа 1 на угол (0–180)° вращение ползуна 3 и соответственно ведомого кривошипа 4 обеспечивается одним из двух коромысел 5 или 5'1, имеющим большую угловую скорость. А при повороте кривошипа 1 на угол (180–360)° вращение ведомого кривошипа 4 реализуется коромыслом 5' или 51, в зависимости от соотношения их угловых скоростей.
Синхронное перемещение камней 7 и 71 по дугообразным направляющим позволяет изменить угол качания коромысел φ5 и $\varphi _{5}^{'}$ и соответственно скорректировать угловую скорость ведомого кривошипа ω4, т.е. изменить передаточное отношение.
Структурный анализ рычажного вариатора направлен на оценку семейства, местных подвижностей и избыточных связей [14]. Выполним замену высших кинематических пар рычажного вариатора (рис. 1) на пары пятого класса р5, чтобы получить замещающий механизм (рис. 2) эквивалентный исходному в структурном, кинематическом и силовом отношении.
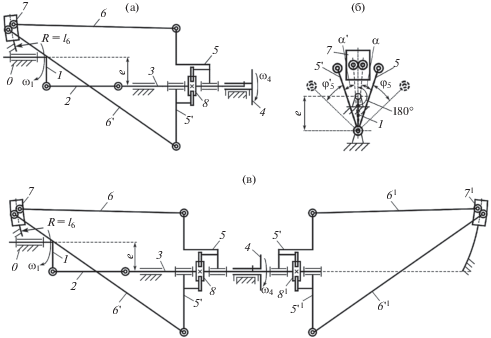
Рис. 2.
Структурная схема замещающего рычажного вариатора с кинематическими парами пятого класса: 1 – кривошип; 2 – шатун; 3 – ползун; 4 – ведомый кривошип; 5 – коромысло; 6 – вспомогательный шатун; 7 – камень; 8 – механизм свободного хода; 9, 10, 11, 12 – стержни; 13, 14 – толкатели.
Степень подвижности механизма (рис. 2) без учета ведомого кривошипа 4 равна единице, т.е. W = 6n – 5p5 = 6 × 11 – 5 × 13 = 1, иначе $W = 2$. Таким образом, исследуемый вариатор относится без учета ведомого кривошипа 4 к категории пространственных, в противном случае – к смешанной. Выходное звено может совершать движение только в одном направлении.
Структурная схема замещающего механизма рычажного вариатора (рис. 2) состоит из входного кривошипа 1, трех групп Ассура нулевого семейства $(m = 0)$ и ведомого кривошипа 4.
В каждой группе Ассура по одной кинематической паре третьего класса ${{р}_{3}}$ можно заменить на сферическую с пальцем ${{р}_{4}}$, что не повлечет изменение степени подвижности механизма, но приведет к ухудшению показателей надежности из-за возможных деформаций в процессе эксплуатации, а так же к снижению ремонтопригодности. Более целесообразно использовать в качестве ползуна 3 цилиндрическую кинематическую пару.
Кинематический расчет рычажного вариатора. Ранее кинематика четырехзвенного пространственного механизма аналогичного рассматриваемому преобразующему механизму в рычажном вариаторе (рис. 1) исследовалась в работах [15, 16]. На основе полученной зависимости, запишем перемещение ползуна 3, как функцию угла ${{\varphi }_{1}}$ вращения кривошипа 1
(1)
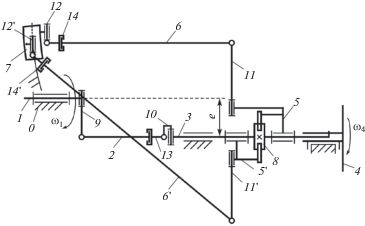
${{S}_{3}} = \sqrt {l_{2}^{2} - l_{1}^{2} - {{е}^{2}} + 2{{l}_{1}}е} - \sqrt {l_{2}^{2} - l_{1}^{2} - {{е}^{2}} + 2{{l}_{1}}е\cos {{\varphi }_{1}}} ,$На рис. 3 для нахождения зависимости ${{\varphi }_{5}}\left( {{{\varphi }_{1}}} \right)$ представлена расчетная схема кинематики рычажного вариатора при некоторых значениях: угла качения α коромысла 5, положения камня 7 и ползуна 3.
На рис. 3а изображено направление осей неподвижной декартовой системы координат XYZ, на рис. 3б – проекция коромысла ОА, качающегося относительно ползуна 3.
Вычислим расстояние ${{A}_{0}}B$, как функцию угла α поворота кривошипа 5 (рис. 3б) по известным теоремам Пифагора и косинусов
(2)
${{A}_{0}}B = \sqrt {{{{\left( {AB} \right)}}^{2}} - {{{\left( {{{A}_{0}}A} \right)}}^{2}}} = \sqrt {l_{6}^{2} - 2l_{5}^{2}\left( {1 - \cos \alpha } \right)} ,$При перемещении камня 7 по дугообразной направляющей в вертикальном направлении на расстояние у длина отрезка ${{А}_{0}}В$ уменьшится на величину ${{S}_{1}}$ (рис. 3а). Принимая отрезок $А{{В}_{1}}$ за диагональ параллелепипеда ${{В}_{1}}В_{1}^{'}A{\kern 1pt} '{\kern 1pt} А$, найдем длину отрезка ${{В}_{1}}В_{1}^{{''}}$ = ${{A}_{0}}B_{1}^{'}$
(3)
${{A}_{0}}B_{1}^{'} = \sqrt {{{{\left( {A{{B}_{1}}} \right)}}^{2}} - {{{\left( {A{\kern 1pt} '{\kern 1pt} A} \right)}}^{2}} - {{{(A{\kern 1pt} '{\kern 1pt} B_{1}^{{''}})}}^{2}}} = \sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{1}}} \right)}}^{2}}} .$Тогда отрезок ${{S}_{1}}$ определим как
(4)
${{S}_{1}} = {{A}_{0}}B - {{A}_{0}}B_{1}^{'} = \sqrt {l_{6}^{2} - 2l_{5}^{2}\left( {1 - \cos \alpha } \right)} - \sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{1}}} \right)}}^{2}}} .$Для прямоугольного треугольника $\Delta {{В}_{1}}В_{1}^{{'''}}{{А}_{1}}$ по теореме Пифагора запишем выражение для расчета ${{А}_{1}}B_{1}^{{'''}}$
(5)
${{А}_{1}}B_{1}^{{'''}} = \sqrt {{{{({{A}_{1}}{{B}_{1}})}}^{2}} - {{{({{B}_{1}}B_{1}^{{'''}})}}^{2}}} = \sqrt {l_{6}^{2} - {{{({{O}_{1}}A_{1}^{'} - {{y}_{1}})}}^{2}}} .$В прямоугольном треугольнике $\Delta B_{1}^{{'''}}A_{1}^{'}{{A}_{1}}$ по теореме Пифагора найдем длину отрезка ${{А}_{1}}B_{1}^{{'''}}$
Подставив ранее полученное выражение (3) для расчета расстояния ${{A}_{0}}B_{1}^{'}$, получим
(6)
${{А}_{1}}B_{1}^{{'''}} = \sqrt {{{{\left( {\sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{1}}} \right)}}^{2}}} - {{S}_{3}}} \right)}}^{2}} + l_{5}^{2} - {{{({{O}_{1}}A_{1}^{'})}}^{2}}} ,$Из уравнений (5) и (6) находим длину отрезка ${{O}_{1}}A_{1}^{'}$
(7)
$\begin{gathered} l_{6}^{2} - {{({{O}_{1}}A_{1}^{'} - {{y}_{1}})}^{2}} = {{\left( {\sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{1}}} \right)}}^{2}}} - {{S}_{3}}} \right)}^{2}} + l_{5}^{2} - {{({{O}_{1}}A_{1}^{'})}^{2}}, \\ {{O}_{1}}A_{1}^{'} = \frac{{{{{\left( {\sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{1}}} \right)}}^{2}}} - {{S}_{3}}} \right)}}^{2}} + l_{5}^{2} - l_{6}^{2} + y_{1}^{2}}}{{2{{y}_{1}}}}. \\ \end{gathered} $Из рис. 3б текущее значение угла поворота коромысла 5 с учетом первоначального отклонения α определим из прямоугольного треугольника $\Delta {{O}_{1}}A_{1}^{'}{{A}_{1}}$ по формуле $\cos \left( {{{\varphi }_{5}} + \alpha } \right)$ = $\frac{{{{O}_{1}}A_{1}^{'}}}{{{{O}_{1}}{{A}_{1}}}}$.
Подставив формулу (7) и используя обратную тригонометрическую функцию, оценим движение коромысла 5
(8)
${{\varphi }_{5}} = \arccos \left( {\frac{{{{{\left( {\sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{1}}} \right)}}^{2}}} - {{S}_{3}}} \right)}}^{2}} + l_{5}^{2} - l_{6}^{2} + y_{1}^{2}}}{{2{{l}_{5}}{{y}_{1}}}}} \right) - \alpha .$Определим границы диапазона регулирования положения камня 7 (рис. 3) для рассматриваемого рычажного вариатора. Минимальное вертикальное перемещение ${{y}_{{\min }}}$ звена 7 соответствует повороту кривошипа 1 на угол 180° (при этом ползун 3 перемещается на ${{S}_{{3\max }}}$), угол поворота коромысла 5 равен $\alpha + {{\varphi }_{5}}$ = 180° (рис. 3). Таким образом, составим уравнение замыкания
где ${{A}_{{2\min }}}B_{{\min }}^{'}$ = $\sqrt {{{{\left( {{{A}_{{2\min }}}{{B}_{{\min }}}} \right)}}^{2}} - {{{({{B}_{{\min }}}B_{{\min }}^{'})}}^{2}}} $ = $\sqrt {l_{6}^{2} - {{{\left( {{{l}_{5}} + {{y}_{{\min }}}} \right)}}^{2}}} $; при повороте входного кривошипа 1 на угол ${{\varphi }_{1}}$ = 180°, в соответствии с уравнением (1) и равенством ${{l}_{1}} = e$, максимальный ход ползуна составит ${{S}_{{3\max }}}$ = ${{l}_{2}}$ – $\sqrt {l_{2}^{2} - 4l_{1}^{2}} $.Подставив найденные выражения для всех составляющих в уравнение замыкания, получим
(9)
$ - \sqrt {l_{6}^{2} - {{{\left( {{{l}_{5}} + {{y}_{{\min }}}} \right)}}^{2}}} - {{l}_{2}} + \sqrt {l_{2}^{2} - 4l_{1}^{2}} + \sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{{\min }}}} \right)}}^{2}}} = 0,$Выполним алгебраические преобразования формулы (9), так чтобы записать квадратное уравнение относительно неизвестного ${{y}_{{\min }}}$
(10)
$\begin{gathered} y_{{\min }}^{2}\left( {l_{5}^{2}{{{\left( {\cos \alpha + 1} \right)}}^{2}} + {{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}}} \right) + {{y}_{{\min }}}{{l}_{5}}{{\left( {{{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} } \right)}^{2}}\left( {1 - \cos \alpha } \right) + \\ + \;{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}^{2}}\left( {l_{5}^{2} + \frac{{{{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}}}}{4} - l_{6}^{2}} \right) = 0. \\ \end{gathered} $Решив уравнение (10), сформируем условие, исключающее заклинивание звеньев при повороте коромысла 5 на угол 180°
(11)
$\begin{gathered} {{y}_{{\min }}} > \frac{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )( - {{l}_{5}}({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )\left( {1 - \cos \alpha } \right) + l{\kern 1pt} ')}}{{2(l_{5}^{2}{{{\left( {\cos \alpha + 1} \right)}}^{2}} + {{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}})}}, \\ l{\kern 1pt} ' = \sqrt {l_{5}^{2}{{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}}{{{\left( {1 - \cos \alpha } \right)}}^{2}} - 4(l_{5}^{2}{{{\left( {\cos \alpha + 1} \right)}}^{2}} + {{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}})\left( {l_{5}^{2} + \frac{{{{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}}}}{4} - l_{6}^{2}} \right)} . \\ \end{gathered} $В рычажном вариаторе максимальное перемещение камня в вертикальном направлении ${{y}_{{\max }}}$ получаем также при повороте входного кривошипа 1 на угол 180°, ползун 3 при этом находится в крайнем положении ${{S}_{{3\max }}}$. Коромысло 5 вернется в исходную позицию, т.е. ${{\varphi }_{5}} = 0$ (рис. 3). Уравнение замыкания для рассматриваемых условий запишется как ${{A}_{0}}B$ – $B_{{\max }}^{'}A_{{2\max }}^{'}$ – ${{S}_{{3\max }}}$ – ${{S}_{{x\max }}}$ = 0, где $B_{{\max }}^{'}A_{{2\max }}^{'}$ = = $\sqrt {{{{\left( {{{B}_{{\max }}}{{A}_{{2\max }}}} \right)}}^{2}} - {{{({{A}_{{2\max }}}A_{{2\max }}^{'})}}^{2}} - {{{({{B}_{{\max }}}B_{{\max }}^{'})}}^{2}}} $ или после подстановки обозначений кинематических размеров механизма $B_{{\max }}^{'}A_{{2\max }}^{'}$ = $\sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{y}_{{\max }}} - {{l}_{5}}\cos \alpha } \right)}}^{2}}} $.
Используя ранее рассчитанные выражения, уравнение замыкания для второго крайнего положения камня 7 примет вид
(12)
$\begin{gathered} - \sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{y}_{{\max }}} - {{l}_{5}}\cos \alpha } \right)}}^{2}}} - {{l}_{2}} + \sqrt {l_{2}^{2} - 4l_{1}^{2}} + \\ + \;\sqrt {l_{6}^{2} - l_{5}^{2}{{{\sin }}^{2}}\alpha - {{{\left( {{{l}_{5}}\cos \alpha - {{y}_{{\max }}}} \right)}}^{2}}} = 0. \\ \end{gathered} $Упростив уравнение (12), получим квадратное уравнение относительно неизвестного ${{y}_{{\max }}}$
(13)
$ - y_{{\max }}^{2} + 2{{l}_{5}}{{y}_{{\max }}}\cos \alpha + l_{6}^{2} - l_{5}^{2} - \frac{{{{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}}}}{4} = 0,$(14)
${{y}_{{\max }}} = {{l}_{5}}\cos \alpha \pm \sqrt {l_{5}^{2}({{{\cos }}^{2}}\alpha - 1) + l_{6}^{2} - \frac{{{{{({{l}_{2}} - \sqrt {l_{2}^{2} - 4l_{1}^{2}} )}}^{2}}}}{4}} .$Анализ результатов кинематического расчета рычажного вариатора. При проведении численного эксперимента приняты следующие значения кинематических параметров исследуемого рычажного вариатора: ${{l}_{1}} = 20$ мм; ${{l}_{2}} = 100$ мм; $e = 20$ мм; ${{l}_{5}} = 60$ мм; ${{l}_{6}} = 200$ мм; $\alpha $ = 20°.
В соответствии с уравнениями (11) и (14) рассчитаны предельные значения перемещения камня в вертикальном направлении
Для заданного положения камня $y = 13.6384$ мм по формуле (8) построен график (рис. 4) зависимости передаточного отношения (U = φ1/φ5) от угла поворота кривошипа для двух вариантов исполнения рычажного вариатора: с одним пространственным преобразующим механизмом (рис. 1а) и с двумя симметричными преобразующими механизмами (рис. 1в).
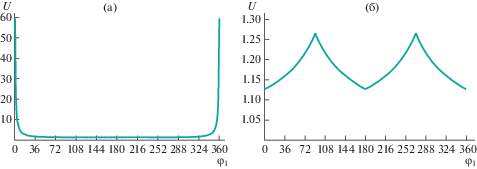
Рис. 4.
Графики изменения передаточных отношений рычажного вариатора в зависимости от угла поворота кривошипа: (а) – с одним преобразующим механизмом; (б) – с двумя преобразующими механизмами.
Коэффициент неравномерности вращения ведомого кривошипа δ определяем по формуле [17]
(15)
$\delta = \frac{{\Delta U}}{{{{U}_{{{\text{ср}}}}}}} = \frac{{2\left( {{{U}_{{\max }}} - {{U}_{{\min }}}} \right)}}{{{{U}_{{\max }}} + {{U}_{{\min }}}}},$В соответствии с формулой (15) для исследуемых рычажных вариаторов построены графики зависимости коэффициента неравномерности вращения ведомого кривошипа δ от перемещения камня по направляющей у (рис. 5).
Рис. 5.
График изменения коэффициента неравномерности вращения ведомого кривошипа рычажного вариатора δ в зависимости от перемещения камня по направляющим у: (а) – с одним преобразующим механизмом; (б) – с двумя преобразующими механизмами.
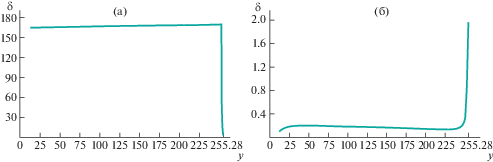
Из рис. 4, 5 следует, что при использовании в схеме рычажного вариатора одного преобразующего механизма коэффициент неравномерности вращения ведомого кривошипа δ имеет значения практически на два порядка выше, что негативно влияет на динамику устройства. Для вариатора с двумя преобразующими механизмами на рис. 6 построена диаграмма изменения среднего передаточного отношения в зависимости от перемещения камня в вертикальном направлении у.
Рис. 6.
График изменения среднего передаточного отношения рычажного вариатора с двумя преобразующими механизмами в зависимости от перемещения камня по направляющим.
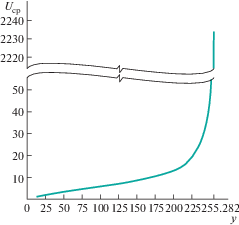
Согласно данным, представленным на рис. 6, зависимость среднего передаточного отношения Uср в рассматриваемом рычажном вариаторе от положения камня носит экспоненциальный характер. Область допустимых значений исследуемого параметра лежит в диапазоне 1.1818 ≤ ${{U}_{{{\text{ср}}}}}$ = 2233.92.
Выводы. На основе анализа конструкций современных вариаторов скоростей, показана актуальность использования рычажных схем, которые обладают повышенными показателями надежности благодаря отсутствию фрикционной передачи. Модель исследуемого плоского рычажного вариатора с пространственными преобразующими элементами более компактная, что важно при размещении в ограниченном пространстве.
Предложенная модель кинематического анализа позволила оценить предельные значения положений камня, соответствующие крайним положениям входного кривошипа и ползуна. Результаты численного эксперимента доказали, что два симметричных преобразующих механизма в схеме рычажного вариатора обеспечивают плавное регулирование передаточного отношения в широком диапазоне.
Список литературы
Сокольникова С.Р. Коробки передач современных автомобилей. Гидромеханическая и вариаторная трансмиссии // European Scientific Conference: сборник статей XVI Международной научно-практической конференции, Пенза, 07 сентября 2019 года. Пенза: “Наука и Просвещение” (ИП Гуляев Г.Ю.), 2019. С. 46.
Ганиев Р.Ф., Глазунов В.А. Актуальные проблемы машиноведения и пути их решения // Справочник. Инженерный журнал с приложением, 2015. № S11. С. 1.
Ганиев Р.Ф., Глазунов В.А. Перспективы теории машин в связи с развитием современного машиностроения // Справочник. Инженерный журнал с приложением. 2015. № 5 (218). С. 3.
Крайнев А.Ф. Словарь-справочник по механизмам. 2-е изд., М.: Машиностроение, 1987. 560 с.
Решетов Д.Н. Детали машин: учеб. для студентов машиностроительных и механических специальностей. 4-е изд. М.: Машиностроение, 1989. 496 с.
De Freitas A., Dutson B., US Patent 20140349806 2014.
William E., Fuller J., GB Patent 25440733, 2017.
Есипенко Я.И. Механические вариаторы скорости. Киев: Изд-во тех. лит., 1961. 218 с.
Мальцев В.Ф. Механические импульсные передачи. М.: Машиностроение, 1978. 367 с.
Лаврюшин Н.П., Сущев С.А., Лапин В.В., Антонов А.В., РФ Патент 2467227, 2012.
Синицын А.А., РФ Патент 2104426, 1998.
Абдираимов А.А., Кыргызская Республика Патент 1816, 2016.
Abdiraimov A. The variator with lever mechanisms // Transactions of the Canadian Society for Mechanical Engineering. 2017. V. 41 (5). P. 724.
Дворников Л.Т. Основы всеобщей (универсальной) классификации механизмов // Теория механизмов и машин. 2011. Т. 9. № 2. С. 19.
Abdiraimov A.A., Gebel E.S. Kinematical Investigation of Spatial Slider-Crank Mechanism // The 14th IFToMM World Congress, October 25–30. Taipei, Taiwan, 2015. P. 433. https://doi.org/10.6567/IFToMM.14TH.WC.OS2.041
Гебель Е.С., Абдираимов А.А., Солонин Е.В. Кинематика четырехзвенных пространственных ползунных механизмов // Омский научный вестник. 2015. № 2 (140). С. 49.
Теория механизмов и машин: учеб. для втузов / под ред. К.В. Фролова. 3-е изд., стер. М.: Высш. шк., 2001. 496 с.: ил.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин