1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 4, 2022

Проблемы машиностроения и надежности машин, 2022, № 4, стр. 46-53

Повышение износостойкости радиального подшипника скольжения смазываемого микрополярными смазочными материалами и расплавами металлического покрытия

Д. У. Хасьянова 1, *, М. А. Мукутадзе 2, **

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

* E-mail: dinara.khasyanova@mail.ru
** E-mail: murman1963@yandex.ru

Поступила в редакцию 16.03.2021
Принята к публикации 20.04.2022

Полный текст (PDF)

Аннотация

В статье на базе асимптотического и точного автомодельного решения получена расчетная модель радиального подшипника скольжения с нестандартным опорным покрытием, адаптированным к условиям трения при смазывании жидким смазочным материалом и расплавом металлического покрытия поверхности вала обладающие при ламинарном режиме течения микрополярными реологическими свойствами. Получены аналитические зависимости для радиуса расплавленной поверхности покрытия, поля скоростей, давлений при нулевом (без учета расплава покрытия) и первом (с учетом расплава покрытия) приближения, а также для несущей способности и силе трения.

Ключевые слова: радиальный подшипник, гидродинамический режим смазывания, металлическое покрытие, микрополярный жидкий смазочный материал, адаптированный профиль

В современной технике постоянно появляются и развиваются новые направления, обеспечивающие повышение эксплуатационных параметров подшипников скольжения разной конструкции. К ним относится смазывание расплавов покрытий из металлов, а также применение нестандартного адаптированного к условиям трения или упругого опорного профиля. Применение подобных подшипников требует для их проектирования специальных инженерных расчетов, для выполнения которых разрабатываются расчетные модели.

Для подшипников скольжения разных конструкций, смазываемых жидкими смазочными материалами и расплавами металлических покрытий, в гидродинамическом режиме имеется значительное число работ [1–7]. Однако в них не учитывается целый ряд особенностей подобных трибосистем. Это самоподдерживание процесса трения в гидродинамическом режиме смазывания при постоянной подаче смазочного материала.

Разработке расчетной модели радиальных подшипников скольжения с учетом нестандартного адаптированного к условиям трения опорного профиля при смазывании жидким смазочным материалом и расплавом металлического покрытия поверхности вала, обладающим при ламинарном режиме трения микрополярными реологическими свойствами, посвящено исследование в работах [8–13].

Постановка задачи. Рассматривается установившееся течение несжимаемой жидкости и расплава покрытия в рабочем зазоре, обладающее микрополярными реологическими свойствами [14–16]. Подшипник с некруговым профилем опорной поверхности неподвижен, а вал при наличии металлического покрытия на его поверхности вращается со скоростью Ω.

В полярной системе координат (рис. 1) $(r{\kern 1pt} ',\theta )$ с полюсом в центре вала уравнения контуров вала с покрытием С1, вала с расплавленной поверхностью С0, подшипниковой втулки некруговым профилем опорной поверхности С2 и подшипниковой втулки запишутся в виде

(1)
$\begin{gathered} {{C}_{1}}:r{\kern 1pt} ' = {{r}_{0}},\quad {{C}_{0}}:r{\kern 1pt} ' = {{r}_{0}} - \lambda {\kern 1pt} 'f\left( \theta \right), \\ {{С}_{2}}:r{\kern 1pt} ' = {{r}_{1}}\left( {1 + H} \right) - a{\kern 1pt} '\sin \omega \theta ,\quad {{С}_{3}}:r{\kern 1pt} ' = {{r}_{1}}\left( {1 + H} \right), \\ \end{gathered} $
где $H = \varepsilon \cos \theta - \frac{1}{2}{{\varepsilon }^{2}}{{\sin }^{2}}\theta $ + …, $\varepsilon = \frac{e}{{{{r}_{0}}}}$.

Рис. 1.

Расчетная модель.

Исходными базовыми уравнениями являются уравнение движения несжимаемой микрополярной жидкости для “тонкого слоя”, уравнение неразрывности и уравнение, описывающее радиус расплавленного контура покрытия поверхности вала с учетом скорости диссипации механической энергии

$\left( {2\mu + \kappa } \right)\left( {\frac{{{{\partial }^{2}}{{{v}}_{\theta }}}}{{\partial r{\kern 1pt} {{'}^{2}}}} + \frac{1}{{r{\kern 1pt} '}}\frac{{\partial {{{v}}_{\theta }}}}{{\partial r{\kern 1pt} '}}} \right) = \frac{1}{{r{\kern 1pt} '}}\frac{{dp{\kern 1pt} '}}{{d\theta }} - \kappa \frac{{\partial {\kern 1pt} '{\kern 1pt} {{{v}}_{r}}}}{{\partial r{\kern 1pt} '}},$
(2)
$\gamma \left( {\frac{{{{\partial }^{2}}{v}{\kern 1pt} '}}{{\partial r{\kern 1pt} '{{{\kern 1pt} }^{2}}}} + \frac{1}{{r{\kern 1pt} '}}\frac{{\partial {v}{\kern 1pt} '}}{{\partial r{\kern 1pt} '}}} \right) = \kappa {v}{\kern 1pt} '\; + \kappa \frac{{\partial {{{v}}_{0}}}}{{\partial r{\kern 1pt} '}},\quad \frac{{\partial {v}_{{r'}}^{'}}}{{\partial r{\kern 1pt} '}} + \frac{{{{{v}}_{{r'}}}}}{{r{\kern 1pt} '}} + \frac{1}{{r{\kern 1pt} '}}\frac{{\partial {{{v}}_{\theta }}}}{{\partial \theta }} = 0,$
$\frac{{d\lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right){{r}_{0}}}}{{d\theta }}\Omega L{\kern 1pt} ' = 2\mu \int\limits_{{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)}^{{{r}_{1}}\left( {1 + H} \right) - a'\sin \omega \theta } {{{{\left( {\frac{{\partial {{{v}}_{\theta }}}}{{\partial r{\kern 1pt} '}}} \right)}}^{2}}} dr{\kern 1pt} '.$

Система уравнений (2) решается при следующих граничных условиях:

(3)
$\begin{gathered} {{{v}}_{\theta }} = 0,\quad {{{v}}_{{r'}}} = 0\quad {\text{при}}\quad r{\kern 1pt} ' = {{r}_{1}}\left( {1 + H} \right) - a{\kern 1pt} '\sin \omega \theta ; \\ {{{v}}_{{r'}}} = 0,\quad {{{v}}_{\theta }} = \Omega \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right)\quad при\quad r{\kern 1pt} ' = {{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right); \\ p{\kern 1pt} '\left( 0 \right) = p{\kern 1pt} '\left( {2\pi } \right) = {{p}_{g}};\quad {{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right) = h_{0}^{*}\quad при\quad \theta = 0,\quad \theta = 2\pi . \\ \end{gathered} $

Переход к безразмерным переменным реализуется на основе формул

(4)
$\begin{gathered} r{\kern 1pt} ' = \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right) + \delta r;\quad \delta = {{r}_{1}} - \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right); \\ {{{v}}_{{r'}}} = \Omega \delta u,\quad {{{v}}_{\theta }} = \Omega {v}\left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right); \\ p{\kern 1pt} ' = p{\kern 1pt} *{\kern 1pt} p;\quad p* = \frac{{\left( {2\mu + \kappa } \right)\Omega {{{\left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right)}}^{2}}}}{{2\delta {}^{2}}}. \\ \end{gathered} $

Выполняя подстановку (4) в систему дифференциальных уравнений (2) и (3), получим

(5)
$\begin{gathered} \frac{{{{\partial }^{2}}u}}{{\partial {{r}^{2}}}} + {{N}^{2}}\frac{{\partial \upsilon }}{{\partial r}} = \frac{{dp}}{{d\theta }};\quad \frac{{{{\partial }^{2}}\upsilon }}{{\partial {{r}^{2}}}} = \frac{\upsilon }{{{{N}_{1}}}} + \frac{1}{{{{N}_{1}}}}\frac{{du}}{{dr}};\quad \frac{{\partial u}}{{\partial \theta }} + \frac{{\partial {v}}}{{\partial r}} = 0; \\ - \frac{{d\Phi \left( \theta \right)}}{{d\theta }} = K{{\int\limits_{ - \Phi \left( \theta \right)}^{1 + \eta \cos \theta - {{\eta }_{1}}\sin \omega \theta } {\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial r}}} \right)} }^{2}}dr, \\ \end{gathered} $
(6)
$\begin{gathered} u = 0,\quad {v} = 0,\quad \upsilon = 0\quad {\text{при}}\quad r = 1 + \eta \cos \theta - {{\eta }_{1}}\sin \omega \theta = h\left( \theta \right); \\ u = 1,\quad \upsilon = 0,\quad {v} = 1\quad {\text{при}}\quad r = {{r}_{0}} - \Phi \left( \theta \right);\quad p\left( 0 \right) = p\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}, \\ \end{gathered} $
где

$K = \frac{{\left( {2\mu + \kappa } \right)\Omega \left( {{{r}_{0}} - \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)} \right)}}{{L{\kern 1pt} '{\kern 1pt} \delta }};\quad \Phi \left( \theta \right) = \lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right);$
${{N}^{2}} = \frac{\kappa }{{2\mu + \kappa }};\quad {{N}_{1}} = \frac{{2\mu {{l}^{2}}}}{{{{\delta }^{2}}\kappa }};\quad {{l}^{2}} = \frac{\gamma }{{4\mu }};\quad \eta = \frac{e}{\delta };\quad {{\eta }_{1}} = \frac{{a{\kern 1pt} '}}{\delta }.$

В качестве малого параметра принимая K, обусловленного расплавом и скоростью диссипации энергии, асимптотическое решение системы дифференциальных уравнений (5) с учетом граничных условий (6) находим в виде

${v}\left( {r,\theta } \right) = {{{v}}_{0}}\left( {r,\theta } \right) + K{{{v}}_{1}}\left( {r,\theta } \right) + {{K}^{2}}{{{v}}_{2}}\left( {r,\theta } \right) + ...;$
(7)
$\begin{gathered} u\left( {r,\theta } \right) = {{u}_{0}}\left( {r,\theta } \right) + K{{u}_{1}}\left( {r,\theta } \right) + {{K}^{2}}{{u}_{2}}\left( {r,\theta } \right) + ...; \\ \Phi \left( \theta \right) = - K{{\Phi }_{1}}\left( \theta \right) - {{K}^{2}}{{\Phi }_{2}}\left( \theta \right) - {{K}^{3}}{{\Phi }_{3}}\left( \theta \right) - \ldots ; \\ \end{gathered} $
$p\left( \theta \right) = {{p}_{0}}\left( \theta \right) + K{{p}_{1}}\left( \theta \right) + {{K}^{2}}{{p}_{2}}\left( \theta \right) + {{K}^{3}}{{p}_{3}}\left( \theta \right) \ldots .$

Выполняя подстановку (7) в систему дифференциальных уравнений (5), с учетом граничных условий (6), получим уравнения

– для нулевого приближения

(8)
$\frac{{{{\partial }^{2}}{{u}_{0}}}}{{\partial {{r}^{2}}}} + \frac{{{{N}^{2}}}}{{2{{N}_{1}}h}}\left( {2r - h} \right) = \frac{{d{{p}_{0}}}}{{d\theta }},\quad \frac{{\partial {{{v}}_{0}}}}{{\partial r}} + \frac{{\partial {{u}_{0}}}}{{\partial \theta }} = 0,$
с граничными условиями

(9)
$\begin{gathered} {{{v}}_{0}} = 0,\quad {{u}_{0}} = 0,\quad {{\upsilon }_{0}} = 0\quad {\text{при}}\quad r = 1 + \eta \cos \theta - {{\eta }_{1}}\sin \omega \theta ; \\ {{{v}}_{0}} = 0,\quad {{u}_{0}} = 1,\quad {{\upsilon }_{0}} = 0\quad {\text{при}}\quad r = {{r}_{0}} - \Phi \left( \theta \right) = 0;\quad {{p}_{0}}\left( 0 \right) = {{p}_{0}}\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}; \\ \end{gathered} $

– для первого приближения:

(10)
$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{r}^{2}}}} = \frac{{d{{p}_{1}}}}{{d\theta }},\quad \frac{{\partial {{{v}}_{1}}}}{{\partial r}} + \frac{{\partial {{u}_{1}}}}{{\partial \theta }} = 0, \\ - \frac{{d{{\Phi }_{1}}\left( \theta \right)}}{{d\theta }} = K\int\limits_{\tilde {\Phi }}^{h\left( \theta \right)} {{{{\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)}}^{2}}dr} , \\ \end{gathered} $
с граничными условиями

${{{v}}_{1}} = {{\left. {\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial r}}} \right)} \right|}_{{r = 0}}} \cdot \tilde {\Phi };\quad {{u}_{1}} = {{\left. {\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)} \right|}_{{r = 0}}} \cdot \tilde {\Phi };$
(11)
${{{v}}_{1}} = 0,\quad {{u}_{1}} = 0\quad {{\upsilon }_{1}} = 0\quad {\text{при}}\quad r = h\left( \theta \right) + \tilde {\Phi };$
${{p}_{1}}\left( 0 \right) = {{p}_{1}}\left( {2\pi } \right) = 0,\quad \Phi \left( 0 \right) = \Phi \left( {2\pi } \right) = h_{0}^{*}.$

Точное автомодельное решение задачи для нулевого приближения будем искать по известному методу, в результате для поля скоростей и давлений получим

(12)
$\begin{gathered} \tilde {\psi }_{0}^{{'''}} = {{{\tilde {С}}}_{2}},\quad \tilde {u}_{0}^{{''}} = {{{\tilde {С}}}_{1}} - \frac{{{{N}^{2}}}}{{2{{N}_{1}}}}\left( {2\xi - 1} \right),\quad \tilde {u}_{0}^{'}\left( \xi \right) + \xi {\tilde {v}}_{0}^{'}\left( \xi \right) = 0; \\ \frac{{d{{p}_{0}}}}{{d\theta }} = \frac{{{{{\tilde {С}}}_{1}}}}{{{{h}^{2}}\left( \theta \right)}} + \frac{{{{{\tilde {С}}}_{2}}}}{{{{h}^{3}}\left( \theta \right)}}; \\ \end{gathered} $
и граничные условия

(13)
$\begin{gathered} \upsilon \left( 0 \right) = 0;\quad \tilde {\psi }_{0}^{'}\left( 0 \right) = 0,\quad \tilde {\psi }_{0}^{'}\left( 1 \right) = 0,\quad \tilde {u}_{0}^{'}\left( 1 \right) = 0;\quad {\tilde {v}}_{0}^{'}\left( 1 \right) = 0; \\ \upsilon \left( 1 \right) = 0;\quad {{{\tilde {u}}}_{0}}\left( 0 \right) = 1;\quad {{{{\tilde {v}}}}_{0}}\left( 0 \right) = 0;\quad \int\limits_0^1 {{{{\tilde {u}}}_{0}}\left( \xi \right)} d\xi = 0;\quad {{p}_{1}}\left( 0 \right) = {{p}_{1}}\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}. \\ \end{gathered} $

Непосредственным интегрированием получим

(14)
$\begin{gathered} \tilde {\psi }_{0}^{'}\left( \xi \right) = \frac{{{{{\tilde {С}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right),\quad {{{\tilde {u}}}_{0}} = {{{\tilde {С}}}_{1}}\frac{{{{\xi }^{2}}}}{2} - \frac{{{{N}^{2}}}}{{2{{N}_{1}}}}\left( {\frac{{{{\xi }^{3}}}}{3} - \frac{{{{\xi }^{2}}}}{2}} \right) - \left( {\frac{{{{N}^{2}}}}{{12{{N}_{1}}}} + \frac{{{{{\tilde {С}}}_{1}}}}{2} + 1} \right)\xi + 1, \\ {{{\tilde {C}}}_{1}} = 6. \\ \end{gathered} $

Из условия ${{p}_{0}}\left( 0 \right) = {{p}_{0}}\left( {2\pi } \right) = \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}$ получим выражение

(15)
${{\tilde {С}}_{2}} = - {{\tilde {С}}_{1}}\left( {1 + \frac{{{{{{\eta }}}_{1}}}}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right).$

С учетом (15) для давления получим

(16)
${{p}_{0}} = 6\left( {\eta \sin \theta + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos \omega \theta - 1} \right) - \frac{{{{\eta }_{1}}\theta }}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right) + \frac{{{{p}_{g}}}}{{p{\kern 1pt} *}}.$

Для определения ${{\Phi }_{1}}\left( \theta \right)$ с учетом уравнения (18) и $\Phi \left( 0 \right) = h_{0}^{*}$ придем к уравнению

(17)
${{\Phi }_{1}}\left( \theta \right) = \left( {\theta - \eta \sin \theta - \frac{{{{\eta }_{1}}}}{\omega }\cos \omega \theta } \right)\left( {1 - \frac{{{{N}^{4}}}}{{720N_{1}^{2}}}} \right) + h_{0}^{*}.$

Аналогично нулевому приближению для первого приближения с учетом расплава поверхности покрытия для поля скоростей и давлений получим

$\tilde {\psi }_{z}^{'}\left( \xi \right) = \frac{{{{{\tilde {\tilde {С}}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right),\quad {{\tilde {u}}_{1}}\left( \xi \right) = {{\tilde {\tilde {С}}}_{1}}\frac{{{{\xi }^{2}}}}{2} - \left( {\frac{{{{{\tilde {\tilde {С}}}}_{1}}}}{2} + M} \right)\xi + M,\quad {{\tilde {\tilde {C}}}_{1}} = 6M.$

Из условия${{p}_{1}}\left( 0 \right) = {{p}_{1}}\left( {2\pi } \right) = 0$

${{\tilde {\tilde {С}}}_{2}} = - 6M\left( {1 + \frac{{{{{{{\tilde {\eta }}}}}_{1}}}}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right)\left( {1 + \tilde {\Phi }} \right).$

С учетом (26)

(18)
${{p}_{1}} = 6M\frac{{\left( {\tilde {\eta }\sin \theta + \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos \omega \theta - 1} \right) - \frac{{{{{\tilde {\eta }}}_{1}}\theta }}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right)} \right)}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}},$
где

$\begin{gathered} M = \mathop {\sup }\limits_{\theta \in \left[ {0;2\pi } \right]} {{\left. {\left( {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right)} \right|}_{{r = 0}}} \cdot {{\Phi }_{1}}\left( \theta \right) = \\ = \mathop {\sup }\limits_{\theta \in \left[ {0;2\pi } \right]} \left| { - 1 + 4\eta \cos \theta + 2{{\eta }_{1}}\sin \omega \theta + \frac{{3{{\eta }_{1}}}}{{2\pi \omega }}\left( {\cos 2\pi \omega - 1} \right) + \frac{{{{N}^{2}}}}{{4{{N}_{1}}}}\left( {1 + \cos \theta - {{\eta }_{1}}\sin \omega \theta } \right)} \right| \cdot \tilde {\Phi }, \\ \tilde {\eta } = \frac{\eta }{{1 + \tilde {\Phi }}},\quad {{{\tilde {\eta }}}_{1}} = \frac{{{{\eta }_{1}}}}{{1 + \tilde {\Phi }}}. \\ \end{gathered} $

С учетом (8), (10), (16) и (18) для несущей способности и силы трения получим

${{R}_{x}} = p{\kern 1pt} *{\kern 1pt} {{r}_{0}}\int\limits_0^{2\pi } {\left( {{{p}_{0}}--\frac{{{{p}_{g}}}}{{p{\kern 1pt} *}} + K{{p}_{1}}} \right)\cos \theta } d\theta = 0;$
${{R}_{y}} = p{\kern 1pt} *{\kern 1pt} {{r}_{0}}\int\limits_0^{2\pi } {\left( {{{p}_{0}}--\frac{{{{p}_{g}}}}{{p{\kern 1pt} *}} + K{{p}_{1}}} \right)\sin \theta } d\theta = $
(19)
$\begin{gathered} = \frac{{\left( {2\mu + \kappa } \right)r_{0}^{3}}}{{{{\delta }^{2}}}}\left( {\eta \pi + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right) + KM\left( {\frac{{\pi \tilde {\eta } + \frac{{{{{\tilde {\eta }}}_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right)}}{{{{{\left( {1 + \tilde {\Phi }} \right)}}^{2}}}}} \right)} \right); \\ {{L}_{{тр}}} = \mu \int\limits_0^{2\pi } {\left[ {{{{\left. {\frac{{\partial {{u}_{0}}}}{{\partial r}}} \right|}}_{{r = 0}}} + K{{{\left. {\frac{{\partial {{u}_{1}}}}{{\partial r}}} \right|}}_{{r = 0}}}} \right]d\theta = } \\ \end{gathered} $
$ = \left( {2\mu + \kappa } \right)\left[ { - 2\pi + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right) + \frac{{{{N}^{2}}}}{{4{{N}_{1}}}}\left( {2\pi + \frac{{{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right)} \right) + } \right.$
$\left. {^{{^{{^{{}}}}}} + \;\tilde {\Phi }K\left( {2\pi - \frac{{2{{\eta }_{1}}}}{\omega }\left( {\cos 2\pi \omega - 1} \right)} \right)} \right].$

На основе численного анализа построены графики (рис. 2).

Рис. 2.

Влияние параметра ω, характеризующего адаптированный профиль, и теплового параметра K, характеризующего расплав, на величину: (а) – нагрузочной способности; (б) – силы трения.

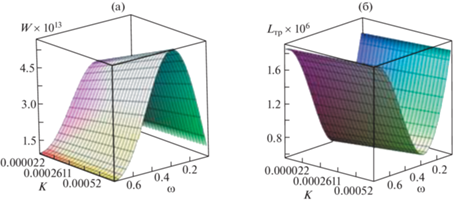
Заключительным этапом теоретических исследований является численный анализ полученных расчетных моделей. Анализ его результатов показал, что несущая способность подшипников может быть повышена в диапазоне исследований нагрузочно-скоростных режимов, на 14–16% при этом коэффициент трения снижается на 12–14%.

Экспериментальные исследования проводились с целью верификации и подтверждения эффективности полученных теоретических моделей. В первом случае исследовалось легкоплавкое металлическое покрытие; во втором – дополнительно модифицированный опорный профиль подшипниковой втулки. Исследование проводилось на модернизированной машине трения модели ИИ5018 на образцах в виде частичных вкладышей. Результаты представлены в табл. 1.

Таблица 1.

Сравнительный анализ результатов исследования легкоплавкого покрытия

№ Режимы нагружения Коэффициент трения Погрешность, %
теоретический результат экспериментальный результат
покрытие покрытие и адаптированный профиль покрытие покрытие и адаптированный профиль покрытие покрытие и адаптированный профиль
$\sigma $, МПа ${v}$, м/с
1 2 0.5 0.0032 0.0013 0.0034 0.0014 5–8 6–9
2 4 0.5 0.0033 0.0015 0.0036 0.0017
3 2 3.0 0.0035 0.0017 0.0040 0.0018
4 4 3.0 0.0038 0.0018 0.0043 0.0020

Анализ полученных результатов подтверждает эффективность теоретических расчетных моделей и доказывает преимущество исследованных подшипников скольжения, обеспечивающих повышение несущей способности и снижения коэффициента трения.

Выводы. Разработаны новые многопараметрические модели для инженерных расчетов основных рабочих характеристик (несущая способность и коэффициента трения) радиальных подшипников скольжения.

Расчетные модели учитывают применение для дополнительного смазывания расплава металлического покрытия, нестандартный адаптированный к условиям трения опорный профиль подшипниковой втулки.

Применение исследованных радиальных подшипников скольжения значительно повышает их трибохарактеристики: несущая способность увеличивается на 16%, а коэффициент трения снижается на 12%.

Условные обозначения:

${{r}_{0}}$ – радиус вала с легкоплавким покрытием;

r1 – радиус подшипниковой втулки;

е – эксцентриситет;

ε – относительный эксцентриситет;

$\lambda {\kern 1pt} '{\kern 1pt} f\left( \theta \right)$ – функция, определяющая профиль расплавленного контура покрытия вала;

$a{\kern 1pt} '$ и ω – амплитуда возмущения и параметр адаптированного профиля втулки соответственно;

${{{v}}_{{r'}}}$, ${{{v}}_{\theta }}$ – компоненты вектора скорости смазочной среды;

$p{\kern 1pt} '$ – гидродинамическое давление смазочного материала в рабочем зазоре;

$\upsilon {\kern 1pt} '$ – скорость частиц в микрополярной среде;

$L{\kern 1pt} '$ – удельная теплота плавления подшипника вала;

μ, κ, γ – параметры микрополярного смазочного материала.

Список литературы

  1. Ahamed A.R., Asokan P., Aravindan S. et al. Drilling of hybrid Al-5%SiCp-5%B4Cp metal matrix composites // Int. J. Adv. Manuf. Technol. 2010. V. 49. P. 871. https://doi.org/10.1007/s00170-009-2453-5

  2. Goto H., Omori S. Tribological characteristics of particle and chopped fiber-reinforced Al-Si alloy matrix composites // Tribol. Trans. 2000. V. 43. P. 57. https://doi.org/10.1080/10402000008982313

  3. Selvam P.T., Pugazhenthi R., Dhanasekaran C., Chandrasekaran M., Sivaganesan S. Experimental investigation on the frictional wear behaviour of TiAlN coated brake pads // Mater. Today. Proc. 2020. V. 37. P. 2419. https://doi.org/10.1016/j.matpr.2020.08.272

  4. Shapovalov V.V., Stcherbak P.N., Kornienko R.A. Forecast of frictional bonds abnormal status // Lecture Notes in Mechanical Engineering. 2019. P. 1127. https://doi.org/10.1007/978-3-319-95630-5_118

  5. Krishna U.G., Auradi V., Vasudeva B., Kori S.A. Processing and microstructural characterization of cermet-reinforced aluminium matrix composite by solidification process // Trans. Indian. Inst. Met. 2018. V. 71 (11). P. 2851. https://doi.org/10.1007/s12666-018-1432-7

  6. Кропачев Д.Ю., Гришин А.А., Масло А.Д. Способы оперативного измерения температуры расплава металлов для нужд машиностроительных предприятии // Литье и металлургия. 2012. № 3 (66). С. 126.

  7. Wang Y.C., Lin F.Y., Jian H.Z., Yuan W.M. Investigation on frictional characteristic of deep-groove ball bearings subjected to radial loads // Advances in Mechanical Engineering. 2015. V. 7 (7). P. 1. https://doi.org/10.1177/1687814015586111

  8. Tala-Ighil N., Fillon M., Maspeyrot P. Effect of textured area on the performances of a hydrodynamic journal bearing // Tribology International. 2011. V. 44 (3). P. 211. https://doi.org/10.1016/j.triboint.2010.10.003

  9. Ausas R., Ragot P., Leiva J.J.M., Bayada G., Buscaglia G.C. The impact of the cavitation model in the analysis of microtextured lubricated journal bearings // Journal of Tribology-Transactions of the Asme. 2007. V. 129 (4). P. 868. https://doi.org/10.1115/1.2768088

  10. Tala-Ighil N., Maspeyrot P., Fillon M., Bounif A. Effects of surface texture on journal-bearing characteristics under steady-state operating conditions // Proceedings of the Institution of Mechanical Engineers Part J-Journal of Engineering Tribology. 2007. V. 221 (J6). P. 623. https://doi.org/10.1243/13506501JET287

  11. Sun J., Gui C.L. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation // Tribology International. 2004. V. 37 (10). P. 841. https://doi.org/10.1016/j.triboint.2004.05.007

  12. Qiu M.F., Delic A., Raeymaekers B. The Effect of Texture Shape on the Load-Carrying Capacity of Gas-Lubricated Parallel Slider Bearings // Tribology Letters. 2012. V. 48 (3). P. 315. https://doi.org/10.1007/s11249-012-0027-4

  13. Liu H.P., Xu H., Ellison P.J., Jin Z.M. Application of Computational Fluid Dynamics and Fluid-Structure Interaction Method to the Lubrication Study of a Rotor-Bearing System // Tribology Letters. 2010. V. 38 (3). P. 325. https://doi.org/10.1007/s11249-010-9612-6

  14. Gao G.Y., Yin Z.W., Jiang D., Zhang X.L. Numerical analysis of plain journal bearing under hydrodynamic lubrication by water // Tribology International. 2014. V. 75. P. 31. https://doi.org/10.1016/j.triboint.2014.03.009

  15. Mukutadze M.A., Khasyanova D.U. Radial Friction Bearing with a Fusible Coating in the Turbulent Friction Mode // Journal of Machinery Manufacture and Reliability. 2019. № 48. P. 423.

  16. Mukutadze M.A., Khasyanova D.U. Optimization of the Supporting Surface of a Slider Bearing according to the Load-Carrying Capacity Taking into Account the Lubricant Viscosity Depending on Pressure and Temperature // Journal of Machinery Manufacture and Reliability. 2018. № 4. P. 356.

  17. Приходько В.М., Котельницкая Л.И. Математическая модель гидродинамической смазки при плавлении опорной поверхности радиального подшипника // Трение и износ. 2001. Т. 22. № 6. С. 606.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал