1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2022

Проблемы машиностроения и надежности машин, 2022, № 5, стр. 27-42

Анализ свободных колебаний скошенной ортотропной композитной панели

Н. С. Азиков 1, *, А. В. Зинин 2

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

* E-mail: nik_azikov@mail.ru

Поступила в редакцию 06.04.2022
После доработки 17.05.2022
Принята к публикации 21.06.2022

Полный текст (PDF)

Аннотация

Проведен анализ свободных колебаний и устойчивости симметричных по толщине слоистых косоугольных композитных панелей. Панель моделируется пластиной, имеющей в плане форму параллелограмма, каждый край которого может иметь независимый способ закрепления. Решение задачи поперечных колебаний и устойчивости осуществляется в перемещениях методом Ритца. Получены значения собственных частот колебаний и критических усилий сжатия скошенных слоистых композитных панелей с различными граничными условиями на контуре в зависимости от геометрии элемента, граничных условий на контуре и уровней осевой нагрузки.

Ключевые слова: композитные материалы, скошенные панели, угол скоса, свободные колебания, частота колебаний, устойчивость

Успешное применение полимерных композиционных материалов в технических системах и объектах в значительной степени определяется технологическими возможностями их производства и структурными особенностями композитов как гетерогенных материалов. В результате наиболее эффективными в этой области инженерными решениями стали тонкостенные многослойные композитные конструкции, конструктивно-технологические параметры которых в наибольшей степени соответствуют требованиям функциональности и надежности всей конструкции и наилучшим образом реализуют преимущества композитных материалов. Так, тонкостенные композитные конструкции можно выполнить в виде слоистых пластин, имеющих форму параллелограмма, стороны которого адекватны локальной системе координат конструктивного узла, в состав которого входит панель [1–5]. Тонкостенные композитные панели скошенной формы широко и эффективно применяются в качестве несущих и формообразующих элементов в конструкциях авиакосмической и автомобильной техники, в агрегатах морских судов и машиностроения, объектах строительства и гидротехнических сооружений, приборостроения и др. Скошенные панели применяются в обшивке стреловидных крыльев и хвостового оперения самолетов [6, 7] и корпусов кораблей [8], сетчатых (анизогридных) каркасов [9], элементы оболочек и лонжеронов летательных аппаратов [10], панели солнечных батарей космического аппарата [11], узлов строительных сооружений [12] и др.

Условия эксплуатации композитных элементов для указанных областей применения таковы, что композитные обшивки и панели подвергаются многократному воздействию интенсивных аэродинамических и функциональных нагрузок, которые могут приводить к динамическим эффектам, колебаниям, резонансным явлениям, и как следствие, – к разрушению. В таких условиях несущую способность элементов конструкции и прочностную надежность всего объекта во многом определяет динамическая реакция отдельных конструктивных элементов, и динамический анализ и определение частотных характеристик и форм колебаний является обязательным условием проектирования надежных и долговечных конструкций из полимерных композитов.

Обзор литературы. Свободные колебания многослойных анизотропных пластин изучали многие исследователи, которыми были предложены различные кинематические модели для прогнозирования динамического поведения композитных конструкций в зависимости от различных факторов – граничных условий, условий нагружения и геометрии конструкций. Однако методы и результаты динамического анализа композитных косоугольных пластин в современной литературе представлены ограничено. Это связано, прежде всего, со сложностью расчетных методов анализа косоугольных анизотропных объектов и определенными вычислительными трудностями из-за использования неортогональной системы координат, когда строгие формулировки при решении основных уравнений требуют дополнительных ресурсов [3, 5].

Анализ современных исследований свободных колебаний косоугольных композитных панелей показал, что классическая теория пластин Кирхгофа (CLPT) [1, 2, 13] и теория деформации сдвига Уфлянда–Миндлина (FSDT) [14–16] являются наиболее используемыми при решении динамических задач теориями пластин. Более сложные трехмерные теории, в которых каждый слой рассматривается как однородная анизотропная среда [1, 12], трудно реализуемы вычислительно при увеличении количества слоев пластины. Теория эквивалентной однослойной пластины (ESL) [2] позволяет свести трехмерную задачу теории упругости к двумерной путем принятия подходящих допущений относительно изменения смещений и напряжений по толщине пластины.

Однако ограничения теорий Кирхгофа и Уфлянда–Миндлина, не учитывающих наличие или изменение по толщине деформации поперечного сдвига, вызвали развитие уточненных методов анализа композитных пластин на основе теории сдвиговой деформации высшего порядка (HSDT) [2, 17], которая не требует поправочных коэффициентов сдвига из-за более реалистичного представления деформации поперечного сечения. Чаще всего для этого в модели вводят некоторые функции формы, в которых компоненты перемещения представлены степенным рядом по координате толщины. Поэтому в настоящее время получили распространение полиномиальная теория высшего порядка, обладающая высокой точностью [12, 18], менее трудоемкая не полиномиальная теория высшего порядка [19], теория “зигзага” Муроками [20], в которой повышенная точность результатов достигается за счет включения зигзагообразной функции для аппроксимации перемещений по толщине пластины, и другие.

Как правило, для решения задач свободных колебаний композитных пластин неортогональной формы применяют приближенные аналитические или численные методы. Известные вычислительные процедуры, такие как разложение в ряд, методы Рэлея–Ритца, расширенный метод Канторовича, безэлементный метод Галеркина, метод подвижных наименьших квадратов Ритца и др. обладают высокой точностью, но являются трудоемкими при расчетах пластин со сложной геометрией и нетрадиционными граничными условиями. В последнее время появились более производительные методы дифференциальных квадратур, методы дискретной сингулярной свертки и бессеточные методы, которые становятся все более популярными при численном решении начальных и краевых задач в инженерных приложениях. Эти методы могут дать точные решения при динамическом анализе с относительно меньшими затратами вычислительных ресурсов.

Таким образом, теория сдвиговой деформации первого порядка (FSDT) Миндлина на сегодняшний день является наиболее широко используемой теорией для динамического анализа скошенных слоистых панелей, а дифференциальный квадратурный метод (DQM), метод Рэлея–Ритца и метод конечных элементов МКЭ – наиболее часто применяемые численные методы для решения этой проблемы. Обширный обзор современных достижений в области статического и динамического анализа композитных слоистых косоугольных пластин представлен в [18]. Кратко остановимся на наиболее важных работах последних лет, не вошедших в упомянутый обзор.

Заслуживает внимания одна из немногих экспериментальных работ [21], в которой представлены экспериментальные и конечно-элементные исследования свободных колебаний изотропных и многослойных композитных скошенных пластин. Было изучено влияние угла скоса и соотношения сторон на собственные частоты косоугольных пластин. Расчетные значения собственных частот определены конечно-элементным анализом с использованием элементов CQUAD8; экспериментальные характеристики колебательного процесса получены при проведении пинг-теста модельных образцов композитных панелей. Моделирование показало, что все экспериментальные значения частот меньше полученных МКЭ, а также установлено, что расхождение расчетных и экспериментальных результатов увеличивается с увеличением угла скоса панелей.

В работе [22] представлено исследование вибрации композитных панелей численным методом – методом движущихся наименьших квадратов Ритца (MLS-Ritz), позволяющим устранить вычислительные трудности при динамическом анализе пластины с большим углом наклона из-за медленной сходимости вследствие сингулярности напряжений в тупых углах пластины.

Развитием численного анализа ортотропных пластин является метод DSC-Ritz, разработанный для анализа свободных колебаний пластин и оболочек в работе [23], который сочетает локальные базисы приближений дискретной сингулярной свертки (DSC) и метод Рэлея–Ритца с двумерными полиномиальными граничными функциями. Математической основой алгоритма DSC является теория распределений и вейвлет-анализ. Новый подход продемонстрировал точность глобальных методов для интеграции и гибкость локальных методов для работы со сложной геометрией и граничными условиями.

Влияние нерегулярности в виде круглого выреза в скошенных слоистых пластинах на их частотные характеристики исследовано в работе [24] на основе теории деформации сдвига первого порядка методом конечных элементов в среде ANSYS. Показано, что частоты собственных колебаний для первых гармоник увеличивались с увеличением угла скоса сторон пластины, количества слоев и соотношения ширины и толщины пластины. Максимальные значения частоты собственных колебаний получены для жесткого закрепления краев пластины.

М. Гюрсес (М. Gürses) [25] применил метод дискретной сингулярной свертки (DSC) для анализа свободных колебаний симметрично армированных косоугольных пластин, используя теорию сдвиговых деформаций первого порядка. В предлагаемом подходе четырехугольная неортогональная физическая область преобразуется в прямоугольную с помощью трансформации геометрических координат. Затем процедуры DSC применяются для дискретизации преобразованного набора управляющих уравнений.

Авторы статьи [26] использовали теорию деформации сдвига первого порядка в процедуре многоквадратической радиальной базисной функции (MQRBF) для предсказания поведения свободных колебаний симметрично слоистых композитных пластин средней толщины. Поперечный прогиб и два поворота слоистой пластины независимо аппроксимируются с помощью приближения базисной функции. Численные эксперименты демонстрируют возможности и эффективность использованного метода для задач на собственные значения, а также сходимость и точность вычислений.

Для построения задачи на собственные значения, связанной с собственными частотами пластины, Ю. Киани (Y. Kiani) [27] применил метод Ритца, в котором виртуальная деформация и кинетическая энергия пластины получены с использованием теории пластин сдвиговой деформации первого порядка, а функции формы представлены ортогональными полиномами, подобранными в соответствии с процессом Грама–Шмидта. Показано, что разработанный метод решения является общим и может применяться для произвольных граничных условий пластины.

А.С. Ашур (A.S. Ashour) [28] выполнил анализ свободных колебаний тонких косоугольных пластин с жестко закрепленными краями с использованием метода конечных полос переходной матрицы (метод Канторовича). Собственные частоты пластин получены итеративно, как значения, которые приводят к сингулярности матрицы перехода после наложения конкретных граничных условий на пластины. Численные результаты получены для различных значений углов скоса панели из различных композитных материалов с различной схемой укладки слоев. Сравнение с имеющимися в литературе результатами показывают точность и эффективность метода.

Р. Кумар с соавторами (R. Kumar and al.) [17] на основе теории деформации сдвига более высокого порядка (HSDT) изучали параметрический резонанс композитных скошенных пластин, подвергающихся неоднородному и линейно изменяющемуся периодическому краевому нагружению при различных граничных условиях. Функционал полной энергии, включающий дополнительную энергию изгиба из-за изменения кривизны и энергию сдвига из-за сдвиговой деформации, решается методом Рэлея–Ритца в сочетании с функциями ортонормированных полиномов граничных характеристик. Методом Болотина получены границы области параметрического резонанса с аппроксимацией более высокого порядка. Эти границы прослеживаются периодическим решением уравнений Матье–Хилла.

Дж. Н. Редди и др. изучали поведение при свободных колебаниях многослойных композитных пластин, используя теорию сдвиговой деформации второго порядка и обобщенное решение типа Лью в сочетании с концепцией пространства состояний. В работах [2] представлены точные решения типа Навье для изгиба и собственных колебаний слоистых упругих цилиндрических и сферических оболочек на основе HSDT и результаты конечно-элементного анализа свободных колебаний многослойных пластин с антисимметричным углом наклона, включая деформацию поперечного сдвига.

Б. Адхикари (B. Adhikari) [19] использовал для анализа свободных колебаний композитных панелей неполиномиальную теорию более высокого порядка, основанную на нелинейном распределении поперечных касательных напряжений по толщине пластины. Управляющие уравнения движения выводятся с помощью уравнения Лагранжа и дискретизируются с помощью процедуры конечных элементов.

Х. Тай и С.Э. Ким [29] исследовали отклики на свободные колебания многослойных композитных пластин, используя усовершенствованную теорию пластин с двумя переменными, а П. Малекзаде [30] применил теорию тонких пластин для анализа многослойных композитных косоугольных тонких пластин методом дифференциальной квадратуры, в котором геометрическая нелинейность моделируется с использованием деформации Грина в сочетании с предположениями фон Карамана.

Особо следует отметить работы [31–33], посвященные не только определению параметров собственных колебаний косоугольных композитных панелей, но и решающие задачи оптимизации структуры таких панелей для обеспечения наилучшего динамического отклика. В этих исследованиях использована современная методология вычислительного искусственного интеллекта, позволяющая решать задачи параметрической идентификации в виде поиска хорошего начального приближения с возможностью дальнейшего уточнения найденной оценки одним из численных методов.

В [31] выполнен динамический анализ и проведена оптимизация основной частоты многослойных квадратных и скошенных пластин с использованием вариационных принципов, методологии нейронной сети и генетического алгоритма. Собственные частоты композитных пластин рассчитаны методом Рэлея–Ритца для различной геометрии пластины, углов скоса и краевых условий пластины, и предложенные нейронные сети были обучены и протестированы на основе этих данных. Генетический алгоритм и предложенные нейронные сети успешно предсказали собственные частоты композитных пластин, а предсказанные частоты и оптимальные многослойные последовательности хорошо согласуются с имеющимися в литературе. Предложенный метод находит оптимальную конструкцию, максимизирующую собственную частоту композитных пластин без получения локального оптимума для всех краевых условий и параметров конструкции. Показано, что собственные частоты косоугольных пластин увеличиваются с ужесточением условий на краях пластины. Т. Фарсади (Т. Farsadi) [32] также использовал генетический алгоритм для оптимизации собственных частот и форм колебаний композитных скошенных пластин переменной жесткости. Для решения основных уравнений движения используется обобщенный дифференциально-квадратурный метод решения. Переменная жесткость достигается путем непрерывного изменения углов волокон в соответствии с двумя выбранными функциями криволинейной траектории укладки волокна в композитных слоистых материалах. Кроме того, используются предположения о линейной кинематической деформации, а теория деформации сдвига первого порядка используется для обобщения формулировки на случай пластин средней толщины, включая эффекты поперечного сдвига. Похожие задачи динамического анализа и структурной оптимизации косоугольных композитных панелей в работе [33] решены на основе оригинального комплексного подхода, сочетающего высокую точность метода конечных элементов с возможностями искусственного интеллекта в виде реализации метаэвристических (“популяционных”) алгоритмов. Конечно-элементная модель построена согласно теории сдвиговой деформации первого порядка с учетом инерционных перемещений. Оптимизационные процедуры реализованы с использованием трех мощных метаэвристических алгоритмов, инспирированные процессами реальной природы – генетического алгоритма (genetic algorithm (GA) в его классической форме, варианта оптимизации роя частиц (particle swarm optimization (PSO) и варианта поиска с кукушкой (cuckoo search (CS)). Эти алгоритмы используют принципы искусственного интеллекта и представляют новый класс стохастических поисковых методов оптимизации структуры слоистых панелей различной геометрии для максимального улучшения их динамических характеристик.

Постановка задачи. В настоящей статье проведен анализ динамического отклика скошенной композитной панели с целью оценки частотных параметров свободных колебаний конструкции в зависимости от степени скошенности панели и граничных условий на контуре, а также рассмотрены вопросы устойчивости косоугольных композитных элементов и влияния осевой сжимающей нагрузки на динамические характеристики при колебаниях.

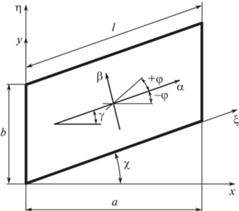
Рассмотрим многослойную углепластиковую панель (рис. 1), имеющую в плане форму параллелограмма.

Рис. 1.

Геометрические параметры косоугольной панели.

Направление армирования совпадает с осью ξ. Геометрию панели определяют следующие параметры: соотношение сторон панели ${l \mathord{\left/ {\vphantom {l b}} \right. \kern-0em} b}$ = 1, угол скоса, толщина элементарного слоя композита равна 0.15 мм; общее число слоев k = 10. Слои расположены симметрично по толщине c углами армирования $ \pm {{\varphi }_{i}}$ к продольной оси. Механические характеристики элементарного слоя углепластика со схемой армирования ${{\left[ {0^\circ {\text{/}}{\kern 1pt} \pm {\kern 1pt} 45^\circ } \right]}_{s}}$ указаны в табл. 1.

Таблица 1.

Характеристики механических свойств углепластика

Характеристика Вдоль волокон Поперек волокон
Плотность, кг/м3 1540
Модуль упругости, ГПа 110 17.5
Коэффициент Пуассона 0.260 0.041
Модуль сдвига в плоскости слоя, ГПа 7.5
Предел прочности при растяжении, МПа 1350 75
Предел прочности при сжатии, МПа 860 240
Предел прочности при сдвиге в плоскости слоя, МПа 56

Проведем исследование влияния угла скоса $\chi $ на частоту собственных колебаний и критические усилия сжатия панели в продольном направлении (рис. 1) со следующими граничными условиями (рис. 2): схема 1 – кромки слева и снизу защемлены, справа и сверху – шарнирно оперты; схема 2 – все кромки панели шарнирно оперты; схема 3 – края панели слева и снизу шарнирно оперты, справа и сверху – свободны от закрепления.

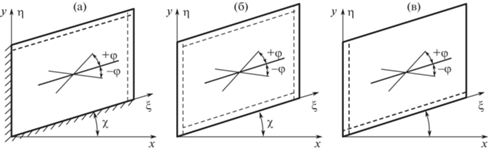
Рис. 2.

Граничные условия по контуру панели: (а) – схема 1 (З–Ш–З–Ш); (б) – схема 2 (Ш–Ш–Ш–Ш); (в) – схема 3 (Ш–С–Ш–С).

Используем полученные в [1, 3, 4] основные соотношения для косоугольных слоистых панелей, связывающие деформации и напряжения в координатах армирования $\left\{ {\alpha {\kern 1pt} \beta {\kern 1pt} z} \right\}$ элементарного слоя композитного материала, с деформациями и напряжениями в прямоугольном базисе $\left\{ {xyz} \right\}$ и деформациями и напряжениями в косоугольном базисе $\left\{ {\xi \eta z} \right\}$.

Полные деформации точек координатной поверхности в соответствующих базисах определяются следующим образом:

$\begin{gathered} {{\left\lfloor e \right\rfloor }_{{\alpha \beta }}} = {{\left\lfloor {{{e}_{\alpha }}\,{{e}_{\beta }}\,{{e}_{{\alpha \beta }}}} \right\rfloor }^{T}} = {{\left\lfloor {{{\varepsilon }_{\alpha }}\,{{\varepsilon }_{\beta }}\,{{\varepsilon }_{{\alpha \beta }}}} \right\rfloor }^{T}} + z{{\left\lfloor {{{\zeta }_{\alpha }}\,{{\zeta }_{\beta }}\,{{\zeta }_{{\alpha \beta }}}} \right\rfloor }^{T}} = \\ = \left\lfloor {{{u}_{{,\alpha }}}\,{{{v}}_{{,\beta }}}\,{{u}_{{,\beta }}} + {{{v}}_{{,\alpha }}}} \right\rfloor - z{{\left\lfloor {{{w}_{{,\alpha \alpha }}}\,{{w}_{{,\beta \beta }}}\,2{{w}_{{,\alpha \beta }}}} \right\rfloor }^{T}}, \\ \end{gathered} $
$\begin{gathered} {{\left\lfloor e \right\rfloor }_{{xy}}} = {{\left\lfloor {{{e}_{x}}\,{{e}_{y}}\,{{e}_{{xy}}}} \right\rfloor }^{T}} = {{\left\lfloor {{{\varepsilon }_{x}}\,{{\varepsilon }_{y}}\,{{\varepsilon }_{{xy}}}} \right\rfloor }^{T}} + z{{\left\lfloor {{{\zeta }_{x}}\,{{\zeta }_{y}}\,{{\zeta }_{{xy}}}} \right\rfloor }^{T}} = \\ = \left\lfloor {{{u}_{{,x}}}\,{{{v}}_{{,y}}}\,{{u}_{{,y}}} + {{{v}}_{{,x}}}} \right\rfloor - z{{\left\lfloor {{{w}_{{,xx}}}\,{{w}_{{,yy}}}2\,{{w}_{{,xy}}}} \right\rfloor }^{T}}, \\ \end{gathered} $
$\begin{gathered} {{\left\lfloor e \right\rfloor }_{{\xi \eta }}} = {{\left\lfloor {{{e}_{\xi }}\,{{e}_{\eta }}\,{{e}_{{\xi \eta }}}} \right\rfloor }^{T}} = {{\left\lfloor {{{\varepsilon }_{\xi }}\,{{\varepsilon }_{\eta }}\,{{\varepsilon }_{{\xi \eta }}}} \right\rfloor }^{T}} + z{{\left\lfloor {{{\zeta }_{\xi }}\,{{\zeta }_{\eta }}\,{{\zeta }_{{\xi \eta }}}} \right\rfloor }^{T}} = \\ = \left\lfloor {{{u}_{{,\xi }}}\,{{{v}}_{{,\eta }}}\,{{u}_{{,\eta }}} + {{{v}}_{{,\xi }}}} \right\rfloor - z{{\left\lfloor {{{w}_{{,\xi \xi }}}\,{{w}_{{,\eta \eta }}}\,2\,{{w}_{{,\xi \eta }}}} \right\rfloor }^{T}}. \\ \end{gathered} $

Деформации, определенные в различных базисах, связаны между собой соотношениями

${{\left\lfloor e \right\rfloor }_{{\alpha \beta }}} = \left[ {R_{{\alpha \beta }}^{\varepsilon }} \right]{{\left\lfloor e \right\rfloor }_{{xy}}} = \left[ {R_{{\alpha \beta }}^{\varepsilon }} \right]\left[ {R_{\varepsilon }^{{\xi \eta }}} \right]{{\left\lfloor e \right\rfloor }_{{\xi \eta }}},$
$\left[ {R_{{\alpha \beta }}^{\varepsilon }} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\cos }}^{2}}\left( {\gamma \pm \varphi } \right)}&{{{{\sin }}^{2}}\left( {\gamma \pm \varphi } \right)}&{0.5\sin 2\left( {\gamma \pm \varphi } \right)} \\ {{{{\sin }}^{2}}\left( {\gamma \pm \varphi } \right)}&{{{{\cos }}^{2}}\left( {\gamma \pm \varphi } \right)}&{ - 0.5\sin 2\left( {\gamma \pm \varphi } \right)} \\ { - \sin 2\left( {\gamma \pm \varphi } \right)}&{\sin 2\left( {\gamma \pm \varphi } \right)}&{\cos 2\left( {\gamma \pm \varphi } \right)} \end{array}} \right],$
$\left[ {R_{\varepsilon }^{{\xi \eta }}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\sec }}^{2}}\chi }&{{{{\operatorname{tg} }}^{2}}\chi }&{ - \operatorname{tg} \chi \sec \chi } \\ 0&1&0 \\ 0&{ - 2\operatorname{tg} \chi }&{\sec \chi } \end{array}} \right].$

Напряжения, возникающие в слоях композитной панели, представим в виде

${{\left\lfloor \sigma \right\rfloor }_{{\alpha \beta }}} = {{\left\lfloor {{{\sigma }_{\alpha }}\,{{\sigma }_{\beta }}\,{{\tau }_{{\alpha \beta }}}} \right\rfloor }^{T}},\quad {{\left\lfloor \sigma \right\rfloor }_{{xy}}} = {{\left\lfloor {{{\sigma }_{x}}\,{{\sigma }_{y}}\,{{\tau }_{{xy}}}} \right\rfloor }^{T}},\quad {{\left\lfloor \sigma \right\rfloor }_{{\xi \eta }}} = {{\left\lfloor {{{\sigma }_{\xi }}\,{{\sigma }_{\eta }}\,{{\tau }_{{\xi \eta }}}} \right\rfloor }^{T}},$
${{\left\lfloor \sigma \right\rfloor }_{{\alpha \beta }}} = \left[ {R_{{\alpha \beta }}^{\sigma }} \right]{{\left\lfloor \sigma \right\rfloor }_{{xy}}} = \left[ {R_{{\alpha \beta }}^{\sigma }} \right]\left[ {R_{\sigma }^{{\xi \eta }}} \right]{{\left\lfloor \sigma \right\rfloor }_{{\xi \eta }}},$
$\left[ {R_{{\alpha \beta }}^{\sigma }} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\cos }}^{2}}\left( {\gamma \pm \varphi } \right)}&{{{{\sin }}^{2}}\left( {\gamma \pm \varphi } \right)}&{\sin 2\left( {\gamma \pm \varphi } \right)} \\ {{{{\sin }}^{2}}\left( {\gamma \pm \varphi } \right)}&{{{{\cos }}^{2}}\left( {\gamma \pm \varphi } \right)}&{ - \sin 2\left( {\gamma \pm \varphi } \right)} \\ { - 0.5\sin 2\left( {\gamma \pm \varphi } \right)}&{0.5\sin 2\left( {\gamma \pm \varphi } \right)}&{\cos 2\left( {\gamma \pm \varphi } \right)} \end{array}} \right],$
$\left[ {R_{\sigma }^{{\xi \eta }}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \chi }&0&0 \\ {\sin \chi \operatorname{tg} \chi }&{\sec \chi }&{2\operatorname{tg} \chi } \\ {\sin \chi }&0&1 \end{array}} \right].$

Физические соотношения между напряжениями и деформациями получим с помощью матриц обобщенных жесткостей

${{\left\lfloor \sigma \right\rfloor }_{{\alpha \beta }}} = \left[ {{{A}^{{\alpha \beta }}}} \right]{{\left\lfloor e \right\rfloor }_{{\alpha \beta }}},\quad {{\left\lfloor \sigma \right\rfloor }_{{xy}}} = \left[ {{{A}^{{xy}}}} \right]{{\left\lfloor e \right\rfloor }_{{xy}}},\quad {{\left\lfloor \sigma \right\rfloor }_{{\xi \eta }}} = \left[ {{{A}^{{\xi \eta }}}} \right]{{\left\lfloor e \right\rfloor }_{{\xi \eta }}},{\kern 1pt} $
${{\left\lfloor \sigma \right\rfloor }_{{\alpha \beta }}} = \left[ {{{A}^{{\alpha \beta }}}} \right]{{\left\lfloor e \right\rfloor }_{{\alpha \beta }}} = \left[ {R_{{\alpha \beta }}^{\sigma }} \right]\left[ {{{A}^{{xy}}}} \right]{{\left\lfloor e \right\rfloor }_{{xy}}} = \left[ {R_{{\alpha \beta }}^{\sigma }} \right]\left[ {R_{\sigma }^{{\xi \eta }}} \right]\left[ {{{A}^{{\xi \eta }}}} \right]{{\left\lfloor e \right\rfloor }_{{\xi \eta }}}.$

Элементы обобщенных матриц в свою очередь связаны между собой следующими зависимостями:

$\left[ {{{A}^{{\alpha \beta }}}} \right] = {{\left[ {R_{{\alpha \beta }}^{\sigma }} \right]}^{{ - 1}}}\left[ {{{E}_{{\alpha \beta }}}} \right]\left[ {R_{{\alpha \beta }}^{\varepsilon }} \right],\quad \left[ {{{A}^{{\xi \eta }}}} \right] = \left[ {R_{\sigma }^{{\xi \eta }}} \right]\left[ {{{A}^{{xy}}}} \right],$
где $\left[ {{{E}_{{{{\alpha \beta }}}}}} \right]$, $\left[ {{{A}^{{xy}}}} \right]$ – квадратные матрицы приведенных модулей упругости, модуля сдвига и коэффициентов Пуассона

$\left[ {{{E}_{{\alpha \beta }}}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\overline E }}_{\alpha }}}&{{{\mu }_{{\alpha \beta }}}{{{\overline E }}_{\alpha }}}&0 \\ {{{\mu }_{{\beta \alpha }}}{{{\overline E }}_{\beta }}}&{{{{\overline E }}_{\beta }}}&0 \\ 0&0&{{{G}_{{\alpha \beta }}}} \end{array}} \right],\quad \left[ {{{A}^{{xy}}}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\overline E }}_{x}}}&{{{\mu }_{{xy}}}{{{\overline E }}_{y}}}&0 \\ {{{\mu }_{{yx}}}{{{\overline E }}_{x}}}&{{{{\overline E }}_{y}}}&0 \\ 0&0&{{{G}_{{xy}}}} \end{array}} \right],$
${{\bar {E}}_{\alpha }} = {{{{E}_{\alpha }}} \mathord{\left/ {\vphantom {{{{E}_{\alpha }}} {\left( {1 - {{\mu }_{{\alpha \beta }}}{{\mu }_{{\beta \alpha }}}} \right)}}} \right. \kern-0em} {\left( {1 - {{\mu }_{{\alpha \beta }}}{{\mu }_{{\beta \alpha }}}} \right)}},\quad {{\bar {E}}_{x}} = {{{{E}_{x}}} \mathord{\left/ {\vphantom {{{{E}_{x}}} {\left( {1 - {{\mu }_{{xy}}}{{\mu }_{{yx}}}} \right)}}} \right. \kern-0em} {\left( {1 - {{\mu }_{{xy}}}{{\mu }_{{yx}}}} \right)}}.$

Элементы матрицы вычисляются с учетом схемы армирования композитного пакета [2]

$A_{{11}}^{{\alpha \beta }} = {{\bar {E}}_{\alpha }}{{\cos }^{4}}\left( {\gamma \pm \varphi } \right) + {{\bar {E}}_{\beta }}{{\sin }^{4}}\left( {\gamma \pm \varphi } \right) + 2{{E}_{{\alpha \beta }}}{{\sin }^{2}}\left( {\gamma \pm \varphi } \right){{\cos }^{2}}\left( {\gamma \pm \varphi } \right),$
$A_{{12}}^{{\alpha \beta }} = A_{{21}}^{{\alpha \beta }} = {{\bar {E}}_{\alpha }}{{\mu }_{{\alpha \beta }}} + \left( {{{{\bar {E}}}_{\alpha }} + {{{\bar {E}}}_{\beta }} - 2{{E}_{{\alpha \beta }}}} \right){{\sin }^{2}}\left( {\gamma \pm \varphi } \right){{\cos }^{2}}\left( {\gamma \pm \varphi } \right),$
$A_{{13}}^{{\alpha \beta }} = A_{{31}}^{{\alpha \beta }} = $
$ = \sin \left( {\gamma \pm \varphi } \right)\cos \left( {\gamma \pm \varphi } \right)\left[ {{{{\bar {E}}}_{\alpha }}{{{\cos }}^{2}}\left( {\gamma \pm \varphi } \right) - {{{\bar {E}}}_{\beta }}{{{\sin }}^{2}}\left( {\gamma \pm \varphi } \right)} \right.\left. { - {{E}_{{\alpha \beta }}}\cos 2\left( {\gamma \pm \varphi } \right)} \right];$
$A_{{22}}^{{\alpha \beta }} = {{\bar {E}}_{\alpha }}{{\sin }^{4}}\left( {\gamma \pm \varphi } \right) + {{\bar {E}}_{\beta }}{{\cos }^{4}}\left( {\gamma \pm \varphi } \right) + 2{{E}_{{\alpha \beta }}}{{\sin }^{2}}\left( {\gamma \pm \varphi } \right){{\cos }^{2}}\left( {\gamma \pm \varphi } \right),$
$A_{{23}}^{{\alpha \beta }} = A_{{32}}^{{\alpha \beta }} = $
$ = \sin \left( {\gamma \pm \varphi } \right)\cos \left( {\gamma \pm \varphi } \right)\left[ {{{{\bar {E}}}_{\alpha }}{{{\sin }}^{2}}\left( {\gamma \pm \varphi } \right) - {{{\bar {E}}}_{\beta }}{{{\cos }}^{2}}\left( {\gamma \pm \varphi } \right)} \right.\left. { + {{E}_{{\alpha \beta }}}\cos 2\left( {\gamma \pm \varphi } \right)} \right],$
$A_{{33}}^{{\alpha \beta }} = \left( {{{{\bar {E}}}_{\alpha }} + {{{\bar {E}}}_{\beta }} - 2{{{\bar {E}}}_{\alpha }}{{\mu }_{{\alpha \beta }}}} \right){{\sin }^{2}}\left( {\gamma \pm \varphi } \right){{\cos }^{2}}\left( {\gamma \pm \varphi } \right) + {{G}_{{\alpha \beta }}}{{\cos }^{2}}2\left( {\gamma \pm \varphi } \right);$
${{E}_{{\alpha \beta }}} = {{\bar {E}}_{\alpha }}{{\mu }_{{\alpha \beta }}} + 2{{G}_{{\alpha \beta }}}.$

Динамический анализ косоугольной композитной панели. Уравнение колебаний панели в общем случае анизотропии свойств материала слоев имеет вид

(1)
$\begin{gathered} D_{{11}}^{{\xi \eta }}\frac{{{{\partial }^{4}}w}}{{\partial {{\xi }^{4}}}} + 4D_{{13}}^{{\xi \eta }}\frac{{{{\partial }^{4}}w}}{{\partial {{\xi }^{3}}\partial \eta }} + 2\left( {D_{{12}}^{{\xi \eta }} + D_{{33}}^{{\xi \eta }}} \right)\frac{{{{\partial }^{4}}w}}{{\partial {{\xi }^{2}}\partial {{\eta }^{2}}}} + 4D_{{23}}^{{\xi \eta }}\frac{{{{\partial }^{4}}w}}{{\partial \xi \partial {{\eta }^{3}}}} + \\ + \;D_{{22}}^{{\xi \eta }}\frac{{{{\partial }^{4}}w}}{{\partial {{\eta }^{4}}}} + {{N}_{\xi }}\frac{{{{\partial }^{2}}w}}{{\partial {{\xi }^{2}}}} + \rho h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = 0. \\ \end{gathered} $

Здесь ${{\left[ D \right]}^{{\xi \eta }}}$ – матрица изгибных жесткостей

${{\left[ D \right]}^{{\xi \eta }}} = \left[ {\begin{array}{*{20}{c}} {D_{{11}}^{{\xi \eta }}}&{D_{{12}}^{{\xi \eta }}}&{D_{{13}}^{{\xi \eta }}} \\ {D_{{21}}^{{\xi \eta }}}&{D_{{22}}^{{\xi \eta }}}&{D_{{23}}^{{\xi \eta }}} \\ {D_{{31}}^{{\xi \eta }}}&{D_{{32}}^{{\xi \eta }}}&{D_{{33}}^{{\xi \eta }}} \end{array}} \right] = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {\left[ {{{A}_{{\xi \eta }}}} \right]} zdz,$
где w, h – прогиб и толщина панели; $\rho $ – удельный вес композитного материала; ${{N}_{\xi }}$ – усилие, возникающее в панели в продольном направлении.

Полагая закон движения точек панели в виде гармонической функции $w = W\cos \omega t$, где $\omega $ – частота колебаний панели, запишем уравнение колебаний (1) в виде

$\begin{gathered} D_{{11}}^{{\xi \eta }}{{W}_{{,\xi \xi \xi \xi }}} + 4D_{{13}}^{{\xi \eta }}{{W}_{{,\xi \xi \xi \eta }}} + 2\left( {D_{{12}}^{{\xi \eta }} + D_{{33}}^{{\xi \eta }}} \right){{W}_{{,\xi \xi \eta \eta }}} + 4D_{{23}}^{{\xi \eta }}{{W}_{{,\xi \eta \eta \eta }}} + \\ + \;D_{{22}}^{{\xi \eta }}{{W}_{{,\eta \eta \eta \eta }}} + {{N}_{\xi }}{{W}_{{,\xi \xi }}} - \rho {{\omega }^{2}}h{{W}_{{,tt}}} = 0. \\ \end{gathered} $

Решение задачи поперечных колебаний скошенной панели найдем методом Релея–Ритца, для чего функцию перемещений представим в виде двойного ряда

(2)
$W = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{{A}_{{mn}}}{{{\bar {w}}}_{{1m}}}\left( \xi \right)} {{{\bar {w}}}_{{2n}}}\left( \eta \right)} ,$
где ${{A}_{{mn}}}$ – амплитуда прогиба для чисел полуволн m, n; ${{\bar {w}}_{{1m}}}$, ${{\bar {w}}_{{2n}}}$ – собственные формы, определяемые граничными условиями задачи.

Используем для представления собственных форм ${{\bar {w}}_{{1m}}}$, ${{\bar {w}}_{{2n}}}$ функции Крылова [3] в виде

(3)
$\begin{gathered} S\left( {{{\lambda }_{p}}r} \right) = \frac{1}{2}\left( {\operatorname{ch} {{\lambda }_{p}}r + \cos {{\lambda }_{p}}r} \right),\quad T\left( {{{\lambda }_{p}}r} \right) = \frac{1}{2}\left( {\operatorname{sh} {{\lambda }_{p}}r + \sin {{\lambda }_{p}}r} \right), \\ U\left( {{{\lambda }_{p}}r} \right) = \frac{1}{2}\left( {\operatorname{ch} {{\lambda }_{p}}r - \cos {{\lambda }_{p}}r} \right),\quad V\left( {{{\lambda }_{p}}r} \right) = \frac{1}{2}\left( {\operatorname{sh} {{\lambda }_{p}}r - \sin {{\lambda }_{p}}r} \right). \\ \end{gathered} $

Свойства функций Крылова позволяют успешно описывать динамические эффекты в граничных областях пластины, где наблюдается краевой эффект в виде резкого изменения перемещений и усилий. Для рассматриваемых в задаче граничных условий (рис. 2) собственные формы будут иметь вид

${\text{Схема}}\;{\text{1:}}\;\;{{\bar {w}}_{{{\text{кр}}}}}(r) = \sin ({{\lambda }_{p}}r),\quad {{\lambda }_{p}} = \frac{{\pi p}}{R};$
${\text{Схема 2:}}\;\;{{\bar {w}}_{{{\text{кр}}}}}(r) = U({{\lambda }_{p}}r) - \frac{{S({{\lambda }_{p}}R) \cdot V({{\lambda }_{p}}r)}}{{T({{\lambda }_{p}}R)}},\quad {{\lambda }_{p}} = \frac{{\pi (4p + 1)}}{{4R}};$
${\text{Схема 3:}}\;\;{{\bar {w}}_{{{\text{кр}}}}}(r) = T({{\lambda }_{p}}r) - \frac{{U({{\lambda }_{p}}R) \cdot V({{\lambda }_{p}}r)}}{{S({{\lambda }_{p}}R)}},\quad {{\lambda }_{p}} = \frac{{\pi (4p - 3)}}{{4R}},$
где $k = 1,2$; $r = \xi ,\eta $; $R = l,b$; $p = \left\{ {m,n} \right\}$ = 1, 2, 3….

Следует отметить, что вследствие неортогональности производных функций Крылова необходимо решать общую задачу на собственные значения. Для этого запишем интегральную форму функционала полной энергии деформирования панели в виде

(4)
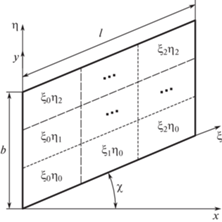
$\begin{gathered} {\text{Э}} = \frac{1}{2}\int\limits_0^l {\int\limits_0^b {\left\{ {D_{{11}}^{{\xi \eta }}{{W}_{{,\xi \xi \xi \xi }}} + 4D_{{13}}^{{\xi \eta }}{{W}_{{,\xi \xi \xi \eta }}} + 2\left( {D_{{12}}^{{\xi \eta }} + D_{{33}}^{{\xi \eta }}} \right){{W}_{{,\xi \xi \eta \eta }}} + 4D_{{23}}^{{\xi \eta }}{{W}_{{,\xi \eta \eta \eta }}} + } \right.} } \\ \left. { + \;D_{{22}}^{{\xi \eta }}{{W}_{{,\eta \eta \eta \eta }}} + {{N}_{\xi }}{{W}_{{,\xi \xi }}} - \rho {{\omega }^{2}}hW} \right\}d\xi d\eta , \\ \end{gathered} $
и подставим в нее функцию перемещения в виде ряда (2).

Для вычисления интеграла (4) воспользуемся алгоритмом Симпсона [4, 5], согласно которому область интегрирования разбивается на $t$ частей с помощью сетки координатных линий, параллельных осям $\xi $ и $\eta $ (рис. 3). Разбивая рассматриваемую область интегрирования (поверхность пластины) на 30 частей с размерностью каждой 3 × 3, получим кубатурную формулу Симпсона для вычисления интеграла полной энергии (4)

$\begin{gathered} \int\limits_0^l {\int\limits_0^b {f(\xi ,\eta )d\xi d\eta = \sum\limits_t {\sum\limits_t {\frac{{rq}}{9}} } \left\{ {f({{\xi }_{0}},{{\eta }_{0}}) + f({{\xi }_{2}},{{\eta }_{0}}) + f({{\xi }_{0}},{{\eta }_{2}}) + f({{\xi }_{2}},{{\eta }_{2}})} \right.} } + \\ \left. {\; + 4\left[ {f({{\xi }_{1}},{{\eta }_{0}}) + f({{\xi }_{0}},{{\eta }_{1}}) + f({{\xi }_{2}},{{\eta }_{1}}) + f({{\xi }_{1}},{{\eta }_{2}})} \right] + 16f({{\xi }_{1}},{{\eta }_{1}})} \right\}. \\ \end{gathered} $
Здесь $r = {b \mathord{\left/ {\vphantom {b t}} \right. \kern-0em} t}$, $q = {l \mathord{\left/ {\vphantom {l t}} \right. \kern-0em} t}$.

Рис. 3.

Представление области интегрирования панели.

Выполнив минимизацию полученного после интегрирования выражения для полной энергии по параметрам ${{A}_{{mn}}}$, получим однородную систему линейных алгебраических уравнений относительно неизвестных амплитуд ${{A}_{{mn}}}$

(5)
$\left( {\left[ \Omega \right] - {{N}_{\xi }}\left[ {{{\Upsilon }_{\xi }}} \right] - \frac{1}{4}\rho {{\omega }^{2}}hlb\left[ {\rm E} \right]} \right)\left\lfloor A \right\rfloor = 0.$

Здесь $\left[ \Omega \right] = \int_0^l {\int_0^b {{{{\left\lfloor {{{W}_{{,\xi \xi }}}\;{{W}_{{,\eta \eta }}}\;2{{W}_{{,\xi \eta }}}} \right\rfloor }}^{T}}{{{\left[ D \right]}}^{{\xi \eta }}}\left\lfloor {{{W}_{{,\xi \xi }}}\;{{W}_{{,\eta \eta }}}\;2{{W}_{{,\xi \eta }}}} \right\rfloor d\xi d\eta } } $; $\left[ {{{\Upsilon }_{\xi }}} \right]$ = $\int_0^l {\int_0^b {{{{\left( {{{W}_{{,\xi }}}} \right)}}^{2}}d\xi d\eta } } $ – квадратные матрицы коэффициентов; $\left[ {\rm E} \right]$ – единичная матрица.

Условие существования нетривиального решения однородной системы уравнений (5) в виде

(6)
$\det \left( {\left[ \Omega \right] - {{N}_{\xi }}\left[ {{{\Upsilon }_{\xi }}} \right] - \frac{1}{4}\rho {{\omega }^{2}}hlb\left[ {\rm E} \right]} \right) = 0,$
преобразуем к безразмерному виду, введя векторы безразмерных частот $\left\lfloor {{{\varsigma }^{2}}} \right\rfloor $ и $[\Omega *]$: $\left\lfloor {{{\varsigma }^{2}}} \right\rfloor $ = ${{\omega }^{2}}\frac{{\rho h{{l}^{2}}{{b}^{2}}}}{{{{\pi }^{4}}\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} }}$; $[\Omega *]$ = $\frac{{{{\pi }^{4}}}}{{{{l}^{2}}{{b}^{2}}}}\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} \left[ \Omega \right]$.

Затем из условия отсутствия сжимающих усилий в панели находим частотные параметры колебательного процесса ${{\varsigma }^{2}}$ и $\omega {\kern 1pt} *$

$\det \left( {[\Omega *] - \left\lfloor {{{\varsigma }^{2}}} \right\rfloor \left[ {\rm E} \right]} \right) = 0.$

Результаты вычисления частот свободных колебаний панелей с различными граничными условиями в зависимости от угла скоса χ представлены на рис. 4.

Рис. 4.

Изменение частотных характеристик углепластиковых панелей в зависимости от угла скоса для различных схем закрепления краев; (а) – собственная частота $\omega $; (б) – безразмерный параметр ${{\varsigma }^{2}}$; 1 – схема 1; 2 – схема 2; 3 – схема 3.

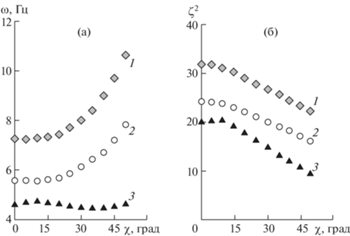
Динамический анализ косоугольных углепластиковых панелей показывает, что небольшие отступления от прямоугольной формы ($\chi $ < 25–30°) не сказываются на частотных параметрах тонкостенных композитных элементов. Для схемы закрепления с двумя свободными кромками пластины (рис. 2, схема № 3) частота собственных колебаний остается практически неизменной и для больших углов скоса $\chi $ = 50–60°. Тенденция увеличения значений собственной частоты при больших углах скоса ($\chi $ > 30°) прогнозируется расчетом для схем закрепления без свободных краев (рис. 2, схемы № 1 и 2), что обусловлено, вероятно, повышенной жесткостью всей механической системы при фиксации всего периметра пластины. Для пластин, скошенных до угла 50° и закрепленных по схемам 1 и 2, частота собственных колебаний возрастает на 40–50% по сравнению с панелями прямоугольной формы.

Учет осевой нагрузки. Проведем анализ влияния угла скоса на устойчивость и динамическое поведение панели, определив критическое значение усилия $T_{\xi }^{*}$ при осевом сжатии. Выражая критическую нагрузку через коэффициент устойчивости при продольном сжатии $k_{\xi }^{*}$ ($k_{\xi }^{*}$ = $\min \left( {\left\lfloor {{{k}_{\xi }}} \right\rfloor } \right)$) в форме

$T_{\xi }^{*} = \frac{{{{\pi }^{2}}}}{{{{b}^{2}}}}\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} k_{\xi }^{*},$
получим однородную систему уравнений (5) для продольного изгиба в виде

(7)
$\left( {[\Omega *] - {{k}_{\xi }}\left[ E \right]} \right)\left\lfloor A \right\rfloor = 0.$

В случае шарнирного опирания кромок панели (рис. 2, схема 2) элементы матрицы [Ω*] можно определить аналитически

$[\Omega *] = \left\{ \begin{gathered} {{n}^{2}}\sqrt {\frac{{D_{{11}}^{{\xi \eta }}}}{{D_{{22}}^{{\xi \eta }}}}} \frac{{\lambda _{m}^{2}}}{{\lambda _{n}^{2}}} + 2\frac{{D_{{12}}^{{\xi \eta }} + 2D_{{33}}^{{\xi \eta }}}}{{\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} }} + \sqrt {\frac{{D_{{22}}^{{\xi \eta }}}}{{D_{{11}}^{{\xi \eta }}}}} \frac{{\lambda _{n}^{2}}}{{\lambda _{m}^{2}}}, \hfill \\ - \frac{{64}}{{{{\pi }^{2}}}}\frac{{{{\lambda }_{n}}}}{{{{\lambda }_{m}}}}\frac{{ij}}{{\left( {{{m}^{2}} - {{i}^{2}}} \right)\left( {{{n}^{2}} - {{j}^{2}}} \right)}}\left[ {{{{\left( {m\frac{b}{l}} \right)}}^{2}}\frac{{D_{{13}}^{{\xi \eta }}}}{{\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} }} + {{n}^{2}}\frac{{D_{{23}}^{{\xi \eta }}}}{{\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} }}} \right]. \hfill \\ \end{gathered} \right.$

Здесь первая строка определяет соотношения для диагональных элементов матрицы, вторая – для внедиагональных элементов при $\left( {m \pm i} \right) = 1,3,5 \ldots $; $\left( {n \pm j} \right)$ = 1, 3, 5….

В остальных случаях закрепления панели матрица [Ω*] является несимметричной, поэтому для определения коэффициентов ${{\left\lfloor k \right\rfloor }_{\xi }}$ использовался двойной QR-алгоритм Френсиса [34]. Данный алгоритм заключается в построении последовательности матриц, которые при выполнении некоторых условий сходятся к верхней треугольной матрице с собственными значениями на главной диагонали. Первоначально исходная матрица приводится к верхней почти треугольной матрице Гессенберга с помощью преобразований подобия, после чего матрица Гессенберга трансформируется в верхнюю треугольную матрицу, для которой может быть определено минимальное действительное собственное значение. Методики приведения исходной несимметричной матрицы к верхней почти треугольной и поиск собственных значений верхней почти треугольной матрицы реализованы в прикладных программных комплексах [35].

Вектор коэффициентов устойчивости определим из условия равенства нулю детерминанта однородной системы уравнений (7).

Результаты вычисления коэффициентов устойчивости $k_{\xi }^{*}$ и критических усилий сжатия $T_{\xi }^{*}$ в зависимости от углов скоса приведены в табл. 2. Из расчетов следует, что абсолютные значения параметров устойчивости панелей $k_{\xi }^{*}$ и $T_{\xi }^{*}$ зависят от условий закрепления конструкции.

Таблица 2.

Расчетные значения параметров устойчивости панелей в зависимости от угла скоса $\chi $

Угол скоса $\chi $ Схема 1 З–Ш–З–Ш Схема 2 Ш–Ш–Ш–Ш Схема 3 Ш–С–Ш–С
ω* $k_{\xi }^{*}$ $T_{\xi }^{*}$ ω* $k_{\xi }^{*}$ $T_{\xi }^{*}$ ω* $k_{\xi }^{*}$ $T_{\xi }^{*}$
град Гц – кН/м Гц – кН/м Гц – кН/м
0 7.26 8.90 8.30 5.56 6.13 5.72 4.61 0.82 0.77
5 7.23 8.84 8.29 5.54 6.09 5.76 4.68 0.83 0.79
10 7.25 8.68 8.50 5.55 5.98 5.86 4.75 0.82 0.81
15 7.34 8.48 8.99 5.60 5.83 6.18 4.69 0.80 0.85
20 7.44 8.26 9.81 5.69 5.68 6.74 4.63 0.77 0.92
25 7.70 8.09 11.03 5.84 5.57 7.60 4.56 0.74 1.00
30 8.01 7.94 12.79 6.05 5.53 8.91 4.51 0.70 1.13
40 8.97 7.55 18.33 6.71 5.76 13.91 4.49 0.65 1.57
45 9.69 7.39 22.80 7.19 5.64 17.41 4.55 0.64 1.97
50 10.63 7.36 30.08 7.84 5.57 22.78 4.65 0.64 2.60

Наиболее низкие показатели соответствуют закреплению пластины по схеме 3 с двумя свободными кромками. Угол скоса сторон панели также существенно влияет на величину критической нагрузки сжатия, которая при углах $\chi $ > 45° в 3.4–4.0 раза превосходит критические значения для прямоугольных конструкций.

Далее проведем оценку влияния нагрузки сжатия в осевом направлении, действующей на контуре панели в осевом направлении, на собственные частоты колебаний панели. Для этого будем дискретно в долях критического усилия сжатия варьировать значения продольной нагрузки в виде

(8)
${{N}_{\xi }} = \pm \psi T_{\xi }^{*}\quad \left( {\psi = 0.3...0.6} \right).$

Подставляя (8) в систему (5) и преобразуя однородную систему к безразмерному виду

$\left( {[\Omega *] \mp \psi k_{\xi }^{*}\left[ {{{\Upsilon }_{\xi }}} \right] - \left\lfloor {{{\varsigma }^{2}}} \right\rfloor \left[ {\rm E} \right]} \right)\left\lfloor A \right\rfloor = 0,$
получим условие существования нетривиального решения в детерминантной форме

$\det \left( {[\Omega *] \mp \psi k_{\xi }^{*}\left[ {{{\Upsilon }_{\xi }}} \right] - \left\lfloor {{{\varsigma }^{2}}} \right\rfloor \left[ {\rm E} \right]} \right) = 0.$

Расчетные значения собственных частот колебаний косоугольных панелей из углепластика представлены на рис. 5 в виде графиков параметрических зависимостей нормированной частотной характеристики от угла скоса для трех исследованных вариантов закрепления. Показаны тренды изменения собственной частоты для четырех уровней продольного усилия сжатия для областей докритического устойчивого равновесия (два уровня) и закритического деформирования (два уровня) в сравнении с частотой $\omega _{{}}^{*}$ при нагружении критическим уровнем сжимающей силы. Повышение усилия сжатия на всем интервале докритического и закритического нагружения приводит к возрастанию собственных частот конструкции для всех условий закрепления краев панели.

Рис. 5.

Параметрические зависимости нормированной частотной характеристики $\omega {\text{/}}\omega {\kern 1pt} *$ от угла скоса $\chi $ для различных вариантов закрепления: (а) – схема 1; (б) – схема 2; (в) – схема 3; 1 – $\omega {\text{/}}\omega {\kern 1pt} *$ = 0.4; 2 – $\omega {\text{/}}\omega {\kern 1pt} *$ = 0.7; 3 – $\omega {\text{/}}\omega {\kern 1pt} *$ = 1.0; 4 – $\omega {\text{/}}\omega {\kern 1pt} *$ = 1.4; 5 – $\omega {\text{/}}\omega {\kern 1pt} *$ = 1.7.

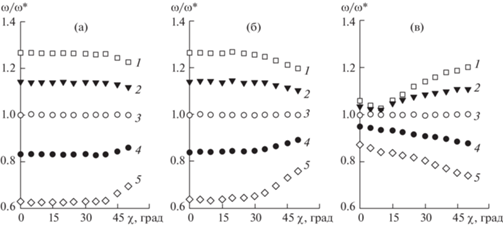
Для схем закрепления без свободных кромок (схемы 1 и 2) установлено отсутствие влияния скошенной формы c углами $\chi $ < 40° на отношение собственных частот докритического и закритического интервалов нагрузок к частоте $\omega {\kern 1pt} *$, соответствующей критической нагрузке. Значимое влияние угла скоса на частотные характеристики проявляется лишь для больших значений χ > 40–45°, при этом докритические нагрузки увеличивают значение собственной частоты панели, тогда как закритический уровень нагружения приводит к ее снижению. Для схемы закрепления с двумя шарнирно опертыми сторонами и двумя свободными (схема 3) влияние уровня осевой нагрузки носит иной характер – действие докритических уровней нагрузок приводит к уменьшению значений собственной частоты с ростом скошенности пластины, тогда как для нагрузок закритического уровня тенденция противоположная.

Выводы. 1. Динамический анализ косоугольных углепластиковых панелей показывает определяющую роль способа закрепления на частотные характеристики при свободных колебаниях системы. Эффективным в связи с этим следует признать использование в расчетной модели функций Крылова, позволяющих успешно описывать краевые эффекты в граничных областях пластины. 2. Для исследованных схем закрепления установлено, что при небольших отклонениях от прямоугольной формы пластины (угол скоса $\chi $ < 25°) влияние скошенности на динамический отклик конструкциии практически отсутствует. Для более жестких схем закрепления без свободных краев прогнозируется тенденция увеличения значений собственной частоты при больших углах скоса $\chi $ > 30°. 3. Важным фактором при динамическом анализе является нагружение осевым сжимающим усилием, определяющим устойчивость конструкции. Повышение усилия сжатия на всем интервале докритического и закритического нагружения приводит к возрастанию собственных частот конструкции для всех граничных условий на контуре.

Список литературы

  1. Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 272 с.

  2. Reddy J.N. Mechanics of laminated composite plates and shells. Theory and analysis, (2nd ed). New York: CRC Press, 2004. 831 p.

  3. Азиков Н.С., Зинин А.В., Гайдаржи Ю.В., Сайфуллин И.Ш. Прочность при закритическом деформировании косоугольных композиционных панелей // Проблемы машиностроения и надежности машин. 2021. № 5. С. 62.

  4. Азиков Н.С., Гайдаржи Ю.В. Устойчивость слоистых скошенных панелей // Механика композиционных материалов и конструкций. 2010. Т. 16. № 3. С. 361.

  5. Гайдаржи Ю.В., Азиков Н.С., Зинин А.В. Численное моделирование и анализ прочности и устойчивости вафельной оболочки // Проблемы машиностроения и автоматизации. 2021. № 2. С. 91.

  6. Бойцов Б.В., Гавва Л.М., Ендогур А.И., Фирсанов В.В. Напряженно-деформированное состояние и устойчивость конструктивно-анизотропных панелей летательных аппаратов из композиционных материалов с учетом технологии изготовления // Известия вузов. Авиационная техника. 2018. № 4. С. 20.

  7. Kiani Y. Free vibration of FG-CNT reinforced composite skew plates // Aerospace Science and Technology. 2016. V. 58. P. 130467-9 https://doi.org/10.1016/j.ast.2016.08.018

  8. Garg A.K. Free Vibration of Skew Fiber-reinforced Composite and Sandwich Laminates using a Shear Deformable Finite Element Model // J. of Sandwich Structures and Materials. 2006. V. 8 (1). P. 33. https://doi.org/10.1177/1099636206056457

  9. Azikov N.S., Zinin A.V. A Destruction Model for an Anisogrid Composite Structure // J. of Machinery Manufacture and Reliability. 2018. V. 47. № 5. P. 423.

  10. Фирсанов В.В., Фам В.Т., Чан Н.Д. Анализ напряженно-деформированного состояния многослойных композитных сферических оболочек на основе уточненной теории // Труды МАИ. 2020. № 14. С. 6.

  11. Гайдачук В.Е., Кириченко В.В., Кондратьев А.В., Сливинский В.И. и др. Расчет композитной панели солнечной батареи с сотовым заполнителем при различных случаях ее нагружения // В сб.: Материалы IV Международной конференции “Эффективность сотовых конструкций в изделиях авиационно-космической техники”. Днепропетровск, 2011. С. 40.

  12. Нуримбетов А.У., Дудченко А.А. Современное состояние вопроса анализа собственных частот и форм колебаний конструкции из композиционных материалов // Строительная механика инженерных конструкций и сооружений. 2018. Т. 14. № 4. С. 323. https://doi.org/10.22363/1815-5235-2018-14-4-323-336

  13. Васильев В.В. О преобразованиях Кирхгофа и Томсона–Тэта в классической теории пластин // Известия РАН. Механика твердого тела. 2012. № 5. С. 98.

  14. Elishakoff I., Hache F., Challamel N. Vibrations of asymptotically and variationally based Uflyand–Mindlin plate models // Int. J. of Engineering Science. 2017. V. 116. P. 58. https://doi.org/10.1016/j.ijengsci.2017.03.003

  15. Фирсанов В.В., Нгуен Л.Х. Анализ напряженно-деформированного состояния композиционных цилиндрических оболочек на основе уточненной теории с учетом пьезоэлектрического эффекта // Проблемы машиностроения и надежности машин. 2021. № 4. С. 37.

  16. Hou Y., Wel G.W., Xiang Y. DSC-Ritz method for the free vibration analysis of Mindlin plates // Int. J. for Numerical Methods in Engineering. 2004. V. 62 (2). P. 262. https://doi.org/10.1002/nme.1186

  17. Kumar R., Kumar A., Panda S.K. Parametric resonance of composite skew plate under non-uniform in-plane loading // Structural Engineering and Mechanics. 2015. V. 55. № 2. P. 435. https://doi.org/10.12989/sem.2015.55.2.435

  18. Haldar S., Pal S., Kalita K., Sagunthala R. Free vibration of skew laminates – a brief review and some benchmark results. Transactions of the Royal Institution of Naval Architects // Int. J. of Maritime Engineering. 2019. V. 161. Part A4. P. 357. https://doi.org/10.3940/nna.ijme.20I9.a4.540

  19. Adhikari B., Dash P. Geometrically nonlinear free vibration analysis of laminated composite plates: A finite element assessment of a higher order non-polynomial shear deformation theory // Mechanics of Advanced Materials and Structures. 2019. V. 28 (1). P. 1. https://doi.org/10.1080/15376494.2018.1553259

  20. Khan M., Kumar S. Smart damping of skew composite plates using Murakami zigzag function // SN Applied Sciences. 2021. V. 3 (4). https://doi.org/10.1007/S42452-021-04426-6

  21. Srinivasa C.V., Suresh Y.J., Prema Kumar W.P. Experimental and finite element studies on free vibration of skew plates // Int. J. of Advanced Structural Engineering. 2014. V. 6. P. 48. https://doi.org/10.1007/s40091-014-0048-3

  22. Zhou L., Zhen W.X. Vibration of skew plates by the MLS-Ritz method // Int. J. of Mechanical Sciences. 2008. V. 50 (7). P. 1133. https://doi.org/10.1016/j.ijmecsci.2008.05.002

  23. Xiang Y., Lai S. K., Zhou L., Lim C. W. DSC-Ritz element method for vibration analysis of rectangular Mindlin plates with mixed edge supports // European J. of Mechanics, A/Solids. 2010. V. 29 (4). P. 619. https://doi.org/10.1016/j.euromechsol.2009.12.007

  24. Sai Vivek K. Free Vibration of Skew Laminated Composite Plates with Circular Cutout by Finite Element Method // Int. J. of Modern Engineering Research. 2016. V. 6. Iss. 6. P. 15.

  25. Gürses M., Civalek Ö., Korkmaz A.K., Ersoy H. Free vibration analysis of symmetric laminated skew plates by discrete singular convolution technique based on first-order shear deformation theory // Int. J. for Numerical Methods in Engineering. 2009. V. 79 (3). P. 290. https://doi.org/10.1002/nme.2553

  26. Ferreira A.J.M., Roque C.M.C., Jorge R.M.N. Free vibration analysis of symmetric laminated composite plates by FSDT and radial basis functions // Computer methods in applied mechanics and engineering. 2005. V. 194 (39–41). P. 4265. https://doi.org/10.1016/j.cma.2004.11.0041

  27. Kiani Y. Free vibration of FG-CNT reinforced composite skew plates // Aerospace Science and Technology. 2016. V. 58. P. 130467-9. https://doi.org/10.1016/j.ast.2016.08.018

  28. Ashour A.S. The free vibration of symmetrically angle-ply laminated fully clamped skew plates // J. of Sound and Vibration. 2009. V. 323 (1–2). P. 444. https://doi.org/10.1016/j.jsv.2008.12.027

  29. Thai H., Kim S. Free vibration of laminated composite plates using two variable refined plate theory // Int. J. of Mechanical Sciences. 2010. V. 52. P. 626.

  30. Malekzadeh P. A differential quadrature nonlinear free vibration analysis of laminated composite skew thin plates // J. of Thin-Walled Structures. 2007. V. 45 (2). P. 237.

  31. Rashed J., Peyman Y., Shahrokh H. Stacking Sequence Optimization of Laminated Composite Plates for Free Vibration using Genetic Algorithm and Neural Networks // Int. Conf. on Advances in Mechanical Engineering – ICAME'15At, 2015, Istanbul, Turkey. https://doi.org/10.13140/rg.2.1.4124.0402

  32. Farsadi T., Asadi D., Kurtaran H. Fundamental frequency optimization of variable stiffness composite skew plates // Acta Mechanica. 2021. V. 232. P. 555. https://doi.org/10.1007/s00707-020-02871-9

  33. Kalita K., Dey P., Haldar S., Gao X.-Z. Optimizing frequencies of skew composite laminates with metaheuristic algorithms // Engineering with Computers. 2020. V. 36. P. 741. https://doi.org/10.1007/s00366-019-00728-x

  34. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984. 320 с.

  35. Шуп Т. Решение инженерных задач на ЭВМ: Практическое руководство. Пер. с англ. М.: Мир, 1982. 237 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал