1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2022

Проблемы машиностроения и надежности машин, 2022, № 5, стр. 43-52

Использование двухпараметрического критерия для прогнозирования траектории роста сквозной трещины в сжатом диске

А. М. Покровский 1, *, Ю. Г. Матвиенко 2, М. П. Егранов 1

1 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

2 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

* E-mail: pokrovsky@bmstu.ru

Поступила в редакцию 10.02.2022
После доработки 20.05.2022
Принята к публикации 21.06.2022

Полный текст (PDF)

Аннотация

В настоящее время оценка прочности и живучести конструкций с трещинами представляет собой актуальный вопрос современной механики разрушения, прогнозирование траектории трещины – одна из задач такого анализа. В настоящей работе на примере диаметрально сжимаемого круглого диска со сквозной центральной трещиной (бразильского диска) из полиметилметакрилата решена задача прогнозирования траектории магистральной трещины с помощью критерия максимальных тангенциальных напряжений в двух постановках. Показано, что учет Т-напряжений в двухпараметрическом критерии повышает точность моделирования траектории роста трещины, по сравнению с однопараметрическим критерием. Получены результаты значения угла страгивания трещины с использованием аналитических формул и численного моделирования методом конечных элементов. Проведена верификация полученных результатов расчетов посредством сравнения с экспериментальными данными.

Ключевые слова: механика разрушения, коэффициент интенсивности напряжений, Т-напряжения, бразильский диск, двухпараметрический критерий разрушения, траектория трещины, трещина обобщенного нормального отрыва

Распространение трещин является критически важным вопросом в инженерной практике из-за его сильного влияния на качество и работоспособность конструкций. Зачастую поле напряжений в ответственных элементах конструкций неоднородно, поэтому построение траектории трещины при смешанном нагружении является актуальной задачей современной механики разрушения.

В настоящее время предложен и широко используется целый ряд критериев разрушения. Эрдоган (Erdogan) и Си (Sih) предложили критерий максимальных тангенциальных напряжений (МТН) [1], Хусейн (Hussain) и соавторы – критерий максимальной скорости высвобождения упругой энергии деформации [2], Си – критерий минимума плотности энергии деформации [3]. Физическое обоснование критериев различно и область их применения может варьироваться в зависимости от материала, вида конструкции или детали. Локальные критерии позволяют получить направление роста трещины в малой окрестности около вершины трещины, полную траекторию можно построить с помощью итерационных алгоритмов.

Несмотря на то, что результаты, полученные с помощью описанных критериев, в основном, хорошо соотносятся с экспериментальными данными, все равно остается ряд задач, в которых наблюдаются значительные расхождения между теоретическими и экспериментальными данными. Одной из причин этого расхождения является использование только сингулярных членов в разложении функции напряжений в окрестности вершины трещины. Вильямс (Williams) [4] предложил разложение, в которое кроме сингулярных членов входит несингулярный член, называемый Т-напряжениями, которые лежат в плоскости трещины и не зависят от расстояния до ее вершины.

Вильямс и Эвинг (Ewing) впервые предложили критерий максимальных тангенциальных напряжений с учетом КИН и Т-напряжений в задаче о наклонной трещине в пластине [5]. Позднее Смит (Smith) и соавторы развили этот подход и представили обобщенный критерий максимальных тангенциальных напряжений [6]. Они показали, что учет Т-напряжений оказывает существенное влияние на начальный угол роста трещины и момент начала разрушения. Значительный вклад в изучение влияния Т‑напряжений на трещиностойкость разных материалов и конструкций внесли Аятоллахи (Ayatollahi), Алиха (Aliha) и другие авторы [7–9]. Подобным образом развиваются и энергетические критерии [10, 11].

Влияние Т-напряжений на трещиностойкость в последнее время исследуются все активнее. Здесь, в первую очередь, необходимо отметить развиваемую в работах [12–16] двухпараметрическую механику разрушения. Обстоятельный обзор и обобщение полученных результатов по изучению Т-напряжений приведены в монографии [12] и статье [17].

Целью настоящей статьи является сопоставление однопараметрического и двухпараметрического критерия МТН на примере задачи по моделированию траектории роста трещины обобщенного нормального отрыва в бразильском диске.

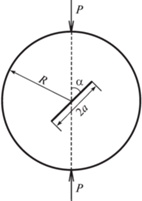
Постановка задачи. Одним из образцов для определения механических характеристик хрупких материалов является бразильский диск (БД) – диаметрально сжимаемая круглая пластинка со сквозной центральной трещиной (рис. 1).

Рис. 1.

Схема бразильского диска.

Особенностью БД является тот факт, что при изменении относительной длины трещины ${{\rho }} = \frac{a}{R}$ и угла ее наклона к линии действия сжимающей силы $F$, можно получить любую смешанность нагружения – от нормального отрыва до поперечного сдвига.

В статье рассматриваются результаты испытаний серии образцов со следующими геометрическими характеристиками: радиус диска $R = 40$ мм, полудлина трещины $a = 10$ мм, толщина диска $t = 4$ мм, угол наклона трещины $\alpha $ ∈ [0°, 7°, 15°, 22°, 30°, 45°, 60°, 75°].

Материал диска – полиметилметакрилат (ПММА), его механические характеристики: модуль упругости $E = 3000$ МПа, предел прочности при сжатии ${{\sigma }_{B}} = 70$ МПа, вязкость разрушения ${{K}_{{{\text{I}}c}}} = 40$ ${\text{МПа}}\sqrt {{\text{мм}}} $.

Формулировка критериев МТН. Вначале остановимся на однопараметрическом методе. При использовании разложения Вестергарда для описания напряженного состояния у вершины трещины угол страгивания θ* можно вычислить по формуле [18]

(1)
$\theta * = 2\operatorname{arctg} \left( {\frac{{1 - \sqrt {1 + 8{{\lambda }^{2}}} \operatorname{sign} \left( {{{K}_{{\text{I}}}}} \right)}}{{4\lambda }}} \right),$
где $~{{\lambda }} = {{K}_{{\text{I}}}}{\text{/}}{{K}_{{{\text{II}}}}}$; ${{K}_{{\text{I}}}}$, ${{K}_{{{\text{II}}}}}$ – коэффициенты интенсивности напряжений (КИН) I и II типов.

Выражение для тангенциальных напряжений в полярной системе координат имеет вид [4]

(2)
${{\sigma }_{\theta }}\left( {r,\theta } \right) = \frac{1}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left[ {{{K}_{{\text{I}}}}{{{\cos }}^{2}}\frac{\theta }{2} - \frac{3}{2}{{K}_{{{\text{II}}}}}\sin \theta } \right],$
где $r$ – радиус-вектор, проведенный из вершины трещины; ${{\theta }}$ – угол относительно оси, проходящей через плоскость трещины.

Вводя понятие эффективного КИН, и записывая формулу для тангенциальных напряжений в виде

${{\sigma }_{\theta }}\left( {r,\theta } \right) = \frac{{{{K}_{{\text{э}}}}}}{{\sqrt {2\pi r} }},$
можно получить выражение для эффективного КИН

${{K}_{{\text{э}}}} = \cos \frac{{\theta {\kern 1pt} *}}{2}\left[ {{{K}_{{\text{I}}}}{{{\cos }}^{2}}\frac{{\theta {\kern 1pt} *}}{2} - \frac{3}{2}{{K}_{{{\text{II}}}}}\sin \theta {\kern 1pt} *} \right].$

Приравнивая, согласно силовому критерию разрушения Ирвина эффективный КИН вязкости разрушения ${{K}_{{{\text{I}}c}}}$, приходим к условию разрушения

(3)
${{K}_{{\text{э}}}} = \cos \frac{{\theta {\kern 1pt} *}}{2}\left[ {{{K}_{{\text{I}}}}{{{\cos }}^{2}}\frac{{\theta {\kern 1pt} *}}{2} - \frac{3}{2}{{K}_{{{\text{II}}}}}\sin \theta {\kern 1pt} *} \right] = {{K}_{{{\text{I}}с}}}.$

Далее рассмотрим двухпараметрический метод. В этом случае для описания напряженного состояния у вершины трещины используют разложение Вильямса

${{\sigma }_{{ij}}}\left( {r,\theta } \right) = \mathop \sum \limits_{n = 1}^\infty \frac{n}{2}{{A}_{n}}{{r}^{{\frac{n}{2} - 1}}}f_{{A,ij}}^{{(n)}}\left( \theta \right) - \mathop \sum \limits_{n = 1}^\infty \frac{n}{2}{{B}_{n}}{{r}^{{\frac{n}{2} - 1}}}f_{{B,ij}}^{{(n)}}\left( \theta \right),$
где ${{A}_{n}}$, ${{B}_{n}}$ – амплитудные, масштабные коэффициенты, зависящие от геометрии образца с трещиной, а также от нагрузки; $f_{{A,ij}}^{{\left( n \right)}}\left( {{\theta }} \right)$, $f_{{B,ij}}^{{\left( n \right)}}\left( {{\theta }} \right)$ – тригонометрические функции угла ${{\theta }}$, определяемые из решения краевых задач о нормальном отрыве и поперечном сдвиге.

Коэффициенты при сингулярных членах в разложении Вильямса связаны с КИН следующими соотношениями

$\begin{gathered} \begin{array}{*{20}{c}} {{{K}_{{\text{I}}}} = \sqrt {2{{\pi }}} {{A}_{1}},~} \end{array} \\ {{K}_{{{\text{II}}}}} = - \sqrt {2{{\pi }}} {{B}_{1}}. \\ \end{gathered} $

Первый несингулярный член разложения – Т-напряжения определяется выражением

$\begin{array}{*{20}{c}} {T = 4{{A}_{2}}.} \end{array}$

Запишем формулу для тангенциальных напряжений в вершине трещины, удерживая два первых слагаемых [12]

(4)
${{\sigma }_{\theta }}\left( {r,\theta } \right) = \frac{1}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left[ {{{K}_{{\text{I}}}}{{{\cos }}^{2}}\frac{\theta }{2} - \frac{3}{2}{{K}_{{{\text{II}}}}}\sin \theta } \right] + T{{\sin }^{2}}\theta .$

Согласно критерию МТН, трещина распространяется вдоль линии действия максимальных растягивающих тангенциальных напряжений, поэтому

(5)
${{\left. {\frac{{\partial {{\sigma }_{\theta }}}}{{\partial \theta }}} \right|}_{{\theta = \theta *}}} = 0.$

Подставляя формулу (4) в условие (5), и заменяя r на rc, получаем уравнение для вычисления угла страгивания трещины $\theta {\kern 1pt} *$

(6)
${{K}_{{\text{I}}}}\sin \theta {\kern 1pt} * + \;{{K}_{{{\text{II}}}}}\left( {3\cos \theta {\kern 1pt} * - \;1} \right) - \frac{{16}}{3}T\sqrt {2\pi {{r}_{c}}} \sin \frac{{\theta {\kern 1pt} *}}{2}\cos \theta * = 0,$
где ${{r}_{c}} = \frac{1}{{2{{\pi }}}}{{\left( {\frac{{{{K}_{{{\text{I}}c}}}}}{{{{{{\sigma }}}_{0}}}}} \right)}^{2}}$ – размер зоны предразрушения [19]; ${{{{\sigma }}}_{0}}$ – локальная прочность в зоне предразрушения, для хрупких материалов – предел прочности.

Двухпараметрическое условие разрушения получаем аналогично тому, как это было сделано в однопараметрическом подходе. Отличие заключается лишь в выражении для тангенциальных напряжений. Условие разрушения, в который входит эффективный КИН будет выглядеть следующим

(7)
${{K}_{{\text{э}}}} = \cos \frac{{\theta {\kern 1pt} *}}{2}\left[ {{{K}_{{\text{I}}}}{{{\cos }}^{2}}\frac{{\theta {\kern 1pt} *}}{2} - \frac{3}{2}{{K}_{{{\text{II}}}}}\sin \theta {\kern 1pt} *} \right] + T\sqrt {2\pi {{r}_{c}}} {{\sin }^{2}}\theta * = {{K}_{{{\text{I}}c}}}.$

Подставляя в уравнение (7) размер зоны предразрушения, и принимая локальную прочность материала за предел прочности, окончательно получим условие разрушения в следующем виде

(8)
$\cos \frac{{\theta {\kern 1pt} *}}{2}\left[ {{{K}_{{\text{I}}}}{{{\cos }}^{2}}\frac{{\theta {\kern 1pt} *}}{2} - \frac{3}{2}{{K}_{{{\text{II}}}}}\sin \theta {\kern 1pt} *} \right] + T\frac{{{{K}_{{{\text{I}}с}}}}}{{{{\sigma }_{{\text{в}}}}}}{{\sin }^{2}}\theta * = {{K}_{{{\text{I}}c}}}.$

Таким образом, в двухпараметрическое условие разрушения, кроме ${{K}_{{\text{I}}}}$, ${{K}_{{{\text{II}}}}}$ и ${{K}_{{{\text{I}}c}}}$ входят еще и Т-напряжения и предел прочности. Для моделирования траектории распространения трещины при использовании однопараметрического МТН необходимо вычислять КИН первого и второго типов для каждого шага продвижения трещины, а при использовании двухпараметрического МТН еще и Т-напряжения.

Расчет параметров механики разрушения. КИН и Т-напряжения можно определить численно с помощью МКЭ или с помощью аналитических соотношений. Аткинсон получил уравнения для нахождения ${{K}_{{\text{I}}}}$ и ${{K}_{{{\text{II}}}}}$ в бразильском диске [20],

(9)
$\begin{gathered} {{K}_{{\text{I}}}} = \frac{P}{{\pi Rt}}\sqrt {\pi a} \,\mathop \sum \limits_{i = 1}^n \,{{T}_{i}}{{\left( {\frac{a}{R}} \right)}^{{2i - 2}}}{{A}_{i}}\left( \theta \right), \\ {{K}_{{{\text{II}}}}} = - 2\frac{P}{{\pi Rt}}\sqrt {\pi a} \sin 2\theta \,\mathop \sum \limits_{i = 1}^n \,{{S}_{i}}{{\left( {\frac{a}{R}} \right)}^{{2i - 2}}}{{B}_{i}}\left( \theta \right), \\ \end{gathered} $
где ${{T}_{i}}\left( {\frac{a}{R}} \right)$, ${{S}_{i}}\left( {\frac{a}{R}} \right)$ – функции относительной длины трещины; ${{A}_{i}}\left( \theta \right)$, ${{B}_{i}}\left( \theta \right)$ – функции угловой координаты; $i$ – число удерживаемых членов ряда.

Соотношение для определения Т-напряжений в бразильском диске получено авторами [21, 22]

(10)
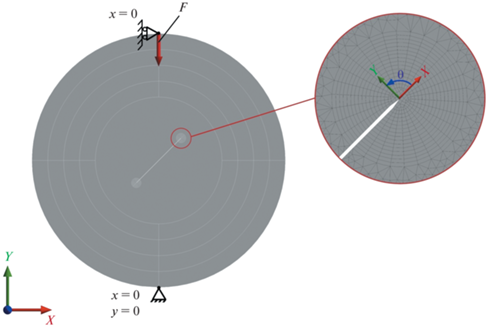
$T = \frac{P}{{\pi Rt}}{{f}_{1}} + 2\frac{P}{{\pi Rt}}\mathop \sum \limits_{i = 1}^n \left( {{{C}_{i}}\left( \theta \right){{f}_{i}} - {{C}_{i}}\left( \theta \right) - {{D}_{i}}\left( \theta \right)} \right){{\left( {\frac{a}{R}} \right)}^{{2\left( {i - 1} \right)}}},$
где ${{f}_{i}}$ – постоянные в разложении; ${{C}_{i}}\left( \theta \right)$, ${{D}_{i}}\left( \theta \right)$ – функции угловой координаты.

При продвижении трещины, она становится не прямолинейной, и аналитические методы расчета КИН и Т-напряжений становятся непригодными. Поэтому при моделировании траектории распространения трещины КИН и Т-напряжения вычислялись с помощью встроенной функции, основанной на вычислении М-интеграла в программном комплексе ANSYS Workbench. Расчетная модель состояла из 20614 8-узловых плоских элементов (рис. 2). На рис. 3 приведено сравнение КИН и Т-напряжений, полученных по аналитическим формулам (9), (10) и численно с помощью МКЭ для исходной трещины при внешней нагрузке ${{F}_{1}} = 1$ H.

Рис. 2.

Расчетная КЭ-модель.

Рис. 3.

Значение КИН (а) Т-напряжений (б), рассчитанные по аналитическим формулам и численно с помощью МКЭ.

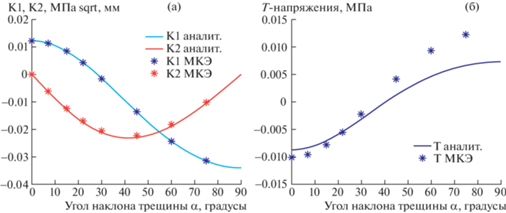
Значение КИН (рис. 3), рассчитанное численно и аналитически, хорошо совпадают. Т-напряжения различаются значительно для углов наклона трещины $\theta > 28^\circ $. Как видно из рисунка именно при этом угле наклона трещины значение ${{K}_{{\text{I}}}}$ становится отрицательным, а при отрицательных значениях ${{K}_{{\text{I}}}}$, как отмечено в работе [20], аналитическое решение (10) не справедливо.

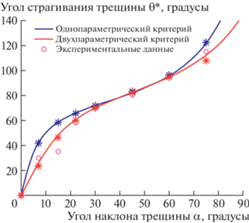
Расчет угла страгивания трещины и разрушающей нагрузки. С помощью уравнений (1) и (6) определены углы страгивания трещины θ* при использовании аналитического и численного расчета КИН и Т-напряжений. Сравнение полученных результатов с экспериментальными данными приведено на рис. 4. Как видно из рисунка двухпараметрический критерий дает немного лучшие результаты по сравнению с экспериментальными данными.

Рис. 4.

Сравнение углов страгивания трещины θ*, град.

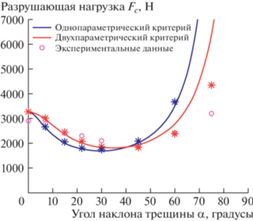
Разрушающая нагрузка вычисляется на основе значений КИН и Т-напряжений, полученных с помощью аналитических соотношений и численного расчета МКЭ. Эффективный КИН определяется по уравнениям (3) и (7). Ввиду линейности рассматриваемой задачи, разрушающую нагрузку можно вычислить с помощью следующего уравнения

${{F}_{c}} = {{F}_{1}}\frac{{{{K}_{{{\text{I}}c}}}}}{{{{K}_{{\text{э}}}}}}.$

Сравнение полученных результатов с экспериментальными данными приведено на рис. 5.

Рис. 5.

Сравнение значений разрушающей нагрузки ${{F}_{c}}$, H.

Моделирование траектории трещины. Моделирование траектории трещины проводилось с использованием шагового алгоритма, который заключается в следующем: 1) создается конечно-элементная модель диска с исходной трещиной; 2) для этой трещины вычисляются KI, KII и Т-напряжения и определяется угол, характеризующий направление роста трещины относительно исходной ориентации, по формулам (1) для однопараметрического критерия и (6) для двухпараметрического; 3) под этим углом трещина продлевается на заданный шаг, который вычисляется в процессе численного эксперимента. Создается конечно-элементная модель диска с подросшей трещиной; 4) все повторяется, начиная с п. 2. Моделирование продолжается пока трещина не пройдет через весь диск.

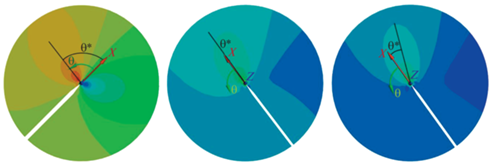
Распределение тангенциальных напряжений и угол распространения трещины вблизи ее вершины для трех шагов описанного алгоритма приведены на рис. 6.

Рис. 6.

Тангенциальные напряжения и угол распространения трещины.

Для выбора шага по длине трещины расчеты проводятся с разными шагами и сравнивается траектория. Если при уменьшении шага траектория не изменяется, значит можно использовать данный шаг.

В качестве иллюстрации работы разработанных программных средств на рис. 7 представлены траектории роста трещины в диске с углом наклона трещины ${{\alpha }} = 45^\circ $, полученные с различным шагом по длине трещины с помощью однопараметрического и двухпараметрического критериев МТН. В табл. 1 приведено изменение КИН, Т‑напряжений и угла θ* в процессе роста трещины для двухпараметрического критерия при шаге 3 мм, данные в столбцах А относятся к однопараметрическому критерию, а в столбцах Б – к двухпараметрическому.

Рис. 7.

Траектории роста трещины, полученные с помощью однопараметрического и двухпараметрического критериев МТН с шагом: 7 мм (а), 5 мм (б), 3 мм (в).

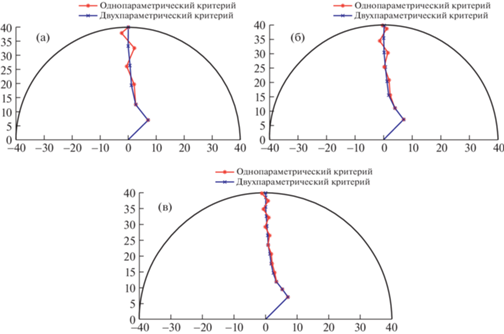
Таблица 1.

Изменение параметров механики разрушения для трещины с углом наклона $\theta = 45^\circ $ с шагом $l = 3$ мм

Шаг, № ${{K}_{{\text{I}}}}$, ${\text{МПа}}\sqrt {{\text{мм}}} $ ${{K}_{{{\text{II}}}}}$, ${\text{МПа}}\sqrt {{\text{мм}}} $ Т-напряжения, МПа ${{K}_{{\text{э}}}}$, ${\text{МПа}}\sqrt {{\text{мм}}} $ θ*, °
А Б А Б А А Б А Б
1 –28.34 –24.94 –46.81 –41.19 7.64 40.29 40.26 82.3 83.3
2 46.13 40.46 0.59 1.46 –14.35 46.14 40.5 –1.5 –2.57
3 42.68 37.42 8.91 8.06 –12.7 45.29 39.03 –21.9 –15.1
4 47.67 40.96 –1.31 5.72 –18.2 47.72 41.63 3.2 –9.0
5 52.20 46.22 6.19 2.31 –22.64 53.28 46.31 –13.2 –3.1
6 59.45 52.48 –6.71 1.46 –27.23 60.56 52.51 12.6 –1.7
7 66.19 60.18 14.29 1.25 –31.93 70.49 60.20 –22.5 –1.2
8 74.78 69.60 –22.13 0.77 –38.64 83.44 69.61 28.8 –0.6
9 79.15 81.31 38.74 1.71 –48.53 100.8 81.34 –39.8 –1.2
10 87.13 97.06 –56.54 1.97 –63.81 124.1 97.09 45.6 –1.1
11 87.72 122.49 93.65 2.04 –96.23 163.3 122.5 –55.0 –0.9
12 53.02 196.88 –182.8 10.34 –256.81 241.4 193.1 65.0 –1.9

Оба критерия (рис. 7) позволяют получить схожую траекторию трещины. Тем не менее, при любом из рассмотренных шагов прироста трещины, траектория, построенная с помощью двухпараметрического критерия, учитывающего Т-напряжения, является более гладкой. Кроме того, из рисунка видно, что траектории, полученные по двухпараметрическому критерию МТН для шагов 3 и 5 мм практически не отличаются, что свидетельствует об адекватном моделировании траектории, начиная с шага, равного 5 мм.

На рис. 8 представлено сравнение численного моделирования траектории роста трещины с использованием двухпараметрического критерия с данными эксперимента. Из рисунка видно, что численные результаты хорошо согласуются с экспериментальными данными.

Рис. 8.

Сравнение смоделированной и экспериментальной траектории трещины, угол α = 45°.

Заключение. В настоящей статье с помощью двух формулировок критерия максимальных тангенциальных напряжений проведено моделирование разрушения бразильского диска, определены разрушающая нагрузка, угол страгивания трещины и траектория трещины, достоверность полученных результатов подтверждена сравнением с данными эксперимента. В результате проведенного исследования можно сформулировать следующие выводы: 1. Учет Т-напряжений в критерии разрушения позволяет получить более точное значение угла страгивания трещины и разрушающей нагрузки. 2. Траектория трещины обобщенного нормального отрыва, построенная с учетом Т-напряжений является более гладкой и лучше совпадает с экспериментальной.

Список литературы

  1. Erdogan F., Sih G.C. On the Crack Extension in Plates under Plane Loading and Transverse Shear // J. of Basic Engineering. 1963. V. 85 (4). P. 519.

  2. Hussain M.A., Pu S.L., Underwood J. Strain Energy Release Rate for a Crack Under Combined Mode I and Mode II // Proceedings of the 1973 National Symposium on Fracture Mechanics, Maryland, 27–29 August, 1973. P. 2.

  3. Sih G.C. Strain-energy-density factor applied to mixed mode crack problems // Int. J. of Fracture. 1974. V. 10 (3). P. 305.

  4. Williams M.L. On the Stress Distribution at the Base of a Stationary Crack // J. of Applied Mechanics. 1957. V. 24 (1). P. 109.

  5. Williams J.G., Ewing P.D. Fracture under complex stress – the angled crack problem // Int. J. of Fracture. 1972. V. 26 (8). P. 441.

  6. Smith D.J., Ayatollahi M.R., Pavier M.J. The role of  T-stress in brittle fracture for linear elastic materials under mixed-mode loading // Fatigue & Fracture of Engineering Materials & Structures. 2001. V. 24 (2). P. 137.

  7. Ayatollahi M.R., Aliha M.R.M. On determination of mode II fracture toughness using semi-circular bend specimen // Int. J. of Solids and Structures. 2006. V. 43 (17). P. 5217.

  8. Ayatollahi M.R., Aliha M.R.M. Mixed mode fracture in soda lime glass analyzed by using the generalized MTS criterion // Int. J. of Solids and Structures. 2009. V. 46 (2). P. 311.

  9. Saghafi H., Ayatollahi M.R., Sistaninia M. A modified MTS criterion for mixed mode fracture toughness assessment of brittle materials // Material Science and Engineering A. 2010. V. 527 (21). P. 5624.

  10. Ayatollahi M.R., Rashidi Moghaddam M., Berto F. A generalized strain energy density criterion for mixed mode fracture analysis in brittle and quasi-brittle materials // Theoretical and Applied Fracture Mechanics. 2015. V. 79. P. 70.

  11. Ayatollahi M.R., Rashidi Moghaddam M., Razavi S.M.J., Berto F. Mode I fracture analysis of PMMA using modified energy-based models // Physical Mesomechanics. 2015. V. 18 (4). P. 13.

  12. Матвиенко Ю.Г. Двухпараметрическая механика разрушения. М.: ФИЗМАТЛИТ, 2020. 208 с.

  13. Матвиенко Ю.Г. Двухпараметрическая механика разрушения в современных проблемах прочности // Проблемы машиностроения и надёжности машин. 2013. № 5. С. 37.

  14. Степанова Л.В. Влияние высших приближений в асимптотическом разложении М. Уильямса поля напряжений на описание напряжённо-деформированного состояния у вершины трещины. Часть I // Вестник Самарского университета. Естественнонаучная серия. 2019. Т. 25. № 1. С. 63.

  15. Степанова Л.В. Влияние высших приближений в асимптотическом разложении М. Уильямса поля напряжений на описание напряжённо-деформированного состояния у вершины трещины. Часть II // Вестник Самарского университета. Естественнонаучная серия. 2019. Т. 25. № 1. С. 80.

  16. Степанова Л.В., Росляков П.С. Многопараметрический анализ поля напряжений у вершины трещины // Вестник Самарского университета. Естественнонаучная серия. 2015. Т. 10. № 132. С. 52.

  17. Gupta M., Alderliesten R.C., Benedictus R. A review of T-stress and its effects in fracture mechanics // Engineering Fracture Mechanics. 2014. V. 132. P. 218.

  18. Панасюк В.В. Предельное равновесие хрупких тел с трещинами. Киев: Наукова думка, 1968. 246 с.

  19. Schmidt R.A. A microcrack and its significance to hydraulic fracturing and fracture toughness testing // Proceedings 21st US Symposium on Rock Mechanics, Rolla, Missouri, 28–30 May 1980. P. 581.

  20. Atkinson C., Smelser R.E., Sanchez J. Combined mode fracture via the cracked Brazilian disc test // Int. J. of Fracture. 1982. V. 18. P. 279.

  21. Fett T. Stress intensity factors and T-stress for internally cracked circular disks under various boundary conditions // Engineering Fracture Mechanics. 2001. V. 68 (9). P. 1119.

  22. Hua W., Li Y., Dong S., Li N., Wang Q. T-stress for a centrally cracked Brazilian disc under confining pressure // Engineering Fracture Mechanics. 2015. V. 149 (11). P. 37.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал