Проблемы машиностроения и надежности машин, 2022, № 6, стр. 21-30

Механические напряжения в многослойных осесимметричных магнитных и токовых системах

А. К. Андреев^*

Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

Поступила в редакцию 16.03.2022
После доработки 11.08.2022
Принята к публикации 19.08.2022

EDN: RAKEUW
DOI: 10.31857/S0235711922060037

Аннотация

Предложен метод расчета радиальных и аксиальных механических напряжений в многослойных магнитных и токовых системах с произвольными расстояниями между слоями. Напряжения вычисляются из энергии аксиально намагниченных цилиндров. Приведены расчетные формулы 3D-полей и размагничивающих факторов цилиндров, выраженные через функции Бесселя. Представлены тестовые результаты расчетов напряжений и, как дополнение, взаимных индуктивностей системы катушек и индуктивностей отдельных слоев.

Ключевые слова: механические напряжения, размагничивающий фактор, межслойные напряжения, функции Бесселя, пондеромоторные силы, индуктивность

Расчет пондеромоторных сил в магнитных системах необходим при разработке различных устройств и механизмов в машиностроении и других областях. Выполненные ранее подобные расчеты связаны, в основном, с созданием импульсных магнитных полей высокой интенсивности. Работы [1–5] посвящены технической реализации поставленных задач с акцентом на прочностные характеристики изделий. В расчетах используются приближенные формулы определения магнитных полей, полученные методами теоретической электротехники для токовых систем. Обычно рассчитываются интегральные напряжения обмотки по среднему витку.

В статье приведен альтернативный аналитический метод определения пондеромоторных сил и взаимной индуктивности сложных коаксиальных магнитных систем. Метод основан на модели аксиально намагниченного цилиндра и применим для катушек с плотной намоткой.

Катушка, цилиндр и связанные с ними системы координат показаны на рис. 1.

Рис 1.

Схема определения индукции катушки и цилиндра ${\mathbf{B}}$ – (а); Схема расчета поля цилиндра ${\mathbf{H}}$ – (б); $q\left( {r{\kern 1pt} ',z{\kern 1pt} '} \right)$ – точка источника поля; $a(r,z)$ – точка наблюдения. Начало координат расположено в торце систем.

В модели используется факт равенства внутренних энергий аксиально намагниченных цилиндров и геометрически эквивалентных им катушек. Этот метод использовался в работе [6] при расчете взаимных индуктивностей катушек и пондеромоторных сил при взаимном продольном смещении двух магнитных систем. В [6] приведены ссылки на публикации, содержащие детали теоретической модели, не представленные в настоящей статье.

Математическая модель. В расчетах используются формулы, связывающие намагниченность цилиндра ${{{\mathbf{M}}}_{z}}$ с плотностью поверхностного тока цилиндра ${{{\mathbf{j}}}_{{{\text{пов}}}}}$ и поверхностными “магнитными зарядами” [7]: ${{{\mathbf{j}}}_{{{\text{пов}}}}} = \operatorname{Rot} {{{\mathbf{M}}}_{z}}$, $\sigma = - \operatorname{Div} {{{\mathbf{M}}}_{z}}$. При однородной намагниченности (${{{\mathbf{M}}}_{z}} = {\text{const}}$) ${{{\mathbf{J}}}_{{{\text{пов}}}}} = \left[ {{{{\mathbf{M}}}_{z}}{\mathbf{n}}} \right]$ (рис. 1а), $\sigma = {{{\mathbf{M}}}_{z}}{\mathbf{n}}$ (рис. 1б), где ${\mathbf{n}}$ – внешняя нормаль к боковой и торцевым поверхностям цилиндра. В скалярной записи имеем соответственно

(1)

${{M}_{z}} = {{j}_{{{\text{пов}}}}},\quad \sigma = {{M}_{z}}.$

При заданных параметрах катушки: длине $L$, диаметре $2a$, числе витков $w$ и токе в витке $I$ плотность тока обмотки $j = wI{\text{/}}n$. Полагая ${{j}_{{{\text{пов}}}}} = j$ эквивалентная намагниченность равноразмерного цилиндра равна ${{M}_{z}} = j$ (рис. 1а), что обеспечивает равенство индукций катушки и цилиндра ${\mathbf{B}}$ во всем пространстве. При определенных выше условиях равноразмерная катушка эквивалентна цилиндру и далее токовая модель (катушка) в расчетах не используется.

Поля в объемах катушки и цилиндра радикально различаются. Согласно дипольной (“зарядовой”) модели намагниченности на торцах однородно намагниченного цилиндра возникают поверхностные “магнитные заряды” $ \pm \sigma $ (рис. 1б). “Заряды” создают размагничивающее поле ${{{\mathbf{H}}}_{p}}({\mathbf{r}})$ в объеме цилиндра, определяемое размагничивающим фактором формы образца $N({\mathbf{r}})$, и поле рассеяния вне его, обозначаемое также символом ${{{\mathbf{H}}}_{p}}$. Размагничивающее поле ${{{\mathbf{H}}}_{p}}({\mathbf{r}})$ связано с ${{{\mathbf{M}}}_{z}}$ через размагничивающий фактор $N({\mathbf{r}})$

(2)

${{{\mathbf{H}}}_{p}}({\mathbf{r}}) = - N({\mathbf{r}}) \cdot {{{\mathbf{M}}}_{z}}.$

Вне цилиндра ${{{\mathbf{M}}}_{z}} = 0$ и размагничивающее поле равно нулю ${{{\mathbf{H}}}_{p}} = 0$. Поле ${{{\mathbf{H}}}_{p}}$ терпит разрыв на торцах цилиндра. ${{{\mathbf{H}}}_{p}}$ и $N({\mathbf{r}})$ есть функции координат ${\mathbf{r}}$. Вне цилиндра $N(r)$ есть коэффициент пропорциональности между ${{{\mathbf{M}}}_{z}}$ и полем рассеяния. Поля ${{{\mathbf{H}}}_{p}}$ внутри и вне образца рассчитываются по единым аналитическим выражениям.

Индукция цилиндра ${\mathbf{B}}$ связана с ${{{\mathbf{H}}}_{p}}$ и ${{{\mathbf{M}}}_{z}}$ соотношением

(3)

${\mathbf{B}} = {{\mu }_{0}}\left( {{{{\mathbf{H}}}_{p}} + {{{\mathbf{M}}}_{z}}} \right),$

где ${{\mu }_{0}}$ – магнитная постоянная. На рис. 2 приведены графики векторного поля индукции $B$ и поля $H$ вдоль осевого сечения цилиндра.

Рис. 2.

График векторного поля индукции $B$ – (а); график векторного поля $H$ – (б). Внутренняя область магнитной системы в рамке затемнена.

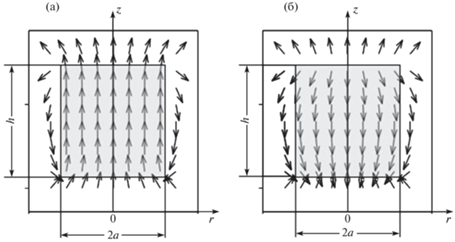
На рис. 3 построены графики изменения ${{B}_{z}}$ и ${{H}_{z}}$ цилиндра вдоль продольного Z ($r = 0$) и радиального r ($z = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$) направлений.

Рис. 3.

Графики изменения индукции ${{B}_{z}}$ и поля ${{H}_{z}}$ одиночного цилиндра с параметрами $a = 10$ см, $L = 20$ см, ${{M}_{z}} = 2.5 \times {{10}^{3}}$ А/м: (а) – вдоль оси Z; (б) – в радиальном направлении r по центру цилиндра ($z = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$).

Размагничивающий фактор аксиально намагниченного цилиндра. Расчет размагничивающего фактора $N$ и поля ${{H}_{p}}$ проводится с использованием модели однородно намагниченного в аксиальном направлении цилиндрического магнита. Для расчета $N$ используется “зарядовая модель” (рис. 1б). То есть, поле цилиндра рассчитывается как суперпозиция полей от торцевых поверхностей с поверхностными “магнитными зарядами” $ + \sigma $ и $ - \sigma $.

Схема определения потенциала отрицательно заряженного торца цилиндра в точке наблюдения $a(z,r)$ приведена на рис. 1б. Точка наблюдения может располагаться как в объеме образца, так и вне его. Магнитостатический потенциал в точке наблюдения определяемый намагниченностью равен [8]

(4)

$\varphi ({\mathbf{r}}) = \int\limits_{V'} {{\mathbf{M}}\left( {{\mathbf{r}}{\kern 1pt} '} \right)\nabla {\kern 1pt} '{\kern 1pt} \frac{1}{{\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '{\kern 1pt} } \right|}}} \;{{d}^{3}}{\mathbf{r}}{\kern 1pt} ',$

где ${\mathbf{r}}{\kern 1pt} '$ – радиус-вектор точки источника $q\left( {r{\kern 1pt} ',z{\kern 1pt} '} \right)$; ${\mathbf{r}}$ – радиус-вектор точки наблюдения $a(r,z)$. ${{d}^{3}}{\mathbf{r}}{\kern 1pt} '$ – означает элемент объема $V{\kern 1pt} '$. Формулы (4) определяют потенциал как внутри (в объеме) ферромагнетика, так и вне его. Поле внутри и вне ферромагнетика при известном распределении ${\mathbf{M}}({\mathbf{r}}{\kern 1pt} ')$ выражается через градиент потенциала (4) в точке наблюдения $a(z,r)$.

При однородной намагниченности ${{M}_{z}}$ вдоль оси $Z$ поля ${{H}_{p}}$ равны

(5)

${{H}_{p}}({\mathbf{r}}) = - \nabla \varphi (r) = - {{M}_{z}}\left[ {\nabla \int\limits_{V'} {\alpha \left( {{\mathbf{r}}{\kern 1pt} '} \right) \cdot \nabla {\kern 1pt} '{\kern 1pt} \frac{1}{{\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '{\kern 1pt} } \right|}}} dV{\kern 1pt} '} \right] = - {{M}_{z}}N({\mathbf{r}}),$

где $\alpha \left( {{\mathbf{r}}{\kern 1pt} '} \right) = {{\alpha }_{z}} = 1$ – единичный вектор направления намагниченности. Штрихованный и не штрихованный операторы означают дифференцирование по точкам источника $q\left( {r{\kern 1pt} ',z{\kern 1pt} '} \right)$ и наблюдения $a(r,z)$, соответственно. Выражение, заключенное в квадратные скобки, определяет размагничивающий фактор $N({\mathbf{r}})$. Компоненты поля ${{H}_{p}}$ можно определить следующим образом ${{H}_{i}} = - {{N}_{{iz}}}{{M}_{z}}$, $i = r,z$. Исключая ${{M}_{z}}$ из (5) можно записать следующий вспомогательный потенциал в цилиндрической системе координат:

(6)

${{\psi }_{1}}({\mathbf{r}}) = - \int\limits_0^a {r{\kern 1pt} '{\kern 1pt} dr{\kern 1pt} '{\kern 1pt} \int\limits_0^{2\pi } {d\theta {\kern 1pt} '\left[ \begin{gathered} \frac{1}{{\sqrt {{{r}^{2}} + r{{{_{{}}^{'}}}^{2}} + {{{\left( {L - z} \right)}}^{2}} - 2rr{\kern 1pt} '\cos \left( {\theta - \theta {\kern 1pt} '} \right)} }} \hfill \\ - \frac{1}{{\sqrt {{{r}^{2}} + r{\kern 1pt} {{'}^{2}} + {{z}^{2}} - 2rr{\kern 1pt} '\cos \left( {\theta - \theta {\kern 1pt} '} \right)} }} \hfill \\ \end{gathered} \right]} } \;0 \leqslant z \leqslant L \wedge \left| r \right| \leqslant a.$

Потенциалы (6) хорошо изучены и выражаются через специальные функции. Представление через функции Бесселя [9, 10] запишем как

(7)

${{\psi }_{1}}(r,z) = 2\pi a\int\limits_0^\infty {{{J}_{0}}(tr){{J}_{1}}(ta)\left[ {{{e}^{{ - tz}}} + {{e}^{{ - \left( {L - z} \right)}}}} \right]} \frac{{dt}}{t},\quad \left( {0 \leqslant z \leqslant L} \right) \wedge \left| r \right| \leqslant a,$

где ${{J}_{0}}(tr)$, ${{J}_{1}}(ta)$ – функции Бесселя нулевого и первого порядка от действительного аргумента. Применяя теорему Липшица и теорему сложения бесселевых функций получаем формулы для размагничивающих факторов [11]

(8)

$\begin{gathered} {{N}_{{zz}}}(r,z) = - \frac{\partial }{{\partial z}}{{\psi }_{1}}(r,z) = \frac{1}{2}a\int\limits_0^\infty {{{J}_{0}}(tr){{J}_{1}}(ta)\left[ {{{e}^{{ - tz}}} + {{e}^{{ - \left( {L - z} \right)}}}} \right]} dt,\quad 0 \leqslant z \leqslant L \wedge \left| r \right| \leqslant a, \\ {{N}_{{rz}}}(r,z) = - \frac{\partial }{{\partial r}}{{\psi }_{1}}(r,z) = - \frac{1}{2}a\int\limits_0^\infty {{{J}_{1}}(tr){{J}_{1}}(ta)\left[ {{{e}^{{ - tz}}} - {{e}^{{ - t\left( {L - z} \right)}}}} \right]} dt,\quad \left| r \right| \leqslant a. \\ \end{gathered} $

Для расчета полей удобно использовать координатную систему с началом координат в центре цилиндра. Размагничивающие коэффициенты для расчета 3D-полей внутри и вне цилиндра равны [6]

(9)

$\begin{gathered} {{N}_{{zz}}}\left( {n,r,z{\kern 1pt} '} \right) = \left| \begin{gathered} \frac{1}{2}a(n)\int\limits_0^\infty {{{J}_{0}}\left( {tr} \right){{J}_{1}}\left[ {ta(n)} \right]} \left[ {{{e}^{{ - tz'}}} + {{e}^{{ - t\left[ {L(n) - z'} \right]}}}} \right]dt,\quad {\text{если}}\quad \left[ {0 \leqslant z{\kern 1pt} ' \leqslant L(n)} \right], \hfill \\ \frac{1}{2}a(n)\int\limits_0^\infty {{{J}_{0}}\left( {tr} \right){{J}_{1}}\left[ {ta(n)} \right]} \left[ {{{e}^{{ - tz'}}} - {{e}^{{t\left[ {L(n) - z')} \right]}}}} \right]dt,\quad {\text{если}}\quad \left[ {z{\kern 1pt} ' \succ L(n)} \right], \hfill \\ \frac{1}{2}a(n)\int\limits_0^\infty {{{J}_{0}}\left( {tr} \right){{J}_{1}}\left[ {ta(n)} \right]} \left[ {{{e}^{{ - t\left[ {L(n) - z'} \right]}}} - {{e}^{{tz'}}}} \right]dt,\quad {\text{если}}\quad \left( {z{\kern 1pt} ' \prec 0} \right), \hfill \\ - \frac{1}{2}\left[ {\frac{{L(n) - z{\kern 1pt} '}}{{\sqrt {{{{\left[ {L(n) - z{\kern 1pt} '} \right]}}^{2}} + {{a}^{2}}} }} + \frac{{z{\kern 1pt} '}}{{\sqrt {z{\kern 1pt} {{'}^{2}} + {{a}^{2}}} }} - \frac{{L(n) - z{\kern 1pt} '}}{{\left| {L(n) - z{\kern 1pt} '} \right|}} - \frac{{z{\kern 1pt} '}}{{\left| {z{\kern 1pt} '} \right|}}} \right]\quad {\text{везде;}} \hfill \\ \end{gathered} \right. \hfill \\ {{N}_{{rz}}}\left( {n,r,z{\kern 1pt} '} \right) = \left| \begin{gathered} \frac{1}{2}a(n)\int\limits_0^\infty {{{J}_{0}}\left( {tr} \right){{J}_{1}}\left[ {ta(n} \right]} \left[ {{{e}^{{ - tz{\kern 1pt} '}}} + {{e}^{{ - t\left[ {L(n) - z{\kern 1pt} '} \right]}}}} \right]dt,\quad {\text{если}}\quad \left[ {0 \leqslant z{\kern 1pt} ' \leqslant L(n)} \right], \hfill \\ \frac{1}{2}a(n)\int\limits_0^\infty {{{J}_{0}}\left( {tr} \right){{J}_{1}}\left[ {ta(n)} \right]} \left[ {{{e}^{{ - tz{\kern 1pt} '}}} - {{e}^{{t\left[ {L(n) - z{\kern 1pt} '} \right]}}}} \right]dt,\quad {\text{если}}\quad \left[ {z{\kern 1pt} ' \succ L(n)} \right], \hfill \\ \frac{1}{2}a(n)\int\limits_0^\infty {{{J}_{0}}\left( {tr} \right){{J}_{1}}\left[ {ta(n)} \right]} \left[ {{{e}^{{ - t\left[ {L(n) - z{\kern 1pt} '} \right]}}} - {{e}^{{tz{\kern 1pt} '}}}} \right]dt,\quad {\text{если}}\quad \left( {z{\kern 1pt} ' \prec 0} \right), \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $

где $a(n)$, $L(n)$ – радиус и длина $n$-го цилиндра, соответственно; $z{\kern 1pt} '(z,n) = z + {{L(n)} \mathord{\left/ {\vphantom {{L(n)} 2}} \right. \kern-0em} 2}$; $Z$ и $r$ – компоненты полей определим как

(10)

${{H}_{z}}\left( {n,r,z{\kern 1pt} '} \right) = - {{M}_{z}}(n){{N}_{{zz}}}\left( {n,r,z{\kern 1pt} '} \right),\quad {{H}_{r}}\left( {n,r,z{\kern 1pt} '} \right) = - {{M}_{z}}(n){{N}_{{rz}}}\left( {n,r,z{\kern 1pt} '} \right).$

Поле ${{H}_{r}}$ перпендикулярно ${{M}_{z}}$, не вносит вклада в энергию, и в дальнейших расчетах не учитывается.

С учетом (2), (3), (10) получаем $Z$ компоненту индукции

(11)

${{B}_{z}}\left( {n,r,z{\kern 1pt} '} \right) = \left| \begin{gathered} {{\mu }_{0}}{{M}_{z}}(n)\left[ {1 - {{N}_{{zz}}}\left( {n,r,z{\kern 1pt} '} \right)} \right],\quad {\text{если}}\quad 0 < z{\kern 1pt} ' \leqslant L(n) \wedge \left| r \right| < a(n), \hfill \\ {{\mu }_{0}}{{H}_{z}}\left( {n,r,z{\kern 1pt} '} \right)\quad {\text{везде}}{\text{.}} \hfill \\ \end{gathered} \right.$

Расчетная схема пондеромоторных сил для системы 3-х цилиндров (катушек) $n = 3$ приведена на рис. 4.

Рис. 4.

$j(n)$ – плотность поверхностного тока n-го цилиндра (катушки), ${{M}_{z}}(n)$ – намагниченность $n$-го слоя цилиндра, $z0$ – сдвиг n-го цилиндра относительно начала координат.

В расчетных формулах введены следующие обозначения: $M$ – число слоев катушки (цилиндров); $n$ – порядковый номер слоя ($n = 1,...,M$); $2a1$ – диаметр 1-го слоя; $2an$ – диаметр $n$-го слоя; $2aM$ – диаметр внешнего слоя; $L(n)$ – длина $n$-го цилиндра; $w(n)$ – число витков $n$-го слоя катушки.

В статье для демонстрации модели принято: концентрические цилиндры имеют равные длины $L(n)$, число слоев цилиндров $M = 3$. Для задания расстояния между слоями по $r$ выбрана степенная функция

$Funck(aM,a1,n,k) = \left[ {{{{\left( {{{n - 1} \mathord{\left/ {\vphantom {{n - 1} {M - 1}}} \right. \kern-0em} {M - 1}}} \right)}}^{k}}} \right] \cdot \left( {aM - a1} \right),$

где $k$ – показатель степени; $k = 1$ соответствует равным расстояниям между слоями. Радиус n-го слоя определяется как

$a(n) = \left| \begin{gathered} a1,\;{\text{если}}\quad n = 1 \vee M = 1, \hfill \\ {\text{не}}\;{\text{число}},\;{\text{если}}\quad n > M, \hfill \\ a1 + Funck(aM,a1,n,k)\quad {\text{везде}}{\text{. }} \hfill \\ \end{gathered} \right.$

Ниже приведены результаты расчетов для следующих параметров системы:

$a(n) = \left| \begin{gathered} 10\;{\text{см,}}\quad n = 1, \hfill \\ 15\;{\text{см,}}\quad n = 2, \hfill \\ 20\;{\text{см,}}\quad n = 3; \hfill \\ \end{gathered} \right.\quad L(n) = \left| \begin{gathered} 20\;{\text{см}},\quad n = 1, \hfill \\ 20\;{\text{см,}}\quad n = 2, \hfill \\ 20\;{\text{см}},\quad n = 3; \hfill \\ \end{gathered} \right.\quad w(n) = \left| \begin{gathered} 100,\quad n = 1, \hfill \\ 100,\quad n = 2, \hfill \\ 100,\quad n = 3; \hfill \\ \end{gathered} \right.$

${{M}_{z}}(n) = \left| \begin{gathered} 2.5 \times {{10}^{3}}\;{\text{A/м}},\quad n = 1, \hfill \\ 2.5 \times {{10}^{3}}\;{\text{A/м}},\quad n = 2, \hfill \\ 2.5 \times {{10}^{3}}\;{\text{A/м}},\quad n = 3; \hfill \\ \end{gathered} \right.\quad I(n) = \left| \begin{gathered} 5\;{\text{A}},\quad n = 1, \hfill \\ 5\;{\text{A}},\quad n = 2, \hfill \\ 5\;{\text{A}},\quad n = 3; \hfill \\ \end{gathered} \right.$

$Funck(aM,a1,n,k) = \left| \begin{gathered} 0\;{\text{см}},\quad n = 1, \hfill \\ 5\;{\text{см}},\quad n = 2, \hfill \\ 10\;{\text{см}},\quad n = 3. \hfill \\ \end{gathered} \right.$

Энергия п-го цилиндра в поле i-го определяется формулой

(12)

${{E}_{{cyl}}}(n,i,r,z) = 2\pi \int\limits_{ - L(n){\text{/}}2}^{L(n)/2} {\int\limits_0^{an(n)} {\frac{{Mz(n){{B}_{z}}(i)}}{2}} } rdrdz,\quad i = 1{\kern 1pt} ...\,n.$

При n = i получаем внутреннюю энергию n-го цилиндра. Взаимные энергии цилиндров равны. Равенство взаимных энергий не означает равенство взаимных поверхностных напряжений, что объясняется различной площадью поверхности цилиндров вследствие различия их диаметров.

Радиальная $\langle \sigma n{{i}_{r}}\rangle $ и аксиальная $\langle \sigma n{{i}_{z}}\rangle $ плотности сил по цилиндрической и торцевой поверхностям n-го цилиндра в собственном поле ${{B}_{z}}(n)$ (усредненные по поверхностям) напряжения Н/м² равны

(13)

$\langle \sigma n{{i}_{r}}\rangle = \frac{d}{{dan(n)}}{{{{E}_{{cyl}}}(n,i,r,z))} \mathord{\left/ {\vphantom {{{{E}_{{cyl}}}(n,i,r,z))} {L(n)2\pi an(n)}}} \right. \kern-0em} {L(n)2\pi an(n)}},$

(14)

$\langle \sigma n{{i}_{z}}\rangle = \frac{d}{{dL(n)}}{{{{E}_{{cyl}}}(n,i,r,z))} \mathord{\left/ {\vphantom {{{{E}_{{cyl}}}(n,i,r,z))} {\pi an{{{(n)}}^{2}}}}} \right. \kern-0em} {\pi an{{{(n)}}^{2}}}}.$

Далее для демонстрации конкретных методов и результатов расчетов используется упрощенная запись основных соотношений. В уравнениях индекс $n$ заменяется числами 1, 2, 3. Таким образом, в расчетах теперь фигурируют три цилиндра, между которыми определяются энергетические зависимости. Такой метод делает вычисления более прозрачными и удобен для систем, содержащих небольшое число цилиндров (ориентировочно до пяти). В противном случае необходимо полностью использовать приведенный метод программирования.

Расчет напряжений в системе 3-х концентрических цилиндров (z0 = 0). В новом определении (обозначении) первой цифрой 1 обозначается рассчитываемый цилиндр или катушка. Последующие цифры относятся к внешним относительно его магнитным системам. Вместо индекса $n$ используется запись: $Mz(n = 2) \to Mz2$, ${{B}_{z}}(n = 1) \to {{B}_{z}}1$, ${{B}_{z}}(n = 3) \to {{B}_{z}}3$. В новом обозначении, например, энергия 2-го цилиндра в полях 1-го и 3-го записывается в виде

(15)

$E{{213}_{{cyl}}}(L2,a2) = 2\pi \int\limits_{ - L(2){\text{/}}2}^{L(2){\text{/}}2} {\int\limits_0^{a2} {\frac{{{{M}_{z}}2({{B}_{z}}1(Mz1,a1,r,z,L1) + {{B}_{z}}3(Mz3,a3,r,z,L3)}}{2}} } rdrdz.$

Радиальная плотность силы по цилиндрической поверхности 2-го цилиндра в поле 1-го равна

(16)

$\langle \sigma {{21}_{r}}\rangle = \frac{d}{{da2}}{{E{{{21}}_{{cyl}}}(L2,a2)} \mathord{\left/ {\vphantom {{E{{{21}}_{{cyl}}}(L2,a2)} {h2\pi a}}} \right. \kern-0em} {h2\pi a}}2.$

Для плотности силы по поверхности 1-го цилиндра в поле 2-го имеем

(17)

$\langle \sigma {{12}_{r}}\rangle = - \frac{d}{{da1}}{{E{{{12}}_{{cyl}}}(L1,a1)} \mathord{\left/ {\vphantom {{E{{{12}}_{{cyl}}}(L1,a1)} {h2\pi a}}} \right. \kern-0em} {h2\pi a}}1.$

Легко рассчитываются напряжения, действующие на выделенный цилиндр в поле 2-х других. Так, например, суммарные радиальные напряжения 2-го цилиндра в полях 1-го и 3-го определяются как

(18)

$\langle \sigma {{213}_{r}}\rangle = \frac{{dy}}{{da2}}\left[ {\frac{{E21(L1,a1) + E23(L3,a3)}}{{L2\pi a2}}} \right] = \langle \sigma {{21}_{r}}\rangle + \langle \sigma {{23}_{r}}\rangle .$

Аналогично суммируются аксиальные напряжения.

На рис. 5 показаны взаимные радиальные механические напряжения по образующим цилиндров 3-х попарно.

Рис. 5.

Поверхностные радиальные напряжения цилиндров. $\left\langle {\sigma {{1}_{r}}} \right\rangle $, $\left\langle {\sigma {{2}_{r}}} \right\rangle $, $\left\langle {\sigma {{3}_{r}}} \right\rangle $ – напряжения, действующие на цилиндрические поверхности отдельных цилиндров в собственных полях (Н/м²). $\left\langle {\sigma {{1}_{r}}} \right\rangle = 2.275$, $\left\langle {\sigma {{2}_{r}}} \right\rangle = 1.867$, $\left\langle {\sigma {{3}_{r}}} \right\rangle = 1.588$. Взаимные напряжения:$\left\langle {\sigma {{{12}}_{r}}} \right\rangle = 2.259$, $\left\langle {\sigma {{{21}}_{r}}} \right\rangle = 1.43$, $\left\langle {\sigma {{{23}}_{r}}} \right\rangle = 2.078$, $\left\langle {\sigma {{{32}}_{r}}} \right\rangle = 1.767$, $\left\langle {\sigma {{{13}}_{r}}} \right\rangle = 1.801$, $\left\langle {\sigma {{{31}}_{r}}} \right\rangle = 0.818$.

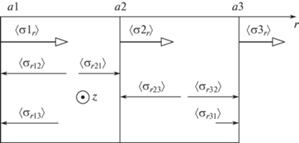
Длины стрелок изображены в масштабе. Результирующие радиальные напряжения, действующие на отдельный цилиндр, получаются (с учетом знака) суммированием напряжений по приведенной схеме рисунка. Так $\left\langle {\sigma {{{132}}_{r}}} \right\rangle $ = $\left\langle {\sigma {{{13}}_{r}}} \right\rangle $ + $\left\langle {\sigma {{{12}}_{r}}} \right\rangle $ = 4.06, что соответствует расчетам по формуле (18).

Аксиальные напряжения рассчитываются по такой же схеме и эти вычисления в статье не приводятся. Попарные продольные (аксиальные) силы H при смещении n-го цилиндра в поле i-го в Z-направлении (рис. 3) вычисляются по формуле ${{F}_{z}}_{{ni}}(z0)$ = = ${{d{{E}_{{ni}}}} \mathord{\left/ {\vphantom {{d{{E}_{{ni}}}} {dz0}}} \right. \kern-0em} {dz0}}$. Для системы цилиндров результирующая сила получается простым суммированием. Например, при смещении 2-го цилиндра с учетом полей 1-го и 2-го цилиндров ${{F}_{z}}213(z0)$ = ${{dE213(z0)} \mathord{\left/ {\vphantom {{dE213(z0)} {dz0}}} \right. \kern-0em} {dz0}}$.

На рис. 6 построены графики аксиальных сил ${{F}_{z}}$, действующих на $n$-й цилиндр ($n = 1,2$) при смещении в Z-направлении, и соответствующих взаимных индуктивностей $M$ эквивалентных катушек (рис. 4).

Рис. 6.

1 – ${{F}_{z}}213$ ($n = 2$); 2 – ${{F}_{z}}123$ ($n = 1$); 3 – $M213$ ($n = 2$); 4 – $M123$ ($n = 1$).

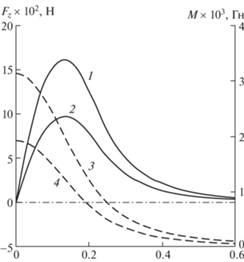
Радиальные силы стремятся увеличить диаметр магнитной системы, а аксиальные приводят к сжатию системы с торцов. Для катушек возникновение таких сил следует из закона Ампера.

В случае однородно намагниченного цилиндра полная энергия увеличивается с ростом его диаметра, т.к. возрастает объем цилиндра и размагничивающее поле. Однако плотность энергии размагничивания равна

${{E}_{p}}(L,a,r,z) = \left( {1{\text{/}}L\pi {{a}^{2}}} \right)2\pi \int\limits_{ - L{\text{/}}2}^{L{\text{/}}2} {\int\limits_0^a {(Mz{{B}_{z}}(L,a,r,z)} } {\text{/}}2)rdrdz,\quad ({\text{Дж/м}}),$

и уменьшается, что и приводит к возникновению сил, увеличивающих диаметр цилиндра.

Индуктивности n = i и взаимные индуктивности катушек вычисляются из энергий и взаимных энергий цилиндров

(19)

${{M}_{{ni}}} = {{2{{E}_{{ni}}}(n,i)} \mathord{\left/ {\vphantom {{2{{E}_{{ni}}}(n,i)} {I(n)I(i)}}} \right. \kern-0em} {I(n)I(i)}}.$

В табл. 1 суммированы основные результаты расчетов параметров магнитной системы с используемой в статье модели.

Таблица 1.

Параметры магнитной системы $n = 3$

Радиус и номер цилиндра $a(n)$, см	Энергия цилиндра ${{E}_{n}}$, Дж	Радиальные напряжения цилиндра $\left\langle {{{\sigma }_{r}}} \right\rangle $, Н/м²	Аксиальные напряжения цилиндра $\left\langle {{{\sigma }_{z}}} \right\rangle $, Н/м²	Взаимные энергии цилиндров ${{E}_{{ni}}}$, Дж	Взаимные радиальные напряжения $\left\langle {\sigma {{n}_{{rni}}}} \right\rangle $, Н/м²	Индуктивность катушек ${{L}_{n}}$, 10³ Гн	Взаимная индуктивность катушек ${{M}_{{ni}}}$, 10⁴ Гн
$a1 = 10$	0.017	–2.276	–3.406	E₁₂ = 0.013	$\left\langle {\sigma {{3}_{{r12}}}} \right\rangle = - 2.585$	${{L}_{1}} = 1.359$	${{M}_{{12}}} = 5.233$
$a2 = 15$	0.033	–1.867	–3.013	E₁₃ = 0.011	$\left\langle {\sigma {{2}_{{r13}}}} \right\rangle = - 3.509$	${{L}_{2}} = 2.643$	${{M}_{{13}}} = 4.811$
$a3 = 20$	0.052	–1.588	–2.714	E₂₃ = 0.026	$\left\langle {\sigma {{1}_{{r23}}}} \right\rangle = - 4.06$	${{L}_{3}} = 4.149$	${{M}_{{23}}} = 11.04$

Выводы. Показана эффективность расчетов магнитных систем, базирующаяся на концепции размагничивающего фактора цилиндра. Многие задачи расчета токовых систем (катушек) традиционно использующие методы электротехники эффективно решаются средствами, представленными в статье. Все расчетные значения взаимной индуктивности системы катушек, поверхностных механических напряжений и продольных пондеромоторных сил соответствуют данным работы [12].

В модели не накладываются какие-либо ограничения на число слоев, геометрические и магнитные параметры цилиндров (катушек) и их взаимное расположение. Магнитные и геометрические параметры систем задаются с учетом поставленной задачи. Метод применим к расчетам систем с параллельными осями. Модель позволяет рассчитывать гибридные магнитные и токовые системы универсальным методом.

Список литературы

Монтгомери Д. Получение сильных магнитных полей с помощью соленоидов. М.: Мир, 1971. 359 с.
Карасик В.Р. Физика и техника сильных магнитных полей. М.: Наука, 1964. 347 с.
Кнопфель Г. Сверхсильные импульсные магнитные поля. М.: Изд. МИР, 1972. 385 с.
Паркинсон Д., Малхолл Б. Получение сильных магнитных полей. М.: Атомиздат. 1971. 200 с.
Алиевский Б.Л., Октябрьский А.М., Орлов В.Л., Постников В.А. Моделирование магнитных полей осесимметричных систем: Учебное пособие / Под ред. Б.Л. Алиевского. М.: Изд-во МАИ, 2007. 320 с.
Андреев А.К. Поле многослойной многовитковой катушки с аналитически заданными законами изменений расстояний между слоями и витками // Проблемы машиностроения и надежности машин. 2019. № 1. С. 34. https://doi.org/10.1134/S0235711919010036
Андреев А.К. Метод расчета пондеромоторных сил и взаимных индуктивностей в коаксиальных осесимметричных магнитных системах // Письма в ЖТФ. 2021. Т. 47. Вып. 11. С. 17. https://doi.org/10.21883/PJTF.2021.11.51001.18729
Парселл Э. Электричество и магнетизм. М.: Наука, 1975. 439 с.
Андреев А.К. Метод расчета взаимной индуктивности системы катушек c использованием модели аксиально намагниченного цилиндра // Письма в ЖТФ, 2020. Т. 46. Вып. 21. С. 48. https://doi.org/10.21883/PJTF.2020.21.50198.18042
Ахиезер А.И., Барьяхтар В.Г., Пелетминский С.В. Спиновые волны. М.: Наука, 1967. 368 с.
Bateman H. Partial differential equations of mathematical physics. New York: Dover Publications, 1944. 556 p.
Смайт В. Электростатика и электродинамика. М.: Изд. Иностранной литературы, 1954. 604 с.
Joseph R.J., Schlӧmann J. Demagnetizing Field in Nonellipsoidal Bodies // Appl. Phys. 1964. V. 36. № 5. P. 1579.
Андреев А.К. Метод расчета поверхностных механических напряжений в осесимметричных магнитных системах // Письма в ЖТФ. 2021. Т. 47. Вып. 9. С. 41. https://doi.org/10.21883/PJTF.2021.09.50907.18626
Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей: Справочная книга. Л.: Энергоатомиздат, 1986. 488 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал