Проблемы машиностроения и надежности машин, 2023, № 1, стр. 16-25

Колебания составной цилиндрической оболочки в жидкости, возбуждаемые дискретной и распределенной нагрузкой

О. И. Косарев^*

Институт машиноведения им. А.А. Благонравова РАН,
Москва, Россия

Поступила в редакцию 06.07.2022
Принята к публикации 20.10.2022

EDN: ASAXNL
DOI: 10.31857/S0235711923010078

Аннотация

Предложен метод расчета вынужденных колебаний составной цилиндрической оболочки, погруженной в жидкость, возбуждаемой совместно дискретными силами и распределенной по длине нагрузкой. Система состоит из цилиндрических оболочек (отсеков), соединенных упругими кольцами.

Ключевые слова: вынужденные колебания, цилиндрическая оболочка, жидкость, дисперсионное уравнение, дискретные силы, распределенная нагрузка

Рассматривается задача о вынужденных колебаниях составной оболочки со свободными краевыми условиями, погруженной в жидкость. Конструкция состоит из соединенных между собой цилиндрических оболочек и упругих колец, возбуждаемых дискретной и распределенной нагрузкой.

Задача о вынужденных колебаниях составных оболочек в жидкости может иметь как самостоятельное значение в области акустического проектирования объектов, так и быть частью более сложных задач. Оболочечные конструкции широко применяются в технике. Вопросам колебаний цилиндрических оболочек посвящена обширная литература [1–11]. В большинстве случаев рассматривались бесконечные оболочки или с краевыми условиями Навье. Например, в работе [1] при решении задачи дифракции на цилиндрической оболочке для определения деформаций использовались уравнения колебаний оболочки. Однако решалась плоская задача, т.е. радиальные перемещения оболочки определялись только в плоскости поперечного сечения. В работе [2] рассматривалась бесконечная цилиндрическая оболочка, которая возбуждалась сосредоточенной силой, выраженной через дельта-функцию Дирака. При этом решение для радиальных перемещений было представлено в виде

$w = \frac{1}{{2\pi }}\sum\limits_{n = 0}^\infty {\int\limits_{ - \infty }^\infty {\tilde {w}} {{e}^{{i{{k}_{z}}z}}}} d{{k}_{z}},$

где k_z – осевое волновое число волны изгибных деформаций оболочки. Такие решения не пригодны для практических расчетов конечных цилиндрических оболочек со свободными краевыми условиями.

Задача вынужденных колебаний составной оболочечной конструкции при совместном действии дискретной и распределенной нагрузки является актуальной и, судя по обзору публикаций [1–11], решение ее в настоящее время отсутствует.

Настоящая статья представляет собой развитие и обобщение метода расчета [3] для случая совместного действия дискретной и распределенной нагрузки. В работе [3] рассмотрены колебания составной оболочки, возбуждаемые дискретными силами, приложенными к кольцам. В отличие от [3] в настоящей статье изучаются вынужденные колебания составной цилиндрической оболочки в случае возбуждения колебаний совместно дискретными силами и распределенной нагрузкой (давлением).

Динамическая модель составной оболочки, состоящей из секций (отсеков), каждая из которых представляет собой упругую цилиндрическую оболочку с упругими кольцами на концах (торцах), показана на рис. 1 [3].

Рис. 1.

Динамическая модель составной оболочки.

Здесь, так же, как в [3], при расчете колебаний составная оболочка условно разбивается на подсистемы, включающие оболочки (отсеки) и кольца. Для каждой оболочки (отсека) составляются дисперсионные уравнения и определяются их корни. Функция распределения перемещений оболочек (отсеков) по их длине записывается через перемещения торцевых сечений.

Целью является разработка метода расчета вынужденных колебаний составной цилиндрической оболочки в жидкости, возбуждаемых совместно дискретной и распределенной нагрузками. Дискретная нагрузка – это силы, сосредоточенные по длине оболочки (по окружности они распределены по гармоническому закону cos nφ и sin nφ), а распределенная нагрузка – это давление на оболочку окружающей среды.

Новизна разработки заключается в учете совместного действия двух типов нагрузок, из которых метод расчета вынужденных колебаний, возбуждаемых динамическим давлением, конечной составной цилиндрической оболочки со свободными краевыми условиями, погруженной в жидкость, является новым.

Полезность разработки обусловлена следующим обстоятельством. В ряде случаев вибрации передаются на корпус, моделируемый цилиндрической оболочкой, по металлической конструкции и по окружающей среде (в частности жидкости). Дополнительный учет второго пути расширяет возможности метода расчета, делает его более универсальным и повышает его точность.

Ниже приведены формулы, относящиеся к оболочке-отсеку, или из нескольких соединенных оболочек-отсеков и колец.

Уравнения движения цилиндрической оболочки в перемещениях, основаны на моментной теории упругих оболочек Кирхгофа–Лява, имеют вид [4, 5]

(1)

$\begin{gathered} \frac{{\partial {{T}_{1}}}}{{\partial z}} + \frac{{\partial S}}{{\partial \varphi }} - {{\rho }_{*}}ha\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} + a{{q}_{1}} = 0, \\ \frac{{\partial {{T}_{2}}}}{{\partial \varphi }} + \frac{{\partial S}}{{\partial z}} + \frac{1}{a}\left( {\frac{{\partial {{M}_{2}}}}{{\partial \varphi }} + 2\frac{{\partial H}}{{\partial z}}} \right) - {\text{ }}{{\rho }_{*}}ha\frac{{{{\partial }^{2}}{v}}}{{\partial {{t}^{2}}}} + a{{q}_{2}} = 0, \\ \frac{1}{a}\left( {\frac{{{{\partial }^{2}}{{M}_{1}}}}{{\partial {{z}^{2}}}} + 2\frac{{{{\partial }^{2}}H}}{{\partial z\partial \varphi }} + \frac{{{{\partial }^{2}}{{M}_{2}}}}{{\partial {{\varphi }^{2}}}}} \right) - {{T}_{2}} - {{\rho }_{*}}ha\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} - a{{q}_{3}} = 0, \\ \end{gathered} $

где u, ${v}$, w – продольные, окружные и радиальные перемещения оболочки; T₁, T₂, S, H, M₁, M₂ – упругие силовые факторы; a, h – радиус и толщина оболочки; z – осевая безразмерная координата в долях радиуса a; φ – окружная координата; t – время; ${{\rho }_{*}}$ – плотность материала оболочки; 0 ≤ z ≤ $\ell $, $\ell $ = L/a, L – длина оболочки; q₁, q₂, q₃ – поверхностные распределенные нагрузки.

Считаем, что внешняя распределенная нагрузка (давление) действует по нормали к поверхности оболочки (радиально), поэтому принимаем q₁ = q₂ = 0, q₃ = pe^iθz.

Полные решения уравнений (1) для каждой гармоники n записываются в виде

(2)

$\begin{gathered} u = U{{e}^{{i\omega t}}}\cos n\varphi + u{\kern 1pt} *,\quad {v} = V{{e}^{{i\omega t}}}\sin n\varphi + {v}{\kern 1pt} *,\quad w = W{{e}^{{i\omega t}}}\cos n\varphi + w{\kern 1pt} *{\kern 1pt} , \\ U = {\text{ }}\sum\limits_{j = 1}^8 {{{C}_{{jn}}}} \frac{{\Delta _{{jn}}^{{\left( 2 \right)}}}}{{\Delta _{{jn}}^{{\left( 1 \right)}}}}{\text{ }}{{e}^{{\lambda z}}},\quad V = {\text{ }}\sum\limits_{j = 1}^8 {{{C}_{{jn}}}} \frac{{\Delta _{{jn}}^{{\left( 3 \right)}}}}{{\Delta _{{jn}}^{{\left( 1 \right)}}}}{\text{ }}{{e}^{{\lambda z}}},\quad W = {\text{ }}\sum\limits_{j = 1}^8 {{{C}_{{jn}}}} {{e}^{{\lambda z}}}, \\ \end{gathered} $

где n – окружные гармоники, С_jn – искомые коэффициенты, $\Delta _{{j,n}}^{{(1)}}$, $\Delta _{{j,n}}^{{(2)}}$, $\Delta _{{j,n}}^{{(3)}}$, – миноры матрицы уравнения движения оболочки; ω = 2πf – угловая частота колебаний; f – частота колебаний; λ – корни дисперсионного уравнения; t – время; φ – окружная координата, i – мнимое число; u*, ${v}{\kern 1pt} *$, w* – частные решения уравнения (1), перемещения вынужденных колебаний, возбуждаемых распределенной нагрузки q₃.

Для определения показателей экспонент λ, являющихся корнями дисперсионного уравнения, подставим в уравнение (1) решения вида

$u = U \cdot {{e}^{{\lambda z}}}\cos n\varphi ;\quad {v} = V \cdot {{e}^{{\lambda z}}}\sin \varphi ;\quad w = W \cdot {{e}^{{\lambda z}}}\cos n\varphi ,$

и получим уравнение свободных колебаний оболочки в матричной форме

(3)

$\left[ {\begin{array}{*{20}{c}} {{{L}_{{11}}} + \omega _{*}^{2}}&{{{L}_{{12}}}}&{{{L}_{{13}}}} \\ { - {{L}_{{12}}}}&{{{L}_{{22}}} + \omega _{*}^{2}}&{{{L}_{{23}}}} \\ { - {{L}_{{13}}}}&{{{L}_{{23}}}}&{{{L}_{{33}}} + \omega _{*}^{2}} \end{array}} \right] \cdot \left\{ {\begin{array}{*{20}{c}} U \\ V \\ W \end{array}} \right\} = \frac{a}{g}\left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {{{q}_{3}}} \end{array}} \right\},$

где в случае свободных колебаний q₃ = p_s – реакция жидкости на колебания оболочки.

Элементы левой матрицы L_i, _j в уравнении (3)

${{L}_{{11}}} = {{\lambda }^{2}} - \frac{{1 - \mu }}{2}{{n}^{2}},\quad {{L}_{{12}}} = \frac{{1 + \mu }}{2}\lambda n = - {{L}_{{21}}},\quad {{L}_{{13}}} = \lambda \mu ,$

${{L}_{{22}}} = \frac{{1 - \mu }}{2}\left( {1 + 4{{\delta }^{2}}} \right){{\lambda }^{2}} - {{n}^{2}}\left( {1 + {{b}_{2}} + 2\frac{{{{z}_{2}}{{b}_{2}}}}{r} + {{\delta }^{2}} + \frac{{{{a}_{2}}}}{{{{r}^{2}}}}} \right),$

(4)

${{L}_{{23}}} = {{L}_{{32}}} = - n\left[ {1 + {{b}_{2}} + \frac{{{{z}_{2}}{{b}_{2}}}}{r} - \left( {2 - \mu } \right){{\delta }^{2}}{{\lambda }^{2}} + {{n}^{2}}\left( {{{\delta }^{2}} + \frac{{{{z}_{2}}{{b}_{2}}}}{r} + \frac{{{{a}_{2}}}}{{{{r}^{2}}}}} \right)} \right],$

${{L}_{{31}}} = - {{L}_{{13}}},\quad {{L}_{{33}}} = - 1 - {{b}_{2}} - {{n}^{4}}\frac{{{{a}_{2}}}}{{{{r}^{2}}}} - {{\delta }^{2}}{{\left( {{{\lambda }^{2}} - {{n}^{2}}} \right)}^{2}} - 2\frac{{{{z}_{2}}{{b}_{2}}}}{r}.$

$\omega _{*}^{2} = \frac{{{{\omega }^{2}}{{r}^{2}}{{\rho }_{*}}\left( {1 - {{\mu }^{2}}} \right)}}{E},\quad g = \frac{{Eh}}{{\left( {1 - {{\mu }^{2}}} \right)r}},$

где μ – коэффициент Пуассона; r = a – радиус оболочки; E – комплексный модуль упругости; ${{\rho }_{*}}$ – плотность материала оболочки; a₂, z₂, b₂ – параметры шпангоутов в случае их конструктивной ортотропии (равномерного распределения параметров по длине оболочки) для низких частот колебаний [6]. Для высоких частот колебаний шпангоуты могут быть представлены в виде колец.

Миноры и определитель матрицы L_i, _j левой части уравнения (3)

$\Delta _{{}}^{{(1)}} = {{L}_{{11}}}{{L}_{{22}}} + L_{{12}}^{2} + \omega _{*}^{2}\left( {{{L}_{{11}}} + {{L}_{{22}}}} \right) + \omega _{*}^{4},\quad \Delta _{{}}^{{(2)}} = {{L}_{{12}}}{{L}_{{23}}} - {{L}_{{13}}}{{L}_{{22}}} - \omega _{*}^{2}{{L}_{{13}}},$

(5)

$\begin{gathered} \Delta _{{}}^{{(3)}} = - {{L}_{{13}}}{{L}_{{12}}} - ({{L}_{{11}}} + \omega _{*}^{2}){{L}_{{23}}}, \\ {{\Delta }_{0}} = ({{L}_{{11}}} + \omega _{*}^{2})({{L}_{{22}}} + \omega _{*}^{2})({{L}_{{33}}} + \omega _{*}^{2}) - {{L}_{{12}}}{{L}_{{23}}}{{L}_{{13}}} - {{L}_{{13}}}{{L}_{{12}}}{{L}_{{23}}} + \\ \end{gathered} $

$ + \;{{L}_{{13}}}({{L}_{{22}}} + \omega _{*}^{2}){{L}_{{13}}} - ({{L}_{{11}}} + \omega _{*}^{2})L_{{23}}^{2} + L_{{12}}^{2}{{L}_{{33}}}.$

Корни дисперсионного уравнения с учетом замены λ = iα определяются из решения дисперсионного уравнения [3]

(6)

$\frac{{{{\Delta }_{0}}(\alpha )}}{{{{\Delta }^{{(1)}}}(\alpha )}} - \frac{{{{\rho }_{0}}{{\omega }^{2}}aH_{n}^{{(2)}}(ka)}}{{gkH_{n}^{{(2)}}{\kern 1pt} '{\kern 1pt} (ka)}} = 0,$

где Δ⁽¹⁾(α) = Δ⁽¹⁾ и Δ₀(α) = Δ₀ с элементами (5), в которых λ = iα; ρ₀ – плотность жидкости, k = ω/c – волновое число; с – скорость звука в жидкости; $H_{n}^{{(2)}}$(ka) – функция Ганкеля второго рода.

Из решения дисперсионного уравнения (6) определяются восемь корней α_j в решении (2), для каждой гармоники n на каждой частоте колебаний f.

Вынужденные колебания, возбуждаемые дискретными силами Р, приложенными к кольцам, передаются на оболочки через их связи с кольцами. Кольца могут быть как реальными, так и виртуальными (безынерционными), расположенными при необходимости в любом месте на оболочке, где нужно приложить силы. Непосредственно на поверхность оболочки действует только распределенная нагрузка (давление) q₃ = pe^iθz, которая возбуждает вынужденные колебания оболочки.

Определим частые решения вынужденных колебаний оболочки. Частные решения u* = U*e^iωt cos nφ, ${v}{\kern 1pt} *$ = V*e^iωt sin φ, w* = W*e^iωt cos nφ уравнения вынужденных колебаний оболочки от действия распределенной нагрузки q₃ = pe^iθz определим из решения уравнения (3), обозначив матрицу в левой части уравнения (3) L_i, j, где λ = iθ

$\left\{ \begin{gathered} U{\kern 1pt} * \hfill \\ V{\kern 1pt} * \hfill \\ W{\kern 1pt} * \hfill \\ \end{gathered} \right\} = \frac{a}{g}{{\left[ {{{L}_{{i,j}}}} \right]}^{{ - 1}}}\left\{ \begin{gathered} 0 \hfill \\ 0 \hfill \\ {{q}_{3}} \hfill \\ \end{gathered} \right\}.$

Радиальные перемещения будут

$W{\kern 1pt} * = \frac{{{{\Delta }^{{(1)}}}(\theta )}}{{{{\Delta }_{0}}(\theta )}}\frac{a}{g}{{q}_{3}},$

где Δ⁽¹⁾(θ) = Δ⁽¹⁾ и Δ₀ (θ) = Δ₀ при λ = iθ.

Определим зависимости, связывающие текущие перемещения поверхности оболочки с перемещениями ее концов. Предварительно к трем перемещениям u, ${v}$, w добавим четвертое перемещение, производную w' = ∂w/∂z, угол поворота. Перемещение w' добавлено для возможности состыковки оболочек и колец по четырем силовым факторам, для проведения преобразований перемещений и составления сводного уравнения колебаний составной оболочки в матричной форме.

Перемещения свободных колебаний представим вектором четвертого порядка

$\zeta (z) = {{\left\{ {u,{v},w,w{\kern 1pt} '{\kern 1pt} } \right\}}^{T}}.$

Частные решения, перемещения вынужденных колебаний, с учетом

$U{\kern 1pt} * = \frac{{{{\Delta }^{2}}(\theta )}}{{{{\Delta }^{1}}(\theta )}}W{\kern 1pt} *{\kern 1pt} ,\quad V{\kern 1pt} * = \frac{{{{\Delta }^{3}}(\theta )}}{{{{\Delta }^{1}}(\theta )}}W{\kern 1pt} *{\kern 1pt} ,$

также представим вектором четвертого порядка

$\zeta {\kern 1pt} * = {{\left\{ {u{\kern 1pt} *{\kern 1pt} ,{v}{\kern 1pt} *{\kern 1pt} ,w{\kern 1pt} *{\kern 1pt} ,w{\kern 1pt} *{\kern 1pt} '{\kern 1pt} } \right\}}^{T}} = w{\kern 1pt} *{{\left\{ {\frac{{{{\Delta }^{2}}(\theta )}}{{{{\Delta }^{1}}(\theta )}},\frac{{{{\Delta }^{3}}(\theta )}}{{{{\Delta }^{1}}(\theta )}},1,i\theta } \right\}}^{T}}.$

Полные решения (2) представим в матричной форме

$\zeta (z) = {\text{ }}\left\{ {\begin{array}{*{20}{c}} {\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{1}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{1}}} \right)}}}&{\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{2}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{2}}} \right)}}}& \cdots &{\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{8}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{8}}} \right)}}} \\ {\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{1}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{1}}} \right)}}}&{\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{2}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{2}}} \right)}}}& \cdots &{\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{8}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{8}}} \right)}}} \\ 1&1& \cdots &1 \\ {i{{\alpha }_{1}}}&{i{{\alpha }_{2}}}& \cdots &{i{{\alpha }_{8}}} \end{array}} \right\}{\text{ }}\left\{ {\begin{array}{*{20}{c}} {{{e}^{{i{{\alpha }_{1}}z}}}}&0&0& \cdots &0 \\ 0&{{{e}^{{i{{\alpha }_{2}}z}}}}&0& \cdots &0 \\ 0&0&{{{e}^{{i{{\alpha }_{3}}z}}}}& \cdots &0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &{{{e}^{{i{{\alpha }_{8}}z}}}} \end{array}} \right\}{\text{ }}\left\{ {\begin{array}{*{20}{c}} {{{{\text{C}}}_{1}}} \\ {{{{\text{C}}}_{2}}} \\ {{{{\text{C}}}_{3}}} \\ \vdots \\ {{{{\text{C}}}_{8}}} \end{array}} \right\} + \zeta {\kern 1pt} *{\kern 1pt} .$

Обозначим

$G(\alpha ) = \left\{ {\begin{array}{*{20}{c}} {\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{1}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{1}}} \right)}}}&{\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{2}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{2}}} \right)}}}& \cdots &{\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{8}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{8}}} \right)}}} \\ {\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{1}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{1}}} \right)}}}&{\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{2}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{2}}} \right)}}}& \cdots &{\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{8}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{8}}} \right)}}} \\ 1&1& \cdots &1 \\ {i{{\alpha }_{1}}}&{i{{\alpha }_{2}}}& \cdots &{i{{\alpha }_{8}}} \end{array}} \right\}{\text{,}}\quad \beta (z) = \left\{ {\begin{array}{*{20}{c}} {{{e}^{{i{{\alpha }_{1}}z}}}}&0&0& \cdots &0 \\ 0&{{{e}^{{i{{\alpha }_{2}}z}}}}&0& \cdots &0 \\ 0&0&{{{e}^{{i{{\alpha }_{3}}z}}}}& \cdots &0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &{{{e}^{{i{{\alpha }_{8}}z}}}} \end{array}} \right\}{\text{.}}$

Преобразуем выражение ζ(z), чтобы текущие перемещения выразить через перемещения концов оболочки. Обозначим

${{С}_{j}} = {{\left. {\left\{ {{{С}_{1}}} \right.,{{C}_{2}},{{C}_{3}},...,{{C}_{8}}} \right\}}^{T}},\quad G(z) = G(\alpha )\beta (z).$

В краткой записи текущее перемещение

$\zeta (y) = G(z){{C}_{j}} + \zeta {\kern 1pt} *{\kern 1pt} (y).$

Перемещения на концах оболочки при z = 0 и z = $\ell $

$\zeta (0) = G(0){{C}_{j}} + \zeta {\kern 1pt} *{\kern 1pt} (0),\quad \zeta (l) = G(l){{C}_{j}} + \zeta {\kern 1pt} *{\kern 1pt} (l).$

В матричной форме

$\left\{ \begin{gathered} \zeta (0) - \zeta {\kern 1pt} *{\kern 1pt} (0) \hfill \\ \zeta (l) - \zeta {\kern 1pt} *{\kern 1pt} (l) \hfill \\ \end{gathered} \right\} = \left[ \begin{gathered} G(0) \hfill \\ G(l) \hfill \\ \end{gathered} \right]{{C}_{j}}.$

Отсюда путем обращения матрицы, найдем

(7)

$\begin{gathered} {{С}_{j}} = {{\left[ \begin{gathered} G(0) \hfill \\ G(l) \hfill \\ \end{gathered} \right]}^{{ - 1}}}\left\{ \begin{gathered} \zeta (0) - \zeta {\kern 1pt} *{\kern 1pt} (0) \hfill \\ \zeta (\ell ) - \zeta {\kern 1pt} *{\kern 1pt} (\ell ) \hfill \\ \end{gathered} \right\} = \left[ {{{B}_{1}},{{B}_{2}}} \right]\left\{ \begin{gathered} \zeta (0) - \zeta {\kern 1pt} *{\kern 1pt} (0) \hfill \\ \zeta (l) - \zeta {\kern 1pt} *{\kern 1pt} (l) \hfill \\ \end{gathered} \right\} = \\ = {{B}_{1}}(\zeta (0) - {{\zeta }_{{v}}}(0)) + {{B}_{2}}(\zeta (l) - {{\zeta }_{{v}}}(l)). \\ \end{gathered} $

В результате получим текущие перемещения в оболочке, выраженные через перемещения ее концов оболочки

(8)

$\zeta (z) = G(z)\left[ {{{B}_{1}}({{\zeta }_{0}} - \zeta _{0}^{*}) + {{B}_{2}}({{\zeta }_{\ell }} - \zeta _{\ell }^{*})} \right] + \zeta {\kern 1pt} *{\kern 1pt} (z),$

где ζ₀ = ζ(0), ${{\zeta }_{\ell }}$ = ζ($\ell $) – перемещения свободных колебаний; $\zeta _{0}^{*} = {\text{ }}\zeta {\kern 1pt} *{\kern 1pt} \left( 0 \right)$, $\zeta _{\ell }^{*} = {\text{ }}\zeta {\kern 1pt} *{\kern 1pt} \left( \ell \right)$ – перемещения вынужденных колебаний от давления q₃ в начале и в конце z = $\ell $ оболочки. Матрица $G\left( z \right)$ размером 4 × 8 состоит из восьми столбцов G_j по числу корней α_j

$G\left( z \right) = \left\{ {{{G}_{j}}} \right\},\quad {\text{где}}\quad j = 1,2, \ldots 8;\quad {{G}_{j}} = {{e}^{{i{{\alpha }_{j}}z}}}{{\left\{ {\frac{{{{\Delta }^{{(2)}}}}}{{{{\Delta }^{{(1)}}}}},\frac{{{{\Delta }^{{(3)}}}}}{{{{\Delta }^{1}}}},1,i{{\alpha }_{j}}} \right\}}^{T}},$

где ${{\Delta }^{{(1)}}} = {{\Delta }^{{(1)}}}\left( {{{\alpha }_{j}}} \right)$, ${{\Delta }^{{(2)}}} = {{\Delta }^{{(2)}}}\left( {{{\alpha }_{j}}} \right)$, ${{\Delta }^{{(3)}}} = {{\Delta }^{{(3)}}}\left( {{{\alpha }_{j}}} \right)$.

Матрицы ${{B}_{1}}$, ${{B}_{2}}$ размером 8 × 4 являются блоками квадратной матрицы $B = \left\{ {{{B}_{1}},{{B}_{2}}} \right\}$ размером 8 × 8, (7), а сама матрица $B = {{\left\| {\begin{array}{*{20}{c}} {{{G}_{z}}(0)} \\ {{{G}_{z}}(\ell )} \end{array}} \right\|}^{{ - 1}}}.$

Определим связь внутренних сил и перемещений в оболочке. Согласно моментной теории цилиндрических оболочек, связь внутренних сил и деформаций на срединной поверхности оболочек можно выразить в виде [4, 5]

$T_{1}^{{}} = \frac{{Eh}}{{1 - {{\mu }^{2}}}}\left[ {\frac{1}{r}\frac{{\partial u}}{{\partial z}} + \mu \frac{1}{r}\left( {\frac{{\partial {v}}}{{\partial \varphi }} + w} \right)} \right],$

(9)

$\begin{gathered} S_{1}^{*} = \frac{{Eh}}{{2\left( {1 + \mu } \right)}}\frac{1}{r}\left( {\frac{{\partial u}}{{\partial \varphi }} + \frac{{\partial {v}}}{{\partial z}}} \right) + 2D\left( {1 - \mu } \right)\frac{1}{{{{r}^{2}}}}\left( {\frac{{\partial {v}}}{{\partial z}} - \frac{{{{\partial }^{2}}w}}{{\partial z{\text{ }}\partial \varphi }}} \right), \\ Q_{1}^{*} = \frac{D}{r}\left[ { - \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{3}}w}}{{\partial {{z}^{3}}}} + \frac{M}{{{{r}^{2}}}}\left( {\frac{{{{\partial }^{2}}{v}}}{{\partial z\partial \varphi }} - \frac{{{{\partial }^{3}}w}}{{\partial {{\varphi }^{2}}\partial z}}} \right) + \frac{{2\left( {1 - \mu } \right)}}{{{{r}^{2}}}}\left( {\frac{{{{\partial }^{2}}{v}}}{{\partial z\partial \varphi }} - \frac{{{{\partial }^{3}}w}}{{\partial \varphi {\text{ }}\partial {{z}^{2}}}}} \right)} \right], \\ \end{gathered} $

$M_{1}^{{}} = \frac{D}{{{{r}^{2}}}}\left[ { - \frac{{{{\partial }^{2}}w}}{{\partial {{z}^{2}}}} + \mu \left( {\frac{{\partial {v}}}{{\partial \varphi }} - \frac{{{{\partial }^{2}}w}}{{\partial {{\varphi }^{2}}}}} \right)} \right],$

где D – цилиндрическая жесткость; r = a.

После выполнения дифференцирования в (9)

${{T}_{1}} = g{{e}^{{i\alpha z}}}\left( {i\alpha u + \mu n{v} + \mu w} \right)\cos n\varphi ,$

(10)

$\begin{gathered} S_{1}^{*} = g{{e}^{{i\alpha z}}}\frac{{1 - \mu }}{2}\left\{ { - nu + i\alpha \left( {1 + 4{{\delta }^{2}}} \right){v} + 4i\alpha n{{\delta }^{2}}w} \right\}\sin n\varphi , \\ Q_{1}^{*} = g{{e}^{{i\alpha z}}}i\alpha {{\delta }^{2}}\left\{ {\left( {2 - \mu } \right)n{v} + \left[ {\left( {2 - \mu } \right){{n}^{2}} + {{\alpha }^{2}}} \right]w} \right\}\cos n\varphi , \\ \end{gathered} $

${M \mathord{\left/ {\vphantom {M r}} \right. \kern-0em} r} = g{{e}^{{i\alpha z}}}{{\delta }^{2}}\left[ {\mu n{v} + \left( {\alpha _{{}}^{2} + \mu {{n}^{{\text{2}}}}} \right)w} \right]\cos n\varphi .$

После подстановки перемещений в (10) получим вектор внутренних сил в сечении оболочки

(11)

$\begin{gathered} \eta \left( z \right) = {{\{ {{T}_{1}},S_{1}^{*},Q_{1}^{*},{M \mathord{\left/ {\vphantom {M r}} \right. \kern-0em} r}\} }^{T}}, \\ \eta (z) = G{\kern 1pt} *{\kern 1pt} (z)[{{B}_{1}}({{\zeta }_{0}} - \zeta _{0}^{*}) + {{B}_{2}}({{\zeta }_{\ell }} - \zeta _{\ell }^{*})] + \Phi W{\kern 1pt} *{\kern 1pt} {{e}^{{i\theta z}}}, \\ \end{gathered} $

где $G{\kern 1pt} *{\kern 1pt} \left( z \right)$ – матрица размером 4 × 8, состоящая из восьми столбцов $G_{j}^{*}$ (по числу корней α_j) $G{\kern 1pt} *{\kern 1pt} \left( z \right) = \{ G_{j}^{*}\} $, j = 1, 2, …, 8.

(12)

$G\left( z \right) = g{{e}^{{i\alpha z}}}\left\| {{\text{ }}\begin{array}{*{20}{c}} {i\alpha \frac{{{{\Delta }^{{(2)}}}}}{{{{\Delta }^{{(1)}}}}} + \mu n\frac{{{{\Delta }^{{(3)}}}}}{{{{\Delta }^{{(1)}}}}} + \mu } \\ {\frac{{{\text{1}} - \mu }}{2}\left( { - n\frac{{{{\Delta }^{{(2)}}}}}{{{{\Delta }^{{(1)}}}}} + i\alpha \frac{{{{\Delta }^{{(3)}}}}}{{{{\Delta }^{{(1)}}}}}\left( {{\text{1}} + 4{{\delta }^{{\text{2}}}}} \right) + 4in\alpha {{\delta }^{2}}} \right)} \\ {i\alpha {{\delta }^{2}}\left( {n\left( {{\text{2}} - \mu } \right)\frac{{{{\Delta }^{{(3)}}}}}{{{{\Delta }^{{(1)}}}}} + \left( {{\text{2}} - \mu } \right){{n}^{{\text{2}}}} + {{\alpha }^{2}}} \right)} \\ {n\mu \frac{{\Delta {}^{{(3)}}}}{{{{\Delta }^{{(1)}}}}}{{\delta }^{{\text{2}}}} + \left( {\mu {{n}^{{\text{2}}}} + {{\alpha }^{2}}} \right){{\delta }^{{\text{2}}}}} \end{array}{\text{ }}} \right\|,$

где Δ⁽¹⁾, Δ⁽²⁾, Δ⁽³⁾ – миноры (5) при λ = iα.

Вектор Φ – определяет реакции в сечениях оболочки в направлениях перемещений ζ(z) при действии внешнего давления

(13)

$\Phi = g{{e}^{{i\theta z}}}\left\| {{\text{ }}\begin{array}{*{20}{c}} {i\theta \frac{{{{\Delta }^{{(2)}}}(\theta )}}{{{{\Delta }^{{(1)}}}(\theta )}} + \mu n\frac{{{{\Delta }^{3}}(\theta )}}{{{{\Delta }^{{(1)}}}(\theta )}} + \mu } \\ {\frac{{1 - \mu }}{2}\left[ { - n\frac{{{{\Delta }^{{(2)}}}(\theta )}}{{{{\Delta }^{{(1)}}}(\theta )}} + i\theta (1 + 4\delta _{{}}^{2})\frac{{{{\Delta }^{{(3)}}}(\theta )}}{{{{\Delta }^{{(1)}}}(\theta )}} + 4i\theta n{{\delta }^{2}}} \right]} \\ {i\theta {{\delta }^{2}}\left\{ {n(2 - \mu )\frac{{{{\Delta }^{{(3)}}}(\theta )}}{{{{\Delta }^{{(1)}}}(\theta )}} + \left[ {(2 - \mu {\text{ }}){{n}^{2}} + {{\theta }^{2}}} \right]} \right\}} \\ {{{\delta }^{2}}\left[ {\mu n\frac{{{{\Delta }^{{(3)}}}(\theta )}}{{{{\Delta }^{{(1)}}}(\theta )}}\theta + ({{\theta }^{2}} + \mu {{n}^{2}})} \right]} \end{array}{\text{ }}} \right\|,$

где Δ⁽¹⁾, Δ⁽²⁾, Δ⁽³⁾ – миноры (5) при λ = iθ.

Колебания кольца. Матричное уравнение колебаний кольца для окружных гармоник n ≥ 1

(14)

$\left[ {\begin{array}{*{20}{c}} {{{m}_{{11}}}}&0&0&{{{m}_{{14}}}} \\ 0&{{{m}_{{22}}}}&0&0 \\ 0&0&{{{m}_{{33}}}}&0 \\ {{{m}_{{41}}}}&0&0&{{{m}_{{44}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} u \\ {v} \\ w \\ {\vartheta R} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{q}_{u}}} \\ {{{q}_{{v}}}} \\ {{{q}_{w}}} \\ {{M \mathord{\left/ {\vphantom {M R}} \right. \kern-0em} R}} \end{array}} \right\},$

где u, ${v}$, w, ϑ – перемещения центра масс кольца, соответственно продольное, окружное, радиальное и угол поворота из плоскости. В правой части уравнения (14) записан вектор сосредоточенных нагрузок. Обозначим M_k левую матрицу (14). Элементы матрицы M_k

${{m}_{{11}}} = n_{{}}^{4}G_{3}^{{}} + n_{{}}^{2}G_{t}^{{}} - {{\rho }_{*}}{\text{F}}\omega _{{}}^{{\text{2}}},\quad {{m}_{{14}}} = n_{{}}^{2}\left( {{{G}_{3}} + {{G}_{t}}} \right),\quad {{m}_{{14}}} = {{m}_{{41}}},$

${{m}_{{22}}} = G_{1}^{{}}n_{{}}^{2}{{\left( {{{n}^{2}} - 1} \right)}^{2}} - \left( {{{n}^{2}} + 1} \right){{\rho }_{*}}{\text{F}}{{\omega }^{2}},\quad {{m}_{{33}}} = {{G}_{1}}{{\left( {{{n}^{2}} - 1} \right)}^{2}} - \frac{{\left( {{{n}^{2}} + 1} \right)}}{{{{n}^{2}}}}{{\rho }_{*}}F{{\omega }^{2}},$

${{m}_{{44}}} = G_{3}^{{}} + n_{{}}^{2}G_{t}^{{}},\quad {{G}_{k}} = \frac{{EJ_{k}^{{}}}}{{R_{k}^{4}}}{\text{,}}\quad k = {\text{1,3,}}\quad {{G}_{t}} = \frac{{EJ_{t}^{{}}}}{{2\left( {1 + \mu {\text{ }}} \right)R_{k}^{4}}}.$

Кольцо характеризуется параметрами: R_k – радиус центра масс сечения кольца; Е – комплексный модуль упругости материала; ${{\rho }_{*}}$ – плотность материала; F – площадь поперечного сечения; J₁ и J₃ – моменты инерции поперечного сечения; J₁₃ – центробежный момент инерции; J_t – массовый момент инерции при кручении. На кольцах могут быть упруго закреплены сосредоточенные массы $m_{u}^{\partial }$, $m_{w}^{\partial }$, C_u, C_w – жесткости их крепления. Массы m^∂, $m_{w}^{\partial }$ и жесткости C_u, C_w моделируют виброизолированное оборудование, установленное на кольцах.

Приведение перемещений и внутренних сил на концах оболочек к кольцу. В случае, когда к кольцу (слева и справа) крепятся оболочки разного диаметра необходимо выполнить соответствующее приведение координат (перемещений) торцов оболочек к центру масс поперечного сечения кольца.

Векторы перемещений концевых сечений оболочки

$\zeta _{{k1}}^{{}} = H_{k}^{1}{{Z}_{k}},\quad \zeta _{{k + 1,0}}^{{}} = H_{k}^{2}Z_{k}^{{}},\quad {{Z}_{k}} = {{\left\{ {{{U}_{k}},{{V}_{k}},{{W}_{k}},\theta {{R}_{k}}} \right\}}^{Т}},$

где $H_{k}^{1}$ и $H_{k}^{2}$ – матрицы приведения координат концевых сечений оболочки к кольцу; Z_k – вектор перемещений кольца

$H_{k}^{{\text{1}}} = \left\| {{\text{ }}\begin{array}{*{20}{c}} {\text{1}}&{\text{0}}&{\text{0}}&0 \\ {\text{0}}&1&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{1}}&0 \\ {\text{0}}&{\text{0}}&{\text{0}}&{\frac{{{{r}_{k}}}}{{{{R}_{k}}}}} \end{array}{\text{ }}} \right\|,\quad H_{k}^{{\text{2}}} = \left\| {{\text{ }}\begin{array}{*{20}{c}} {\text{1}}&{\text{0}}&{\text{0}}&0 \\ {\text{0}}&1&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{1}}&0 \\ {\text{0}}&{\text{0}}&{\text{0}}&{\frac{{{{r}_{{k + 1}}}}}{{{{R}_{k}}}}} \end{array}{\text{ }}} \right\|.$

Внутренние силы, действующие в торцевых сечениях оболочек (в конце предыдущей оболочки η_k, 1 и в начале последующей оболочки η_k _+ 1, 0), приведем к соединяющему их кольцу с помощью матриц приведения $H_{k}^{3}$ и $H_{k}^{4}$.

Матрицы преобразования сил, действующих на концы оболочек номер k и k + 1 к центру масс сечения кольца номер k

(15)

$\begin{gathered} f_{k}^{1} = H_{k}^{3}\eta _{{k1}}^{{}},\quad f_{k}^{2} = H_{k}^{4}\eta _{{k + 1,0}}^{{}},\quad \eta _{{k0}}^{{}} = \eta _{k}^{{}}\left( 0 \right),\quad \eta _{{k1}}^{{}} = \eta _{k}^{{}}\left( {{{\ell }_{k}}} \right), \\ H_{k}^{3} = \left\| {{\text{ }}\begin{array}{*{20}{c}} {\frac{{{{r}_{k}}}}{{{{R}_{k}}}}}&{\text{0}}&{\text{0}}&0 \\ {\text{0}}&{\frac{{{{r}_{k}}}}{{{{R}_{k}}}}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\frac{{{{r}_{k}}}}{{{{R}_{k}}}}}&{\text{0}} \\ {\frac{{\left( {{{R}_{k}} - {{r}_{k}}} \right){{r}_{k}}}}{{R_{k}^{2}}}}&{\text{0}}&0&{\frac{{r_{k}^{2}}}{{R_{k}^{2}}}} \end{array}{\text{ }}} \right\|,\quad H_{k}^{4} = \left\| {{\text{ }}\begin{array}{*{20}{c}} {\frac{{{{r}_{{k + 1}}}}}{{{{R}_{k}}}}}&{\text{0}}&{\text{0}}&0 \\ {\text{0}}&{\frac{{{{r}_{{k + 1}}}}}{{{{R}_{k}}}}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\frac{{{{r}_{{k + 1}}}}}{{{{R}_{k}}}}}&{\text{0}} \\ {\frac{{\left( {{{R}_{k}} - {{r}_{{k + 1}}}} \right){{r}_{{k + 1}}}}}{{R_{k}^{2}}}}&{\text{0}}&0&{\frac{{r_{{k + 1}}^{2}}}{{R_{k}^{2}}}} \end{array}{\text{ }}} \right\|. \\ \end{gathered} $

Уравнение движения центра масс сечения k-го кольца имеет вид

(16)

$M_{k}^{{}}Z_{k}^{{}} = {{P}_{k}} - f_{k}^{1} + f_{k}^{2}.$

Подставляя в уравнение движения кольца (16) выражения (8, 11, 12–15) получим систему уравнений относительно векторов Z_k: порядка 4(N + 1), где N – количество оболочек; N + 1 – количество колец. Уравнения (16) составляются для каждого кольца последовательно

$\left[ {{{M}_{0}} - H_{0}^{4}G_{1}^{*}\left( 0 \right){{B}_{{{\text{1}}{\text{.1}}}}}H_{0}^{2}} \right]{{{\text{Z}}}_{{\text{0}}}} - H_{0}^{4}G_{1}^{*}\left( 0 \right){{B}_{{{\text{2}}{\text{.1}}}}}H_{1}^{1}{{Z}_{1}} = $

$ = {{P}_{1}} + H_{0}^{4}\left\{ {{{\Phi }_{1}}W_{1}^{*} - G_{1}^{*}\left( 0 \right)\left[ {{{B}_{{1.1}}}\zeta _{1}^{*} + {{B}_{{2.1}}}\zeta _{1}^{*}{{e}^{{i{{\theta }_{1}}{{\ell }_{1}}}}}} \right]} \right\},$

$H_{k}^{3}G_{k}^{*}\left( {{{\ell }_{k}}} \right){{B}_{{{\text{1,k}}}}}H_{{k - 1}}^{2}{{Z}_{{k - 1}}} + \left[ {{{M}_{k}} + H_{k}^{3}G_{k}^{*}({{\ell }_{n}}){{B}_{{2,k}}}H_{k}^{1} - H_{k}^{4}G_{{k + 1}}^{*}(0){{B}_{{1,k = 1}}}H_{k}^{2}} \right]{{Z}_{k}} - $

(17)

$ - \;H_{k}^{4}G_{{k + 1}}^{*}(0){{B}_{{2,k + 1}}}H_{{k + 1}}^{1}{{Z}_{{k + 1}}} = {{P}_{k}} + \left\{ {H{}_{k}^{4}{{\Phi }_{{k + 1}}}W_{{k + 1}}^{*} - H_{k}^{3}{{\Phi }_{k}}W_{k}^{*}{{e}^{{i{{\theta }_{k}}{{\ell }_{k}}}}} + } \right.$

$ + \;H_{k}^{3}G_{k}^{*}({{\ell }_{k}})\left[ {{{B}_{{1,k}}}\zeta _{k}^{*} + B_{{2,k}}^{{}}\zeta _{k}^{*}{{e}^{{i{{\theta }_{k}}{{\ell }_{k}}}}}} \right] - H_{k}^{4}G_{{k + 1}}^{*}(0)\left. {\left[ {{{B}_{{1,k + 1}}}\zeta _{{k + 1}}^{*} + {{B}_{{2,k + 1}}}\zeta _{{k + 1}}^{*}{{e}^{{i{{\theta }_{k}}{{\ell }_{k}}}}}} \right]} \right\},$

$H_{n}^{3}G_{n}^{*}\left( {{{\ell }_{n}}} \right){{B}_{{1,n}}}H_{{n - 1}}^{2}{{z}_{{n - 1}}} + \left[ {{{M}_{n}} + H_{n}^{3}G_{n}^{*}({{\ell }_{n}}){{B}_{{2,n}}}H_{n}^{1}} \right]{{Z}_{n}} = $

$ = {{P}_{n}} + H_{n}^{3}{{\Phi }_{n}}W_{n}^{*}{{e}^{{i{{\theta }_{n}}{{\ell }_{n}}}}} - H_{n}^{3}G_{n}^{*}\left( {{{\ell }_{n}}} \right)\left[ {{{B}_{{1,n}}}\zeta _{n}^{*} + {{B}_{{2,n}}}\zeta _{n}^{*}{{e}^{{i{{\theta }_{n}}{{\ell }_{n}}}}}} \right].$

Здесь первое уравнение составлено для первого кольца, соединенного с оболочкой справа, второе уравнение – для промежуточного кольца, соединенного с оболочками слева и справа, а третье – для последнего кольца, соединенного с оболочкой слева.

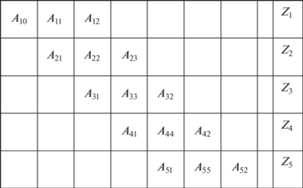
Общее матричное уравнение вынужденных колебаний составной оболочки имеет ленточной вид цепной системы. Уравнение состоит из блок-матриц четвертого порядка, квазидиагонально расположенных. На рис. 2 показана структура матричного уравнения составной оболочки с четырьмя оболочками и пятью кольцами, где крайние блоки А₁₀ = 0 и А₅₂ = 0, потому что перед первым кольцом и после последнего кольца нет оболочек. Такая ленточная структура позволяет быстро решать матричные уравнения высокого порядка (нескольких сотен). В результате решения этой системы определяются искомые векторы перемещений колец Z_k.

Рис. 2.

Структура матричного уравнения.

После определения векторов перемещений Z_k на кольцах k из уравнения (17) можно определить амплитудно-частотные характеристики колебаний составной оболочки в заданных сечениях (кольцах) оболочечной конструкции, а также формы вынужденных колебаний составной оболочки в целом.

Заключение. Предложен метод расчета вынужденных колебаний составной оболочки со свободными граничными условиями, включающей соединенные между собой цилиндрические оболочки и упругие кольца, возбуждаемые совместно сосредоточенными и распределенными нагрузками. По отношению к методу [3], где возбуждение задавалось дискретными силами, приложенными к кольцам, метод расширен и дополнен возможностью расчета вынужденных колебаний составной оболочечной системы дискретными силами и динамическим давлением, приложенным к оболочке, что делает метод более универсальным. Дополнительный уточняющий учет возбуждения колебаний оболочки от давления через сжимаемую среду определяет новизну и полезность разработки.

Список литературы

Шендеров Е.Л. Волновые задачи гидроакустики. Л.: Судостроение, 1972. 349 с.
Романов В.Н., Иванов В.С. Излучение звука элементами судовых конструкций. СПб.: Судостроение, 1993. 212 с.
Косарев О.И. Вынужденные колебания цилиндрической оболочки, погруженной в жидкость // Проблемы машиностроения и надежности машин. 2020. № 2. С. 16.
Бидерман В.Л. Механика тонкостенных конструкций. Статика. М.: Машиностроение, 1977. С. 260.
Прочность. Устойчивость. Колебания. Том 3. Справочник / Под ред. И.А. Биргера и Я.Г. Пановко. М.: Машиностроение, 1968. С. 423.
Авербух А.З., Вейцман Р.И., Генкин М.Д. Колебания элементов конструкций в жидкости. М.: Наука, 1987. 158 с.
Абрамов А.А., Конюхова Е.Б., Парийский Б.С. Численные исследования свободных и вынужденных колебаний в сжимаемой среде замкнутых упругих моментных оболочек вращения // Журнал вычислительной математики м математической физики. 1989. Т. 29. № 5. С. 747.
Косарев О.И. Дисперсионное уравнение свободной конечной цилиндрической оболочки, погруженной в жидкость // Проблемы машиностроения и надежности машин. 2019. № 5. С. 36.
Balena F.J., Prydz R.A., Revell J.D. Single and doublewall cylinder noise reduction // J. Airocraft. 1983. V. 20. № 5. P. 434.
Shenck H.A. The efficient calculation and display of dispersion curves for a thin cylindrical shell immersed in a fluid // Proc. ICA 14. 1992. Paper B8-2.
Shvartz A., Samsonov A., Dreiden G, Semenova I. Evolution of bulk stain solution in cylindrical in homogeneus shells // AIP Conf. Proc. 2015. V. 1685.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал