Проблемы машиностроения и надежности машин, 2023, № 1, стр. 26-37

Вращение ротора часто сопровождается различными, в том числе, и нелинейными эффектами, связанными с гироскопическими и аэрогидродинамическими силами, геометрическими особенностями вала, с взаимодействием с опорами, приводным двигателем и др. [1–6]. Отметим существенное влияние внутреннего трения, которое является дестабилизирующим фактором, вызывающим неустойчивость вращения ротора [5, 7–9]. Динамическая неустойчивость ротора проявляется в виде нарастающих колебаний оси ротора и особенностей прецессии [10–12]. Прецессия оси гибкого ротора обычно является крайне нежелательным явлением, приводящим к возможным контактным взаимодействиям с элементами статора. Особенности прецессионного движения при контакте с элементами жесткого или податливого статора рассматривались в работах [3–5, 13–20]. В частности, в статьях [3, 16–20] был выявлен режим обратной прецессии при обкатке ротора внутри статора за счет сухого трения. Показано, что существует предельная скорость обкатки, равная собственной частоте ротора [3]. В работе [4] исследованы контактные режимы ротора с элементами роторной системы в двух различных ситуациях: а) контакт ротора с неподвижным статором; б) контакт ротора с легкими подвижными элементами (уплотнительными кольцами, упругими опорами и т.д.). При анизотропной опоре возникает двуударный режим ротора, который может происходить как в плоскости наименьшей, так и наибольшей жесткости, в зависимости от соотношения масс ротора и опоры. Установлено, что анизотропия жесткости опор и внешнего трения приводит к взаимодействию прямой и обратной прецессии [4]. Прецессия ротора на анизотропных опорах представляет собой эллиптическую кривую, вследствие наложения прямой и обратной прецессии [5].

В этих работах показано, что при контакте вращающегося ротора с элементами кольцевого статора возможны различные типы движения (периодические, почти периодические, хаотические), сопровождающиеся ударами различной кратности. В статье [21] было рассмотрено поведение ротора типа Джеффкотта при контакте диска с одним упругим ограничителем, где установлено, что в докритической области при контакте ротора с ограничителем в зависимости от величины зазора и угловой скорости вращения ротора могут возникнуть периодические однократные или трехкратные контакты с опорой. В закритической области контакт ротора с ограничителем стабилизирует амплитуды его колебаний. При этом в зависимости от величины эксцентриситета массы диска в закритической области возможны различные прецессионные вибрации.

Настоящая статья посвящена анализу динамики прецессирующего гибкого ротора с внутренним трением в закритической области скорости вращения и стабилизации его поперечных колебаний за счет взаимодействия с точечными вязкоупругими опорами – ограничителями, установленными с радиальным зазором в плоскости диска.

Расчетная схема. Ротор представляет собой гибкий вал постоянного круглого поперечного сечения с массивным однородным диском массой М и диаметром D, закрепленным на одном из концов вала. Другой конец вала установлен в жесткой опоре по типу “заделки” (рис. 1а). Погонная масса вала m_R равномерно распределена по его длине l. Диск обладает эксцентриситетом массы $e \ll D$.

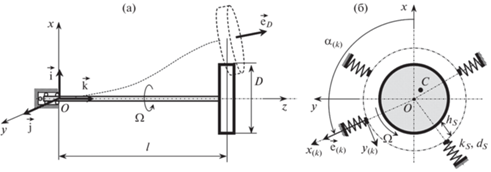
Ротор вращается вокруг своей продольной оси с постоянной угловой скоростью Ω. Учитывается внутреннее трение в материале вала, пропорциональное скорости его деформации, а также внешнее линейное демпфирование, пропорциональное абсолютной скорости ротора. Движение ротора рассматривается относительно неподвижной правосторонней системы координат Oxyz с началом в опоре ротора. Ось Oz совпадает с продольной осью недеформированного ротора; оси Ox и Oy взаимно перпендикулярны оси Oz (рис. 1а). Орты ${\mathbf{\vec {i}}}$, ${\mathbf{\vec {j}}}$, ${\mathbf{\vec {k}}}$¹¹ связаны с осями Oxyz; орт ${{{\mathbf{\vec {e}}}}_{D}}$ связан с центральным сечением диска и направлен по нормали к его плоскости (по локальной касательной к оси вала).

Для ограничения изгибных колебаний ротора в диаметральной плоскости диска по направлениям векторов ${{{\mathbf{\vec {e}}}}_{{\left( k \right)}}}$ = $\cos \left( {{{\alpha }_{{\left( k \right)}}}} \right){\mathbf{\vec {i}}}$ + $\sin \left( {{{\alpha }_{{\left( k \right)}}}} \right){\mathbf{\vec {j}}}$, ${{\alpha }_{{\left( k \right)}}}$ = $\angle \left( {x,{{x}_{{\left( k \right)}}}} \right)$, установлены $k\, = \,\overline {1,\,{{N}_{S}}} $ одинаковых вязкоупругих опор с линейной жесткостью ${{k}_{{\left( k \right)}}}$ и коэффициентом демпфирования ${{d}_{{\left( k \right)}}}$, которые могут деформироваться вдоль направления $O{{x}_{{\left( k \right)}}}$ (рис. 1б). Контактная поверхность опор расположена на расстоянии ${{h}_{{\left( k \right)}}}$ по нормали к окружной поверхности диска. Массой ограничителей пренебрегаем, что предполагает безударный контакт. Задача сводится к исследованию влияния внутреннего трения вала, дисбаланса диска и параметров ограничителей (установочного зазора, жесткости, демпфирования и коэффициента трения скольжения) на особенности прецессионного вращения ротора.

Уравнения движения ротора. Положение и угол поворота оси ротора в системе координат Oxyz будем описывать векторами ${\mathbf{r}}\left( {z,t} \right)$ = ${{\left\{ {{{u}_{x}}\left( {z,t} \right),{{u}_{y}}\left( {z,t} \right)} \right\}}^{T}}$ и $\vartheta \left( {z,t} \right)$ = = ${{\left\{ {{{\vartheta }_{x}}\left( {z,t} \right),{{\vartheta }_{y}}\left( {z,t} \right)} \right\}}^{T}}$. При вращении ротора на диск действуют внешняя сила ${{{\mathbf{P}}}_{{D\,{\text{ext}}}}}\left( t \right)$ и внешний момент ${{{\mathbf{L}}}_{{D\,{\text{ext}}}}}\left( t \right)$; здесь и ниже по тексту индекс D приписан к параметрам диска.

Внешняя сила включает в себя: 1) силу трения о внешнюю среду ${{{\mathbf{P}}}_{{Dd}}}\left( t \right)$ = $ - {{d}_{{Dr}}}{{{\mathbf{\dot {r}}}}_{D}}\left( t \right)$, ${{d}_{{Dr}}}$ – коэффициент внешнего линейного трения; 2) силу веса (в случае горизонтальной оси ротора) ${{{\mathbf{P}}}_{{Dg}}} = - Mg{\mathbf{i}}$, ${\mathbf{i}} = {{\left\{ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right\}}^{T}}$; 3) силу от дисбаланса диска ${{{\mathbf{P}}}_{{De}}}\left( t \right)$ = $Me{{\Omega }^{2}}{\mathbf{c}}\left( t \right)$, ${\mathbf{c}}\left( t \right)$ = ${{\left\{ {\cos \left( {\Omega t + {{\varphi }_{e}}} \right),\sin \left( {\Omega t + {{\varphi }_{e}}} \right)} \right\}}^{T}}$, ${{\varphi }_{e}}$ – произвольная начальная фаза; 4) суммарную силу взаимодействия диска с системой точечных вязкоупругих безмассовых опор ${{{\mathbf{F}}}_{{D\Sigma }}}\left( t \right)$, которая будет описана ниже; 5) силу действия на диск со стороны вала ${{{\mathbf{P}}}_{{DR}}}\left( t \right)$

При формировании внешнего момента ограничимся моментом, вызванным внешним трением, которое пропорционально скорости угловых поворотов относительно поперечных осей диска, а также моментом ${{{\mathbf{L}}}_{{DR}}}\left( t \right)$, действующим на диск со стороны вала ротора

Уравнения Ньютона–Эйлера для диска принимают вид

где $2\Omega B{\mathbf{S}}{{\dot {\vartheta }}_{D}}\left( t \right)$ – гироскопический момент вращающегося диска, $B = {{M{{D}^{2}}} \mathord{\left/ {\vphantom {{M{{D}^{2}}} {16}}} \right. \kern-0em} {16}}$ – момент инерции диска вокруг поперечных осей.

Уравнения движения вала ротора под действием распределенной поперечной нагрузки ${\mathbf{q}}\left( {z,\,t} \right)$ и распределенной моментной изгибающей нагрузки ${\mathbf{m}}\left( {z,\,t} \right)$ для модели стержня Бернулли–Эйлера запишем в векторно-матричной форме

где ${\mathbf{Q}}\left( {z,t} \right)$, ${\mathbf{M}}\left( {z,t} \right)$ – векторы поперечной силы и изгибающего момента в текущем сечении вала; ρ_R – плотность материала вала; I_R – геометрический момент инерции поперечного сечения вала относительно поперечной оси; “штрихом” обозначена операция дифференцирования по координате z.

Влияние диска учитывается введением в распределенные нагрузки ${\mathbf{q}}\left( {z,t} \right)$, ${\mathbf{m}}\left( {z,t} \right)$ сосредоточенной силы ${{{\mathbf{P}}}_{{RD}}} = - {{{\mathbf{P}}}_{{DR}}}$ и сосредоточенного изгибающего момента ${{{\mathbf{L}}}_{{RD}}} = - {{{\mathbf{L}}}_{{DR}}}$ с помощью дельта-функции Дирака $\delta \left( {z - {{z}_{D}}} \right)$. Таким образом, распределенные нагрузки

где d_e – коэффициент внешнего демпфирования вала; ${{T}_{V}}$ – коэффициент, характеризующий внутреннее трение в материале вала (время релаксации в законе Фойгта); $E{{I}_{R}}$ – изгибная жесткость вала.

Учитывая, что $\vartheta = - {\mathbf{Sr}}{\kern 1pt} '$ и ${\mathbf{M}} = E{{I}_{R}}\vartheta {\kern 1pt} '$, после преобразований системы (4), получим уравнение четвертого порядка относительно вектора ${\mathbf{r}}\left( {z,\,t} \right)$

Приведенные уравнения движения аналогичны полученным другими авторами, например, в книге [5]. Однако настоящая форма записи уравнений (6), позволяет при их численном решении более наглядно проанализировать влияние всех учитываемых силовых факторов на движение ротора при взаимодействии с дополнительными опорами.

Приведем уравнения (6) к безразмерному виду, используя линейный масштаб ${{Z}_{*}}$ и масштаб времени ${{T}_{*}}$: $z = {{Z}_{*}}\zeta $, $t = {{T}_{*}}\tau $, причем ${{Z}_{*}}$ = l ${{T}_{*}} = \sqrt {{{M{{l}^{3}}} \mathord{\left/ {\vphantom {{M{{l}^{3}}} {E{{I}_{R}}}}} \right. \kern-0em} {E{{I}_{R}}}}} $. Кроме того, введем безразмерные прогиб и поворот оси вала (поперечного сечения) ${\mathbf{\xi }}\left( {z,t} \right) = {{{\mathbf{r}}\left( {z,t} \right)} \mathord{\left/ {\vphantom {{{\mathbf{r}}\left( {z,t} \right)} l}} \right. \kern-0em} l}$, $\vartheta \left( {z,t} \right) = - {\mathbf{S\xi }}{\kern 1pt} '\left( {z,t} \right)$. Используем также обозначения для производных $\forall a$, a' = = ${{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial \zeta }}} \right. \kern-0em} {\partial \zeta }} = l{{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial z}}} \right. \kern-0em} {\partial z}}$, $\dot {a} = {{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}$ = $\sqrt {{{M{{l}^{3}}} \mathord{\left/ {\vphantom {{M{{l}^{3}}} {E{{I}_{R}}}}} \right. \kern-0em} {E{{I}_{R}}}}} {{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial t}}} \right. \kern-0em} {\partial t}}$. Тогда в уравнениях (6) образуются следующие безразмерные комплексы – критерии подобия (обозначены греческими буквами)

где ${{\varepsilon }_{D}}$ – относительный диаметр диска (диаметр, отнесенный к длине ротора), N – угловая скорость вращения ротора.

Учитывая подстановки ${\mathbf{m}} \leftarrow \left( {{{{{l}^{2}}} \mathord{\left/ {\vphantom {{{{l}^{2}}} {E{{I}_{R}}}}} \right. \kern-0em} {E{{I}_{R}}}}} \right){\mathbf{m}}$, ${\mathbf{q}} \leftarrow \left( {{{{{l}^{3}}} \mathord{\left/ {\vphantom {{{{l}^{3}}} {E{{I}_{R}}}}} \right. \kern-0em} {E{{I}_{R}}}}} \right){\mathbf{q}}$, получим уравнения движения ротора в следующей безразмерной форме

где здесь ${{{\mathbf{q}}}_{V}}\left( {\zeta ,\tau } \right)$ – распределенная поперечная нагрузка от сил внутреннего трения в материале вала.

Взаимодействие ротора (диска) с ограничителями. Каждая из ${{N}_{S}}$ упруго-демпферных опор, обладающих линейной жесткостью ${{\kappa }_{{\left( j \right)}}} = \left( {{{{{k}_{{\left( j \right)}}}l} \mathord{\left/ {\vphantom {{{{k}_{{\left( j \right)}}}l} {E{{I}_{R}}}}} \right. \kern-0em} {E{{I}_{R}}}}} \right)$ и коэффициентом демпфирования ${{\eta }_{{\left( j \right)}}}$ = ${{d}_{{\left( j \right)}}}\sqrt {{{{{l}^{3}}} \mathord{\left/ {\vphantom {{{{l}^{3}}} {\left( {ME{{I}_{R}}} \right)}}} \right. \kern-0em} {\left( {ME{{I}_{R}}} \right)}}} $, расположена на расстоянии ${{\chi }_{{\left( j \right)}}} = {{{{h}_{{\left( j \right)}}}} \mathord{\left/ {\vphantom {{{{h}_{{\left( j \right)}}}} l}} \right. \kern-0em} l}$, $j = \overline {1,{{N}_{s}}} $ от периферийный поверхностности диска. Опора может деформироваться только вдоль направления $O{{x}_{{\left( j \right)}}}$. При контакте ротора с опорой в распределенной нагрузке ${{{\mathbf{q}}}_{\xi }}\left( {\zeta ,\,\tau } \right)$, входящей в безразмерные уравнения (9), необходимо добавить сосредоточенную силу действия j-й опоры на диск ${{\Psi }_{{\left( j \right)}}}\left( \tau \right)$ = $\left\{ {{{\Psi }_{{x\left( j \right)}}}\left( \tau \right)} \right.$, ${{\left. {{{\Psi }_{{y\left( j \right)}}}\left( \tau \right)} \right\}}^{T}}$, которая содержит две компоненты – нормальную, вдоль оси $O{{x}_{{\left( j \right)}}}$, и тангенциальную к поверхности опоры (сила трения с коэффициентом ${{f}_{S}}$) вдоль оси $O{{y}_{{\left( j \right)}}}$. Силу взаимодействия ротора с упруго-демпфированной опорой будем описывать формулами

где ${\rm H}\left( {{{\xi }_{x}}_{{\left( k \right)}}\, - \,{{\chi }_{{\left( k \right)}}}} \right)$ – функция Хэвисайда, которая равна единице, если диск внедрен в одностороннюю опору – $\left( {{{\xi }_{x}}_{{\left( k \right)}} - {{\chi }_{{\left( k \right)}}}} \right) > 0$, ${\rm H}\left( {{{r}_{{\left( k \right)}}}} \right)$ – опора работает, если существует только нормальная сила давления на контактные поверхности, ${{r}_{{\left( k \right)}}}\,$ – нормальная контактная сила, ${{{\mathbf{s}}}_{{\left( k \right)}}}$ – вектор распределения сил на опоре, ${{V}_{{\left( k \right)}}}$ – скорость скольжения поверхности диска относительно поверхности k-й опоры. В результате суммарная сила от взаимодействия со всеми опорами ${{{\mathbf{\Psi }}}_{{D\Sigma }}}$ = $\sum\nolimits_{k = 1}^{{{N}_{s}}} {{{{\mathbf{\Psi }}}_{{\left( k \right)xy}}}} $.

Влияние эксцентриситета массы и силы веса диска. При наличии эксцентриситета $\varepsilon = {e \mathord{\left/ {\vphantom {e l}} \right. \kern-0em} l}$ в векторе ${{{\mathbf{q}}}_{\xi }}\left( {\zeta ,\,\tau } \right)$ и, соответственно, в безразмерных уравнениях движения, необходимо учитывать дополнительную компоненту ${{\Pi }_{{De}}}$ поперечной сосредоточенной силы ${{{\mathbf{\Pi }}}_{\Sigma }}$, входящую в выражение (9)

где $\varphi $ – произвольная начальная фаза. В случае горизонтального расположения ротора учитывается сила веса диска ${{{\mathbf{\Pi }}}_{{Dg}}} = - \gamma {\mathbf{i}}$. В результате суммарного действия сосредоточенных сил ${{{\mathbf{\Pi }}}_{{De}}}\left( \tau \right)$ и ${{{\mathbf{\Pi }}}_{{Dg}}}$сосредоточенная сила ${{{\mathbf{\Pi }}}_{\Sigma }}\left( \tau \right)$ принимает вид

Интегральная форма решения. Решение уравнений (8) с учетом (2) и (11) будем искать как решение интегрального уравнения Фредгольма второго рода с помощью функции Грина $G\left( {\zeta ,s} \right)$ для стержня Бернулли–Эйлера

В дальнейшем используются обозначения для частных производных функции Грина ${{G}_{{,kl}}}\left( {\zeta ,s} \right)$ = ${{{{\partial }^{k}}{{\partial }^{l}}G\left( {\zeta ,s} \right)} \mathord{\left/ {\vphantom {{{{\partial }^{k}}{{\partial }^{l}}G\left( {\zeta ,s} \right)} {\partial {{\zeta }^{k}}\partial {{s}^{l}}}}} \right. \kern-0em} {\partial {{\zeta }^{k}}\partial {{s}^{l}}}}$. При подстановке (13) в уравнения (8) получим

где функция Грина для консольно закрепленного ротора равна

Последующее решение сводится к вычислению интегралов, входящих в (14), например, приближенно по методу трапеций для m узлов коллокации. В результате исходные уравнения в частных производных сводятся к системе обыкновенных дифференциальных уравнений относительно независимых переменных. После вычисления корней характеристического уравнения и определения бифуркации Пуанкаре–Андронова–Хопфа устанавливается значение критической скорости вращения ротора ${{{\text{N}}}_{{{\text{crit}}}}}$ в зависимости от параметров системы, при которой возникает потеря устойчивости прямолинейного вращения ротора при отсутствии контакта с опорами.

Условия потери устойчивости за счет внутреннего трения были подробно описаны в [5, 11].

При численном решении были использованы следующие базовые значения параметров²²: длина ротора $l = 0.7$ м, диаметр вала $d = 0.02$ м, диаметр диска $D = 0.2$ м, толщина диска $a = 0.01$ м, эксцентриситет массы, $e = 0.001$ м (ε = 0.00142), коэффициенты внутреннего и внешнего трения вала ${{\eta }_{i}} = 0.005$, ${{\eta }_{e}} = 0.025$, коэффициенты внешнего и линейного и углового демпфирования диска ${{\eta }_{{D\xi }}} = 0.0025$, ${{\eta }_{{D\vartheta }}} = 0.05$, установочный зазор опор ${{h}_{{\left( j \right)}}} = 0.0075$ м (${{{{\chi }}}_{{\left( j \right)}}}$ = 0.0107), коэффициенты жесткости и демпфирования опоры ${{k}_{S}} = 4.087 \times {{10}^{6}}$ Н/м ($\kappa = 850$) и ${{\eta }_{{\left( j \right)}}} = 0.06$, коэффициент трения скольжения на опоре ${{f}_{S}} = 0.1$. В настоящей статье из-за несущественного влияния на динамику ротора пренебрегаем его силой веса.

В расчетах учитывались три одинаковых опоры, установленные под углом 2π/3 друг к другу, причем первая опора была установлена под углом ${{\alpha }_{1}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ к оси Ox. Такое расположение опор обеспечивает равные условия взаимодействия при контакте с ротором. Указанный алгоритм был реализован в комплексе MATLAB с использованием решателя ode23t (метод трапеций с интерполяцией), значения абсолютной и относительной ошибок AbsTol = RelTol = 10^–7.

Критическая скорость вращения ротора. Единственной причиной потери устойчивости является наличие силы внутреннего трения в материале вала, которые приводят к циркуляционным силам. Критическую угловую скорость вращения ротора ${\text{N}} = {{{\text{N}}}_{{{\text{crit}}}}}$ в зависимости от коэффициента внутреннего трения (рис. 2а) можно аппроксимировать функцией ${{{\rm N}}_{{{\text{crit}}}}}$ = $a\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}} + b$, где ${{\eta }_{e}}$, ${{\eta }_{i}}$ – коэффициенты внешнего и внутреннего трения (7), a и b – коэффициенты аппроксимации.

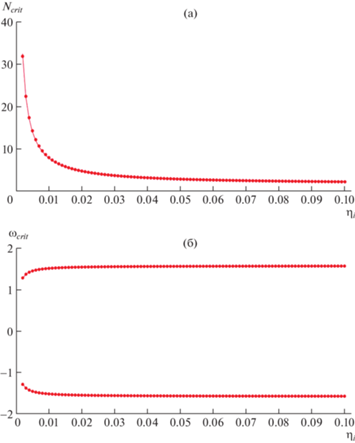
При этом критическая частота колебаний ротора ${{\omega }_{{{\text{crit}}}}}$ (мнимая часть характеристического показателя) линейно зависит от критической скорости вращения ротора ${{\omega }_{{{\text{crit}}}}} = {{{\rm N}}_{{{\text{crit}}}}}c + d$ = $ac\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}} + \left( {bc + d} \right)$ = $a{\kern 1pt} '\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}} + b{\kern 1pt} '$, $a{\kern 1pt} '\; = ac$, $b{\kern 1pt} '\; = bc + d$, где $a = 2.47$, $b = 1.64$, $a{\kern 1pt} ' = - 0.024$, $b{\kern 1pt} ' = \pm 1.58$.

Показатель прецессии. Прецессия центра вала в плоскости поперечного сечения диска может быть описана полярным вектором ${{{\mathbf{R}}}_{D}}\left( \tau \right)$ = ${{\left\{ {{{\xi }_{{Dx}}}\left( \tau \right),{{\xi }_{{Dy}}}\left( \tau \right)} \right\}}^{T}}$ с полярным углом $\tan \left( {\psi \left( \tau \right)} \right)$ = $\frac{{{{\xi }_{{Dy}}}\left( \tau \right)}}{{{{\xi }_{{Dx}}}\left( \tau \right)}}$, где переменные ${{{{\xi }}}_{{Dy}}}\left( {{\tau }} \right)$, ${{{{\xi }}}_{{Dx}}}\left( {{\tau }} \right)$ являются результатом численного расчета (или измерения) движения центра диска по двум ортогональным направлениям x, y. Угловая скорость прецессии при этом равна³³ ${{\dot {\psi }}}\left( {{\tau }} \right)$ = $\frac{{{{{\dot {\xi }}}_{{Dy}}}{{\xi }_{{Dx}}} - {{{\dot {\xi }}}_{{Dx}}}{{\xi }_{{Dy}}}}}{{\xi _{{Dx}}^{2} + \xi _{{Dy}}^{2}}}$.

Для оценки направления прецессии ротора будем использовать относительную угловую скорость прецессии $\Lambda \left( \tau \right)$ = ${{\dot {\psi }\left( \tau \right)} \mathord{\left/ {\vphantom {{\dot {\psi }\left( \tau \right)} {\rm N}}} \right. \kern-0em} {\rm N}}$, где скорость вращения задается с учетом принятого положительного направления вращения. Тогда знак относительной угловой скорости прецессии будет определять вид прецессии: прямую или обратную прецессию. Безразмерная (нормированная) частота колебаний относительной угловой скорости прецессии оси ротора ${{\nu }_{\Lambda }} = {\Lambda \mathord{\left/ {\vphantom {\Lambda {2\pi }}} \right. \kern-0em} {2\pi }}$, ${{\nu }_{{\rm N}}} = {{\rm N} \mathord{\left/ {\vphantom {{\rm N} {2\pi }}} \right. \kern-0em} {2\pi }}$ – безразмерная частота вращения вала ротора (ν, [Гц ${{T}_{*}}$], ${{T}_{*}}$ = 0.0226 с). Заметим, что в системе координат, вращающейся вместе с радиусом вектором, соединяющим неподвижный центр с центром вала, его материальное сечение поворачивается с угловой скоростью $\left( {{\rm N} - \dot {\psi }} \right)$. При прямой синхронной прецессии $\left( {\dot {\psi } = {\rm N},\Lambda = 1} \right)$ сечение остается неподвижным во вращающейся системе координат, обратная синхронная прецессия $\left( {{{\dot {\psi }}} = - {\rm N},\Lambda = - 1} \right)$ возникает тогда, когда в неподвижном базисе сечение вала совершает только поступательное движение.

Для произвольных движений ротора удобнее пользоваться средним по реализации значением относительной скорости прецессии $\bar {\Lambda } = \left\langle \Lambda \right\rangle $, знак которой является фактическим показателем прецессии: при $\bar {\Lambda } < 0$ – прямая прецессия, при $\bar {\Lambda } > 0$ – обратная прецессия, при $\left| {\bar {\Lambda }} \right| = 1$ – синхронная прецессия (прямая или обратная), $\left| {\bar {\Lambda }} \right| = 0$ – прецессия отсутствует.

Докритическое поведение ротора. Очевидно, что на докритических скоростях вращения и при наличии эксцентриситета $\varepsilon \ne 0$, когда отсутствует контакт с опорами, происходят моногармонические колебания ротора с прямой синхронной прецессией. При контакте несбалансированного ротора с опорами возникают нерегулярные неустановившиеся колебания. При этом относительная скорость прецессии Λ > 0 и наблюдается тенденция выхода на прямую прецессию.

Закритическое поведение. Закритическое вращение ротора с внутренним трением всегда сопровождается контактом с опорами независимо от величины зазора и внешнего демпфирования. На рис. 3а для случая ${\rm N} = 15 > {{{\rm N}}_{{{\text{crit}}}}}$, представлена диаграмма экстремумов радиальных перемещений диска EXTR$\left[ {{{\xi }_{{Dx}}}} \right]$ в направлении оси Ox при варьировании эксцентриситета массы (ε = 0–0.00143).

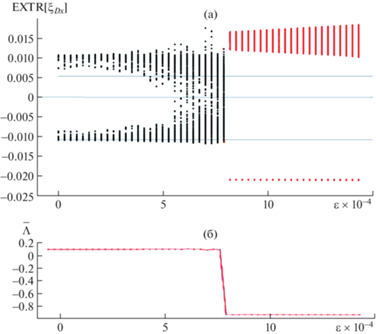
Черные точки соответствуют неустановившимся колебаниям с почти прямой прецессией $\overline \Lambda \approx 0.095 > 0$; красные точки соответствуют устойчивой обратной прецессии $\overline \Lambda \approx \, - \,0.93 < 0$. При значении $\varepsilon = {{\varepsilon }_{*}} \approx 0.0008$ меняется знак показателя прецессии ротора $\overline \Lambda $ (рис. 3б), что соответствует смене ее направления с прямой на обратную. Эта смена направления прецессии объясняется возрастанием сил трения при увеличении нормальных сил в контакте, что связано с увеличением неуравновешенности диска.

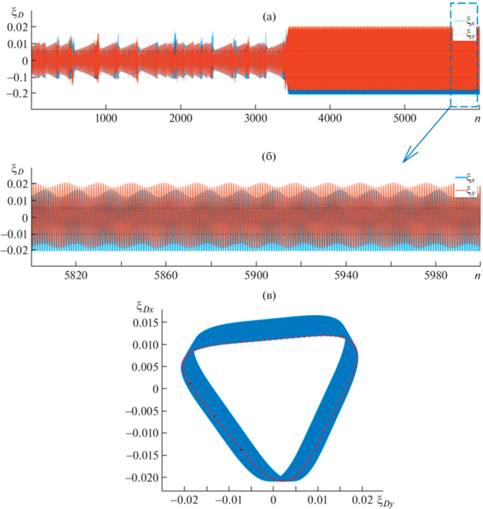
Рассмотрим две области ${{E}^{ - }} = \{ \varepsilon :0 < \varepsilon \leqslant {{\varepsilon }^{ - }}\} $, ${{E}^{ + }} = \{ \varepsilon :\varepsilon \geqslant {{\varepsilon }^{ + }}\} $. Как показали расчеты изменение в определенных пределах зазора между диском и коэффициента скольжения (трения) на опорах не приводит к переходу к обратной прецессии. Увеличение радиальной жесткости опор по сравнению с базовым значением позволяет стабилизировать движение ротора с прямой прецессией $(\overline \Lambda \approx 0.099)$. В области $\varepsilon \in {{E}^{ + }}$ наблюдается режим обратной прецессии $(\overline \Lambda \approx - 0.913)$, который можно поддержать варьированием параметрами опор (рис. 4). Красными точками на рис. 4б показано стробирование сигнала с частотой, соответствующей периоду вращения ротора (в данном случае – на последних 300-х оборотах).

На рис. 5а представлена временная реализация колебаний относительной угловой скорости прецессии $\Lambda (\tau )$ и ее частотный спектр (рис. 5б) при эксцентриситете ε = 0.00082.

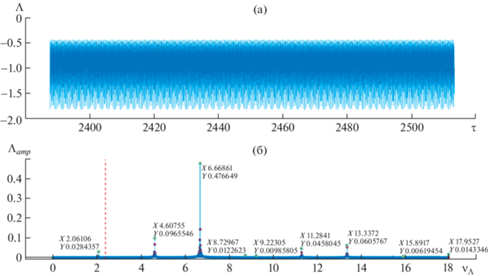
В спектре нормированной угловой частоты колебаний прецессии наблюдается пик $\Lambda (\tau )$ на частоте вращения вала ротора ${{\nu }_{\Lambda }}_{*} \approx 2.061$, которой соответствуют стробоскопические отметки, показанные красными точками на рис. 4. Наибольший пик возникает на частоте ${{\nu }_{\Lambda }} \approx 6.6686$ ≈ ${{N}_{S}}\bar {\Lambda }{{\nu }_{\Lambda }}_{*}$ (рис. 5б).

Кроме того, в данной системе при нулевом эксцентриситете существуют устойчивые чисто периодические движения. В частотном спектре существуют только две гармоники: на частотах ${{\nu }_{\Lambda }} \approx 6.6686$ ≈ ${{N}_{S}}\bar {\Lambda }{{\nu }_{\Lambda }}_{*}$ и ${{\nu }_{\Lambda }} \approx 13.3372$ ≈ $2{{N}_{S}}\bar {\Lambda }{{\nu }_{\Lambda }}_{*}$. При этом также поддерживается обратная прецессия $\overline \Lambda \approx - 0.931$.

При изменении скорости вращения Ν ротор проходит через область докритического вращения без взаимодействия с опорами (при выборе достаточно большого зазора) с прямой синхронной прецессией, а в области закритического вращения с взаимодействием с опорами – с устойчивой обратной прецессией.

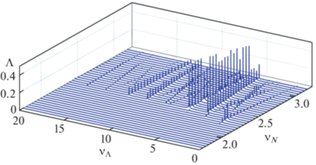
В качестве обобщения полученных численных результатов на рис. 6 представлен спектральный состав относительной угловой скорости прецессии ротора $\Lambda $ в зависимости от частоты вращения вала и частотного спектра частоты прецессии при взаимодействии с опорами.

На рис. 6 видно, как прямая синхронная прецессия скачком переходит к обратной прецессии при критической частоте вращения ротора ${{\nu }_{{{{{\rm N}}_{{{\text{crit}}}}}}}} \approx 2.35$ (все значения параметров ротора соответствуют базовым). Уменьшение частоты обратной прецессии с ростом закритической скорости вращения связано с тем, что происходит рост амплитуд ротора, рост сил нормального давления на опоры и, как следствие, увеличение тормозящих прецессию сил трения.

Заключение. Разработанная математическая модель ротора с массивным диском и внутренним трением позволяет исследовать закритическую динамику взаимодействия ротора с дискретно расположенными упруго демпфированными опорами. Введено определение относительной скорости прецессии ротора и ее показателя, позволяющие находить частоту прецессии и ее направление, для случая произвольной нелинейной динамики ротора. Показано, что в закритической области всегда существует уровень неуравновешенности ротора, при котором поддерживается устойчивая обратная прецессия, близкая к синхронной при квазипериодическом движении. Наибольшее влияние на стабилизацию обратной прецессии ротора оказывают эксцентриситет ротора и радиальная жесткость опор. При нулевом эксцентриситете возможно существование чисто периодического движения. Наибольшая частотная амплитуда колебаний прецессирующего ротора возникает на частоте прецессионного вращения, умноженной на количество установленных с начальным зазором упруго демпфированных опор. Изменение зазора между диском и дискретно расположенными опорами, как и изменение коэффициента трения скольжения (силы трения) на опорах в определенных пределах не приводят к переходу от неустойчивого, срывного характера движения, близкого к прямой прецессии, к устойчивой обратной прецессии. Изменение радиальной жесткости опор позволяет стабилизировать движение переходом к обратной прецессии.

Взаимодействие с опорами в зависимости от эксцентриситета массы ε может приводить к неустановившимся срывным колебаниям ротора при стремлении к прямой прецессии или – к устойчивому вращению с обратной прецессией.