Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 2, стр. 74-81

ВВЕДЕНИЕ

Впервые осцилляции интенсивности зеркального и дифрагированного пучков на картине дифракции быстрых электронов, полученной от растущей монокристаллической пленки, наблюдались в [1–3]. Период колебаний был равен времени напыления одного мономолекулярного слоя Ga + As толщиной с/2, где с – период решетки GaAs. Авторы [2] предположили, что эти осцилляции связаны с периодическим изменением шероховатости поверхности растущего кристалла, обусловленным формированием на атомарно гладкой поверхности двумерных зародышей, их разрастанием и объединением в сплошной монослой, образованием зародышей следующего слоя. В последующие годы была опубликована серия работ, в которых данное явление было изучено и использовано для исследования механизма и кинетики роста эпитаксиальных слоев [4–7].

Теоретическое объяснение осцилляций опиралось сначала на простые качественные модели [8–10]. Так, в [9] в кинематическом приближении рассмотрена интерференция пучков, отраженных от террас. Было получено выражение для интенсивности зеркального рефлекса:

где θ_n – покрытие n-го слоя, θ₀ = 1, φ – фазовый угол между террасами на соседних уровнях. Затем появились публикации, в которых количественно вычисляли интенсивности осцилляций зеркального рефлекса [11–16]. В них были воспроизведено поведение осцилляционных кривых. Однако, поскольку для интерпретации экспериментов в этих работах использованы численные расчеты, а не аналитические формулы, то, как отмечает автор [17], оставалось физически не ясным, почему в одной части кривой качания амплитуды осцилляции возрастают, а в другой убывают. Оставались трудности при интерпретации и некоторых других фактов, следующих из расчетов по алгоритмам, предложенным в [11]. В [18, 19] для интерпретации экспериментальных результатов использована модель [11]. По-видимому, получение аналитических выражений из первых принципов для описания реальной экспериментальной ситуации при эпитаксиальном росте пленок является трудно достижимой задачей. И в конкретных случаях можно пользоваться различными вычислительными алгоритмами и, в частности, достаточно “полным”, предложенным в [11], как это делают авторы [18, 19]. Однако остается справедливым замечание, сделанное выше.

В настоящей работе для теоретического описания осцилляций принята простая физическая модель процесса, приведены аналитические выражения, по которым выполнены расчеты, и графически проиллюстрированы их результаты. Использованные формулы просты и обладают наглядностью, позволяющей вскрывать природу возникновения осцилляций, которая может быть отлична от ранее принятой. В частности, показано, что при определенных условиях гетероэпитаксии период осцилляций может быть значительно больше времени роста одного монослоя пленки.

ВЫБОР МОДЕЛИ ПРОЦЕССА

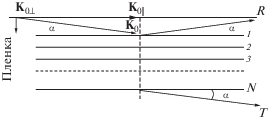
В [20] рассмотрен вопрос взаимодействия монохроматического пучка электронов средней или высокой энергии с тонкой монокристаллической пленкой при малом угле скольжения α (рис. 1). Благодаря малости этого угла энергия составляющей движения, нормальной к поверхности, мала и моделируется взаимодействием электронов низкой энергии с одномерным потенциалом пленки. В качестве модели потенциала кристаллической плоскости, параллельной поверхности пленки, выбрана δ-функция Дирака определенной “мощности”. Соответственно, одномерный потенциал всей пленки имеет вид конечной одномерной потенциальной “гребенки” из N δ-функций, где N – количество кристаллических плоскостей пленки, параллельных ее поверхности. Впервые для описания дифракции электронов на тонких монокристаллических пленках такой потенциал был выбран в [21]. Как отмечалось, он особенно удобен для учета границ пленки. В [20] было получено аналитическое выражение для коэффициентов прохождения T и отражения R электронов в зависимости от параметров модели (угла скольжения α, отражательной способности кристаллической плоскости U, периода одномерной решетки c, толщины пленки cN):

Там же были предложены два способа наблюдения квантового размерного эффекта в тонкой монокристаллической пленке.

Позднее [22] автором были получены уточняющие аналитические выражения для T и R, учитывающие скачок электростатического потенциала на границах пленки V₀, (т.е. с учетом среднего внутреннего потенциала кристалла) (рис. 2):

(значения символов k и μ объяснены ниже).

Далее рассмотрим подробнее, к примеру, выражение (2) (аналогичные рассуждения справедливы также и для формулы (1)). В [20, 22] для наблюдения квантового размерного эффекта было предложено варьировать угол скольжения α, от которого зависят значения k и μ. Но, как следует из формулы (2), квантовый размерный эффект может проявляться в осцилляциях интенсивности зеркально отраженного пучка и в зависимости от толщины пленки cN.

Здесь возникает одна тонкость. Так как толщина пленки реально всегда дискретна, то значения R можно получить только в N точках. Эту трудность можно обойти. Действительно, возьмем конкретный случай, когда происходит слоевой рост и площадь поверхности пленки толщиной cN постепенно уменьшается, а площадь поверхности пленки толщиной c(N + 1) увеличивается. В этом случае можно считать, что средняя толщина пленки плавно изменяется от значения cN до значения с(N + 1). Для описания этого процесса в формуле (2) можно варьировать N не дискретно, а непрерывно, считая, что N может иметь и дробную часть. Таким способом мы моделируем увеличение площади поверхности под электронным пучком в зависимости от пленки толщиной cN по мере ее зарастания новым монослоем до толщины c(N + 1). Ясно, что эти рассуждения можно применить и при наличии ступеней роста в количестве больше единицы. Аналогичный прием был применен в [11].

Из формулы (2) следует, что амплитуда осцилляций зависит от множителя в скобках перед ${{\sin }^{2}}\mu cN$ в знаменателе дроби, а он, в свою очередь, определяется нормальным волновым числом k, т.е. энергией электронов E и углом скольжения α, а также модулем блоховского волнового вектора μ, т.е. кристаллической структурой пленки. Период же осцилляций определяется множителем ${\text{si}}{{{\text{n}}}^{2}}{\mu }cN$ в знаменателе дроби, т.е. волновым числом μ и толщиной пленки $cN$. Он может принимать значения от нуля до бесконечности. Действительно, поскольку в разрешенной зоне $0 \leqslant {\mu } \leqslant {\pi \mathord{\left/ {\vphantom {\pi {c,}}} \right. \kern-0em} {c,}}$ то максимальный период $cN = \infty ,$ минимальный же период равен c. В самом деле, при ${\mu } = \frac{\pi }{c}{{\sin }^{2}}{\mu }cN = {{\sin }^{2}}\pi N.$ А поскольку период ${{\sin }^{2}}\pi N$ равен πn, где n = $0, \pm 1, \pm 2,...,$ то $\pi N = \pi n.$ При N = 1, 2, 3, … ${{\sin }^{2}}\pi N$ принимает одинаковые нулевые значения, т.е. минимальный период осцилляций равен c. Тот факт, что период в рассматриваемой модели может принимать произвольно большие значения, отличается от результатов ранее проведенных экспериментальных работ, в которых период всегда был равен толщине одного монослоя [23], т.е. в рассматриваемой модели равен c. Этот же результат следует из предыдущих теоретических работ (например, [24]).

Это несоответствие может быть объяснено следующим образом. Будем называть осцилляции с периодом, равным времени нарастания одного монослоя, коротковолновыми осцилляциями. Осцилляции же, обусловленные квантовым размерным эффектом и имеющие период больше одного монослоя, будем называть длинноволновыми. Будем считать, что коротковолновые осцилляции обусловлены рассеянием на поверхности роста, как это предполагалось, например, в [2], или интерференцией пучков, отраженных от террас [9], или механизмом, предложенным в [11,] и они присутствуют как при гомоэпитаксиальном, так и при гетероэпитаксиальном росте. Поэтому надо полагать, что длинноволновые осцилляции могут наблюдаться только при гетероэпитаксии и проявляться в модуляции коротковолновых осцилляций. Кстати, зависимости, которые, вероятно, должны иметь место, действительно наблюдались при эпитаксии Ni на W (рис. 6 и 7 в [25]). Только там они не получили верной интерпретации. А тот факт, что амплитуда модуляции затухает по мере роста толщины пленки, можно объяснить поглощением электронов, которое не было учтено при выводе формул (1) или (2). Ниже приводятся результаты расчетов по формуле (2) и их обсуждение в различных экспериментальных ситуациях.

КРАТКОЕ ИЗЛОЖЕНИЕ ВЫВОДА ОСНОВНОЙ ФОРМУЛЫ

Здесь кратко повторим вывод выражения (2). Подробные выкладки можно найти в [22]. Зависимость потенциальной энергии электрона от толщины пленки приведена на рис. 2. Соответственно, волновая функция частицы ψ(x) определяется решением стационарного уравнения Шредингера

с потенциальной энергией электрона V(x), задаваемой уравнениями:

Здесь с – период решетки, N – число периодов, ${{V}_{0}} > 0$ − высота потенциальной ступеньки на границах пленки, δ(x) – дельта-функция Дирака, U – “мощность” потенциала δ-функции, ħ – постоянная Планка, m – масса электрона.

В отличие от [20, 26–28], где формулы для коэффициентов T(α), R(α) выводили с помощью аппарата матриц сшивания и трансляционных матриц волновых функций свободных электронов, в настоящей работе сшиваются волновые функции в точках х₁ = –c/2, x₂ = cN – c/2. Внутри пленки волновая функция представляет собой суперпозицию двух блоховских волн, двигающихся навстречу друг другу. Их аналитические выражения для решетки из δ-функций впервые были получены в [28]:

где x' = x – c[x/c], [x/c] – целая часть значения выражения x/c; μ – модуль блоховского волнового вектора, определяемого из уравнения дисперсии: k – модуль волнового вектора свободного электрона.

Таким образом, волновая функция задачи имеет следующий вид: слева от пленки (рис. 2) – сумма падающей и отраженной волн свободных электронов:

Внутри пленки, используя уравнение дисперсии, получим:

справа от пленки

Здесь $\lambda = \sqrt {\frac{{2m{{E}_{1}}}}{{{{\hbar }^{2}}}}} ,$ $k = \sqrt {\frac{{2m({{E}_{1}} + {{V}_{0}})}}{{{{\hbar }^{2}}}}} ,$ ${{E}_{1}} = {{\left( {\frac{{\alpha \pi }}{{180}}} \right)}^{2}}E$ – нормальная составляющая энергии падающих электронов E, α – угол скольжения пучка в градусах, r – амплитуда отраженной волны, t – амплитуда прошедшей волны, V₀ > 0 – высота потенциальной ступеньки.

Сшивание волновых функций свободных электронов с блоховскими волнами было проведено в [29] с использованием матрицы рассеяния. В настоящей работе сшивание функций и решение полученных систем уравнений относительно t было проведено непосредственно. В результате получено компактное аналитическое выражение для коэффициента прохождения T:

где модуль блоховского волнового вектора μ определяется из уравнения дисперсии

Отсюда, соответственно, находится коэффициент отражения $R = 1 - T.$

Ниже приведена графическая иллюстрация расчетов по этой формуле для различных значений параметров модели.

РАСЧЕТЫ, ГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

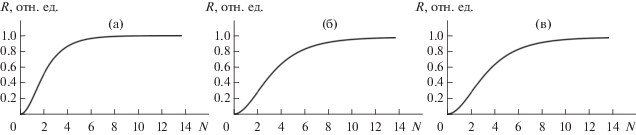
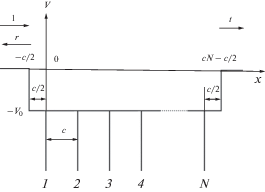
Прежде необходимо в формуле (2) выбрать значения входящих в нее параметров, а также график зависимости R(α) при этих значениях, который поможет интерпретировать расчеты. Был выбран рис. 4 из [22], который приведем в настоящей работе и обозначим как рис. 3. Таким образом, во всех нижеприводимых графиках при расчетах были выбраны следующие значения параметров: V₀ = 10 эВ, E = 10 кэВ, y = c ²U/2π = –1. На рис. 3 ясно видны границы зон решетки.

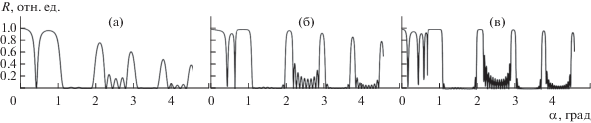
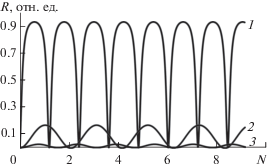
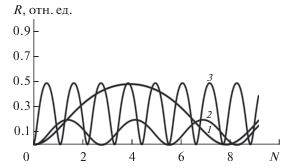
На рис. 4 приведены результаты вычисления коэффициента отражения R_α(N) при трех различных значениях угла скольжения α. Угол α = 0.5° соответствует первой видимой разрешенной зоне (рис. 3), α = 1.4° – второй разрешенной зоне, а α = 2.5° – третьей. Видим, что период осцилляций во всех трех случаях различный и всегда больше единицы. Из формулы (2) следует, что он равен единице тогда, когда μ = π/c, т.е. на одной из двух границ каждой разрешенной зоны. Также отмечаем, что значения амплитуды зависят от величины α. На рис. 4 они определяются значениями огибающей осцилляций между основными рефлексами на рис. 3 при соответствующих углах α.

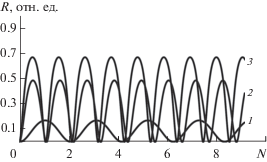
На рис. 5 изображены графики R_α(N) при трех значениях угла скольжения α, лежащих в одной, а именно в третьей, разрешенной зоне (рис. 3). Видна зависимость амплитуды и периода осцилляций от α.

На рис. 6 эта закономерность особенно отчетливо проявляется. Вблизи левого края второй разрешенной зоны (рис. 3) при α = 1.1° период почти равен единице. В средней части зоны (α = = 1.4°) – почти двум. А вблизи правой границы – почти 15. Эти закономерности следуют и из теоретического анализа дисперсионной зависимости для электрона в одномерной решетке E(μ). В следующей разрешенной зоне (в третьей на рис. 3) период наоборот убывает при росте α (рис. 7). У левой границе зоны (α = 2.2°) он равен приблизительно восьми. Для α = 2.4° он составляет ΔN = 2.4. А у правой границе третьей зоны при α = 2.85°, ΔN $ \sim 1.$ В четвертой разрешенной зоне эта закономерность меняется на обратную и повторяет закономерность второй зоны. Эти свойства вытекают и из анализа зависимости E(μ) в схеме приведенных зон.

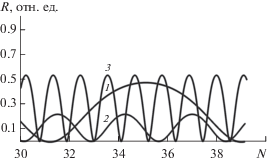
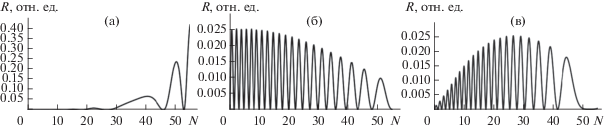
Рис. 8 иллюстрирует эксперимент, когда в процессе роста толщина монокристаллической пленки увеличивается от нуля до N = 55 монослоев, равномерно изменяется угол скольжения в трех диапазонах значений α. На рис. 7а – в диапазоне от 1.77° до 1.97°, т.е. на правом участке второй разрешенной зоны (рис. 3). На рис. 7б диапазон углов α изменяется в средней части второй разрешенной зоны. А в случае рис. 7в – в левой части. Во всех трех случаях видим, что с равномерным изменением толщины пленки N и равномерным изменением α изменяются амплитуда и период осцилляций.

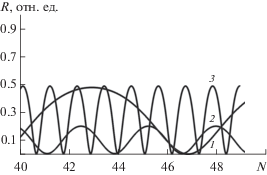
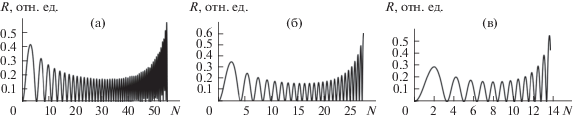
Экспериментальная ситуация, когда угол наклона образца α по отношению к пучку электронов плавно изменяется от 2.18° до 2.86° (третья разрешенная зона) при одновременном равномерном росте монокристаллической пленки в трех диапазонах толщин, приведена на рис. 9. И здесь наблюдается характерное непрерывное изменение периодов и амплитуд осцилляций.

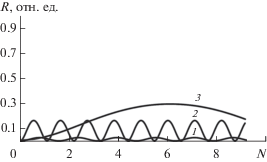
На рис. 10 приведены результаты расчета R_α(N) для трех случаев, когда зеркальный рефлекс лежит в диапазонах угла α, соответствующих трем последовательным брэгговским рефлексам. Угол α = 0.9° лежит в диапазоне первого рефлекса (в первой запрещенной зоне) (рис. 3), угол α = 2.1° соответствует второй запрещенной зоне, и угол α = 2.95° – третьей запрещенной зоне. При этих углах толщина пленки каждый раз изменяется от нуля до 13 монослоев. Видим, что в этом случае осцилляции не наблюдаются, что и понятно – нет условий для возникновения квантового размерного эффекта, поскольку указанные значения углов соответствуют запрещенным зонам в кристалле, и значение μ становится мнимым. Этот результат следует учитывать при экспериментальном наблюдении эффекта. Необходимо так сориентировать пленку, чтобы зеркальный рефлекс не совпадал ни с одним брэгговским рефлексом.

Здесь нужно добавить следующие рассуждения. Приведенные формулы (1), (2), которые применяются для иллюстрации предлагаемых экспериментов, были выведены для зеркального рефлекса, поскольку использовалась одномерная модель кристалла. Для описания дифракции нужна, по крайней мере, двумерная модель. Однако и на основе одномерной модели можно высказать некоторые соображения относительно дифракционной картины. В частности, следующие. Закон формирования двумерной картины дифракции от N параллельных кристаллических плоскостей аналогичен закону R(α), полученному для одномерной решетки (формулы (1), (2)). Поэтому можно выдвинуть следующую гипотезу. Интенсивность суммарной дифракционной картины или любой точки на ней будет зависеть от угла скольжения и становиться максимальной при тех углах α, которые совпадают с брэгговскими рефлексами. Это следует из закона изменения интенсивности зеркального рефлекса (например, рис. 3). Здесь, однако, следует заметить, что пики между брэгговскими рефлексами (рис. 3) в случае гомоэпитаксиальной пленки не будут наблюдаться. Поэтому не будет и соответствующих им изменений интенсивности дифракционной картины.

Эту гипотезу легко проверить экспериментально. Нужно, варьируя угол скольжения α, наблюдать за изменением интенсивности дифракционной картины. Если интенсивность становится максимальной при тех углах α, при которых зеркальный рефлекс совпадает с одним из брэгговских, то гипотеза верна. Следовательно, можно косвенно судить об ориентации зеркального рефлекса, даже если по какой-то причине его не видно на дифракционной картине. Как следует из рис. 10, при углах α, совпадающих с брэгговскими, при которых интенсивность дифракционных рефлексов максимальна, осцилляции при росте пленки не должны наблюдаться. Однако для их выявления можно рекомендовать следующие действия. Нужно, вращая образец, “попасть” в один из максимумов, а затем сместиться из него на угол, при котором интенсивность дифракционной картины заметно упадет. Это соответствует диапазону углов, в котором возникает квантовый размерный эффект, и, следовательно, могут наблюдаться длинноволновые осцилляции интенсивности отраженного пучка при росте пленки.

Начальные фазы осцилляций определяются как значениями N, так и значениями α. Рис. 11 и 12 иллюстрируют зависимость фаз осцилляций от толщины пленки N и от угла α. На рис. 11 начальные фазы для N = 30 определяются углом α. А на рис. 12 начальные фазы при тех же трех значениях α, что и на рис. 11, но при значении N = 40 будут другими. То есть в этом случае они определяются величиной N. Для коротковолновых осцилляций проблема определения фаз колебаний является довольно сложной задачей [18, 19]. Здесь же получаем простые зависимости (2), которые иллюстрируют рис. 11 и 12.

ЗАКЛЮЧЕНИЕ

В настоящей работе рассмотрен процесс взаимодействия пучка электронов с растущей гетероэпитаксиальной пленкой. Угол скольжения пучка такой же, как в стандартной схеме дифракции быстрых электронов. Рассчитаны и приведены кривые R_α(N) для различных экспериментальных ситуаций. В качестве исходных формул выбраны выражения, полученные ранее [22]. Показана возможность возникновения длинноволновых осцилляций интенсивности зеркального отражения от растущей гетероэпитаксиальной пленки с периодом от единицы до бесконечности. Обоснован механизм их возникновения. Он обусловлен квантовым размерным эффектом. Предложены различные экспериментальные способы их наблюдения. Выдвинута гипотеза, объясняющая такое поведение R_α(N) не только для зеркального рефлекса, но и для любого фрагмента дифракционной картины. На основе этой гипотезы предлагается методика выбора угла скольжения α, необходимого для регистрации осцилляций. Предположено, что полученные в этих условиях длинноволновые осцилляции будут модулировать коротковолновые колебания. Этот эффект экспериментально наблюдался при эпитаксии Ni на W (соответствующие кривые приведены на рис. 6 и 7 в [25]). Однако на приведенных в работе графиках виден экспоненциальный спад интенсивности осцилляций, который, вероятно, обусловлен поглощением электронов пленкой. В обсуждаемой модели этот эффект не учитывался, поэтому он и не выявляется на графиках. Здесь же отметим последние достижения в создании атомарно гладких террас роста пленок большой площади [30–34]. Такие образцы особенно подходят для наблюдения квантового размерного эффекта, предложенного в [22], а также в настоящей работе.