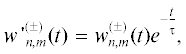Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 2, стр. 16-21
Моделирование эволюции функций распределения кластеров по размерам в полярных растворах фуллерена С60
Т. В. Тропин 1, *, М. В. Авдеев 1, В. Л. Аксенов 1, 2
1 Лаборатория нейтронной физики им. И.М. Франка,
Объединенный институт ядерных исследований
Дубна, Россия
2 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: ttv@jinr.ru
Поступила в редакцию 15.01.2018
После доработки 15.01.2018
Принята к публикации 15.01.2018
Аннотация
Предложен метод расчета эволюции функций распределения кластеров фуллерена С60 по размерам в полярном растворителе в рамках предложенной ранее модели ограниченного роста. Данный метод позволяет рассчитать функцию распределения f(r, t) в произвольный момент времени для любых заданных параметров системы. В качестве примера рассчитаны эволюция среднего размера кластеров, концентрации мономеров и функции f(r, t) для раствора фуллерена в модельном полярном растворе, получены спектры малоуглового рассеяния нейтронов в разные моменты времени с начала агрегации в растворе.
ВВЕДЕНИЕ
Открытие в конце прошлого века фуллеренов, новой аллотропной формы углерода, можно считать одним из важнейших открытий в области физики наносистем [1]. Интерес к исследованию этих углеродных наночастиц поддерживается как открытием новых форм углерода (углеродные нанотрубки и графен), так и перспективами их практических применений. Отчасти эти перспективы связаны с тем, что фуллерены С60, С70 сравнительно хорошо растворяются в широком классе органических и неорганических растворителей [2]. В некоторых растворах фуллерены проявляют ряд интересных свойств, например сольватохромизм и образование, и рост кластеров. В результате экспериментальных исследований этих явлений предложена классификация растворов фуллерена по типу кластерообразования [3]. С точки зрения наблюдаемых кинетических явлений наиболее интересным является второй класс растворов – растворы фуллеренов в полярных растворителях, таких как N-метилпирролидон (NМП) [4] и пиридин [5]. Исследование и описание кинетики образования и роста кластеров в этих системах важно с точки зрения практических биомедицинских применений, а также является интересной задачей для применения теории кластерообразования. При моделировании процесса роста кластеров в этих растворах необходимо учитывать влияние образования комплексов фуллерен–растворитель на агрегацию С60.
В работах [6–8] предложены модели для описания кинетики агрегации фуллерена в полярных растворителях. В частности, из сравнения двух моделей, по-разному учитывающих влияние комплексообразования на рост кластеров, показано, что модель ограниченного роста может использоваться для описания экспериментальных данных для раствора С60 в NМП [9]. Однако численные расчеты полной временнóй эволюции функции распределения кластеров f(r, t) по размерам в растворе невозможны с точки зрения любых современных вычислительных мощностей – требуется решение ~108 кинетических уравнений на большом интервале времени. Поэтому в [7, 9] оценка функций f(r, t) выполнялась методом численной экстраполяции расчетных данных. Этот метод позволяет получить искомые функции, однако может вносить ошибку, поскольку функция для экстраполяции выбиралась произвольно, закон экстраполяции не был известен. Кроме того, сама функция экстраполяции меняется при изменении любых параметров системы.
В настоящей работе предложен метод расчета эволюции функций распределения кластеров фуллерена С60 по размерам в полярном растворителе, в котором устранены указанные недостатки. Предложен метод масштабирования временнóй шкалы, приводящий зависимость среднего размера частиц от времени к типичному “закону t1/3”, полученному Слезовым [10]. При этом показано, что функции распределения точно описываются с помощью аналитических выражений, полученных в [10]. Таким образом, для расчета полной эволюции кластерного состояния в растворе необходимо численно рассчитать f(r, t) до стадии созревания Оствальда, после чего воспользоваться полученными оценками. В качестве примера применения предложенного метода рассчитаны функции распределения и кривые малоуглового рассеяния нейтронов (МУРН) для модельного раствора С60, близкого по параметрам к раствору С60/NМП.
МОДЕЛЬ ОГРАНИЧЕННОГО РОСТА КЛАСТЕРОВ
Модель ограниченного роста кластеров для растворов фуллерена предложена в [3, 7, 8]. В качестве базового подхода используется метод кинетических уравнений для сегрегации в однокомпонентной системе [11]. Уравнения описывают временнýю эволюцию функции распределения кластеров по размерам f(n, t):
(1)
$\begin{gathered} \frac{{\partial f(n,t)}}{{\partial t}} = w_{{n - 1,n}}^{{( + )}}f(n - 1,t) - w_{{n,n - 1}}^{{( - )}}f(n,t) + \\ + \,\,w_{{n + 1,n}}^{{( - )}}f(n + 1,t) - w_{{n,n + 1}}^{{( + )}}f(n,t), \\ \end{gathered} $(2)
$\Delta G(n) = - n\Delta {\mu } + {{\alpha }_{2}}{{n}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},\,\,\,\,{{\alpha }_{2}} = 4\pi \sigma r_{0}^{2},$(3)
$w_{{n,n + 1}}^{{( + )}}(t) = 4\pi Dc(t){{r}_{0}}{{n}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$Сформулированная таким образом кинетическая теория описывает нуклеацию и рост кластеров для большого числа различных систем [12]. Для описания кинетики агрегации в полярных растворах фуллеренов необходимо рассмотреть модифицированную модель, в которой учитывается влияние образования комплексов фуллерен–растворитель на рост кластеров. Согласно [6–8] ограничение процессов роста и распада кластеров, обусловленное комплексообразованием, можно качественно учесть, если изменить вероятности w(+) и w(–) по формуле
где τ – параметр модели, отвечающий характерному времени образования комплексов в растворе.Уравнения (1) решаются для приведенной шкалы времени, где коэффициент масштабирования равен 4πDceqr0. Далее в большинстве случаев под t подразумевается данное безразмерное время, для избегания недоразумений будут указываться единицы.
Как отмечено во введении, получить полную эволюцию f(n, t) с помощью численных расчетов невозможно, поэтому в настоящей работе предложен метод, опирающийся на аналитический расчет асимптотики поздних стадий роста кластеров, развитый Слезовым, Лифшицем и Сагаловичем [10]. Для применения этого метода показано, что функции распределения соответствуют функциям Слезова, а эволюция среднего размера кластеров может быть сведена к закону t1/3 путем преобразования шкалы времени. Это позволяет для любого τ получить функции f(r, t) для любого значения t. В качестве примера применения данного метода выполнены расчеты эволюции кластерного состояния фуллеренов С60 в полярном растворе.
МОДЕЛИРОВАНИЕ КИНЕТИКИ АГРЕГАЦИИ С60
Для моделирования агрегации фуллерена в определенном растворителе необходимо задать следующие параметры системы: энергию поверхностного натяжения σ, степень пересыщения начального раствора c(t = 0)/ceq, коэффициент диффузии С60 в жидкости D, а также время образования комплекса фуллерен–растворитель τ. Для таких полярных растворителей, как пиридин или NМП, значения первых трех параметров модели неизвестны, поэтому будем рассматривать некоторый “модельный” растворитель фуллерена, для которого σ оценивается из расчетов энтальпии растворения С60 в бензоле (α2/kBT = 8), коэффициент диффузии также взят для бензола D = 9.1 × × 10–10 м2/с, равновесная концентрация оценена как 1/10 от максимальной концентрации раствора в NМП: сeq = 7.525 × 1022 м–3. Характерное время комплексообразования С60–NМП измерялось в [13]: τ ~ 2 × 103 с. Радиус молекулы С60 в растворе равен 0.5 нм. В результате можно оценить коэффициент перехода от приведенного времени к реальному: 4πDceqr0 ≈ 4.3 × 105. Таким образом, τ ≈ ≈ 8.6 × 108. Необходимо получить функции распределения кластеров по радиусам f(r, t) для данного τ. Для этого выполнялись последовательные расчеты f(n, t) для следующего набора значений τ: 104, 5 × 104, 105, 3 × 105, 5 × 105. Данного набора достаточно для выполнения полной оценки эволюции функций f(r, t).
Анализ хода эволюции кластерного состояния в растворе начнем с временнóй зависимости среднего радиуса частиц:
(5)
$\left\langle r \right\rangle = \frac{{\sum\limits_{n = {{n}_{{\min }}}}^{{{n}_{{\max }}}} {f(n,t){{r}_{0}}{{{\left( {n\gamma } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} }}{{\sum\limits_{n = {{n}_{{\min }}}}^{{{n}_{{\max }}}} {f(n,t)n} }},$Рис. 1.
Зависимость среднего радиуса частиц в модельном растворе от времени для разных значений параметра модели τ (жирные кривые), и для случая приведенной шкалы времени t ′ (пунктирная кривая, см. формулу (7)). Римскими цифрами обозначены разные стадии эволюции системы [10,11]. Значения τ = 104, 5 × 104, 105, 3 × 105, 5 × 105 последовательно изменяются от нижней сплошной кривой вверх.
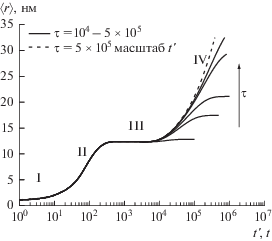
Как видно, зависимость 〈r〉 определяется значением τ: на временах t, превышающих τ в два–три раза, достигается стабильное значение размера частиц (и функции распределения кластеров) в растворе. В целом рост кластеров проходит в четыре стадии, последней является стадия созревания Оствальда, на которой имеет место устойчивый рост крупных агрегатов [11]. В [10] показано, что для агрегации, ограниченной диффузией, на этой стадии выполняется так называемый “закон t1/3”:
(6)
${{\bar {R}}^{3}} = \bar {R}_{0}^{3} + \frac{4}{9}D\alpha t,\,\,\,\,\bar {R} \gg {{\bar {R}}_{0}},$(7)
${{t}^{\prime }} = \tau \left( {1 - {{e}^{{ - {t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-0em} \tau }}}}} \right).$В терминах t′ все кривые 〈r〉, независимо от значения τ, совпадают. Более того, для достаточно большого значения времени t' будет выполняться закон (6). Таким образом, если взять начальные стадии роста кластеров I–III, а также переходную стадию между III и IV (из численных расчетов), и далее добавить выражение вида (6), можно получить полную зависимость 〈r〉 от t'. Для заданного τ обратное преобразование к шкале времени t выполняется по формуле
(8)
$t = - \tau \ln \left( {1 - \frac{{{{t}^{\prime }}}}{\tau }} \right),\,\,\,\,{{t}^{\prime }} < \tau .$Аналогичным образом можно выполнить расчеты для зависимости числа мономеров в растворе, для которых также выполняется аналог “закона t1/3”. Концентрация мономеров в системе требуется для расчета экспоненциально затухающей функции распределения малых кластеров по размерам (для n < nmin). На рис. 2 представлены полученные описанным методом зависимости 〈r〉 и c(t) для τ = 5 × 108, что примерно соответствует 2 × × 103 с – времени образования комплексов фуллерен–NМП в растворе С60/NМП [13]. Также на рис. 2 штрихпунктирной линией представлена общая зависимость 〈r〉 от t' до применения формулы (8).
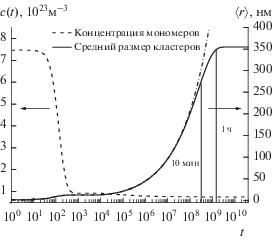
Рис. 2.
Временнáя эволюция среднего радиуса кластеров и концентрации мономеров в растворе, выполненная с помощью нового предложенного метода расчетов. Значение параметра τ = 5 × 108 соответствует экспериментально определенному времени комплексообразования в растворе С60/NМП.
Поскольку после преобразования шкалы времени зависимость основных параметров модельной системы совпала с асимптотическими расчетами для обычной агрегации, можно ожидать, что и функции распределения кластеров по размерам совпадут с функцией, предложенной в [10]:
(9)
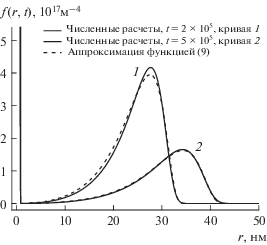
$\begin{gathered} f(R,t) = n(t)P\left( {\frac{R}{{\bar {R}}}} \right)\frac{1}{{\bar {R}}}, \\ P(u) = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{3}^{4}}e}}{{{{2}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}}}\frac{{{{u}^{2}}\exp \left( { - \frac{1}{{1 - \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}} \right)u}}} \right)}}{{{{{\left( {u + 3} \right)}}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}}{{{\left( {\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right) - u} \right)}}^{{{{11} \mathord{\left/ {\vphantom {{11} 3}} \right. \kern-0em} 3}}}}}},\,\,\,\,0 < u < {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \\ {0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,u \geqslant {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},} \end{array}} \right. \\ \end{gathered} $Рис. 3.
Функции распределения кластеров по радиусам f(r, t), полученные из численных расчетов для τ = = 5 × 105, при t = 2 × 105, t = 5 × 105 (жирные кривые) и их аппроксимация асимптотической функцией распределения (9) (пунктирные кривые).
Таким образом, пользуясь зависимостью, представленной на рис. 2, можно получить функцию распределения кластеров по размерам f(r, t) для любого значения времени t: при t < t0 необходимо пользоваться результатами численных расчетов, а при t > t0 – аналитическими выражениями. Значение t0, зависящее от параметров расчетов, в настоящей работе выбрано как t0 = 3 × 105. На рис. 4 представлены расчетные функции распределения кластеров по радиусам в системе.
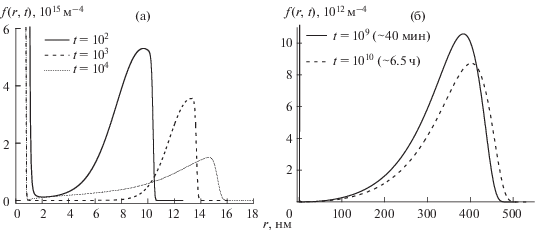
Рис. 4.
Рассчитанные функции распределения кластеров С60 по размерам в модельном полярном растворе. а – начальные стадии роста кластеров (время менее 1 с); б – рост крупных кластеров, время эволюции системы указано на рисунке.
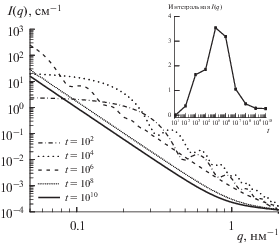
С помощью предложенного метода расчетов и полученных функций распределения f(r, t) можно выполнять оценку данных для разных экспериментальных методов. В [9] предложен метод вычисления спектров МУРН для растворов фуллерена. Интенсивность рассеянных нейтронов в рамках приближения, рассматривающего кластеры фуллерена как однородные шары, вычисляется по формуле
(10)
$I(q) = \int\limits_0^{{{R}_{{\max }}}} {{{{\left( {\rho (R) - {{\rho }_{{NMP}}}} \right)}}^{2}}} {{V}^{2}}(R){{I}_{0}}(qR)f(R)dR,$ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Полученные в предыдущем разделе функции распределения, данные об эволюции среднего радиуса частиц и данные МУРН можно сравнить с опубликованными экспериментальными результатами для раствора С60/NМП. Так, в [14] методом динамического светорассеяния наблюдался достаточно быстрый рост агрегатов С60 в смесях NМП/толуол. Максимальный размер агрегатов, порядка 60 нм, достигался за первый час экспериментов. По другим сведениям размер агрегатов в чистом NМП составляет более 200 нм при аналогичной по скорости кинетике роста. Такие же по порядку и значения скорости растворения и комплексообразования в этом растворе [13] (по данным спектрофотометрии). С другой стороны, есть результаты, указывающие на более медленную кинетику – уменьшение концентрации мономеров в указанных системах [4] протекает в течении нескольких суток. В целом можно заключить, что в настоящее время недостаточно сведений о кинетике роста кластеров фуллерена в чистом NМП, пиридине или другом полярном растворителе. Данные спектрофотометрии должны быть дополнены, например, данными динамического светорассеяния и МУРН, что позволит качественно сравнить теоретические расчеты с экспериментом. Когда будет получена новая информация, по закону роста среднего размера кластеров можно будет также заключить о механизме их роста.
Отметим, что в настоящей работе расчеты выполнены для “модельного” раствора, который отличается от раствора в NМП. Причиной отличий от реальной системы могут стать другая степень пересыщения и другие значения коэффициента диффузии D и поверхностной энергии σ. Необходимо определить данные параметры системы для дальнейших расчетов.
Другим направлением исследований должно стать моделирование разбавления раствора жидкостями разной полярности в различных пропорциях. В [15] обнаружен и исследован эффект критического разрушения кластеров при добавлении в систему воды объемной долей более 40%. Серия аналогичных исследований была впоследствии выполнена для случая разбавления слабополярным растворителем – толуолом [16]. Очевидно, что результаты настоящей работы позволяют выполнить моделирование разбавления, распространяя результаты на реальные системы.
ЗАКЛЮЧЕНИЕ
Предложен метод расчета полной эволюции функций распределения по размерам кластеров С60 в полярном растворе. Рассмотрена модельная система, по некоторым параметрам соответствующая раствору фуллерена в NМП. Получена эволюция среднего радиуса кластеров и функций f(r, t), а также выполнен расчет спектров МУРН для данной системы.
Численные расчеты функций распределения кластеров по размерам выполнены на гетерогенном вычислительном кластере HybriLIT, Лаборатория информационных технологий, ОИЯИ (hybrilit.jinr.ru).
Список литературы
Kroto H.W., Heath J.R., O’Brien S.C. et al. // Nature. 1985. V. 318. P. 162.
Ruoff R.S., Tse D.S., Malhotra R. et al. // J. Phys. Chem. 1993. V. 97. P. 3379.
Авдеев М.В., Аксенов В.Л., Тропин Т.В. // ЖФХ. 2010. Т. 84. № 8. С. 1405.
Kyzyma O.A., Korobov M.V., Avdeev M.V. et al. // Chem. Phys. Lett. 2010. V. 493. P. 103.
Mrzel A., Mertelj A., Omerzu A. et al. // J. Phys. Chem. B. 1999. V. 103. P. 11256.
Tropin T.V., Avdeev M.V., Kyzyma O.A., Aksenov V.L. // Phys. Status Solidi. B. 2010. V. 247. P. 3022.
Tropin T.V., Avdeev M.V., Kyzyma O.A. et al. // Phys. Status Solidi. B. 2011. V. 248. P. 2728.
Tropin T.V., Jargalan N., Avdeev M.V. et al. // J. Mol. Liq. 2012. V. 175. P. 4.
Тропин Т.В., Jargalan N., Авдеев М.В. и др. // ФТТ. 2014. Т. 56. Вып. 1. С. 147.
Слезов В.В., Сагалович В.В. // Успехи физ. наук. 1987. Т. 151. Вып. 1. С. 67.
Schmelzer J.W.P. // Mater. Phys. Mech. 2003. V. 6. P. 21.
Slezov V.V. Kinetics of First-Order Phase Transitions. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2009. 415 p.
Jargalan N., Tropin T.V., Avdeev M.V. et al. // Nanosyst. Physics Chem. Math. 2016. V. 7. P. 99.
Alfè M., Apicella B., Barbella R. et al. // Chem. Phys. Lett. 2005. V. 405. P. 193.
Aksenov V.L., Avdeev M.V., Tropin T.V. et al. // Phys. B. Condens. Matter. 2006. V. 385–386. P. 795.
Kyzyma O.A., Kyrey T.O., Avdeev M.V. et al. // Chem. Phys. Lett. 2013. V. 556. V. 178.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования