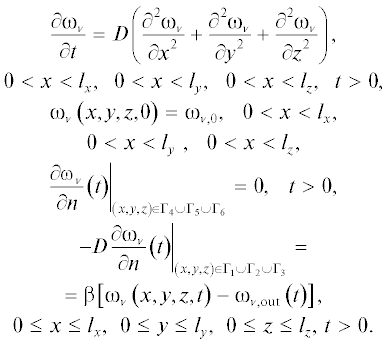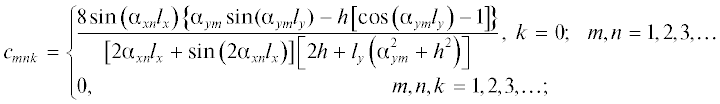Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 3, стр. 90-96
Макроскопическое и микроскопическое моделирование процессов взаимодействия водяного пара и пор пластинчатого типа
Э. Г. Никонов 1, *, M. Pavluš 2, M. Popovičová 2
1 Объединенный институт ядерных исследований
141980 Дубна, Россия
2 University of Prešov
08001 Prešov, Slovakia
* E-mail: e.nikonov@jinr.ru
Поступила в редакцию 20.03.2018
После доработки 17.07.2018
Принята к публикации 17.07.2018
Аннотация
Одной из разновидностей пор, часто встречающихся в натуральных или искусственных конструкционных материалах, являются так называемые пластинчатые поры. Сложность исследования процессов взаимодействия газообразного вещества, в частности, водяного пара и пластинчатой поры связана со сложным рельефом стенок поры и неравномерным распределением значений основных термодинамических характеристик водяного пара по протяженности поры. В связи с этим в работе сформулирован комбинированный подход к описанию процессов взаимодействия поры и водяного пара. Данный подход основан на совместном использовании макроскопической диффузионной и молекулярно-динамической модели. С учетом сложности геометрии стенок поры уравнения макроскопической диффузионной модели могут быть решены численно, для этого используется таблица пространственного распределения значений коэффициента диффузии, полученного с использованием молекулярно-динамического моделирования. Данный подход позволит получить более точное решение уравнений макроскопической диффузионной модели, и, соответственно, повысить точность моделирования процессов взаимодействия поры и водяного пара.
ВВЕДЕНИЕ
Экспериментальные и теоретические исследования процессов взаимодействия воды и водяного пара с пористыми материалами представляют значительный интерес для различных сфер человеческой деятельности, включая строительство, защиту окружающей среды и нанотехнологии. Характеристики взаимодействия воды и пористых материалов зависят не только от свойств воды и водяных растворов в жидкой и газообразной фазе, но и от пористой структуры конкретного материала, геометрии, других свойств и характеристик взаимодействия с водой индивидуальных пор.
Пористые материалы натуральные или искусственные, органические или неорганические, в зависимости от структуры пористости могут быть разделены на следующие типы:
1) Материалы с порами разного размера от нанометра до миллиметра.
2) Материалы с регулярной и нерегулярной структурой пор.
3) Различные композитные материалы (металлы, оксиды).
4) Материалы, различающиеся способом изготовления.
Индивидуальные поры различаются по следующим основным параметрам: доступность и форма. Относительно доступности поры могут быть закрытые, открытые, слепые поры (тупиковые и мешкообразные) и сквозные. Относительно формы поры могут быть следующих типов: цилиндрические открытые, цилиндрические слепые, формы чернильницы, воронкообразные и шероховатые поры [1].
Кроме того, в соответствии с The International Union of Pure and Applied Chemistry (IUPAC) классификацией поры характеризуются по своим размерам [2].
1) Микропоры (меньше 2 нм): больше, чем типичная средняя длина свободного пробега типичного флюида.
2) Мезопоры (между 2 и 50 нм): такого же или меньше размера, чем средняя длина свободного пробега.
3) Макропоры (больше 50 нм): размер поры сравним с размерами молекул.
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ МОДЕЛИРОВАНИЯ
В данной работе для моделирования взаимодействия водяного пара и пластинчатой поры предлагается подход, состоящий из двух этапов. На первом этапе методом молекулярной динамики [3] получается пространственное распределение коэффициента диффузии. На втором этапе решается макроскопическое уравнение диффузии [4] для получения пространственного распределения концентрации водяного пара для каждого момента времени с использованием полученного на предыдущем этапе пространственного распределения коэффициента диффузии для данного момента времени. В работе проведен сравнительный анализ распределений коэффициента диффузии для процессов высыхания и намокания пластинчатой поры при взаимодействии с водяным паром с использованием моделирования на основе непрерывного уравнения диффузии и моделирования методом молекулярной динамики. Для сравнительных расчетов использовалась прямоугольная геометрическая модель пластинчатой поры.
МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ ВОДЯНОГО ПАРА С ПЛАСТИНЧАТОЙ ПОРОЙ С ИСПОЛЬЗОВАНИЕМ НЕПРЕРЫВНОГО УРАВНЕНИЯ ДИФФУЗИИ
В соответствии с макроскопической диффузионной моделью динамика водяного пара в поре
может быть описана в терминах концентрации водяного пара 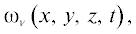 заданной в каждой точке пространства $\left( {x,y,z} \right)$ в момент времени $t\quad$ при помощи непрерывного уравнения диффузии:
заданной в каждой точке пространства $\left( {x,y,z} \right)$ в момент времени $t\quad$ при помощи непрерывного уравнения диффузии:
Здесь 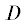 – диффузионный коэффициент [нм2/пс], ${{l}_{x}},\,\,{{l}_{y}},\,\,{{l}_{z}}$ – размеры поры в нм, ${{{\omega }}_{{\text{v},\quad0}}}$ – начальная концентрация водяного пара, Γi$(i = 1--6)$ – границы поры, ${\beta }$ – коэффициент переноса водяного пара из поры во внешнюю область [нм2/псек], ${{{\omega }}_{{\text{v},{\text{out}}}}}\left( t \right)$ – концентрация водяного пара вне поры [нг/нм3].
– диффузионный коэффициент [нм2/пс], ${{l}_{x}},\,\,{{l}_{y}},\,\,{{l}_{z}}$ – размеры поры в нм, ${{{\omega }}_{{\text{v},\quad0}}}$ – начальная концентрация водяного пара, Γi$(i = 1--6)$ – границы поры, ${\beta }$ – коэффициент переноса водяного пара из поры во внешнюю область [нм2/псек], ${{{\omega }}_{{\text{v},{\text{out}}}}}\left( t \right)$ – концентрация водяного пара вне поры [нг/нм3].
Кроме того, предполагается, что в начале процесса диффузии начальные условия определяются начальным распределением концентрации водяного пара ${{{\omega }}_{{\text{v},0}}}.$ Границы поры $({{{\Gamma }}_{4}},{{{\Gamma }}_{5}},\quad{{{\Gamma }}_{6}})$ непроницаемы для водяного пара, т.е. молекулы воды отражаются от данных границ, обмена между порой и внешней средой не происходит. Границы ${{{\Gamma }}_{1}},\quad{{{\Gamma }}_{2}},\quad{{{\Gamma }}_{3}}$ являются прозрачными для молекул воды, т.е. через эти границы может происходить обмен молекулами воды между внутренним объемом поры и внешней средой. Мы предполагаем, что концентрация водяного пара во внешней среде может быть выражена через относительную влажность ${{{\varphi }}_{0}}\left( {0 \leqslant {{{\varphi }}_{{0{\;}}}} \leqslant 1} \right)$ следующим образом:
Линейная задача (1) в случае прямоугольной области может быть решена методом разделения переменных [1]:
(2)
$\begin{gathered} {{{\omega }}_{\text{v}}}\left( {x,y,z,t} \right) = {{{\varphi }}_{0}}\quad{{{\omega }}_{{s\text{v}}}}\left( {{{T}_{0}}} \right) + \\ + \,\,\left[ {{{{\omega }}_{{\text{v},0}}} - {{{\varphi }}_{0}}{{{\omega }}_{{s\text{v}}}}\left( {{{T}_{0}}} \right)} \right]\mathop \sum \limits_{k = 0}^\infty \mathop \sum \limits_{m = 1}^\infty \mathop \sum \limits_{n = 1}^\infty {{e}^{{D{{{\lambda }}_{{mnk}}}t}}}{{c}_{{mnk}}} \times \\ \times \,\,\cos \left( {{{{\alpha }}_{{xn}}}x} \right)\left[ {\cos \left( {{{{\alpha }}_{{ym}}}y} \right) + \frac{h}{{{{{\alpha }}_{{ym}}}}}\sin \left( {{{{\alpha }}_{{ym}}}y} \right)} \right]\cos \left( {{{{\alpha }}_{{zk}}}z} \right), \\ h = \frac{{\beta }}{D},\,\,\,0 \leqslant x \leqslant {{l}_{x}},\,\,\,\,0 \leqslant y \leqslant {{l}_{y}},\,\,\,\,0 \leqslant z \leqslant {{l}_{z}},\,\,\,\,t > 0. \\ \end{gathered} $Здесь ${{c}_{{mnk}}}$ – коэффициенты разложения единицы:
${{{\lambda }}_{{mnk}}}$ – собственные значенияМОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ ВОДЯНОГО ПАРА С ПЛАСТИНЧАТОЙ ПОРОЙ МЕТОДОМ МОЛЕКУЛЯРНОЙ ДИНАМИКИ
В основе методов классической молекулярной динамики лежит модельное представление о многочастичной системе, в которой все частицы (атомы или молекулы) представляют собой материальные точки. Поведение отдельной частицы описывается классическими уравнениями движения Ньютона, которые могут быть записаны в следующем виде
Здесь $i$ – номер частицы $\left( {1 \leqslant i{\;} \leqslant N} \right),$ $N{\;}$ – полное число частиц, ${{m}_{i}}$ – масса частицы, ${{{\mathbf{f}}}_{i}}$ – равнодействующая всех сил, действующих на частицу, имеющая следующее представление.
(4)
${{{\mathbf{f}}}_{i}} = {\;}\frac{{\partial U\left( {{{{\mathbf{r}}}_{1}},{\;} \ldots ,{\;}{{{\mathbf{r}}}_{N}}} \right)}}{{\partial {{{\mathbf{r}}}_{i}}}} + {\;}{\mathbf{f}}_{i}^{{ex}},$В данной работе для моделирования процессов взаимодействия водяного пара и пластинчатой поры использовался потенциал Леннарда–Джонса [5]. Выбор потенциала обусловлен короткодействующим характером взаимодействия молекул водяного пара. Потенциал Леннарда–Джонса записывается в следующем виде:
(5)
$U\left( r \right) = 4{\varepsilon }\left[ {{{{\left( {\frac{{\sigma }}{r}} \right)}}^{{12}}} - {{{\left( {\frac{{\sigma }}{r}} \right)}}^{6}}} \right]\quad,$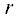 – расстояние между центрами частиц, $\quad{\varepsilon }$ – глубина потенциальной ямы, ${\sigma }$ – расстояние, на котором энергия взаимодействия становится равной нулю. Параметры
${\varepsilon }$ и ${\sigma }$ являются характеристиками атомов соответствующего вещества. Минимум потенциала находится
в точке ${{r}_{{{\text{min}}}}} = {\sigma }\sqrt[6]{2}.$
– расстояние между центрами частиц, $\quad{\varepsilon }$ – глубина потенциальной ямы, ${\sigma }$ – расстояние, на котором энергия взаимодействия становится равной нулю. Параметры
${\varepsilon }$ и ${\sigma }$ являются характеристиками атомов соответствующего вещества. Минимум потенциала находится
в точке ${{r}_{{{\text{min}}}}} = {\sigma }\sqrt[6]{2}.$
При больших $r$ молекулы притягиваются, что соответствует члену $ - \quad{{\left( {\frac{{\sigma }}{r}} \right)}^{6}}$ в формуле (3). Эту зависимость можно обосновать теоретически, и обусловлена она силами Ван-дер-Ваальса (диполь-дипольное индуцированное взаимодействие). На малых же расстояниях молекулы отталкиваются из-за обменного взаимодействия (при перекрытии электронных облаков молекулы начинают сильно отталкиваться), чему соответствует член $ - \quad{{\left( {\frac{{\sigma }}{r}} \right)}^{{12}}}.$ Данный конкретный вид потенциала отталкивания (в отличие от вида потенциала притяжения) не имеет теоретического обоснования. Более обоснованной является экспоненциальная зависимость $\exp \left( { - {\gamma }r} \right),$ где параметр ${\gamma } = 2{{J}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ в атомных единицах, а $J$ – потенциал ионизации атома [6]. Однако потенциал отталкивания Леннарда–Джонса более удобен в вычислениях, так как $\quad{{r}^{{12}}} = {{\left( {{{r}^{6}}} \right)}^{2}},$ что и оправдывает его применение.
Для ускорения расчетов потенциал Леннарда–Джонса часто обрывают на расстоянии ${{r}_{c}} = 2.5{\sigma }$ [7]. Выбор ${{r}_{c}} = 2.5{\sigma }$ обусловлен тем, что на этом расстоянии значение энергии взаимодействия составляет лишь $ \approx 0.0163$ от глубины ямы ${\varepsilon }{\text{.}}$
Однако обрывать потенциал таким способом не всегда удобно. А именно, подобный обрыв
означает, что при пересечении молекулой сферы радиуса ${{r}_{c}}$ энергия системы меняется скачком, или (что то же самое) на молекулу действует бесконечно
большая сила. Для того, чтобы избежать этой нефизической ситуации, при обрыве потенциала
его также сдвигают, так что выполняется условие 
(6)
$U\left( r \right) = \left\{ {\begin{array}{*{20}{c}} {4{\varepsilon }\left[ {{{{\left( {\frac{{\sigma }}{r}} \right)}}^{{12}}} - {{{\left( {\frac{{\sigma }}{r}} \right)}}^{6}}} \right] - \quad{{U}_{{LJ}}}\left( {{{r}_{c}}} \right),}&{r \leqslant {{r}_{c}},} \\ {\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad0,}&{r \geqslant {{r}_{c}},} \end{array}} \right.$При моделировании взаимодействия водяного пара и пластинчатой поры использовались следующие параметры потенциала Леннарда–Джонса: $\varepsilon = 6.74 \times {{10}^{{ - 3}}}$ эВ, ${\sigma } = 3.17\,\,\quad{{\AA}}$
Для интегрирования уравнений движения (1) использовался модифицированный метод Верле [8] (Velocity Verlet). Интегрирование производится по следующей схеме.
1. В начале каждого шага задаются или рассчитываются на предыдущем шаге по времени t следующие величины: $r\left( t \right),\,\,\text{v}\left( t \right),\,\,f\left( t \right).$
2. Затем вычисляются значения скоростей частиц в момент времени $t + \frac{{{\Delta }t}}{2}$ и координат нового местонахождения частиц:
3. После этого пересчитываются силы, действующие на частицу в момент времени $t + {\Delta }t{\text{:}}$
4. Далее рассчитываются значения скоростей на следующем шаге:
ОПИСАНИЕ МОДЕЛИРУЕМОЙ СИСТЕМЫ
Моделируемая система состоит из $N = 1\quad250\quad$ молекул воды, что соответствует плотности 100% насыщенного пара при температуре 25°C. Молекулы воды в начальный момент времени равномерно распределены в объеме пластинчатой поры в виде прямоугольника со сторонами 253 × 253 × × 25.3 нм. Внешняя среда моделируется пространством в пять раз большим, чем размер поры.
В начальный момент времени во внешнем пространстве находится 20% насыщенный пар, чему соответствует 1250 молекул воды, которые равномерно распределены во внешнем пространстве. Как уже упоминалось при постановке задачи моделирования, в нашем случае три стенки поры непрозрачные, поэтомумолекулы воды от них отражаются. Остальные три стенки пропускают молекулы воды во внешнее пространство. На открытых границах решения уравнений движения удовлетворяют периодическим краевым условиям. Из-за этого количество молекул в системе с течением времени не меняется (остается постоянным).
В процессе моделирования описанной системы скоростным методом Верле решаются уравнения движения Ньютона с шагом интегрирования ${\Delta }t$ = 0.017 пс. Начальные скорости выбираются случайным образом из интервала (–1; 1). Затем скорости корректируются для того, чтобы начальный полный импульс системы сохранялся равным нулю для обеспечения изотермической эволюции системы пора–водяной пар при температуре, равной 25°C.
Для исследования влияния термостата на процесс моделирования были рассмотрены два случая:
1. Моделирование без использования термостата.
2. Моделирование с использованием термостата Берендсена для контроля изменения температуры внешней среды.
Во внешней среде поддерживалась постоянная (равная начальной) температура. В процессе моделирования на каждом временном шаге (${\Delta }t$ = 1 фм) система приводится в равновесное состояние с использованием термостата Берендсена:
(7)
${\lambda } = {{\left[ {1 + \frac{{\Delta t}}{{\tau }}\left( {\frac{{{{T}_{0}}}}{{T\left( {t - \frac{{\Delta t}}{2}} \right)}} - 1} \right)} \right]}^{{\frac{1}{2}}}}.$Моделирование проводилось для двух миллионов временны́х шагов. В результате было достигнуто общее время эволюции системы равное 0.033266 мкс. Для вычислений сил и ускорений использовался потенциал Леннарда–Джонса (5).
В процессе моделирования исследовались процессы высыхания и намокания поры. Постановка задачи моделирования для случая процесса высыхания приведена выше. Процесс намокания моделировался при следующих начальных условиях. В поре находится 20% насыщенный пар, чему соответствует 250 молекул воды, помещенных в поре данного размера. Во внешнем пространстве находится 100% насыщенный пар, что соответствует 6250 молекулам воды, размещенным во внешнем по отношению к поре пространстве, чтобы обеспечить плотность насыщенного пара 23.09 × 10–18 нг/нм3 вне поры. Остальные параметры имели те же значения, что и в предыдущем случае.
Моделирование проводилось для следующих случаев.
1. Начальная температура 15°С, 100% насыщенному пару в поре соответствует 700 молекул воды и такое же количество молекул во внешнем пространстве в случае 20% насыщенного пара, поскольку внешнее пространство моделировалось объемом, в пять раз бóльшим, чем объем поры с соответствующими граничными. Для процесса намокания при тех же условиях в поре размещается 140, а во внешнем объеме – 3500 молекул воды.
2. Начальная температура 35°С, в процессе высыхания в поре размещается 2160 молекул воды, во внешнем объеме – такое же количество. При обратном процессе внутри поры находится 432, а во внешнем объеме – 10 800 молекул воды.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
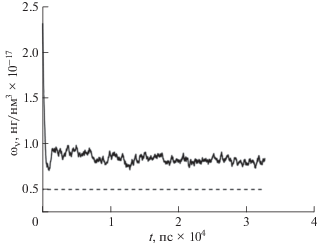
На следующих графиках представлена зависимость величины плотности водяного пара в поре от времени. В первом случае (рис. 1а) эволюция системы происходит без термостатирования. Во втором (рис. 1б) эволюция системы происходит при включенном термостате Берендсена. На рис. 2 представлены результаты моделирования для 100 000 временны́х шагов. Сплошная кривая получена в результате моделирования, прерывистая прямая – средняя плотность, которая соответствует указанному количеству молекул и указанным размерам всей системы.
Рис. 1.
Плотность водяного пара в поре в зависимости от времен: а – моделирование без использования термостата, б – моделирование с использованием термостата Берендсена для контроля температуры в поре.
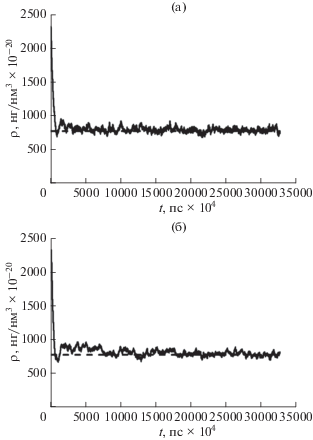
Рис. 2.
Эволюция плотности водяного пара в поре с использованием термостата Берендсена в течение 100 000 временны́х шагов.
Графики, показанные на рис. 3, демонстрируют зависимость величины диффузионного коэффициента от времени. Сплошная кривая представляет зависимость коэффициента диффузии внешней среды, а прерывистая кривая – зависимость диффузионного коэффициента от времени в поре.
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ НА ОСНОВЕ МАКРОСКОПИЧЕСКОЙ ДИФФУЗИОННОЙ МОДЕЛИ
При использовании результатов моделирования методом молекулярной динамики, приведенными
в предыдущем разделе, получены следующие результаты решения уравнений макроскопической
модели. Временной интервал равен $0 \leqslant t \leqslant 33{\kern 1pt} 266$ пс. Начальная концентрация внутри поры равна ${{{\omega }}_{{\text{v},0}}}$ = 2.304 × $\frac{{{{{10}}^{{ - 17}}}\,\,{\text{н
г
}}}}{{{\text{н
}}{{{\text{м
}}}^{3}}}}.$ Параметр, характеризующий сопротивление переносу водяного пара в воздухе, равен ${\beta }$ = 0.05 × 109 м/с. Начальная концентрация водяного пара вне поры равна ${{\omega }_{{\text{v},{\text{out}}}}}$ = 0.4608 × 10–17 нг/нм3, что соответствует относительной влажности ${\varphi } = 0.2.$ И наконец, усредняя результаты молекулярно-динамического моделирования, приведенные
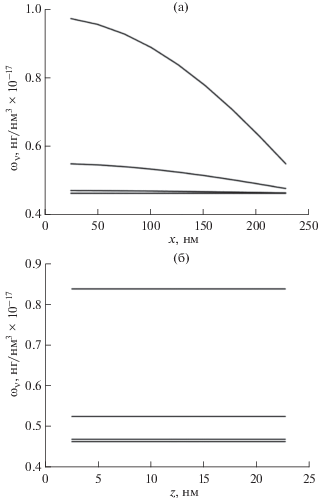
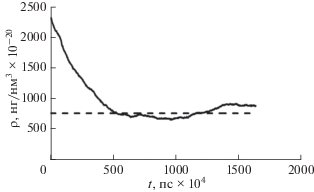
на рис. 3, получим значение диффузионного коэффициента  нм2/пс. Далее, усредняя решение уравнения (2) по пространству, получаем среднюю концентрацию ${{{\omega }}_{\text{v}}}\left( t \right),$ сравнимую с плотностью в поре (рис. 4).
нм2/пс. Далее, усредняя решение уравнения (2) по пространству, получаем среднюю концентрацию ${{{\omega }}_{\text{v}}}\left( t \right),$ сравнимую с плотностью в поре (рис. 4).
Результаты расчетов концентрации водяного пара в поре на основе макроскопической диффузионной модели приведены на рис. 5.
ЗАКЛЮЧЕНИЕ
В данной работе проведен сравнительный анализ различных подходов к моделированию поведения водяного пара в пластинчатой поре. Моделирование проводилось тремя способами. Первый способ основан на использовании метода классической молекулярной динамики. Второй использует решение уравнений макроскопической диффузионной модели. И третий способ реализует применение гибридного подхода, состоящего в решении уравнений диффузионной модели с использованием значений коэффициента диффузии, полученных в результате молекулярно-динамического моделирования. Анализ результатов расчетов показал, что расчеты на основе гибридного подхода являются более точными, чем расчеты на основе макроскопической диффузионной модели с использованием постоянного эмпирического коэффициента диффузии.
Список литературы
Rouquerol J., Avnir D.D., Fairbridge C.W. et al. // Pure Appl. Chemist. V. 661994. P. 1739.
McNaught A.D., Wilkinson A. IUPAC. Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”). Oxford: Blackwell Scientific Publications, 1997. 355 p.
Gould H., Tobochnik J., Christian W. An Introduction to Computer Simulation Methods. Third edition, Addison Valley: Pearson, 2006. 813 p.
Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики. М.: Наука, 1977. 224 с.
Lennard-Jones J.E. // Proc. Roy. Soc. 1924 .V. A106. P. 463.
Смирнов Б.М. // УФН. 1992. Т. 162. № 12. С. 97.
Allen M.P., Tildesley D.J. Computer Simulation of Liquids. New York: Oxford University Press, 1989. 385 p.
Verlet L. // Phys. Rev. 1967. V. 159. P. 98.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования