Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 10, стр. 74-78

1. ВВЕДЕНИЕ

Полимерные материалы, обладают уникальными и привлекательными для применений свойствами, такими как малый вес, высокая прочность, способность противостоять агрессивным химическим средам, простота обработки. Однако полимеры, в основном, являются изоляторами. Если бы каким-то образом можно было существенно повысить проводимость традиционных полимеров, это открыло бы большие перспективы для использования таких материалов во многих новых областях, где их использование пока ограничено. К таким областям относится производство органических фотоэлементов, фотодиодов, химических и биосенсоров [1].

В последние три десятилетия, после разработки надежных способов получения углеродных нано-объектов, таких, например, как углеродные нанотрубки и углеродные графеноподобные нанофлейки, усилия исследователей сосредоточены на получении проводящих нанокомпозитов на основе полимеров путем диспергирования углеродных наполнителей.

Проводимость полимер-углеродных нанокомпозитов зависит от многих факторов, включая тип полимера, плотность наполнителя, технику приготовления нанокомпозита, тип и геометрию пересечения углеродных нанотрубок (УНТ). Зависимость от большого количества параметров приводит к тому, что проводимость нанокомпозитов изменяется в очень широких пределах [2]. В этих условиях экспериментальные исследования с целью поиска нанокомпозитов с оптимальными свойствами могут быть весьма длительными и дорогостоящими, и, следовательно, возрастает актуальность количественного, предсказательного моделирования характеристик нанокомпозитов.

Моделирование проводимости полимер-углеродных нанокомпозитов – это многомасштабная задача, включающая определение пространственного положения полимера вблизи контактов нанообъектов, расчета контактного сопротивления пересечений нанообъектов, заполненных полимером, решение перколяционной задачи и вычисление удельной проводимости композита.

В настоящей работе мы сосредоточились на исследовании наиболее сложной составляющей из перечисленных задач – разработке простого и эффективного алгоритма для выбора элементов перколяционного кластера, участвующих в проводимости. Несмотря на большое количество работ, посвященных данному вопросу [3, 4, 8–10], в этой области остаются еще нерешенные вопросы. Существующие методы определения необходимых элементов либо сложны в реализации, как разложение Дюльмаг–Мендельсона [3], либо неэффективны с точки зрения временны́х затрат, как методы, основанные на случайных блужданиях на графе без повторений [4]. Кроме того, в большинстве публикаций на тему проводимости в системе УНТ отсутствует явное, подробное описание метода решения данной задачи.

В данной статье мы предлагаем метод нахождения элементов перколяционного кластера, участвующих в проводимости, сочетающий простоту и эффективность, основанный на рекурсивном удалении тупиковых конфигураций кластера. Все шаги алгоритма детально описаны, что позволяет легко воспроизвести наши результаты. Разработанный метод может быть в дальнейшем применен для расчетов удельной проводимости полимер-углеродных нанокомпозитов.

2. МЕТОДИКА МОДЕЛИРОВАНИЯ

Рассмотрим первый этап решения задачи о проводимости УНТ – этап формирования перколяционного кластера. Для формирования кластера была выделена область – куб с размерами L × L × L. Далее, по стандартному сценарию в куб последовательно добавлялись объекты до фиксированного значения плотности их в кубе – $\eta $. В качестве объектов заполнения в данной задаче выбраны капсулы (цилиндр с двумя полусферами на торцах). Этот выбор обусловлен двумя факторами: с одной стороны капсулы довольно хорошо отражают геометрическую форму УНТ, с другой стороны – условие пересечения таких объектов выглядит весьма просто: капсулы пересекаются, если расстояние между образующими этих цилиндров меньше их диаметра ($\rho < 2r$). Мы рассматриваем полностью проницаемые объекты одинаковых размеров. Задача перколяции с полностью проницаемой оболочкой для капсул была рассмотрена в [5]. Также, в работе [6] была рассмотрена задача частично проницаемой оболочки.

Образование перколяционного кластера может быть отслежено на этапе его формирования с помощью адаптированного под континуальную перколяцию алгоритма Ньюмена и Зиффа [7]. Здесь, как и в [8] были использованы периодические граничные условия, а формирование кластера отслеживалось только в z-направлении. Как было отмечено выше, использованный алгоритм работает до тех пор, пока не достигнута фиксированная плотность капсул в кубе:

где $r$ – радиус цилиндра, $h$ – высота. Таким образом, выходом перколяционной задачи является информация о том – сформировался или не сформировался перколяционный кластер. В случае если кластер сформировался, нам доступна следующая информация:

1. Массив всех существующих связей объектов в системе.

2. Номера капсул, принадлежащих перколяционному кластеру.

3. Номера всех граничных связей (отвечающих периодическим граничным условиям).

Второй этап решения задачи о проводимости УНТ сводится к формированию резисторной сети из элементов перколяционного кластера, полученных на предыдущем этапе, и решению матричной задачи, отражающей законы проводимости для заданной конфигурации сети под приложенным к границам системы напряжением. Падение напряжения происходит на каждой УНТ, между двумя узлами. Здесь узлом названа область пересечения двух УНТ. В данной задаче была принята “точечная модель”, и размер области пересечения УНТ не принимался во внимание. Такое приближение возможно для систем с УНТ, длина которых много больше их диаметра, т.е. систем с большими аспектными отношениями.

Для определенности будем считать, что напряжение приложено к нижней и верхней грани куба (плоскости z = 0 и z = L). Тогда напряжения в узлах уменьшаются от максимального значения (верхняя грань) до минимального значения (нижняя грань) [9]. Поскольку напряжение на каждой границе системы – константа, все граничные элементы для каждой грани могут быть объединены в единственный граничный узел. Такой шаг позволяет избежать поиска [10] распределения токов между граничными элементами. В этом случае входной и выходной безразмерные токи всегда можно задать как 1 и –1.

Кроме того, в работе [8] было показано, что использование периодических граничных условий позволяет производить расчет на системах меньшего размера, ($L \sim l$, где $l = h + 2r$ – длина капсулы) поскольку объем моделирования в этом случае не влияет на конечную проводимость системы. Это преимущество также было использовано в нашей работе.

Далее рассматривается этап выбора элементов из перколяционного кластера, участвующих в проводимости. Важно отметить, что существуют работы, где этот этап пропущен. Однако расчет системы с большими аспектными отношениями, что чаще всего встречается в экспериментах, предполагает массивы большой размерности. Для аспектных отношений более 100 эти массивы могут содержать сотни тысяч элементов. Следовательно, уменьшение размерности важно для того, чтобы сделать расчет более быстрым. В работах, где этот этап осуществлен, используется преимущественно разложение Дюльмаг–Мендельсона [3]. В отличие от большинства ранних работ, которые на данном этапе используют разложение Дюльмаг–Мендельсона [8, 10, 11], мы реализуем следующий шаг без обозначенной выше процедуры. Это связано со сложностью ее программной реализации. Также решение задачи о проводимости УНТ может быть получено с помощью обычного поиска всевозможных путей из одной точки графа в другую – блуждания на графе без повторений [4], однако, такое решение является не самым эффективным с точки зрения времени, затрачиваемого на вычисление. Предложенный нами сценарий реализации алгоритма более прост в исполнении, и не требует использования специальных библиотек.

Идея заключается в следующем: используя полученные выше массивы, так называемые “тупиковые” ветви могут быть рекурсивно удалены из кластера. В таком случае конфигурации типа “петель”, которые не дают вклада в проводимость, не будут удалены. Однако их наличие, никак не влияет на конечный результат.

Таким образом, для удаления элементов, не участвующих в переносе тока, и составления матрицы проводимости и вектора токов необходимо:

1) удалить из масcива всех связей номера объектов, не участвующих в перколяции;

2) рекурсивно удалить из массива все элементы, имеющие только одну связь (кроме граничных);

3) на каждой границе объединить все узлы, так как поверхность эквипотенциальна.

Из полученного таким образом массива может быть составлена матрица проводимости. Для каждого элемента определяются те элементы, с которым связан (пересекается) данный. Эта информация соответствует строке матрицы (в теории графов это называется матрицой смежности). Далее, для всех внутренних элементов к матрице применяется закон Кирхгоффа [12]. Полученная симметричная матрица является матрицей проводимости. Кроме нее, необходимо сформировать вектор токов. Как уже было отмечено выше, число граничных элементов может быть сведено к двум. Для этих элементов вектора значения будут равны 1 и –1, соответственно, остальные элементы вектора равны нулю. После того как матричная задача сформирована, мы используем библиотеку LAPACK (библиотека с открытым исходным кодом) [13] для решения системы линейных алгебраических уравнений. В результате из полученного вектора напряжений рассчитываем проводимость:

4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Описанная в разделе 2 процедура выполняется для каждой фиксированной плотности УНТ (η), в том случае, если перколяционный кластер сформирован. Если кластер не сформировался, проводимость равна нулю. Таким образом, была проведена серия испытаний (количество испытаний составило 1000) для каждой фиксированной плотности. Программный код был реализован на языке Фортран с использованием библиотеки LAPACK для решения системы линейных алгебраических уравнений.

Задача проводимости сначала была решена для модельного случая. На рис. 1 представлены результаты моделирования – проводимость системы с параметрами L = 25 мкм, a = 1, R_CNT = 1 МОм в обычном и логарифмическом масштабах. Порог перколяции такой системы был оценен как η_с = 0.24.

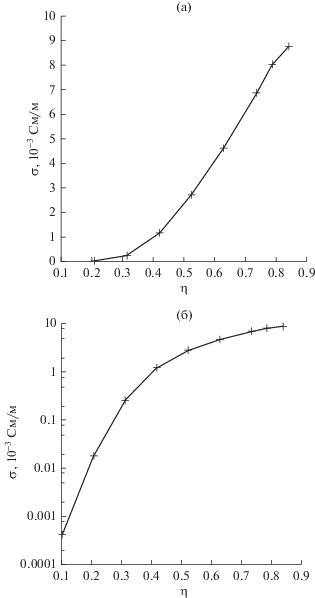
Из рис. 1а, 1б видно, что основной рост проводимости приходится на область концентраций вблизи порога перколяции и в представленном случае составил четыре порядка.

Модельная задача позволяет качественно понять поведение системы. Однако, гораздо больший интерес с точки зрения эксперимента представляют системы с большими аспектными отношениями. Для сравнения с реальными экспериментами была промоделирована система с параметрами L = 15 мкм, a = 100, R_CNT = 1 МОм (рис. 2). Порог перколяции такой системы также был оценен: η_с = 0.007. Основной рост проводимости также приходится на область около порога перколяции, и здесь наблюдалось увеличение проводимости на 3–4 порядка. Полученные результаты были сопоставлены с данными из экспериментов работ [14, 15]. Как видно из графика – полученные результаты весьма неплохо согласуются с представленными экспериментальными значениями.

5. ВЫВОДЫ

В работе предложен простой и эффективный алгоритм расчета проводимости для систем углеродных нанотрубок. Алгоритм основан на рекурсивном удалении элементов перколяционного кластера, не участвующих в проводимости. Представленный метод прост в реализации и не требует больших временны́х затрат (сопоставим по времени работы с существующими алгоритмами, основанными на разложении Дюльмаг–Мендельсона). Полученные с использованием данного алгоритма значения проводимости системы из УНТ с аспектным отношением a = 100 хорошо согласуются с экспериментальными данными, представленными в работах [14, 15]. Таким образом, можно сделать вывод о пригодности данного алгоритма для расчетов с количественной точностью проводящих свойств систем УНТ. В дальнейшем предложенная методика расчета проводящих свойств систем УНТ будет применена для расчета проводимости различных нанокомпозитных полимерных материалов.