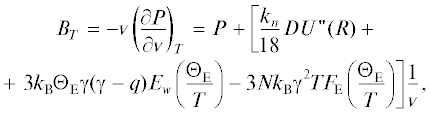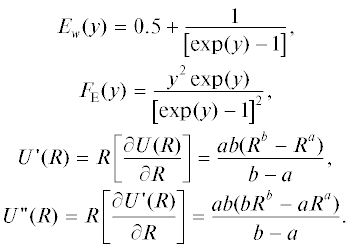Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 11, стр. 88-100
Вычисление поверхностной энергии кристалла и ее зависимости от температуры и давления
М. Н. Магомедов *
Институт проблем геотермии и возобновляемой энергетики – филиал Объединенного института
высоких температур РАН
367030 Махачкала, Россия
* E-mail: mahmag4@mail.ru
Поступила в редакцию 26.02.2020
После доработки 16.03.2020
Принята к публикации 20.03.2020
Аннотация
Исходя из параметров парного потенциала межатомного взаимодействия Ми–Леннард-Джонса, разработан метод расчета удельной поверхностной энергии σ, изохорной и изобарной производных функции σ по температуре и изотермической производной функции σ по давлению. Показано, что метод применим как для макро-, так и для нанокристалла с заданным числом атомов и с определенной формой поверхности. Для реализации этого метода параметры парного межатомного потенциала были определены самосогласованным способом на основе термоупругих свойств кристалла. Метод был апробирован на макрокристаллах Fe, Au, Nb, Ta, Mo, W при различных температурах и показал хорошее согласие с экспериментальными данными. На примере ОЦК-Ta изучены изменения поверхностных свойств при уменьшении размера нанокристалла вдоль изотерм T = 10, 300, 2500 K. Показано, что при высоких давлениях и низких температурах функция σ может возрастать при изоморфо-изотермо-изобарическом уменьшении размера нанокристалла.
ВВЕДЕНИЕ
На сегодняшний день предложено несколько методов для расчета удельной поверхностной энергии σ кристалла простого (однокомпонентного) вещества (например, [1–10]). Но большинство из этих методов (например, [1, 5, 6, 8]) работают только при нулевой температуре (T = 0 K) и нулевом давлении (P = 0). Поэтому актуальным является вопрос о зависимости величины σ от P–T-условий, в которых находится кристалл.
В работах [2–4, 7, 9, 10] были предложены различные методы расчета производной функции σ по температуре: σ'(T) = (∂σ/∂T). Но из-за отсутствия в этих работах уравнения состояния, осталось неясным – является ли предложенное в этих работах выражение для σ'(T) изохорной (σ'(T)v) или изобарной (σ'(T)P) производной?
Что касается зависимости поверхностной энергии от давления, то выражения для расчета функции σ '(P) = (∂σ/∂P)T в литературе пока нет, и поэтому оценок этой величины никто не проводил. Проблема связана с тем, что в теоретических моделях, в рамках которых рассчитывалась функция σ, уравнение состояния кристалла с поверхностью получено не было. Между тем зависимость σ(P) необходима при изучении как возникновения трещин при барическом воздействии на макрокристалл, так и для получения уравнения состояния нанокристалла.
В связи с этим, в данной работе будет предложен метод, позволяющий с единых позиций, исходя из парного потенциала межатомного взаимодействия, рассчитать, как уравнение состояния, так и величину σ при произвольных P–T-условиях. Показано, что метод применим как для макро-, так и для нанокристалла с заданным числом атомов N и с определенной формой поверхности. Метод позволяет вычислять производные функции σ по температуре как при изохорических, так и при изобарических условиях. Метод позволяет также изучить производные функции σ по температуре и давлению для нанокристалла из N атомов в различных P–T-условиях.
МЕТОД РАСЧЕТА ПОВЕРХНОСТНЫХ СВОЙСТВ
Рассмотрим наносистему из N одинаковых атомов, ограниченную поверхностью, которая имеет площадь Σ. Изменение свободной энергии Гельмгольца (FH) такой системы при вариации температуры, объема V, числа атомов и площади поверхности обычно представляют в виде [11, 12]:
(1)
$\begin{gathered} d{{F}_{H}} = {{\left( {\frac{{\partial {{F}_{H}}}}{{\partial T}}} \right)}_{{N,V,\Sigma }}}dT + {{\left( {\frac{{\partial {{F}_{H}}}}{{\partial V}}} \right)}_{{N,T,\Sigma }}}dV + \\ + \,\,{{\left( {\frac{{\partial {{F}_{H}}}}{{\partial N}}} \right)}_{{T,V,\Sigma }}}dN + {{\left( {\frac{{\partial {{F}_{H}}}}{{\partial \Sigma }}} \right)}_{{N,V,T}}}d\Sigma = \\ = - SdT - PdV + {{{\mu }}_{g}}dN + \sigma d\Sigma , \\ \end{gathered} $Если число атомов в системе не изменяется, то выражение для dFH можно преобразовать к виду:
(2)
$d{{f}_{H}} = d\left( {\frac{{{{F}_{H}}}}{N}} \right) = - sdT - Pd{v} + \sigma d\left( {\frac{\Sigma }{N}} \right),$Из формулы (2) легко видеть, что удельная поверхностная энергия равна:
Но при N = const нельзя изоморфно изменить площадь поверхности, не изменив при этом объем, так как при постоянной форме нанокристалла они связаны соотношением: Σ ∼ V 2/3. Поэтому, как это было указано в [13, 14], при Σ/N ≠ 0 определить функцию σ можно только путем изохорно-изотермической обратимой деформации формы наносистемы, т.е. из выражения:
(3)
$\begin{gathered} \sigma (T,{v},N,f) = {{\left( {\frac{{\partial {{f}_{H}}}}{{\partial ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}} \right)}_{{T,N,{v}}}} = \\ = {{{{{\left( {\frac{{\partial {{f}_{H}}}}{{\partial f}}} \right)}}_{{T,N,{v}}}}} \mathord{\left/ {\vphantom {{{{{\left( {\frac{{\partial {{f}_{H}}}}{{\partial f}}} \right)}}_{{T,N,{v}}}}} {{{{\left( {\frac{{\partial ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}{{\partial f}}} \right)}}_{{T,N,{v}}}}}}} \right. \kern-0em} {{{{\left( {\frac{{\partial ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}{{\partial f}}} \right)}}_{{T,N,{v}}}}}}, \\ \end{gathered} $Из (2) видно, что давление в наносистеме должно вычисляться по формуле:
(4)
$P(T,{v},N) = - {{\left( {\frac{{\partial {{f}_{H}}}}{{\partial {v}}}} \right)}_{{T,N,\Sigma }}}.$Но при постоянных значениях T, N и Σ невозможно изменить удельный объем ограниченной поверхностью системы. Поэтому, для того чтобы обойти данную неопределенность, будем далее определять давление как изменение удельной свободной энергии Гельмгольца при вариации удельного объема при N и T = const, и полагая, что поверхность системы является геометрической поверхностью, не имеющей объема.
Это допущение позволит представить свободную энергию в виде [11]:
(5)
$\begin{gathered} {{F}_{H}}(T,{v},N,f) = {{F}_{{H{\text{ }}in}}}(T,{v}) + \\ + \,\,\sigma (T,c,N,f)\Sigma (c,N,f). \\ \end{gathered} $При этом площадь поверхности Σ(c, N, f) здесь является площадью гладкой геометрической поверхности, которую называют поверхностью Гиббса [11, 12].
Таким образом, используя (5), определим давление в наносистеме выражением следующего вида:
(6)
$\begin{gathered} P(T,{v},N,f) = - {{\left( {\frac{{\partial {{f}_{H}}}}{{\partial {v}}}} \right)}_{{T,N}}} = \\ = {{P}_{{in}}}(T,{v}) - {{P}_{{sf}}}(T,c,N,f). \\ \end{gathered} $Здесь Pin –“объемное” давление, т.е. давление, определяемое без учета поверхностного члена в (2) и в (5):
(7)
${{P}_{{in}}}(T,{v}) = - \mathop {\lim }\limits_{N \to \infty } {{\left[ {\frac{{\partial {{f}_{{H,\,in}}}}}{{\partial {v}}}} \right]}_{{T,N}}}.$Функция Psf – поверхностное давление, которое равно [14, 15]:
(8)
${{P}_{{sf}}}(T,c,N,f) = {{\left[ {\frac{{\partial \left( {{{\sigma \Sigma } \mathord{\left/ {\vphantom {{\sigma \Sigma } N}} \right. \kern-0em} N}} \right)}}{{\partial {v}}}} \right]}_{{T,N}}} = {{P}_{{ls}}}(1 - {{\Delta }_{p}}).$Первый сомножитель в (8) – давление Лапласа, которое определяется изменением площади поверхности с изменением объема для наносистемы в вакууме:
(9)
$\begin{gathered} {{P}_{{ls}}}(T,{v},N,f) = \sigma {{\left[ {\frac{{\partial \left( {{\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N}} \right)}}{{\partial {v}}}} \right]}_{{T,N}}} = \\ = \sigma \left( {\frac{{{\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N}}}{{v}}} \right){{\left[ {\frac{{\partial \ln ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}{{\partial \ln ({v})}}} \right]}_{{T,N}}}. \\ \end{gathered} $Выражение для функции Δp из формулы (8) имеет вид:
(10)
${{\Delta }_{p}} = - {{\left[ {\frac{{\partial \ln (\sigma )}}{{\partial \ln ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}} \right]}_{{T,N}}}.$Для жидкой фазы выполняется: (∂σ/∂Σ)T,N = 0. Это обусловлено динамической природой жидкого состояния, где большая доля атомов находится в делокализованном состоянии. Изотермическое растяжение площади “гиббсовской” поверхности жидкой фазы вызывает приток к ее поверхности новых атомов из объема. Если приток атомов к поверхности происходит со скоростью, достаточной для того, чтобы поверхностная плотность атомов сохранялась неизменной, то величина σ для жидкой фазы не будет меняться с ростом Σ, и значение Δp будет равным нулю. Именно поэтому условие: Δp = 0, как это было показано в [16], можно использовать в качестве “поверхностного” критерия фазового перехода кристалл–жидкость для системы с геометрической поверхностью Гиббса.
Для твердой фазы считать Δp = 0 нельзя. На это впервые было указано в работе [17]. Причем, наличие функции Δp в формуле (8) приводит к эффектам, присущим только твердой фазе наносистемы [7, 8]:
1) так как Δp > 0, то для нанокристалла всегда выполняется: Psf < Pls;
2) если Δp > 1, то поверхностное давление становится растягивающим: Psf < 0;
3) при плавлении нанокристалла поверхностное давление резко возрастает.
Если кристаллическая структура (характеризуемая коэффициентом упаковки kp) и форма поверхности (характеризуемая управляющим формой параметром f ) не изменяются при изотермической вариации удельного объема, то функции Pls и Δp из (9) и (10) примут вид:
(11)
${{P}_{{ls}}} = \sigma \left( {\frac{{{\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N}}}{{v}}} \right){{\left[ {\frac{{\partial \ln ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}{{\partial \ln ({v})}}} \right]}_{{T,N,{{k}_{p}},f}}} = \frac{2}{3}\sigma \left( {\frac{{{\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N}}}{{v}}} \right),$(12)
${{\Delta }_{p}} = - {{\left[ {\frac{{\partial \ln (\sigma )}}{{\partial \ln ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}} \right]}_{{T,N}}} = - \frac{1}{2}{{\left[ {\frac{{\partial \ln (\sigma )}}{{\partial \ln (c)}}} \right]}_{{T,N,{{k}_{p}},f}}}.$Таким образом, для дальнейших расчетов необходимо, используя формулу (3), определить функцию σ(T, c, N, f). Для этого необходимо принять некую геометрическую модель нанокристалла с варьируемой формой поверхности.
ГЕОМЕТРИЧЕСКАЯ МОДЕЛЬ НАНОКРИСТАЛЛА
Как и в работах [13–16, 18, 19] положим, что нанокристалл со свободной поверхностью имеет вид прямоугольного параллелепипеда с квадратным основанием, ограненный гранями типа (100) с геометрической поверхностью Гиббса. Если в решетке нанокристалла простого вещества содержится Nv вакансий, однородно распределенных по объему, то первое координационное число (т.е. число ближайших атомов) для атома в объеме нанокристалла равно [14, 18, 19]:
(13)
${{k}_{n}}(\infty ) = \frac{{k_{n}^{{\text{o}}}(\infty )N}}{{N + {{N}_{{v}}}}} = k_{n}^{{\text{o}}}(\infty )(1 - {{\phi }_{{v}}}),$Величина f = Nps/Npo = ${{N_{{ps}}^{{\text{o}}}} \mathord{\left/ {\vphantom {{N_{{ps}}^{{\text{o}}}} {N_{{po}}^{{\text{o}}}}}} \right. \kern-0em} {N_{{po}}^{{\text{o}}}}}$ – параметр формы, который определяется отношением числа $N_{{ps}}^{{\text{o}}}$ атомов (или Nps = $N_{{ps}}^{{\text{o}}}$/(1 – ϕv)1/3 ячеек) на боковом ребре к числу $N_{{po}}^{{\text{o}}}$ атомов (или Npo = = $N_{{po}}^{{\text{o}}}$/(1 – ϕv)1/3 ячеек) на ребре основания. Очевидно, что для стержневидной формы f > 1, для куба f = 1, для пластинчатой формы f < 1.
Число ячеек и число атомов в нанокристалле определенной формы равно:
(14)
$\begin{gathered} N + {{N}_{{v}}} = f\frac{{N_{{po}}^{3}}}{\alpha } = f\frac{{{{{\left( {N_{{po}}^{{\text{o}}}} \right)}}^{3}}}}{{\alpha (1 - {{\phi }_{{v}}})}}, \\ N = f\frac{{{{{\left( {N_{{po}}^{{\text{o}}}} \right)}}^{3}}}}{\alpha }, \\ \end{gathered} $Число атомов и параметр формы в этой модели могут изменяться в пределах:
Ограничение системы поверхностью приведет к обрыву связей на границе. Поэтому, если использовано приближение “взаимодействия только ближайших соседей”, то вместо первого координационного числа kn необходимо брать функцию 〈kn〉, которая есть среднее (по всей наносистеме) значение первого координационного числа. Очевидно, что функция 〈kn〉 зависит как от размера, так и от формы наносистемы. При этом структуру наносистемы полагаем неизменной: kp = const. Данная модель нанокристалла в виде прямоугольного параллелепипеда (Rectangular Parallelepiped), форму которого можно варьировать с помощью параметра формы f, была названа в работах [13–16] RP-моделью. Аналогичная модель из N + Nv ячеек была названа в [18, 19] RP(vac)-моделью.
В рамках RP(vac)-модели зависимость нормированного среднего значения первого координационного числа от N + Nv и f описывается выражением [18]:
(15)
$\begin{gathered} k_{n}^{*} = \frac{{\left\langle {{{k}_{n}}(N + {{N}_{{v}}},f)} \right\rangle }}{{{{k}_{n}}(\infty )}} = 1 - Z{}_{s}(f) \times \\ \times \,\,{{\left( {\frac{{{{\alpha }^{2}}}}{{N + {{N}_{{v}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} = 1 - Z{}_{s}(f){{\left( {\frac{{{{\alpha }^{2}}}}{N}(1 - {{\phi }_{{v}}})} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}, \\ \end{gathered} $Входящая в (15) функция формы: Zs(f) = (1 + 2 f)/ /(3f 2/3), достигает минимума равного единице при f = 1, т.е. для системы в форме куба. Для пластинчатых (f < 1) или стержневидных (f > 1) форм значение функции формы больше единицы: Zs(f ≠ 1) > 1. Поэтому функция kn(f)* при любом значении N атомов (или N + Nv ячеек) имеет максимум при f = 1, т.е. для наиболее энергетически оптимальной – кубической формы прямоугольного параллелепипеда.
Объем и площадь поверхности для RP(vac)-модели равны:
(16)
$\begin{gathered} V = {{{{{\left( {N_{{po}}^{{\text{o}}}} \right)}}^{{\text{3}}}}f{{c}^{{\text{3}}}}~} \mathord{\left/ {\vphantom {{{{{\left( {N_{{po}}^{{\text{o}}}} \right)}}^{{\text{3}}}}f{{c}^{{\text{3}}}}~} {({\text{1}}--{{\phi }_{{v}}})}}} \right. \kern-0em} {({\text{1}}--{{\phi }_{{v}}})}} = \\ = (N + {{N}_{{v}}})\alpha {{c}^{{\text{3}}}} = \\ = {{\left( {N_{{po}}^{{\text{o}}}} \right)}^{{\text{3}}}}fc_{{\text{o}}}^{{\text{3}}},\,\,\,\, \\ \Sigma = {\text{6}}{{c}^{{\text{2}}}}{{\alpha }_{s}}{{[(N + {{N}_{{v}}})\alpha ]}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{Z}_{s}}\left( f \right) = \\ = {\text{6}}c_{{\text{o}}}^{{\text{2}}}{{\alpha }_{s}}{{(N\alpha )}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{Z}_{s}}\left( f \right), \\ \end{gathered} $Кубическая форма может реализовываться только при определенном числе ячеек, из которого можно построить куб: (N + Nv)cub = ${{\left( {N_{{po}}^{{\text{o}}}} \right)}^{{\text{3}}}}$/[α(1 – ϕv)], где $N_{{po}}^{{\text{o}}}$ = 2, 3, 4, …. При “некубичном” значении числа ячеек: N + Nv ≠ (N + Nv)cub, параллелепипед может иметь либо пластинчатую, либо стержневидную форму, причем выполняется неравенство: kn((N + Nv)cub ± 1)* < ${{k}_{n}}(N + {{N}_{{v}}})_{{{\text{cub}}}}^{*}.$
Таким образом, изоморфная (т.е. рассчитанная при f = const) зависимость kn(N + Nv) монотонно уменьшается при N + Nv → Nmin = = INT[23/α], но общая зависимость kn(N + Nv) имеет осциллирующий вид с максимумами в точках kn(N + Nv)cub, соответствующих нанокристаллам с кубической формой, и с минимумами при таких значениях N + Nv ≠ (N + Nv)cub, из которых можно построить только бездефектный стержень биатомной толщины. А так как многие свойства нанокристалла определяются именно значением kn(N), то зависимость этих свойств от N также будет иметь осциллирующий вид. Поэтому изоморфная производная (∂kn/∂N)f не будет иметь никаких особенностей, чего нельзя сказать о неизоморфной производной (∂kn /∂N)x≠f.
В рамках RP(vac)-модели удельная поверхностная энергия грани (100) и давление Лапласа определяются выражениями вида:
(17)
$\begin{gathered} \sigma = {{{{{\left( {\frac{{\partial {{f}_{H}}}}{{\partial k_{n}^{*}}}} \right)}}_{{T,N,c}}}{{{\left( {\frac{{\partial k_{n}^{*}}}{{\partial {{Z}_{s}}(f)}}} \right)}}_{{N,{{k}_{p}}}}}} \mathord{\left/ {\vphantom {{{{{\left( {\frac{{\partial {{f}_{H}}}}{{\partial k_{n}^{*}}}} \right)}}_{{T,N,c}}}{{{\left( {\frac{{\partial k_{n}^{*}}}{{\partial {{Z}_{s}}(f)}}} \right)}}_{{N,{{k}_{p}}}}}} {{{{\left( {\frac{{\partial ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}{{\partial {{Z}_{s}}(f)}}} \right)}}_{{N,c,{{k}_{p}}}}}}}} \right. \kern-0em} {{{{\left( {\frac{{\partial ({\Sigma \mathord{\left/ {\vphantom {\Sigma N}} \right. \kern-0em} N})}}{{\partial {{Z}_{s}}(f)}}} \right)}}_{{N,c,{{k}_{p}}}}}}} = \\ = \frac{{ - (1 - {{\phi }_{{v}}})}}{{6{{c}^{2}}{{\alpha }_{s}}}}{{\left( {\frac{{\partial {{f}_{H}}}}{{\partial k_{n}^{*}}}} \right)}_{{T,N,c}}}, \\ \end{gathered} $(18)
$\begin{gathered} {{P}_{{ls}}} = \frac{{2\Sigma }}{{3V}}\sigma = \frac{{4{{\alpha }_{s}}{{Z}_{s}}(f)}}{{{{{[\alpha (N + {{N}_{{v}}})]}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}c(N,f)}}\sigma = \\ = 4{{\alpha }_{s}}\frac{{(1 - k_{n}^{*})}}{{\alpha c(N,f)}}\sigma {\text{.}} \\ \end{gathered} $В “термодинамическом пределе” (т.е. когда N → ∞ и V → ∞ при v = V/N = const), согласно (15), имеем: kn(N → ∞)* → 1. При этом функция σ стремится к значению σ(N = ∞), а функции Pls из (18) и Psf из (11) исчезают.
Таким образом, для вычисления функции σ(T, c, N, f) с помощью (17) необходимо определить зависимость удельной свободной энергии Гельмгольца fH от трех аргументов: T, c и $k_{n}^{*}.$
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДЛЯ RP-МОДЕЛИ
Пусть взаимодействие атомов в нанокристалле простого однокомпонентного вещества описывается парным четырехпараметрическим потенциалом Ми–Леннарда-Джонса, который имеет следующий вид [12, 14]:
(19)
$\varphi (r) = \frac{D}{{(b - a)}}\left[ {a{{{\left( {\frac{{{{r}_{{\text{o}}}}}}{r}} \right)}}^{b}} - b{{{\left( {\frac{{{{r}_{{\text{o}}}}}}{r}} \right)}}^{a}}} \right],$Для простоты допустим, что нанокристалл не содержит вакансий и диффундирующих атомов. Тогда, используя для колебательного спектра нанокристалла модель Эйнштейна и приближение “взаимодействия только ближайших соседей”, для удельной свободной энергии Гельмгольца RP-модели можно принять [12, гл. 8]:
(20)
$\begin{gathered} \frac{{{{f}_{H}}}}{{{{k}_{n}}(\infty )}} = \left( {\frac{{k_{n}^{*}}}{2}} \right)DU(R) + 3\frac{{{{k}_{{\text{B}}}}{{\Theta }_{{\text{E}}}}}}{{{{k}_{n}}(\infty )}} \times \\ \times \,\,\left\{ {\frac{1}{2} + \left( {\frac{T}{{{{\Theta }_{{\text{E}}}}}}} \right)\ln \left[ {1 - \exp \left( { - \frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right)} \right]} \right\}. \\ \end{gathered} $Здесь kB – постоянная Больцмана, ΘE – это температура Эйнштейна, которая связана с температурой Дебая соотношением [12, 20]: Θ = = (4/3)ΘE; R = ro/c – относительная линейная плотность кристалла, U(R) – функция потенциальной энергии, которая, в соответствии с (19), имеет вид:
Как показано в [14, 21], температура Дебая определяется выражением:
(21)
$\Theta ({{k}_{n}},c) = {{A}_{w}}({{k}_{n}},c)\xi \left[ { - 1 + {{{\left( {1 + \frac{{8D}}{{{{k}_{{\text{B}}}}{{A}_{w}}({{k}_{n}},c){{\xi }^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right],$(22)
$\begin{gathered} {{A}_{w}}({{k}_{n}},c) = {{K}_{R}}\frac{{5{{k}_{n}}ab(b + 1)}}{{144(b - a)}}{{\left( {\frac{{{{r}_{{\text{o}}}}}}{c}} \right)}^{{b\, + \,2}}}, \\ {{K}_{R}} = \frac{{{{\hbar }^{2}}}}{{{{k}_{{\text{B}}}}r_{{\text{o}}}^{2}m}},\,\,\,\,\xi = \frac{9}{{{{k}_{n}}(\infty )}}, \\ \end{gathered} $Из (21) можно найти выражения для первого (γ), второго (q) и третьего (z) параметров Грюнайзена. Они имеют следующий вид:
(23)
$\begin{gathered} \gamma = - {{\left( {\frac{{\partial \ln \Theta }}{{\partial \ln {v}}}} \right)}_{T}} = \frac{{b + 2}}{{6(1 + {{X}_{w}})}}, \\ q = {{\left( {\frac{{\partial \ln \gamma }}{{\partial \ln {v}}}} \right)}_{T}} = \gamma \frac{{{{X}_{w}}(1 + 2{{X}_{w}})}}{{(1 + {{X}_{w}})}}, \\ z = - {{\left( {\frac{{\partial \ln q}}{{\partial \ln {v}}}} \right)}_{T}} = \gamma (1 + 4{{X}_{w}}) - 2q = \\ = \gamma \left( {\frac{{1 + 3{{X}_{w}}}}{{1 + {{X}_{w}}}}} \right) = \frac{{(b + 2)}}{6}\frac{{(1 + 3{{X}_{w}})}}{{{{{(1 + {{X}_{w}})}}^{2}}}}, \\ \end{gathered} $Используя (20)–(23), для уравнения состояния и изотермического модуля упругости (BT) можно получить следующие выражения [18, 22]:
(24)
$\begin{gathered} P = - {{\left( {\frac{{\partial {{f}_{H}}}}{{\partial {v}}}} \right)}_{T}} = \\ = \left[ {\frac{{{{k}_{n}}}}{6}DU{\kern 1pt} '(R) + 3{{k}_{{\text{B}}}}{{\Theta }_{{\text{E}}}}\gamma {{E}_{w}}\left( {\frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right)} \right]\frac{1}{{v}}, \\ \end{gathered} $В рамках RP-модели для удельной (на единицу площади) поверхностной энергии грани (100) нанокристалла, ее изохорной и изобарной производных по температуре и функции Δp можно получить следующие выражения [18, 22]:
(27)
$\sigma (N,f) = - \frac{{{{k}_{n}}(\infty )D{{R}^{2}}}}{{12{{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}r_{{\text{o}}}^{2}}}{{L}_{{\text{E}}}}(N,f),$(28)
$\begin{gathered} \sigma {\kern 1pt} '{{(T)}_{{v}}} = {{\left( {\frac{{\partial \sigma }}{{\partial T}}} \right)}_{{c,N,f}}} = \\ = - \frac{{3{{k}_{{\text{B}}}}{{R}^{2}}\gamma (N,f)}}{{2{{\alpha }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}(b + 2)r_{{\text{o}}}^{2}{{k}_{n}}(N,f){\text{*}}}}{{F}_{{\text{E}}}}\left( {\frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right), \\ \end{gathered} $(29)
$\begin{gathered} \sigma {\kern 1pt} '{{(T)}_{P}} = {{\left( {\frac{{\partial \sigma }}{{\partial T}}} \right)}_{{P,N,f}}} = \sigma {\kern 1pt} '{{(T)}_{{v}}} + {v}{{\alpha }_{p}}{{\left( {\frac{{\partial \sigma }}{{\partial {v}}}} \right)}_{{T,N,f}}} = \\ = \sigma {\kern 1pt} '{{(T)}_{{v}}} - \frac{2}{3}\sigma {{\alpha }_{p}}{{\Delta }_{p}}, \\ \end{gathered} $(30)
$\begin{gathered} {{\Delta }_{p}} = - \frac{1}{2}{{\left[ {\frac{{\partial \ln (\sigma )}}{{\partial \ln (c)}}} \right]}_{{T,N,{{k}_{p}},f}}} = 1 + \frac{1}{{2{{L}_{{\text{E}}}}(N,f)}} \times \\ \times \,\,\left\{ {U{\kern 1pt} '(R) - 9\left[ {q - \gamma {{t}_{y}}\left( {\frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right)} \right]{{H}_{w}}(N,T)} \right\}, \\ \end{gathered} $(31)
$\begin{gathered} {{C}_{{v}}} = 3N{{k}_{{\text{B}}}}{{F}_{{\text{E}}}}\left( {\frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right),\,\,\,\,{{\alpha }_{p}} = \frac{1}{{v}}{{\left( {\frac{{\partial {v}}}{{\partial T}}} \right)}_{P}} = \\ = \gamma \frac{{{{C}_{{v}}}}}{{V{{B}_{T}}}} = \frac{{\gamma {{C}_{{v}}}}}{{N{{B}_{T}}\left[ {{{\pi r_{{\text{o}}}^{3}} \mathord{\left/ {\vphantom {{\pi r_{{\text{o}}}^{3}} {(6{{k}_{p}})}}} \right. \kern-0em} {(6{{k}_{p}})}}} \right]}}\left( {\frac{{{{{v}}_{{\text{o}}}}}}{{v}}} \right), \\ {{L}_{{\text{E}}}}(N,f) = U(R) + 3{{H}_{w}}(N,T),\,\,\,\,{{{v}}_{{\text{o}}}} = \frac{{\pi r_{{\text{o}}}^{3}}}{{6k{}_{p}}}, \\ {{H}_{w}}(N,T) = \frac{{6\gamma (N,f)}}{{(b + 2)}}\left[ {\frac{{{{k}_{{\text{B}}}}{{\Theta }_{{\text{E}}}}(N,f)}}{{D{{k}_{n}}(N,f)}}} \right]{{E}_{w}}\left( {\frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right), \\ {{t}_{y}}(y) = 1 - \frac{{2y\exp (y)}}{{[\exp (2y) - 1]}}. \\ \end{gathered} $Отметим, что поверхностное давление также можно найти и из выражения (24), как разницу между давлениями, рассчитанными для макро- и нанокристалла:
Из полученных выражений (27)–(30) можно сделать следующие выводы:
1. Функция σ(P) с ростом давления увеличивается до максимума (при PM(N, f)), после чего она резко уменьшается и при определенном давлении (Pf(N, f)) переходит в отрицательную область. Более подробно это было изучено в [23].
2. При P < PM для веществ, у которых αp > 0 выполняется: σ'(T)P < σ'(T)v < 0. При T = 0 K обе функции при любых N–f-параметрах достигают максимума: σ'(0)P = σ'(0)v = 0 [18, 23]. Это согласуется с третьим началом термодинамики в “сильной” формулировке Планка. Таким образом, зависимости σ'(T)P и σ'(T)v нелинейные и полагать (как это сделано в [2, 7, 9, 10]), что σ'(T) = = const, не вполне корректно.
3. Функция Δp при P > PM переходит в отрицательную область, а при Pf она имеет разрыв второго рода. Подробнее это было изучено в [24].
4. Функции σ(N, f), σ'(T)P и σ'(T)v при P < PM убывают с уменьшением N тем заметнее, чем выше температура, или чем заметнее форма нанокристалла отклонена от энергетически оптимальной формы (для RP-модели это куб) [13, 14, 18, 23].
5. При высоких давлениях и низких температурах функция σ(N) может возрастать при изобарно-изотермическом уменьшении размера нанокристалла.
Таким образом, полученная в рамках RP-модели функция kn(N, f) вместе с формализмом из (20)–(31) позволяют рассчитать зависимость как уравнения состояния, так и всех решеточных и поверхностных свойств от размера и формы нанокристалла при любых (соответствующих твердой фазе) значениях температуры и удельного объема. Обобщение данной модели на случай наличия в системе вакансий и диффундирующих атомов было сделано в [19]. Это позволило в рамках RP(vac)-модели описать всю фазовую диаграмму простого вещества, включая фазовые переходы кристалл–жидкость, жидкость газ и кристалл–газ. В [19] было показано, что при уменьшении числа атомов в системе S-петля фазового перехода кристалл–жидкость на изотерме уравнения состояния уменьшается, а при определенном значении числа атомов (N0) S-петля кристалл–жидкость исчезает. При этом величина N0 увеличивается как с ростом температуры, так и при отклонении формы нано-системы от наиболее энергетически оптимальной (для RP(vac)-модели – это куб). В кластере из N < N0 атомов фазовый переход кристалл–жидкость исчезает. Для металлов была получена оценка: N0 = 50–300.
МЕТОД ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МЕЖАТОМНОГО ПОТЕНЦИАЛА
Для расчетов по формулам (20)–(31) необходимо определить параметры парного межатомного потенциала Ми–Леннард-Джонса (19). В литературе встречаются высказывания, что парный четырехпараметрический потенциал Ми–Леннард-Джонса (19) дает при расчетах решеточных свойств кристаллов худшие результаты, чем 3-х-параметрический потенциал Морзе для металлов, либо многочастичные потенциалы для Si или Ge (потенциалы типа Stillinger-Weber или Tersoff, которые включают не менее 10–12 параметров, и которые можно использовать только в численных расчетах). Это мнение возникло из-за трудностей определения самосогласованным образом всех четырех параметров потенциала Ми–Леннард-Джонса, особенно значений степенней a и b. Поэтому ранее (лет 50 тому назад) в большинстве расчетов брали ничем не обоснованные значения степенных параметров a = 6 и b = 12. Это было обусловлено тем, что с параметрами 6 и 12 в выражениях для U(R), U '(R) и U "(R) получаются квадратные уравнения, с которым было легче работать. Потенциал 6–12 использовался Джоном Эдвардом Леннард-Джонсом с соавторами (J.E. Lennard-Jones et al.) в “докомпьютерную эру” (т.е. в 30–40-х гг. XX в.) для описания свойств инертных газов [12]. По этой же причине потенциал 6–12 (названный в литературе потенциалом Леннард-Джонса) был применен для расчета свойств твердой фазы металлов и диэлектриков. Это привело к плохим результатам, на основе которых и сложилось неправильное мнение о неприменимости потенциала Ми–Леннард-Джонса общего вида (19), т.е. со степенями a–b, для описания свойств металлов. Отметим, что потенциал Морзе дает для металлов более лучшие результаты чем потенциал Леннард-Джонса 6–12. Это было обусловлено тем, что в “докомпьютерную эру” корректно определить три подгоночных параметра было намного легче, чем четыре. Но трехпараметрический потенциал Морзе является частным случаем четырехпараметрического потенциала Ми–Леннард-Джонса (19) при b = 2a [12].
Для определения параметров ro, D, b и a в [25] была предложена система четырех уравнений, в которые входили измеренные при Т = 0 K и P = 0 значения молярного объема (V00), молярной энергии сублимации (L00), температуры Дебая (Θ00) и первого параметра Грюнайзена (γ00). Это позволило в [25] рассчитать параметры потенциала (19) для многих кристаллов: для инертных газов, для металлов и для молекулярных кристаллов.
Но предложенный в [25] метод предполагает, что значения L00, Θ00 и γ00 определены в экспериментах при Т = 0 K и P = 0 с высокой точностью. К сожалению, этого не получается, причем наименее точно определяется величина γ00. Именно поэтому в [25] значения D, b и a были рассчитаны при фиксированных значениях L00 и Θ00 и различных величинах γ00, которые известны из литературы. При этом возникала неопределенность как в выборе величины γ00, так и в полученных при таком расчете наборе параметров b и a. Это привело к тому, что в работе [26] был предложен метод, в котором при данных значениях ro, D и b величина a корректировалась так, чтобы получалось хорошее совпадение с экспериментальным значением коэффициента теплового расширения αp при P = 0 и T = 300 K.
Но для тугоплавких металлов (Nb, Ta, Mo, W) с объемно-центрированной кубической (ОЦК) структурой такая корректировка величины a для получения хорошего согласия с величиной αp (P = 0, T = 300 K) оказалась недостаточной. Это было связано с тем, что для этих металлов приближенно измеряется не только значение γ00, но и величина Θ00. Например, для Mo и W в литературе приводятся следующие значения температуры Дебая:
Θ00(Mo)/K = 380 [20], 450 [27], 460–474.5 [28], 472.4–474.9 [29],259 ± 11 [30], 423 [31], 273.7 [32], 375–527 [33], 455–470 [34];
Θ00(W)/K = 310 [20], 400 [27], 382.58–390 [28], 382.6–384.6 [29], 384–388 [30], 383 [31], 232 [32], 378 ± 7 [35].
По этим причинам в [36, 37] при расчетах свойств ОЦК-W и кристалла Au с гранецентрированной кубической (ГЦК) структурой корректировались уже два параметра: b и a, при фиксированных значениях ro и D. Корректировка производилась до получения наилучшего совпадения как с экспериментальным значением коэффициента теплового расширения: αp (P = 0, T = 300 K), так и с экспериментальной зависимостью уравнения состояния P(300 K, v/vo). Однако, полученные таким путем параметры потенциала (19) привели к низким значениям модуля упругости BT (P = 0, T = 300 K). Поэтому в работах [38, 39] оптимизация потенциала (19) проводилась уже по трем параметрам: D, b и a, при фиксированном значении ro. В этом методе стремились получить наилучшее согласие с экспериментальными данными для αp(P = 0, T = 300 K), BT (P = 0, T = 300 K) и с экспериментальной зависимостью P(300 K, v/vo). Таким способом были получены параметры потенциала (19) для ОЦК-Mo [38] и ОЦК-Nb [39]. Эти параметры позволили получить хорошие зависимости для функций: P(T, v/vo), αp(P, T), BT(P, T), изохорной Cv и изобарной Cp = Сv(1 + + γαpT)) теплоемкости, температуры плавления Tm, а также производных этих функций по давлению. Однако, из-за высокого значения D рассчитанные значения энергии сублимации L00 и поверхностной энергии σ оказались много больше экспериментальных данных.
В связи с этим в данной работе предложена новая методика оптимизации потенциала (19) по двум параметрам: b и a, при фиксированных значениях ro и молярной энергии сублимации L00. Варьируя в широких диапазонах значения Θ00 и γ00: 100 < Θ00 < 600 и 1.1 < γ00 < 4.1, из рассчитанных по методу из [25] наборам параметров D, b и a отбираются только такие, которые при расчете уравнения состояния: P (300 K, v/vo = 0.8), модуля упругости: BT (P = 0, T = 300 K) и коэффициента теплового расширения: αp (P = 0, T = 300 K), дают величины, входящие в интервал допустимых значений.
В таблице 1 представлены полученные параметры межатомного потенциала (19) и вытекающие из этих параметров значения указанных свойств, как для ОЦК-Fe и ГЦК-Au, так и для тугоплавких ОЦК-металлов. Для ОЦК-Ta расчет параметров потенциала и свойств сделан для двух значений энергий сублимации: из [40] и из [41] из-за их заметного различия.
Таблица 1.
Энергия сублимации, параметры межатомного потенциала (19) и свойства, которые получаются при расчетах с использованием указанных параметров
| Кристалл | L00, кДж/моль |
ro [40], 10–10 м |
D/kB, K | b | a | P(0.8), ГПа |
αp 10–6 K– 1 |
BT = –v(∂P/∂v)T, ГПа |
B ′(P) = (∂BT/∂P)T | Θ, K | γ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe | 413.80 [40] | 2.4775 | 12 561.53 | 8.37 | 3.09 | 75.9 | 34.1 | 161.3 | 5.85 | 415.17 | 1.720 |
| Эксперимент | 50–60 [43] | 33–38 [45, 46] |
156–171 [46, 52] | 4–6 [46, 52] | 420–478 [14, 20] | 1.4–1.8 [14] | |||||
| Au | 368.19 [40] | 2.8751 | 7419.16 | 16.05 | 2.80 | 109.9 | 43.0 | 166.4 | 8.35 | 198.04 | 3.001 |
| Эксперимент | 65–75 [32] | 42–42.8 [45, 47] |
166.4–173.2 [27, 31] | 5.31 [32]–9.57 [47] | 156–178 [14] | 2.3–3.05 [14] | |||||
| Nb | 719.65 [40] | 2.8648 | 21 732.20 | 9.24 | 2.55 | 77.7 | 24.0 | 167.2 | 5.95 | 327.28 | 1.869 |
| Эксперимент | 50–60 [32] | 21.3–22.8 [45, 48, 49] |
144.2–170.2 [27, 31] | 3.3 [32]–14.5 [31] | 241 [30]–300 [27] | 1.3–1.69 [14] | |||||
| Ta | 706.26 [40] | 2.8648 | 21 318.49 | 7.86 | 3.49 | 86.3 | 18.5 | 192.8 | 5.80 | 289.93 | 1.640 |
| 785.608 [41] | – | 23 701.02 | 7.92 | 3.13 | 85.8 | 18.6 | 193.8 | 5.70 | 278.54 | 1.650 | |
| Эксперимент | 55–75 [32, 44] |
18–19.8 [45, 49, 50] |
192 [32]–195 [44]– 201.9 [31] |
3.4–3.55 [44]–3.842 [31] | 160.9 [32]–264.6 [29] | 1.5–2.19 [14] | |||||
| Mo | 655.31 [42] | 2.72 [25] | 19 832.34 | 8.29 | 3.93 | 115.0 | 16.4 | 248.7 | 6.09 | 451.13 | 1.710 |
| Эксперимент | 80–95 [32, 34] |
14–16.5 [45, 49, 51] |
244–260 [34] | 4.21–4.67 [34] | 455–470 [34] | 1.95–2.03 [34] | |||||
| W | 848.10 [40] | 2.7365 | 25 594.79 | 8.82 | 3.45 | 136.2 | 15.0 | 295.7 | 6.10612 | 330.35 | 1.800 |
| Эксперимент | 103–120 [32] | 11–15 [35, 45, 49] |
296 [32]–323.3 [27] | 4.4 [32]–19.1 [31] | 232 [32]–400 [27] 310–610 [14] |
1.1–1.76 [14] | |||||
Как видно из табл. 1, полученные нами величины P(300 K, v/vo = 0.8) получились несколько выше экспериментальных данных. Это указывает на то, что рассчитанные параметры потенциала работоспособны в области упругих деформаций, т.е. при v/vo ≥ 0.9. Но рассчитанные предлагаемым методам потенциальные параметры дают в комплексе лучшее согласие с набором экспериментальных данных, чем параметры потенциала (19) из [25, 26, 36–40]. Для ОЦК-Ta лучшее согласие рассчитанных свойств с экспериментальными данными получено из значения энергии сублимации, которое приведено в [41].
Помимо определения параметров потенциала (19) данный метод расчета позволяет определить более достоверные значения для Θ, γ и L00. Как было указано в [21, 53] современные экспериментальные методы не позволяют измерить данные параметры с необходимой точностью (на это указывает разброс экспериментальных данных в табл. 1). Поэтому использование данного метода весьма актуально.
6. РЕЗУЛЬТАТЫ РАСЧЕТА ПОВЕРХНОСТНЫХ СВОЙСТВ МАКРОКРИСТАЛЛА
В таблице 2 представлены рассчитанные при использовании параметров потенциала (19) из табл. 1 значения: v/vo, σ, σ'(T)v и σ'(T)P (в 10–6 Дж/(м2 · K)), σ'(P)T = (∂σ/∂P)T – изотермическая производная σ по P (в 10–3 Дж/(м2 · ГПа)) и Δp из (30). Значение σ'(P)T рассчитывалось путем численного дифференцирования функции σ по давлению вдоль изотермы.
Таблица 2.
Значения поверхностных свойств рассчитанные для макрокристалла при P = 0*
| Элемент | T, K | v/vo | σ(100), 10–3 Дж/м2 |
–σ′(T)v, мкДж/(м2 · K) |
–σ′(T)P, мкДж/(м2 · K) |
σ′(P)T, мДж/(м2 · ГПа) |
Δp |
|---|---|---|---|---|---|---|---|
| Fe | 300 | 1.01199 | 2202.98 | 60.48 | 112.94 | 9.53 | 1.0468 |
| 1000 | 1.03953 | 2115.60 | 64.49 | 131.87 | 11.59 | 1.1596 | |
| Эксперимент | 2420–2480 [1, 4] (2220–2920) [1] (2500) [5] 1910 ± 190 [54] 2040 [55] |
||||||
| Au | 300 | 1.01302 | 1531.38 | 50.98 | 98.93 | 6.70 | 1.0923 |
| 1000 | 1.04803 | 1454.77 | 50.80 | 120.53 | 9.89 | 1.3159 | |
| Эксперимент | 1500–1510 [1] (1630‒1800) [1] 1510 ± 160 [8] 1410 ± 37 [54] 1363 [55] |
500 [55] 100‒105 [56] |
|||||
| Nb | 300 | 1.00794 | 2870.66 | 47.02 | 94.32 | 11.78 | 1.0292 |
| 2500 | 1.07336 | 2632.27 | 47.64 | 119.81 | 18.11 | 1.2547 | |
| Эксперимент | 2660–2700 [1] (2860‒2990) [1] 2210 ± 54 [54] 2150 [55] |
170 [55] | |||||
| Ta | 300 | 1.00601 | 2819.56 | 47.66 | 83.39 | 10.00 | 1.0262 |
| 2500 | 1.05367 | 2617.67 | 48.25 | 97.88 | 13.93 | 1.2275 | |
| 300 | 1.00601 | 3136.47 | 47.83 | 87.66 | 11.04 | 1.0237 | |
| 2500 | 1.05361 | 2924.95 | 48.26 | 102.47 | 15.12 | 1.2049 | |
| Эксперимент | 2900–3150 [1] (3100‒4050) [1] 2480 ± 70 [54] 2414 [55] |
170 [55] | |||||
| Mo | 300 | 1.00601 | 2907.50 | 49.66 | 82.48 | 8.02 | 1.0294 |
| 2500 | 1.05069 | 2696.50 | 53.52 | 103.01 | 11.3975 | 1.2557 | |
| Эксперимент | 2910–3000 [1] (3810‒3840) [1] (3180) [5] 2630 ± 50 [54] 2582 [55] |
180 [55] | |||||
| W | 300 | 1.00499 | 3715.79 | 51.60 | 89.72 | 8.58 | 1.0238 |
| 2500 | 1.04352 | 3497.01 | 53.21 | 105.576 | 11.57 | 1.2062 | |
| Эксперимент | 3270–3680 [1] (3900‒4640) [1] 2210 ± 22 [54] 2653 [55] |
170 [55] | |||||
* Для каждого кристалла в первой строке представлены расчеты при T = 300 K, во второй: при T = 1000 K для ОЦК-Fe и ГЦК-Au, и при T = 2500 K для ОЦК металлов Nb, Ta, Mo, W. В третьей строке представлены известные из литературы экспериментальные и теоретические (в скобках) данные. Для ОЦК-Ta расчеты сделаны для двух наборов потенциала из табл. 1.
Так как для нанокристаллов экспериментальных данных в литературе нет, то для проверки метода расчеты были проведены для макрокристаллов (N = ∞) при P = 0 и двух значениях температуры. Для каждого кристалла в первой строке представлены расчеты при T = 300 K, во второй: при T = 1000 K для ОЦК-Fe и ГЦК-Au, и при T = = 2500 K для тугоплавких ОЦК металлов: Nb, Ta, Mo, W. В третьей строке представлены известные из работ [1, 4, 5, 54–56] экспериментальные и теоретические (в скобках) данные.
Для ОЦК-Ta расчет был проведен для двух наборов параметров потенциала (19), которые представлены в табл. 1: в первых двух строках для первого набора, в третьей и четвертой – для второго набора параметров.
Наиболее хорошо поверхностные свойства экспериментально изучены для макрокристаллов ОЦК-Fe и ГЦК-Au. При этом экспериментальные значения σ и σ'(T)P оценивались при T $ \gg $ Θ, а теоретические значения σ – при T = 0 K. Как видно из табл. 2 наши расчеты σ(100) хорошо согласуются с экспериментальными оценками из [1, 4. 8, 54, 55]. Что касается производных σ по T и P, то в литературе имеется очень мало данных для σ'(T)P, а для σ'(T)v, σ'(P) и Δp никаких данных (ни теоретических, ни экспериментальных) в литературе нет.
В работах [4, 6, 7, 54, 55] точность экспериментального определения величины σ(100) для металлов оценивают в пределах ±(100–200) × 10–3 Дж/м2. Численные методы расчета σ(100), согласно [6, 8], имеют точность ±(180–640) × 10–3 Дж/м2. В связи с этим определить значение σ'(T)P, которое по величине порядка 10–(4–5) Дж/м2, экспериментально, либо путем численного моделирования очень проблематично. Исходя из этого, можно утверждать, что полученные здесь величины σ′(T)v являются более корректными, чем известные из литературы экспериментальные оценки.
ИЗМЕНЕНИЕ ПОВЕРХНОСТНЫХ СВОЙСТВ ПРИ ПЕРЕХОДЕ ОТ МАКРО- К НАНОКРИСТАЛЛУ ДЛЯ ОЦК-ТАНТАЛА
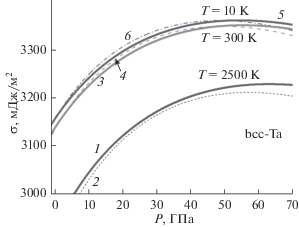
Из представленных в табл. 1 и 2 металлов наименее изучен ОЦК-тантал (m(Ta) = 180.948 а. е. м, $k_{n}^{{\text{o}}}(\infty )$ = 8, kp = 0.6802, α = π/(6kp) = 0.7698), который имеет высокую температуру плавления: Tm(P = 0) = 3295 K [30], 3293 K [49], 3290 K [50]. Поэтому нами были рассчитаны поверхностные свойства как макро-, так и нано-Ta при различных P–T–N-условиях. На рис. 1–3 представлены барические зависимости поверхностных свойств для ОЦК-Ta, атомы которого взаимодействуют посредством потенциала (19) с параметрами из табл. 1: набор со степенями 3.13–7.92. Расчеты выполнены вдоль трех изотерм (T = 10, 300, 2500 K) как для макрокристалла, так и для нанокристалла кубической формы (f = 1) при Npo = 7, т.е. состоящего из N = INT$\left[ {{{fN_{{po}}^{{\text{3}}}} \mathord{\left/ {\vphantom {{fN_{{po}}^{{\text{3}}}} \alpha }} \right. \kern-0em} \alpha }} \right]$ = 446 атомов. Толстыми сплошными линиями 1, 3, 5 показаны зависимости для макрокристалла, а тонкими линиями 2, 4, 6 – для нанокристалла при температурах T = = 2500, 300, 10 K соответственно.
Рис. 2.
Изменение изохорной (4 верхние спадающие линии) и изобарной (4 нижние возрастающие кривые) производных удельной поверхностной энергии по температуре для ОЦК-Ta с ростом давления.
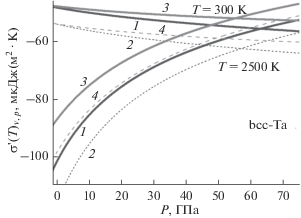
Рис. 3.
Барические зависимости производной по давлению удельной поверхностной энергии грани (100) ОЦК-Ta вдоль разных изотерм.
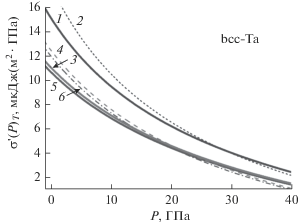
На рис. 1 показана барическая зависимость удельной поверхностной энергии (в 10–3 Дж/м2) грани (100) ОЦК-Ta. Как видно из полученных зависимостей σ(P), при P = 0 величина σ уменьшается c уменьшением N тем заметнее, чем выше температура. Но при низких температурах и высоких давлениях на изотерме имеются две P-точки, в которых зависимости σ(P) для макро- и нанокристаллов пересекаются. Поэтому в P-точке удельная поверхностная энергия не зависит от размера нанокристалла: σ(N) = σ(∞). Впервые такие P-точки были обнаружены в [57] при изучении свойств ОЦК-Fe. Потом параметры P-точек были изучены для нанокристаллов ОЦК-W в [36] и для ОЦК-Nb в [58]. С ростом температуры эти P-точки сближаются, и при высоких температурах P-точек на изотерме уже нет. В области, оконтуренной P-точками, величина σ возрастает при изотермо-изобарическом уменьшении размера нанокристалла. Такое поведение функции σ(P, N) обусловлено тем, что при низких температура и высоких давлениях поверхностное давление сжимает нанокристалл, что и приводит к появлению первой P-точки, и к неравенству σ(N) > σ(∞). С ростом давления функция σ для нанокристалла уменьшается заметнее, чем для макрокристалла, что и приводит к образованию второй P-точки на изотерме. С ростом температуры поверхностное давление уменьшается, что и приводит к исчезновению области с P-точками.
На рис. 2 показаны барические зависимости для σ'(T)v – изохорной (4 верхние спадающие линии) и σ'(T)P – изобарной (4 нижние возрастающие кривые) производных удельной поверхностной энергии по температуре (в 10–6 Дж/(м2 · K)) для ОЦК-Ta. Как видно из рис. 2, при низких давлениях выполняется |σ'(T)v| < |σ'(T)P|. При P = 0 и T $ \gg $ Θ величина σ'(T)v практически не зависит от температуры.
На рис. 3 показаны барические зависимости для σ'(P)T – производной по давлению удельной поверхностной энергии (в 10–3 Дж/(м2 · ГПа)) ОЦК-Ta вдоль изотерм: 2500 K (линии 1 и 2), 300 K (линии 3 и 4) и 10 K (линии 5 и 6). Из рис. 3 следует, что в области низких давлений величина σ'(P)T увеличивается при изотермо-изобарическом уменьшении N. Но с ростом давления картина меняется на противоположную. Таким образом, для определенной температуры существует определенное давление, где величина σ'(P)T не зависит от размера кристалла.
ЗАКЛЮЧЕНИЕ
Предложен метод для расчета удельной поверхностной энергии, изохорной и изобарной производных функции σ по температуре, и изотермической производной функции σ по давлению. Показано, что метод применим как для макро-, так и для нанокристалла однокомпонентного вещества с заданным числом атомов и с определенной формой поверхности.
Разработан метод самосогласованного определения параметров парного межатомного потенциала Ми–Леннард-Джонса исходящий из экспериментальных данных по термоупругим свойствам кристалла. Данным методом были определены параметры межатомного потенциала для Fe, Au, Nb, Ta, Mo, W. Показано, что при использовании этих параметров в аналитических расчетах получаются более надежные результаты, чем при использовании параметров потенциала из других работ.
Показано, что рассчитанные значения удельной поверхностной энергии и изобарной производной функции σ по температуре хорошо согласуются с экспериментальными оценками известными из литературы. Впервые рассчитаны значения изохорной производной функции σ по температуре, изотермической производной функции σ по давлению и величины Δp при P = 0 и различных температурах для макрокристаллов Fe, Au, Nb, Ta, Mo, W.
На примере ОЦК-Ta изучены изменения поверхностных свойств при уменьшении размера нанокристалла вдоль изотерм T = 10, 300, 2500 K. Показано, что имеются оконтуренные P-точками P–T-области, в которых функция σ возрастает при изоморфо-изотермо-изобарическом уменьшении размера нанокристалла.
Список литературы
Jiang Q., Lu H.M., Zhao M. // J. Phys.: Cond. Matt. 2004. V. 16. № 4. P. 521.https://doi.org/10.1088/0953-8984/16/4/001
Zhao M., Zheng W., Li J., Wen Z., Gu M., Sun C.Q. // Phys. Rev. B. 2007. V. 75. № 8. P. 085427.https://doi.org/10.1103/PhysRevB.75.085427
Aqra F., Ayyad A. // Appl. Surf. Sci. 2011. V. 257. № 15. P. 6372.https://doi.org/10.1016/j.apsusc.2011.01.123
Schönecker S., Li X., Johansson B., Kwon S.K., Vitos L. // Scient. Rep. 2015. V. 5. P. 14 860.https://doi.org/10.1038/srep14860
Tran R., Xu Z., Radhakrishnan B., Winston D., Sun W., Persson K.A., Ong S.P. // Scient. Data. 2016. V. 3. № 1. P. 1.https://doi.org/10.1038/sdata.2016.80
De Waele S., Lejaeghere K., Sluydts M., Cottenier S. // Phys. Rev. B. 2016. V. 94. № 23. P. 235 418.https://doi.org/10.1103/PhysRevB.94.235418
Cheng T., Fang D., Yang Y. // Appl. Surf. Sci. 2017. V. 393. P. 364.https://doi.org/10.1016/j.apsusc.2016.09.147
Patra A., Bates J.E., Sun J., Perdew J.P. // Proc. Nat. Acad. Sci. 2017. V. 114. № 44. P. E9188.https://doi.org/10.1073/pnas.1713320114
Zhang X., Li W., Kou H., Shao J., Deng Y., Zhang X., Ma J., Li Y., Zhang X. // J. Appl. Phys. 2019. V. 125. № 18. P. 185 105.https://doi.org/10.1063/1.5090301
Шебзухова И.Г., Арефьева Л.П. // ЖТФ. 2019. Т. 89. № 2. С. 306.https://doi.org/10.1134/S1063784219020208
Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Часть 1. М.: Изд-во Наука, 1976. 584 с.
Мелвин-Хьюз Э.А. Физическая химия. В 2-х томах. Москва: Изд-во Иностранной Литературы, 1962. 1148 с.
Магомедов М.Н. // ФТТ. 2004. Т. 46. № 5. С. 924.https://doi.org/10.1134/1.1744976
Магомедов М.Н. Изучение межатомного взаимодействия, образования вакансий и самодиффузии в кристаллах. М.: Изд-во Физматлит, 2010. 544 с.
Магомедов М.Н. // Российские нанотехнологии. 2014. Т. 9. № 5–6. С. 63.https://doi.org/10.1134/S1995078014030100
Магомедов М.Н. // ЖТФ. 2013. Т. 83. № 6. С. 155.https://doi.org/10.1134/S1063784213060212
Нагаев Э.Л. // УФН. 1992. Т. 162. № 9. С. 49.https://doi.org/10.3367/UFNr.0162.199209b.0049
Магомедов М.Н. // Кристаллография. 2017. Т. 62. № 3. С. 487.https://doi.org/10.1134/S1063774517030142
Магомедов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2019. № 9. С. 103.https://doi.org/10.1134/S1027451019050070
Жирифалько Л. Статистическая физика твердого тела. М.: Изд-во Мир, 1975. 383 с.
Магомедов М.Н. // ЖТФ. 2013. Т. 83. № 9. С. 56.https://doi.org/10.1134/S106378421309020X
Магомедов М.Н. // Российские нанотехнологии. 2019. Т. 14. № 1–2. С. 19.https://doi.org/10.1134/S1995078019010063
Магомедов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2013. № 11. С. 107.https://doi.org/10.1134/S1027451013060104
Магомедов М.Н. // ЖТФ. 2016. Т. 86. № 5. С. 84.https://doi.org/10.1134/S1063784216050145
Магомедов М.Н. // ТВТ. 2006. Т. 44. № 4. С. 518.https://doi.org/10.1007/s10740-006-0064-5
Магомедов М.Н. // ЖТФ. 2015. Т. 85. № 11. С. 48.https://doi.org/10.1134/S1063784215110195
Киттель Ч. Введение в физику твердого тела. М.: Изд-во Наука, 1978. 792 с.
Shukla M.M., Padial N.T. // Revista Brasileira de Física. 1973. V. 3. № 1. P. 39. http://sbfisica.org.br/ bjp/download/v03/v03a03.pdf.
Verma J.K.D., Aggarwal M.D. // J. Appl. Phys. 1975. V. 46. № 7. P. 2841.https://doi.org/10.1063/1.322028
Зиновьев В.Е. Теплофизические свойства металлов при высоких температурах. Справочник. М.: Изд-во Металлургия, 1989. 384 с.
Физические величины: Справочник / Под. ред. Григорьева И.С., Мейлихова Е.3. М.: Изд-во Энергоатомиздат, 1991. 1232 с.
Karbasi A., Saxena S.K., Hrubiak R. // CALPHAD. 2011. V. 35. № 1. P. 72.https://doi.org/10.1016/j.calphad.2010.11.007
Desai P.D. // J. Phys. Chem. Ref. Data. 1987. V. 16. № 1. P. 91.https://doi.org/10.1063/1.555794
Huang X., Li F., Zhou Q., Meng Y., Litasov K.D., Wang X., Liu B., Cui T. // Scient. Rep. 2016. V. 6. P. 19 923.https://doi.org/10.1038/srep19923
Бодряков В.Ю. // ТВТ. 2015. Т. 53. № 5. С. 676.https://doi.org/10.1134/S0018151X15040069
Gazanova N.Sh. // Appl. Sol. St. Chem. 2018. № 3(4). P. 36. https://doi.org/10.18572/2619-0141-2018-3-4-36-40
Ahmedov E.N. // J. Phys.: Conf. Ser. 2019. V. 1348. № 012002. P. 1.https://doi.org/10.1088/1742-6596/1348/1/012002
Akhmedov E.N. // J. Phys. Chem. Sol. 2018. V. 121. P. 62.https://doi.org/10.1016/j.jpcs.2018.05.011
Kraminin S.P., Ahmedov E.N. // J. Phys. Chem. Sol. 2019. V. 135. P. 109108.https://doi.org/10.1016/j.jpcs.2019.109108
Zhen Shu, Davies G.J. // Phys. Stat. Solidi (a). 1983. V. 78. № 2. P. 595.https://doi.org/10.1002/pssa.2210780226
Электронная база данных: http://www.chem.msu.su/ cgi-bin/tkv.pl
Термические константы веществ. Справочник в 10-ти выпусках / Под ред. Глушко В.П. М.: Изд-во ВИНИТИ. 1965–1982.
Белащенко Д.К., Островский О.И. // Журн. физ. химии. 2011. Т. 85. № 6. С. 1063.https://doi.org/10.1134/S0036024411060094
Gu J.-B., Wang C.-J., Zhang W.-X., Sun B., Liu G.-Q., Liu D.-D., Yang X.-D. // Chinese Phys. B. 2016. V. 25. № 12. P. 126103.https://doi.org/10.1088/1674-1056/25/12/126103
Новикова С.И. Тепловое расширение твердых тел. М.: Изд-во Наука, 1974. 294 с.
Wilburn D.R., Bassett W.A. // American Mineralogist. 1978. V. 63. № 5-6. P. 591. https://pubs.geoscienceworld.org/msa/ammin/article-abstract/63/5-6/591/40926
Pamato M.G., Wood I.G., Dobson D.P., Hunt S.A., Vočadlo L. // J. Appl. Crystallography. 2018. V. 51. № 2. P. 470.https://doi.org/10.1107/S1600576718002248
Straumanis M.E., Zyszczynski S. // J. Applied Crystallography. 1970. V. 3. № 1. P. 1.https://doi.org/10.1107/s002188987000554x
Wang K., Reeber R.R. // Mater. Scien. Eng.: R, 1998. V. 23. № 3. P. 101.https://doi.org/10.1016/s0927-796x(98)00011-4
Бодряков В.Ю. // ТВТ. 2016. Т. 54. № 3. С. 336.https://doi.org/10.1134/S0018151X16030020
Бодряков В.Ю. // ТВТ. 2014. Т. 52. № 6. С. 863.https://doi.org/10.1134/S0018151X14040051
Shibazaki Y., Nishida K., Higo Y., Igarashi M., Tahara M., Sakamaki T., Terasaki H., Shimoyama Y., Kuwabara S., Takubo Y., Ohtani E. // American Mineralogist. 2016. 101. № 5. P. 1150.https://doi.org/10.2138/am-2016-5545
Магомедов М.Н. // ЖТФ. 2010. Т. 80. № 9. С. 150.https://doi.org/10.1134/S1063784210090240
Kumikov V.K., Khokonov Kh.B. // J. Appl. Phys. 1983. V. 54. № 3. P. 1346.https://doi.org/10.1063/1.332209
Alchagirov B.B., Taova T.M., Khokonov Kh.B. // Transactions of JWRI (Japan). 2001. V. 30. P. 287. https://repository.exst.jaxa.jp/dspace/handle/a-is/48071
Задумкин С.Н. // Докл. АН СССР. 1955. Т. 101. № 3. С. 507.
Магомедов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2018. № 2. С. 103.https://doi.org/10.1134/S1027451018010299
Kramynin S.P. // J. Phys. Chem. Sol. 2020. V. 143. P. 109 464.https://doi.org/10.1016/j.jpcs.2020.109464
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования