1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 3, 2020

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 3, стр. 32-36

Описание статистического разброса энергии ионов после прохождения тонкой мишени

Н. В. Новиков a, *, Я. А. Теплова a, **

a Московский государственный университет им. М.В. Ломоносова, НИИЯФ им. Д.В. Скобельцына
119991 Москва, Россия

* E-mail: nvnovikov65@mail.ru
** E-mail: sonatina1929@mail.ru

Поступила в редакцию 16.07.2019
После доработки 18.08.2019
Принята к публикации 20.08.2019

Полный текст (PDF)

Аннотация

Статистический разброс потери энергии быстрых ионов моделируется методом Монте-Карло в случае больших и малых переданных импульсов. Область применимости приближения Бора определена для часто используемых твердых мишеней. Асимметрия в распределении потери энергии ионов связана с влиянием больших переданных импульсов и наблюдается в широком диапазоне значений энергии ионов и толщины мишени.

Ключевые слова: потери энергии, средняя энергия ионов, статистический разброс потери энергии, распределение Ландау–Вавилова, метод Монте-Карло.

ВВЕДЕНИЕ

Потери энергии ионов при прохождении через вещество и отражении от поверхности изучают теоретически и экспериментально в широком диапазоне значений энергии ионов E0 [1]. Распределение по энергии ионов после прохождения мишени толщиной x можно описать функцией Гаусса с параметрами: средняя энергия E и стандартное отклонение Ω. Разброс в значениях энергии иона E ± Ω объясняется статистическим характером столкновения для разных прицельных параметров, оболочечной структурой атомов среды, изменением эффективного заряда иона и неоднородностью плотности материала твердой мишени. Значение Ω важно при исследовании распределений ионов по глубине мишени, в методе резерфордовского обратного рассеяния и при оценке воздействия иона на материал мишени.

Первую теоретическую модель для описания статистического разброса потери энергии предложил Бор [2] на основе сечения рассеяния Резерфорда. Статистический разброс потери энергии ионов в этой модели обусловлен большим количеством столкновений иона со свободными электронами. При больших прицельных параметрах в каждом из столкновений ион теряет малую часть своей энергии. В этом случае распределение по энергии f(E ') ионов, прошедших через мишень, нормировано:

(1)
$\int\limits_0^{{{E}_{0}}} {dE{\kern 1pt} 'f(E{\kern 1pt} ') = 1} $
и описывается функцией Гаусса fG(E ') cо средней величиной потери энергии
(2)
$E = \int\limits_0^{{{E}_{0}}} {dE{\kern 1pt} 'E{\kern 1pt} '{{f}_{{\text{G}}}}(E{\kern 1pt} ')} $
и квадратом стандартного отклонения:
$\Omega _{{\text{B}}}^{2} = 4\pi {{Z}^{2}}{{Z}_{t}}\rho x,$
где Z – заряд ядра иона, Zt – заряд ядра атома мишени, ρ – плотность мишени.

Модель Бора использует несколько приближений: до взаимодействия с мишенью разброса в распределении по энергии иона нет (Ω → 0 при x → 0); разброс потери энергии иона в одном столкновении со свободным электроном связан с небольшой величиной переданного импульса (малые углы рассеяния) и описывается нормальным распределением; при прохождении через тонкий слой мишени толщиной x $ \ll $ R(E0), где R(E0) – пробег иона с энергией E0, ионы теряют небольшую часть своей энергии – E $ \ll $ E0; скорость иона V значительно превышает скорости электронов в газе свободных электронов $V \gg {{V}_{0}}{{Z}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},$ и параметр $\Omega _{{\text{B}}}^{2}$ не зависит от E0; при прохождении через мишень толщиной x заряд ионов q ≤ Z не меняется, а параметр $\Omega _{{\text{B}}}^{2}$ не зависит от q; мишень бесструктурная (аморфная или поликристаллическая) и однородная.

Уточнение модели проведено на основе принципов квантовой механики рядом авторов. Линдхард и Шарф [3], используя формализм функции диэлектрической проницаемости, расширили диапазон использования модели Бора на область промежуточных и медленных столкновений и ввели параметр приведенного разброса потерь энергии ${{{{\Omega }^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{\Omega }^{{\text{2}}}}} {\Omega _{{\text{B}}}^{{\text{2}}}}}} \right. \kern-0em} {\Omega _{{\text{B}}}^{{\text{2}}}}},$ величина которого зависит от E0. Эта поправка важна для ионов в диапазоне значений энергии, в котором неупругие потери энергии достигают максимума. Далее были учтены вклады разных оболочек атома мишени в распределение электронной плотности [4, 5] и использовано приближение эффективного заряда иона [6] для описания потери энергии ионов с зарядами q < Z [7]. Результаты расчетов в такой модели согласуются с экспериментальными данными с точностью до ~5% [8], а в пределе быстрых столкновений совпадают с оценкой для газа свободных электронов (${{{{\Omega }^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{\Omega }^{{\text{2}}}}} {\Omega _{{\text{B}}}^{{\text{2}}}}}} \right. \kern-0em} {\Omega _{{\text{B}}}^{{\text{2}}}}} \to 1$). Уточнение электронной плотности и заряда иона в области промежуточных и медленных столкновений позволило получить эмпирическое соотношение, которое описывает изменение ${{{{\Omega }^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{\Omega }^{{\text{2}}}}} {\Omega _{{\text{B}}}^{{\text{2}}}}}} \right. \kern-0em} {\Omega _{{\text{B}}}^{{\text{2}}}}}$ при уменьшении энергии иона [8]. Так как мишень однородная, а сечение ионизации и эффективный заряд иона не зависят от x, стандартное отклонение в разбросе потери энергии Ω2, как и в модели Бора, линейно возрастает с увеличением толщины мишени (Ω2 ~ x).

Из-за статистической природы потери энергии в одном столкновении могут возникать флуктуации, когда при малых прицельных параметрах один из электронов атома (δ-электрон) получает большой переданный импульс. Это приводит к тому, что распределение по потерям энергии в тонкой мишени (x ≤ 1 мкм) представляется в виде нескольких максимумов разной амплитуды [9], которые для мишени толщиной x ≥ 1 мкм объединяются в один несимметричный максимум. Распределение по энергии ионов с учетом больших переданных импульсов в одном столкновении fLV(E ') получило название распределения Ландау–Вавилова [10, 11]. Эта модель качественно описывает экспериментальные распределения потери энергии быстрых ионов после прохождения мишени толщиной x ≥ 10 мкм. Погрешность аппроксимации асимметричного распределения fLV(E ') функцией Гаусса fG(E ') зависит от заряда ядра иона Z, энергии E0 и толщины мишени x.

Цель работы – выяснить границы применимости приближения Бора для описания статистического разброса потери энергии быстрых ионов в часто используемых твердых мишенях (графит, кремний, медь и серебро) и исследовать соотношение между результатами аппроксимации распределения по энергии быстрых ионов с помощью функций Гаусса и Ландау–Вавилова.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Расчеты распределения ионов, прошедших через твердую мишень, были выполнены методом Монте-Карло с помощью нескольких программ. Моделирование статистического разброса потери энергии в программе SRIM [12] основано на уточненной модели Бора, в которой распределение по энергии ионов описывается функцией Гаусса fG(E ') в широком диапазоне толщины мишени 1 нм ≤ x ≤ R(E0) и значений энергии иона 1 кэВ ≤ ≤ E0 ≤ 10 ГэВ.

В соответствии с моделью Бора (3) статистический разброс потери энергии быстрых ионов (E0 ≥ ≥ 0.5 МэВ/нуклон) в тонкой мишени (x ≤ 1 мкм) не зависит от E0 и возрастает с увеличением толщины мишени как Ω ~ ${{\sqrt x }^{{}}}$ (рис. 1а). В случае толщины мишени, близкой к пробегу иона, статистический разброс потери энергии уменьшается с увеличением x (рис. 1б), а модель Бора требует уточнения. Эта особенность связана с нарушением приближения тонкой мишени и уменьшением средней потери энергии иона при x ~ R(E0). Диапазон толщины мишени x ≤ xmax(E0), когда выполняется соотношение (3), зависит от энергии иона E0. В углеродной мишени xmax = 2.5 мкм для E0 = 0.5 МэВ/нуклон, xmax = 5 мкм для E0 = = 1 МэВ/нуклон, xmax = 1 мкм для E0 = 2 МэВ/нуклон. В области значений энергии E0 < < 0.5 МэВ/нуклон для оценки статистического разброса потери энергии ионов можно использовать приведенный параметр ${{{{\Omega }^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{\Omega }^{{\text{2}}}}} {\Omega _{{\text{B}}}^{{\text{2}}}}}} \right. \kern-0em} {\Omega _{{\text{B}}}^{{\text{2}}}}}$ [8].

Рис. 1.

Зависимость статистического разброса потери энергии ионов аргона в углероде от толщины мишени при энергии ионов: 0.5 (o); 1 (Δ); 2 МэВ/нуклон (+). Сплошной линией обозначена зависимость статистического разброса в виде Ω ~ $\sqrt x .$

Линейная аппроксимация зависимости статистического разброса потери энергии от Z для ионов в диапазоне E0 ≥ 0.5 МэВ/нуклон (рис. 2) позволяет вычислить параметр A(Zt):

(4)
$\Omega _{{\text{B}}}^{{}} = A({{Z}_{t}})Z\sqrt x ,$
который равен статистическому разбросу потери энергии быстрых ионов после прохождения мишени толщиной x ≤ 1 мкм. Результаты расчетов этого параметра для часто используемых твердых мишеней приводятся в табл. 1. В соответствии с приближением Бора A(Zt) возрастает с увеличением Zt.

Рис. 2.

Зависимость статистического разброса потери энергии ионов c энергией E ≥ 0.5 МэВ/нуклон после прохождения мишени толщиной x = 1 мкм при заряде ядра атома мишени: 6 (1); 14 (2); 29 (3); 47 (4).

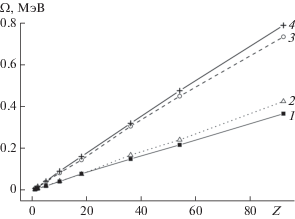
Таблица 1.  

Значения коэффициента A (4) для часто используемых аморфных мишеней при аппроксимации статистического разброса потери энергии ионов c произвольным зарядом ядра Z и энергией E ≥ 0.5 МэВ/нуклон

Zt A, кэВ/мкм1/2
  6 3.98 ± 0.04
14 4.62 ± 0.04
29 8.06 ± 0.10
47 8.61 ± 0.07

Распределение Ландау–Вавилова, которое используется при моделировании потери энергии быстрых ионов с помощью программ GEANT4 [13] и FLUKA [14], качественно описывает экспериментальные данные для быстрых протонов (рис. 3). Экспериментальное и вычисленное распределения имеют асимметрию. Медленное уменьшение количества ионов при увеличении потери энергии в результатах моделирования связано с вкладом больших переданных импульсов и образованием δ-электронов. Для количественной характеристики отличия распределения $f(E{\kern 1pt} ')$ от функции Гаусса ${{f}_{{\text{G}}}}(E{\kern 1pt} ')$ можно использовать интеграл

(5)
$F = \int\limits_{{{E}_{1}}}^{{{E}_{2}}} {dE{\kern 1pt} '} [f(E{\kern 1pt} ') - {{f}_{{\text{G}}}}(E{\kern 1pt} ')]$
по области энергии E1 ≤ E ≤ E2, в которой f(E ') ≥ ≥ fG(E '). Из экспериментального распределения (рис. 3) получаем, что E1 = 8.7 кэВ, E2 = 13 кэВ и Fex ≈ 0.163. Параметр (5) можно применить также к распределению Ландау–Вавилова fLV(E '). Результаты расчетов распределения быстрых ионов по программе GEANT4 показали, что в диапазоне значений энергии протона 5 МэВ ≤ E0 ≤ 5 ГэВ и толщины мишени из кремния x > 1 мкм распределение fLV(E ') отличается от fG(E ') более чем на 12% (FLV > 0.12). Из-за асимметрии функции fLV(E ') энергия иона Emax, при которой потери энергии в распределении Ландау–Вавилова достигают максимальной величины $f_{{{\text{LV}}}}^{{\max }} = {{f}_{{{\text{LV}}}}}(E_{{\max }}^{{}}),$ отличается от среднего значения E (2). По сравнению с распределением Гаусса максимум в распределении Ландау–Вавилова возрастает до $f_{{{\text{LV}}}}^{{\max }} > {{f}_{{\text{G}}}}(E),$ а ширина на половине высоты уменьшается (рис. 3). Такое перераспределение ионов по энергии приводит к тому, что в области энергии E ' ≈ E функция Гаусса дает завышенную оценку количества ионов fG(E ') > fLV(E '), а в областях E ' ≤ Emax и E ' $ \gg $ E соотношение для функций распределения меняется на противоположное: fG(E ') < fLV(E '). Отношение ${{{{f}_{{{\text{LV}}}}}(E_{{\max }}^{{}})} \mathord{\left/ {\vphantom {{{{f}_{{{\text{LV}}}}}(E_{{\max }}^{{}})} {{{f}_{{\text{G}}}}({{E}_{{\max }}}),}}} \right. \kern-0em} {{{f}_{{\text{G}}}}({{E}_{{\max }}}),}}$ как и параметр F (5), характеризует погрешность аппроксимации распределения Ландау–Вавилова fLV(E '), выполненного с помощью функции Гаусса fG(E '). Результаты расчетов по программам GEANT4 и FLUKA показали, что отношение ${{{{f}_{{{\text{LV}}}}}(E_{{\max }}^{{}})} \mathord{\left/ {\vphantom {{{{f}_{{{\text{LV}}}}}(E_{{\max }}^{{}})} {{{f}_{{\text{G}}}}(E)}}} \right. \kern-0em} {{{f}_{{\text{G}}}}(E)}}$ при изменении толщины мишени меняется мало и медленно возрастает с увеличением E0.

Рис. 3.

Распределение по энергии протонов с энергией E0 = 2 ГэВ после прохождения мишени из кремния толщиной x = 32 мкм: точки – экспериментальные данные [15]; сплошная линия – результаты расчетов по программе GEANT4 [13]; штриховая линия – результат аппроксимации экспериментальных данных функцией Гаусса с параметрами dE = 8.7 МэВ, Ω = 3.5 МэВ.

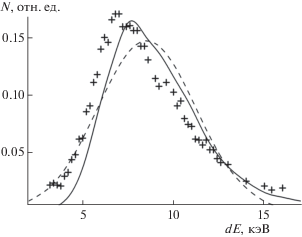
Трудно однозначно ответить на вопрос о том, какую модель лучше использовать для описания экспериментальных распределений быстрых ионов – распределение Ландау–Вавилова и результаты моделирования с использованием программ GEANT4 и FLUKA или распределение Гаусса и моделирование с помощью программы SRIM. С одной стороны, распределение Ландау–Вавилова качественно описывает медленное уменьшение количества ионов при больших потерях энергии, которое получается в эксперименте. С другой стороны, аппроксимация экспериментального распределения функцией Гаусса приводит к лучшему согласию с экспериментальными данными в области малых потерь энергии (рис. 3). Для описания распределения по энергии быстрых ионов лучше использовать обе модели, а отличия в теоретических оценках по ним интерпретировать как теоретическую погрешность выбора модели.

ЗАКЛЮЧЕНИЕ

Для описания распределения ионов по энергии после их прохождения через мишень имеются две модели, в которых это распределение описывается либо функцией Гаусса [12], либо функцией Ландау–Вавилова [13, 14]. Отличие этих подходов связано с учетом в распределении больших переданных импульсов.

При использовании распределения Гаусса предполагается, что столкновение иона с атомом мишени происходит при больших прицельных параметрах и ион в каждом столкновении теряет небольшой импульс. Для описания распределения ионов в этой модели используются либо теоретические оценки параметра ${{{{\Omega }^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{\Omega }^{{\text{2}}}}} {\Omega _{{\text{B}}}^{{\text{2}}}}}} \right. \kern-0em} {\Omega _{{\text{B}}}^{{\text{2}}}}}$ для тонкой мишени x ≤ xmax(E0), либо моделирование методом Монте-Карло с помощью программы SRIM для мишени произвольной толщины. Моделирование по программе SRIM позволило определить границы применимости приближения Бора. Параметр $\Omega _{{\text{B}}}^{{\text{2}}}$ можно использовать для описания распределения по энергии быстрых ионов с энергией E0 ≥ 0.5 МэВ/нуклон и мишеней толщиной x $ \ll $ $ \ll $ R(E0). Для статистического разброса потери энергии быстрых ионов в углероде (Zt = 6), кремнии (Zt = 14), меди (Zt = 29) и серебре (Zt = 47) получены эмпирические соотношения.

Экспериментальные распределения по энергии быстрых ионов характеризуются асимметрией, которая описывается распределением Ландау–Вавилова и учитывается при моделировании с использованием программ GEANT4 и FLUKA. Результаты расчетов показали, что в широком диапазоне значений E0 и толщины мишени асимметрия в распределении по энергии ионов сохраняется.

Список литературы

  1. Sigmund P. Particle Penetration and Radiation Effects. Volume 2: Penetration of Atomic and Molecular Ions. Cham–Heidelberg–New York–Dordrecht–London: Springer, 2014. 602 p.

  2. Бор H. Прохождение атомных частиц через вещество М.: ИЛ, 1950. 158 с.

  3. Lindhard J., Scharff M. // K. Dan. Vidensk. Selsk. Mat.-Fys. Medd. 1953. V. 27. № 15.

  4. Bonderup E., Hvelplund P. // Phys. Rev. A. 1971. V. 4. P. 562.

  5. Chu W.K. // Phys. Rev. A. 1976. V. l3. P. 2057.

  6. Brandt W., Kitagawa M. // Phys. Rev. B. 1982. V. 25. P. 5631.

  7. Ziegler J.F., Biersack J.P., Littmark U. The Stopping and Range of Ions in Solids. New York: Pergamon, 1985.

  8. Yang Q., O’Connor D.J., Wang Z. // Nucl. Instrum. Methods Phys. Res. B. 1991. V. 61. P. 149.

  9. Bishel H. // Nucl. Instrum. Methods Phys. Res. B. 1990. V. 52. P. 136.

  10. Landau L. // J. Phys. USSR. 1944. V. 8. P. 201.

  11. Вавилов П.В. // ЖЭТФ. 1957. Т. 32. С. 920.

  12. Ziegler J., Biersack J.P. SRIM: the Stopping and Range of Ions in Matter. www.srim.org.

  13. Allison J., Amako K., Apostolakis J. et al. // Nucl. Instrum. Methods Phys. Res. A. 2016. V. 835. P. 186. geant4.web.cern.ch.

  14. Böhlen T.T., Cerutti F., Chin M.P.W. et al. // Nuclear Data Sheets. 2014. V. 120. P. 211. www.fluka.org/fluka.php.

  15. Bak J.F., Burenkov A., Petersen J.B.B. et al. // Nucl. Phys. B. 1987. V. 288. P. 681.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал