1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 3, 2020

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 3, стр. 37-45

Оценка характеристик возбуждения рентгеновского излучения под воздействием электронного зонда при 2D- и 3D-моделировании методом Монте-Карло

В. В. Татаринов a, *, А. С. Кузаков b

a Институт геохимии им. А.П. Виноградова Сибирского отделения Российской академии наук
664033 Иркутск, Россия

b Иркутский филиал Института лазерной физики Сибирского отделения Российской академии наук
664033 Иркутск, Россия

* E-mail: tatarinov@igc.irk.ru

Поступила в редакцию 06.05.2019
После доработки 08.07.2019
Принята к публикации 14.07.2019

Полный текст (PDF)

Аннотация

Проведено сопоставление результатов двумерного и трехмерного моделирования процесса возбуждения рентгеновского излучения при электронно-зондовом микроанализе методом Монте-Карло. Сопоставление выполнено на примере описания распределения рентгеновского излучения в мишенях из чистых элементов Cu, Ag и Au, представляющих интерес при исследовании минералов золоторудных месторождений. Сопоставлены поправки на поглощение, рассчитанные с помощью моделей Монте-Карло для двумерной и трехмерной картины распределения рентгеновского излучения по глубине образца. Для электронов с энергией около 3 кэВ и более результаты расчета фактора поглощения при двумерном моделировании удовлетворительно согласуются с результатами расчетов при трехмерном моделировании. Построены функции радиального и латерального распределения рентгеновского излучения в образце, характеризующие пространственное разрешение электронно-зондового микроанализа. Получены аппроксимации, позволяющие оценить разрешение для элементов, которые, как правило, определяются по аналитическим линиям K-серии, и некоторых элементов, которые определяются по линиям L-серии.

Ключевые слова: рентгеноспектральный электронно-зондовый микроанализ, растровая электронная микроскопия, моделирование, Монте-Карло, возбуждение рентгеновского излучения, распределение по глубине образца, латеральное распределение, радиальное распределение, пространственное разрешение, локальность.

ВВЕДЕНИЕ

Для оценки зависимости интенсивности рентгеновского излучения, возбужденного сфокусированным пучком электронов, начиная с 1960-х годов получил распространение метод Монте-Карло, который позволяет моделировать траектории электронов в веществе и выполнять оценку влияния матрицы на результаты определения состава микровключений при рентгеноспектральном электронно-зондовом микроанализе (РСМА) [1, 2] и растровой электронной микроскопии (РЭМ) [3–5]. Обзор некоторых моделей Монте-Карло для РСМА и РЭМ приведен, например, в работах [6], [1], [7]. Среди ранних работ, на наш взгляд, следует отметить публикацию Лава, Кокса и Скотта [8] со ссылкой на отчет Кердженвена и Данкамба (1971) [9]. В основу модели [8] положено приближение непрерывного замедления электронов вдоль траектории, учитывающее неупругие взаимодействия электронов, при этом изменение направления траекторий электронов происходит в результате упругих столкновений. За последние два десятилетия появились более совершенные версии моделей Монте-Карло, которые положены в основу программного обеспечения для моделирования процессов взаимодействия электронов с веществом при РСМА и РЭМ (PENEPMA [10, 11], CASINO [12–14], DTSA-II [15, 16]). Современные модели включают в себя более детальное описание упругих и неупругих взаимодействий электронов, а геометрические условия возбуждения рентгеновского излучения и измерения аналитического сигнала в новых моделях представлены в более совершенной форме, чем в модели [8]. Тем не менее, простая полуэмпирическая модель [8] не потеряла свою актуальность и позволяет удовлетворительно описать функцию распределения рентгеновского излучения по глубине образца φ(ρz), которая определяет влияние матрицы на аналитический сигнал, причем в этом случае расчеты могут быть выполнены без использования специализированного программного обеспечения в широкодоступном решении MS Excel [17].

Модель [8] является квазиодномерной, то есть учитывает только одну пространственную координату z в глубину образца. В работе [17] эта модель была дополнена: были учтены две пространственные координаты. Несмотря на то, что двумерная модель является приближенной, она позволила качественно описать зависимость интенсивности аналитического сигнала от размера включений самородного золота в гомогенной сульфидной матрице. Позже сопоставимые результаты были получены и при трехмерном моделировании [18], в основу которого была также положена модель [8]. Геометрия возбуждения рентгеновского излучения при РСМА и РЭМ имеет аксиальную (цилиндрическую) симметрию. С этой точки зрения достаточно двух координат для описания картины взаимодействия электронов с веществом: радиальной координаты (т.е. расстояния от центра падающего пучка) и координаты глубины в образце.

В данной работе проведено сопоставление двумерной и трехмерной модели на примере описания распределения рентгеновского излучения в образце с начальной энергией электронов 20 кэВ при определении золота, серебра, меди и некоторых других элементов, энергии излучения которых лежат в области более 3 кэВ. Эти элементы представляют интерес при исследовании включений в сульфидных минералах золоторудных месторождений [19].

МОДЕЛИРОВАНИЕ ТРАЕКТОРИЙ ЭЛЕКТРОНОВ В ВЕЩЕСТВЕ МЕТОДОМ МОНТЕ-КАРЛО

Модель [8] основана на приближении непрерывного торможения, в котором потери энергии электронов описываются формулой Бете:

(1)
$\frac{{dE}}{{ds}} = - 7.{\text{85}}\rho \frac{Z}{A}\frac{1}{E}\ln \left( {\frac{{1166E}}{J}} \right),\,\,{{{\text{кэВ}}} \mathord{\left/ {\vphantom {{{\text{кэВ}}} {{\text{мкм}},}}} \right. \kern-0em} {{\text{мкм}},}}$
где E – энергия электрона (кэВ), s – длина пробега вдоль траектории в мкм; ρ – плотность вещества мишени (г/см3), Z и A – атомный номер и атомная масса элемента вещества, J – средний потенциал ионизации атома, который в приближении Вильсона равен J = 11.5Z (эВ) [20].

Траектория электрона разбивается на N равных интервалов Δs = smax/N, где smax – максимальный траекторный пробег, рассчитанный по формуле (1). В узлах траекторий на границах интервалов происходит изменение направления движения в результате упругого рассеяния. Энергия электрона в i-той точке траектории, соответствующей границе интервала, определяется с помощью процедуры численного решения уравнения (1). Такая простая модель в приближении непрерывного замедления позволяет удовлетворительно описать возбуждение рентгеновского излучения электронами с энергией больше 1 кэВ [21, 22].

Упругое рассеяние электронов описывается формулой Резерфорда [8], [23, 24]:

(2)
${\text{ctg(}}{\beta \mathord{\left/ {\vphantom {\beta {\text{2}}}} \right. \kern-0em} {\text{2}}}{\text{)}} = {{2p} \mathord{\left/ {\vphantom {{2p} b}} \right. \kern-0em} b},$
где β – угол рассеяния, p – прицельный параметр (минимальное расстояние между прямой, совпадающей с направлением движения электрона до акта рассеяния, и рассеивающим ядром). Значение b в Å рассчитывается из величин фундаментальных постоянных и численно равно b = 1.44 × × 10−2 × Z/E [8, 9], где энергия E выражена в кэВ.

Одним из преимуществ модели [8] является тот факт, что она является полуэмпирической: пространственное распределение излучения в образце определяется только параметром p0, который может быть откалиброван путем сравнения результатов расчетов фактора обратного рассеяния методом Монте-Карло с экспериментальными данными Данкамба и Рида [25–27]. Параметр p0 подбирается таким образом, чтобы обеспечить минимальное отклонение фактора обратного рассеяния, рассчитанного метом Монте-Карло по числу электронов, покинувших образец, с формулами Данкамба−Рида, которые используются в программном обеспечении микроанализаторов.

2D-Моделирование

Ранее в работе [17] мы использовали двумерный аналог трехмерной модели [8] для построения зависимости интенсивности рентгеновского излучения от размера микровключения в гомогенной матрице. В этом случае прицельный параметр p разыгрывается в интервале (−p0, +p0):

(3)
$p = - {{p}_{0}} + 2{{p}_{0}}\xi ,$
где ξ – случайное число, равномерно распределенное в интервале (0, 1), p0 – максимальный прицельный параметр.

Координаты точек, соответствующих границам интервалов, на которых происходит изменение направления движения электрона, определяются в соответствии с выражениями:

(4)
$\begin{gathered} {{z}_{0}} = 0,\,\,\,\,{{y}_{0}} = 0, \\ {{z}_{i}} = {{z}_{{i\, - \,1}}} + \Delta s\cos \sum\limits_{k\, = \,0}^{i\, - \,1} {{{\beta }_{k}}} , \\ {{y}_{i}} = {{y}_{{i\, - \,1}}} + \Delta s\sin \sum\limits_{k\, = \,\,0}^{i\, - \,1} {{{\beta }_{k}}} ,\,\,\,\,i \geqslant 1. \\ \end{gathered} $

В начале траектории угол между нормалью и направлением движения электрона βN = 0. Рассеяние начинается на границе поверхности образца при энергии падающих электронов E0, соответствующей ускоряющему напряжению электронного зонда. Угол βi для i ≥ 0 рассчитывается при использовании выражения (2). Для второго и последующих интервалов траектории угол между нормалью и направлением движения электрона представляет собой сумму углов βi для всех предыдущих узлов. Энергия электрона Ei в i-й точке траектории определяется численным решением уравнения:

(5)
${{E}_{i}} - {{E}_{{i\, - \,1}}} = 7.{\text{85}}\rho \frac{Z}{A}\frac{1}{{{{E}_{i}}}}\ln \left( {\frac{{1166}}{J}\frac{{{{E}_{i}}}}{2}} \right)(\Delta s),$
которое представляет собой конечноразностную аппроксимацию выражения (1). Так как целью моделирования является оценка области генерации рентгеновского излучения в образце, расчет траектории электрона прекращается, если он покидает образец (при zi < 0) или если энергия электрона становится меньше энергии Eq ионизации q-уровня выбранного элемента. Пример расчетных траекторий электронов для точечного зонда при E0 = 20 кэВ приведен на рис. 1.

Рис 1.

Расчетные траектории электронов при точечном зонде: (а) для меди; (б) для серебра; (в) для золота.

3D-Моделирование

На рис. 2 приведена общая схема части траектории электрона в образце при проведении 3D-моделирования.

Рис. 2.

Схема движения электрона при проведении РСМА и РЭМ.

Направляющие косинусы первого рассеяния на границе среды определяются из выражений [28]:

(6)
$u = \sin \beta \cos \phi ,\,\,\,\,\upsilon = \sin \beta \sin \phi ,\,\,\,\,\omega = \cos \beta ,$
где угол β вычисляется по формуле Резерфорда, а угол φ равномерно распределен в интервале (0, 2π), ϕ = 2πξ, ξ ∈ (0, 1) – случайное число.

Направляющие косинусы для второго и последующих интервалов траектории определяются из выражений:

(7)
$\begin{gathered} u{\kern 1pt} ' = u\cos \beta + \frac{{\sin \beta }}{{{{{(1 - {{\omega }^{2}})}}^{{0.5}}}}}\left[ {u\omega \cos \varphi - \upsilon \sin \varphi } \right], \\ \upsilon {\kern 1pt} ' = \upsilon \cos \beta + \frac{{\sin \beta }}{{{{{(1 - {{\omega }^{2}})}}^{{0.5}}}}}\left[ {\upsilon \omega \cos \varphi + u\sin \varphi } \right], \\ \omega {\kern 1pt} ' = \omega \cos \beta - {{(1 - {{\omega }^{2}})}^{{0.5}}}\sin \beta \cos \varphi . \\ \end{gathered} $

На рис. 2 dn = (u, υ, ω) и dn+ 1 = (u', υ', ω') приведены направляющие косинусов до и после рассеяния соответственно. Координата точки r = = (xn, yn, zn), соответствующей границе между интервалами рассеяния, определяется из выражения:

(8)
${{r}_{{n\, + \,1}}} = {{r}_{n}} + \Delta s{{d}_{n}}.$

Прицельный параметр разыгрывается в соответствии с выражением:

(9)
$p = {{p}_{0}}\xi .$
Угол рассеяния определяется из выражения (2) и азимутальный угол предполагается равновероятным в интервале (0, 2π).

Описанный алгоритм вычислений был реализован на языке C# в авторской Программе для моделирования процессов взаимодействия электронов с веществом “Герон” [29] для операционной системы Windows. Программа предполагает использование операторов вращения для ортов друг относительно друга последовательно без преобразования основного базиса. Данный принцип позволяет существенно упростить расчет траекторий электронов в образце и является полным аналогом последовательных расчетов рассеяния и азимутального вращения вектора перемещения электрона в рамках модели Монте-Карло. Траектории электронов были поделены на 200 интервалов, расчеты проводились по 5 тыс. траекторий. Точность решения уравнения Бете и поиска p0 задавалась равной 0.001, что обеспечило погрешность счета для оценки фактора обратного рассеяния на уровне 0.03% и менее.

СРАВНЕНИЕ РЕЗУЛЬТАТОВ 2D- И 3D-МОДЕЛИРОВАНИЯ

Были построены функции распределения рентгеновского излучения по глубине образца φ(ρz) с помощью 2D- и 3D-моделей. Функция φ(ρz) представляет собой зависимость числа ионизаций q-уровня элемента от глубины в образце. В выбранном i-м слое Δzi число ионизаций (ΔN)i будет равно:

(10)
${{(\Delta N)}_{i}} = {{n}_{i}}Q({{U}_{i}})\Delta s,$
где ni = ρNA/A – число атомов в единице объема вещества; NA – число Авогадро, A – атомная масса, Δs – пробег электрона в слое толщиной Δz.

В каждом интервале по глубине в образце рассчитывается поглощение рентгеновского излучения: exp(−χρz), где χ = (μ/ρ)cosec θ, (μ/ρ) – массовый коэффициент поглощения излучения аналитической линии выбранного элемента, θ – угол отбора излучения (θ = 40° для большинства микроанализаторов), z – глубина. Фактор поглощения может быть выражен через функцию φ(ρz) [1]:

(11)
$f\left( \chi \right) = \frac{{\int\limits_0^{\rho {{s}_{{\max }}}} {\varphi \left( {\rho z} \right)\exp \left( { - \chi \rho z} \right)d\left( {\rho z} \right)} }}{{\int\limits_0^{\rho {{s}_{{\max }}}} {\varphi \left( {\rho z} \right)d\left( {\rho z} \right)} }}.$

Фактор ƒ(χ), рассчитанный методом Монте-Карло, сравнивался со значением, полученным по формуле Филибера с параметрами Гейнриха [20]:

(12)
$\begin{gathered} f{{\left( \chi \right)}_{{{\text{Phil}}}}} = \frac{{1 + h}}{{\left( {1 + {\chi \mathord{\left/ {\vphantom {\chi \sigma }} \right. \kern-0em} \sigma }} \right)\left( {1 + h\left( {1 + {\chi \mathord{\left/ {\vphantom {\chi \sigma }} \right. \kern-0em} \sigma }} \right)} \right)}}, \\ h = 1.2A{\text{/}}{{Z}^{2}},\,\,\,\,\sigma = \frac{{4.5 \times {{{10}}^{5}}}}{{E_{0}^{{1.65}} - E_{q}^{{1.65}}}}. \\ \end{gathered} $

На рис. 3 приведены функции φ(ρz), построенные по 2D- и 3D-моделям для Cu, Ag и Au при E0 = = 20 кэВ, а в табл. 1 соответствующие им поправки на поглощение.

Рис. 3.

Сопоставление функций φ(ρz), построенных с помощью 3D- и 2D-моделей Монте-Карло: (а) для CuKα, AgLα; (б) для AuLα, AgMα.

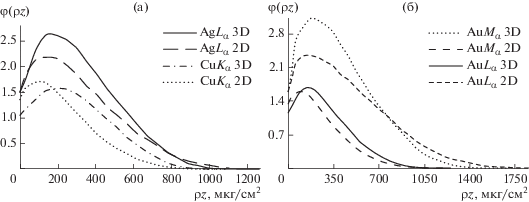
Таблица 1.  

Сопоставление поправок на поглощение для 2D- и 3D-моделей

Линия Энергия, кэВ ƒ(χ)Phil Расчет ƒ(χ) методом Монте-Карло Δƒ(χ)
2D–3D
2D 3D
CuKα 8.048 0.987 0.987 0.985 0.002
AgLα 2.984 0.859 0.823 0.845 0.022
AuLα 9.713 0.977 0.963 0.966 0.003
AuMα 2.125 0.758 0.627 0.731 0.104

Из табл. 1 и рис. 3б видно, что для относительно низкой энергии AuMα-линии расчеты по 2D-модели приводят с существенному занижению фактора поглощения. Несмотря на то, что на рис. 3 все кривые φ(ρz) для 2D-модели систематически занижены и имеют смещение пиков по сравнению с кривыми для 3D-модели, интегрирование функций φ(ρz) для 2D- и 3D-моделей согласно данным в табл. 1 приводит к близким значениям ƒ(χ). Таким образом, для энергий около 3 кэВ и более не наблюдается существенного отличия при моделировании распределения рентгеновского излучения по глубине образца в 2D и в 3D.

Расчеты, проведенные с помощью описанной 3D-модели, были сопоставлены с литературными данными Вернера [7], Паквуда и Брауна [30, 31]. Из рис. 4 видно, что функции φ(ρz), построенные методом Монте-Карло, имеют незначительное смещение по сравнению с эмпирическими данными, но площадь под графиком и характер поведения φ(ρz) находятся в согласии с ранее опубликованными данными.

Рис. 4.

Сопоставление функций φ(ρz), построенных методом Монте-Карло, с литературными данными: (а) в приближении непрерывного замедления (CSDA) для Si Kα при E0 = 10 кэВ [7]; (б) для Cu Kα при E0 = 20 кэВ [30, 31].

ОЦЕНКА ЛАТЕРАЛЬНОГО И РАДИАЛЬНОГО РАСПРЕДЕЛЕНИЯ

При проведении анализа тонкодисперсных включений микронных и субмикронных размеров часть электронов зонда может попадать не только на анализируемую частицу, но и на окружающую ее матрицу, что существенно искажает результаты определения состава включений. В этом случае для описания распределения рентгеновского излучения в образце построения функции φ(ρz) недостаточно, поскольку размер таких включений часто сопоставим с областью генерации рентгеновского излучения в образце. Для оценки локальности анализа мы строили функции латерального и радиального распределения рентгеновского излучения в образце, которые характеризуют разрешение количественного анализа. Латеральное распределение по оси x в двумерном случае должно отличаться от радиального распределения в трехмерном случае, поскольку для трехмерного случая распределение на плоскости x–z является лишь проекцией радиального распределения на эту плоскость.

На рис. 5 приведены зависимости относительной интенсивности рентгеновского излучения I от расстояния l до точки измерения относительно центра падающего пучка электронного зонда для AuLα-линии, полученные при моделировании методом Монте-Карло.

Рис. 5.

Сопоставление латерального распределения в 2D и радиального распределения в 3D для AuLα при E0 = 20 кэВ для точечного зонда.

Из рис. 5 видно, что латеральное и радиальное распределение сходятся к нулевому значению интенсивности при близких значениях l, следовательно, оба распределения должны приводить к сопоставимым оценкам разрешения электронного зонда.

В книге Рида [20] приведена формула для оценки разрешения электронного зонда для меди:

(13)
$d = {{0.077\left( {E_{0}^{{1.5}} - E_{q}^{{1.5}}} \right)} \mathord{\left/ {\vphantom {{0.077\left( {E_{0}^{{1.5}} - E_{q}^{{1.5}}} \right)} \rho }} \right. \kern-0em} \rho },\,\,{\text{мкм}}{\text{.}}$
Экспериментально установлено, что пространственное разрешение количественного анализа может быть определено путем оценки размера области, содержащей 99% генерируемого излучения, и эта область должна быть примерно в три раза больше, чем оценка по выражению (13) [20]. На рис. 6 приведены латеральные распределения для AuLα-, AgLα-, и CuKα-линий. Выделенные точки на графиках соответствуют границе области латерального распределения l99, на которую приходится 99% интенсивности рентгеновского излучения.

Рис. 6.

Сопоставление латеральных распределений для AuLα, AgLα, и CuKα при E0 = 20 кэВ для точечного зонда.

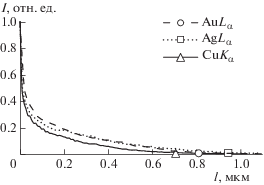
Поскольку латеральные распределения на рис. 6, были построены от центра падающего пучка электронов, а в отрицательной области значений l график имеет симметричный вид, разрешение количественного анализа может быть определено как удвоенное расстояние l99. Используя данные латеральных распределений для элементов с Z от 11 до 34, полученных при моделировании методом Монте-Карло при E0 = 20 кэВ для точечного зонда, мы получили аппроксимацию, позволяющую оценить разрешение количественного РСМА в зависимости от атомного номера Z для элементов, которые, как правило, определяются при проведении РСМА по аналитическим линиям K-серии:

(14)
${{\left( {2{{l}_{{99}}}} \right)}_{K}} = 0.00394{{Z}^{{0.5}}}\left( {E_{0}^{{1.5}} - E_{q}^{{1.5}}} \right),\,\,{\text{мкм}}{\text{.}}$

На рис. 7 приведен график зависимости 2l99 от Z для элементов, которые определяются по линиям K-серии при E0 = 20 кэВ. Кривая соответствует аппроксимации по формуле (14) с коэффициентом корреляции 0.998, а точки на графике соответствуют расчетам методом Монте-Карло.

Рис. 7.

Зависимость пространственного разрешения РСМА от атомного номера элемента для аналитических линий K-серии.

Для аналитических линий L-серии расчеты латеральных распределений методом Монте-Карло проводились в диапазонах Z от 44 до 50 и от 74 до 82, в которых расположены элементы, представляющие интерес при исследовании минералов золоторудных месторождений. Была получена аппроксимация с коэффициентом корреляции 0.998, которая позволяет определить пространственное разрешение РСМА для данных элементов:

(15)
${{\left( {2{{l}_{{99}}}} \right)}_{L}} = 0.00159{{Z}^{{0.7}}}\left( {E_{0}^{{1.5}} - E_{q}^{{1.5}}} \right),\,\,{\text{мкм}}{\text{.}}$

В табл. 2 приведены значения пространственного разрешения, рассчитанные методом Монте-Карло по границе l99 и по формулам (14) и (15), для некоторых элементов, представляющих интерес при исследовании тонкодисперсных включений самородного золота, серебра и элементов платиновой группы в минералах золоторудных месторождений. Из табл. 2 видно, что отклонение расчетов методом Монте-Карло от аппроксимаций (14) и (15) не превышает 0.2 мкм.

Таблица 2.  

Расчет пространственного разрешения РСМА при E0 = 20 кэВ для точечного зонда

Z ρ, г/см3 Линия Eq, кэВ smax, мкм 2l99, мкм (2l99)K,L, мкм Δ(2l99), мкм
29 8.92 CuKα 8.979 1.76 1.34 1.33 0.01
34 4.79 SeKα 12.658 3.64 1.08 1.02 0.06
44 12.41 RuLα 2.838 1.50 1.96 1.91 0.05
45 12.41 RhLα 3.004 1.51 1.94 1.93 0.01
46 12.02 PdLα 3.173 1.58 1.92 1.95 0.03
47 10.50 AgLα 3.351 1.81 1.89 1.95 0.06
76 22.59 OsLα 10.871 1.09 1.81 1.77 0.04
77 22.65 IrLα 11.215 1.09 1.72 1.73 0.01
78 21.45 PtLα 11.564 1.16 1.80 1.69 0.11
79 19.32 AuLα 11.919 1.29 1.74 1.64 0.10
80 13.55 HgLα 12.284 1.86 1.41 1.55 0.14
82 11.34 PbLα 13.035 2.26 1.52 1.48 0.04

Пространственное разрешение для объемного зонда по сравнению с точечным зондом увеличивается на величину диаметра зонда, что подтверждается результатами построения латеральных распределений для зондов с различным диаметром падающего пучка на рис. 8. Для каждого типа зонда усреднение интенсивности проводилось по 9 тыс. траекториям электронов с одинаковым пространственным интервалом между точками расчета интенсивности.

Рис. 8.

Латеральные распределения рентгеновского излучения для объемных электронных зондов различных диаметров.

Таким образом, для оценки локальности количественного РСМА к величине 2l99 необходимо прибавить диаметр зонда. Полученное значение позволяет оценить минимальный размер тонкодисперсных включений, при котором они могут быть проанализированы без захвата элементов матрицы при условии, что электроны зонда будут сфокусированы в пятно, расположенное по центру анализируемого включения.

ЗАКЛЮЧЕНИЕ

Результаты моделирования процессов возбуждения рентгеновского излучения в образце при проведении РСМА с использованием специализированного программного обеспечения свидетельствуют о том, что для расчета поправок на поглощение для линий элементов с энергией около 3 кэВ и более можно использовать двумерную модель Монте-Карло. Двумерная модель значительно проще в реализации и может быть запрограммирована в широкодоступном MS Excel. Несмотря на то, что при построении функции распределения рентгеновского излучения по глубине образца наблюдается смещение максимумов φ(ρz) при проведении расчетов по 2D-модели, результаты интегрирования функции φ(ρz) существенно не отличаются при 2D- и 3D-расчетах.

Функции латерального и радиального распределения рентгеновского излучения, построенные в ходе моделирования методом Монте-Карло, позволяют оценить пространственное разрешение количественного анализа. Построены аппроксимации, позволяющие оценить разрешение РСМА в зависимости от атомного номера для элементов, определяемых по аналитическим линиями K-серии, и некоторых элементов, определяемых по линиям L-серии, которые представляют интерес при изучении тонкодисперсных включений самородного золота, серебра и элементов платиновой группы в минералах золоторудных месторождений.

Список литературы

  1. Афонин В.П., Лебедь В.И. Метод Монте-Карло в рентгеноспектральном микроанализе. Новосибирск: Наука. Сиб. отд-ние, 1989. 110 с.

  2. Павлова Л.А., Белозерова О.Ю., Парадина Л.Ф., Суворова Л.Ф. Рентгеноспектральный электронно-зондовый микроанализ природных объектов. Новосибирск: Наука, 2000. 224 с.

  3. Новиков Ю.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 8. С. 73. https://doi.org/10.7868/S020735281708011X

  4. Новиков Ю.А. // Поверхность. Рентген., синхротр, и нейтрон. исслед. 2018. № 2. С. 96. https://doi.org/10.7868/S0207352818020166

  5. Новиков Ю.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2018. № 5. С. 56. https://doi.org/10.7868/S0207352818050062

  6. Use of Monte Carlo Calculations in Electron Probe Microanalysis, NBS Special Publication 460. Washington, D.C.: U.S. Department of Commerce, National Bureau of Standards, 1976. 164 pp.

  7. Werner W.S.M. // Surf. Interface Anal. 2001. V. 31. № 3. P. 141. https://doi.org/10.1002/sia.973

  8. Love G., Cox M.G.C., Scott V.D. // J. Phys. D: Appl. Phys. 1977. V. 10. № 1. P. 7. https://doi.org/10.1088/0022-3727/10/1/002

  9. Curgenven L., Duncumb P. Simulation of Electron Trajectories in a Solid Target by a Simple Monte Carlo Technique. T. I. Report № 303. Hinxton: Tube Investments Research Laboratories, 1971.

  10. Llovet X., Salvat F. // Microsc. Microanal. 2017. V. 23. № 3. P. 634. https://doi.org/10.1017/S1431927617000526

  11. Salvat F., Llovet X., Fernández-Varea J.M., Sempau J. // Microchim. Acta. 2006. V. 155. № 1–2. P. 67. https://doi.org/10.1007/s00604-006-0508-y

  12. Hovington P., Drouin D., Gauvin R. // Scanning. 1997. V. 19. № 1. P. 1. https://doi.org/10.1002/sca.4950190101

  13. Drouin D., Couture R.A., Joly D. et al. // Scanning. 2007. V. 29. № 3. P. 92. https://doi.org/10.1002/sca.20000

  14. Demers H., Poirier-Demers N., Couture A.R. et al. // Scanning. 2011. V. 33. № 3. P. 135. https://doi.org/10.1002/sca.20262

  15. Ritchie N.W.M. // Surf. Interface Anal. 2005. V. 37. № 11. P. 1006. https://doi.org/10.1002/sia.2093

  16. Ritchie N.W.M. NIST DTSA-II [Электронный ресурс] // Material Measurement Laboratory, National Institute of Standards and Technology. https://www.cstl.nist.gov/div837/837.02/epq/dtsa2/index. html

  17. Татаринов В.В., Финкельштейн А.Л., Кравцова Р.Г., Павлова Л.А. // Аналитика и контроль. 2017. Т. 21. № 3. С. 208. https://doi.org/10.15826/analitika.2017.21.3.006

  18. Finkelshtein A.L., Tatarinov V.V., Finkelstein E. et al. // X-Ray Spectrom. 2018. 47. № 6. P. 423. https://doi.org/10.1002/xrs.2967

  19. Кравцова Р.Г., Таусон В.Л., Никитенко Е.М. // Геохимия. 2015. № 11. С. 991. https://doi.org/10.7868/S0016752515090034

  20. Рид С.Дж.Б. Электронно-зондовый микроанализ: Пер. с англ. Москва: Мир, 1979. 423 с.

  21. Statham P.J. // X-Ray Spectrom. 1976. V. 5. № 3. P. 154. https://doi.org/10.1002/xrs.1300050310

  22. Ding Z.J., Shimizu R., Obori K. // J. Appl. Phys. 1994. V. 76. № 11. P. 7180. https://doi.org/10.1063/1.357998

  23. Малви Т., Скотт В.Д., Рид С.Дж.Б. и др. Количественный электронно-зондовый микроанализ / Пер. с англ. М.: Мир, 1986. 352 с.

  24. Физические основы рентгеноспектрального локального анализа / Пер. с англ. под ред. Боровского И.Б. М.: Главная редакция физико-математической литературы изд-ва “Наука”, 1973. 311 с.

  25. Duncumb P., Reed S.J.B. / NBS Special Publication 298. Washington, D.C.: U.S. Department of Commerce, National Bureau of Standards, 1968. P. 133.

  26. Joy D.C. Monte Carlo Modeling for Electron Microscopy and Microanalysis. New York: Oxford University Press, 1995. 216 p. https://doi.org/10.1002/1097-0029(19961201)35:5% 3C413::AID-JEMT1070350502%3E3.0.CO;2-6

  27. Goldstein J.I., Newbury D.E., Michael J.R. et al. Scanning Electron Microscopy and X-Ray Microanalysis. New York: Springer, 2017. 550 p.  https://doi.org/10.1007/978-1-4939-6676-9

  28. Salvat F. PENELOPE-2014: A Code System for Monte Carlo Simulation of Electron and Photon Transport. OECD Nuclear Energy Agency, 2015. 406 p. URL: https://www.oecd-nea.org/science/docs/2015/nsc-doc2015-3.pdf

  29. Свидетельство о гос. регистрации прЭВМ № 2 019 614 428. Программа для моделирования процессов взаимодействия электронов с веществом “Герон” / Татаринов В.В., Кузаков А.С., Финкельштейн А.Л.; заявитель и правообладатель ИГХ СО РАН (RU). № 2 019 612 941; заявл. 22.03.2019; опубл. 04.04.2019 / Бюл. № 4. 1 с.

  30. Packwood R.H., Brown J.D. // X-Ray Spectrom. 1981. V. 10. № 3. P. 138. https://doi.org/10.1002/xrs.1300100311

  31. Brown J.D., Packwood R.H. Quantitative Electron Probe Microanalysis Using Gaussian ϕ(ρz) Curves // X-Ray Spectrom. 1982. V. 11. № 4. P. 187. https://doi.org/10.1002/xrs.1300110411

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал