Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 6, стр. 43-53
Когерентное рентгеновское излучение, генерируемое вблизи оси пучка релятивистских электронов в искусственной периодической структуре
С. В. Блажевич a, *, Ю. А. Дрыгина a, О. Ю. Шевчук a, А. В. Носков b, **
a Белгородский государственный университет
308015 Белгород, Россия
b Белгородский государственный технологический университет имени В.Г. Шухова
308012 Белгород, Россия
* E-mail: blazh@bsu.edu.ru
** E-mail: noskovbupk@mail.ru
Поступила в редакцию 07.10.2019
После доработки 10.12.2019
Принята к публикации 11.12.2019
Аннотация
Развита теория когерентного рентгеновского излучения, возбуждаемого пучком релятивистских электронов в искусственной периодической структуре и распространяющегося вдоль оси электронного пучка. В геометрии рассеяния Брэгга получены выражения, описывающие спектрально-угловую плотность параметрического рентгеновского излучения в направлении, близком к вектору скорости электронов (ПРИВ), переходного излучения (ПИ), и их интерференцию. Анализ, проведенный на основе полученных выражений для спектрально-угловой плотности, показывает возможности их использования для определения оптимальных параметров эксперимента по регистрации ПРИВ. Показаны преимущества эксперимента по регистрации ПРИВ при низкой энергии электронов (${{E}_{e}} \leqslant $ 50 МэВ).
1. ВВЕДЕНИЕ
Когерентное рентгеновское излучение релятивистского электрона в искусственной периодической структуре в приближении динамической теории дифракции в виде вкладов параметрического рентгеновского излучения (ПРИ) и дифрагированного переходного излучения (ДПИ) впервые рассматривалось в работе [1]. ПРИ в искусственной периодической структуре возникает вследствие дифракции псевдо-фотонов кулоновского поля релятивистского электрона на слоях мишени аналогично тому, как вследствие дифракции на системе параллельных атомных плоскостей возникает ПРИ в монокристалле [2, 3]. Дифрагированное переходное излучение является следствием дифракции на слоях мишени фотонов переходного излучения, генерируемого на входной поверхности мишени, по аналогии с ДПИ в монокристалле [4–6]. Динамическая теория излучения релятивистских электронов в периодических слоистых средах [1] хорошо описывает экспериментальные данные, представленные в работе [7].
Необходимо отметить, что традиционно процесс излучения в периодических слоистых средах рассматривался в геометрии рассеяния Брэгга и только для частного случая симметричного отражения поля электрона относительно поверхности мишени, когда угол между поверхностью мишени и отражающими плоскостями равен нулю. Такое рассмотрение было проведено и в работе [1]. Процесс когерентного рентгеновского излучения релятивистского электрона в периодической слоистой структуре в общем случае асимметричного отражения в геометрии рассеяния Брэгга впервые рассматривался в работе [8], а позже для пучков релятивистских электронов − в работе [9]. Проявление эффектов динамической дифракции в когерентном рентгеновском излучении релятивистских электронов, пересекающих искусственную периодическую структуру, в геометрии рассеяния Лауэ подробно проанализировано в работе [10].
Теория ПРИ релятивистской частицы в монокристалле предсказывает излучение не только вблизи направления рассеяния Брэгга, но также и вблизи направления скорости частицы (ПРИВ − ПРИ вперед) [11, 12]. Теоретическое описание ПРИВ релятивистских электронов в монокристалле в общем случае асимметричного относительно поверхности мишени отражения кулоновского поля электрона в геометрии рассеяния Лауэ было представлено в работе [13]. Детальное теоретическое описание ПРИВ релятивистского электрона в монокристалле для случая симметричного отражения в геометрии рассеяния Брэгга было дано в работе [14]. ПРИВ обнаружено экспериментально только в монокристалле и только в геометрии рассеяния Лауэ [15].
Необходимо отметить, что ПРИВ релятивистских электронов в периодической слоистой среде экспериментально не наблюдалось. ПРИВ является динамическим эффектом, и эго экспериментальная регистрация очень важна для динамической теории когерентного рентгеновского излучения.
В настоящей работе рассматривается когерентное рентгеновское излучение пучка релятивистских электронов в периодической слоистой среде в направлении, близком к направлению оси пучка в геометрии рассеяния Брэгга, для общего случая асимметричного отражения поля электрона относительно поверхности мишени. Получены и исследованы выражения, описывающие спектрально-угловую плотность излучения.
ГЕОМЕТРИЯ ПРОЦЕССА ИЗЛУЧЕНИЯ
Рассмотрим пучок релятивистских электронов, пересекающих периодическую структуру в геометрии рассеяния Брэгга (рис. 1), состоящую из чередующихся слоев толщиной ${{l}_{1}}$ и ${{l}_{2}},$ и диэлектрическими восприимчивостями, соответственно, ${{\chi }_{1}}$ и ${{\chi }_{2}}$ ($T = {{l}_{1}} + {{l}_{2}}$ период слоистой мишени). Отражающие слои расположены под некоторым углом $\delta $ к поверхности мишени (рис. 1), что соответствует случаю асимметричного отражения поля излучения ($\delta = 0$ − частный случай симметричного отражения). Введем угловые переменные $\psi {\text{,}}$ ${\mathbf{\theta }}{\kern 1pt} '$ и ${\mathbf{\theta }}$ в соответствии с определениями скорости релятивистского электрона ${\mathbf{V}}$ и единичных векторов: ${\mathbf{n}}$ (в направлении импульса фотона, излученного вблизи направления вектора скорости электрона) и ${{{\mathbf{n}}}_{{\mathbf{g}}}}$ (в направлении рассеяния Брэгга):
(1)
$\begin{gathered} {\mathbf{V}} = \left( {1 - \frac{1}{2}{{\gamma }^{{ - 2}}} - \frac{1}{2}{{\psi }^{2}}} \right){{{\mathbf{e}}}_{1}} + \psi ,\,\,\,\,{{{\mathbf{e}}}_{1}}\psi = 0, \\ {\mathbf{n}} = \left( {1 - \frac{1}{2}\theta _{{}}^{2}} \right){{{\mathbf{e}}}_{1}} + {\mathbf{\theta }},\,\,\,\,{{{\mathbf{e}}}_{1}}{\mathbf{\theta }} = 0,\,\,\,\,{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}} = \cos 2{{\theta }_{{\text{B}}}}, \\ {{{\mathbf{n}}}_{{\mathbf{g}}}} = \left( {1 - \frac{1}{2}\theta {\kern 1pt} {{'}^{2}}} \right){{{\mathbf{e}}}_{2}} + {\mathbf{\theta }}{\kern 1pt} ',\,\,\,\,{{{\mathbf{e}}}_{2}}{\mathbf{\theta }} = 0, \\ \end{gathered} $СПЕКТРАЛЬНО-УГЛОВАЯ ПЛОТНОСТЬ ИЗЛУЧЕНИЯ
При решении задачи будем рассматривать уравнение для Фурье-образа ${\mathbf{E}}({\mathbf{k}},\omega )$ = $\int {dt{{d}^{3}}r} {\text{ }}{\mathbf{E}}({\mathbf{r}},t) \times $ $ \times \,\,\exp \left( {i\omega t - i{\mathbf{kr}}} \right)$ электромагнитного поля, возбуждаемого электроном в периодической слоистой среде, следующее из системы уравнений Максвелла:
(2)
$\begin{gathered} ({{k}^{2}} - {{\omega }^{2}}(1 + {{\chi }_{0}})){\mathbf{E}}({\mathbf{k}},\omega ) - {\mathbf{k}}({\mathbf{kE}}({\mathbf{k}},\omega )) - \\ - \,\,{{\omega }^{2}}\sum\limits_{\mathbf{g}} {\chi {{{_{{ - {\mathbf{g}}}}^{'}}}_{{}}}{\mathbf{E}}({\mathbf{k}} + {\mathbf{g}},\omega )} = 4\pi i\omega {\mathbf{J}}({\mathbf{k}},\omega ), \\ \end{gathered} $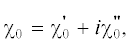

Вектор ${\mathbf{g}}$ аналогичен вектору обратной решетке в кристалле, он перпендикулярен слоям мишени и его длина ровна $g = \frac{{2\pi }}{Т}n,$ $n = 0, \pm 1, \pm 2,...$ В случае ${{\chi }_{{ - {\mathbf{g}}}}} = 0$ выражение (2) описывает электрическое поле в однородной аморфной среде.
Величины ${{\chi }_{0}}$ и ${{\chi }_{{\mathbf{g}}}}$ в рассматриваемой периодической структуре имеют следующий вид:
(4)
$\begin{gathered} {{\chi }_{0}}(\omega ) = \frac{{{{l}_{1}}}}{T}{{\chi }_{1}} + \frac{{{{l}_{2}}}}{T}{{\chi }_{2}}, \\ {{\chi }_{{\mathbf{g}}}}(\omega ) = \frac{{\exp \left( { - ig{{l}_{1}}} \right) - 1}}{{igТ}}\left( {{{\chi }_{2}} - {{\chi }_{1}}} \right). \\ \end{gathered} $Влияние вещества на формирование и распространения излучения определяется только величинами ${{\chi }_{0}}(\omega )\,$ и ${{\chi }_{{\mathbf{g}}}}(\omega ).$ При этом вблизи передней и задней границы мишени (на толщине порядка толщины наибольшего слоя) эти величины будут меняться вдоль границы, так как будут меняться вдоль границы толщины слоев ${{l}_{1}}$ и ${{l}_{2}},$ так как они будут обрезаны. Но, поскольку когерентное формирование и рассеяния излучения происходит на большом количестве слоев, изменение рассматриваемых величин ${{\chi }_{0}}(\omega )$ и ${{\chi }_{{\mathbf{g}}}}(\omega )$ вблизи границ мишени никак не скажется на спектрально-угловой плотности излучения.
Так как излучаемое релятивистским электроном электромагнитное поле в рентгеновском диапазоне частот является поперечным, то падающая ${\mathbf{E}}({\mathbf{k}},\omega )$ и дифрагированная в периодической слоистой среде ${\mathbf{E}}({\mathbf{k}} + {\mathbf{g}},\omega )$ электромагнитные волны, определяются двумя амплитудами с разными значениями поперечной поляризации:
(6)
$\begin{gathered} {\mathbf{E}}({\mathbf{k}},\omega ) = E_{0}^{{(1)}}({\mathbf{k}},\omega ){\mathbf{e}}_{0}^{{(1)}} + E_{0}^{{(2)}}({\mathbf{k}},\omega ){\mathbf{e}}_{0}^{{(2)}}, \\ {\mathbf{E}}({\mathbf{k}} + {\mathbf{g}},\omega ) = E_{{\mathbf{g}}}^{{(1)}}({\mathbf{k}},\omega ){\mathbf{e}}_{1}^{{(1)}} + E_{{\mathbf{g}}}^{{(2)}}({\mathbf{k}},\omega ){\mathbf{e}}_{1}^{{(2)}}, \\ \end{gathered} $(7)
$\left\{ \begin{gathered} ({{\omega }^{2}}(1 + {{\chi }_{0}}) - {{k}^{2}})E_{0}^{{(s)}} + {{\omega }^{2}}{{\chi }_{{ - {\mathbf{g}}}}}{{C}^{{(s,\tau )}}}E_{{\mathbf{g}}}^{{(s)}} = 8{{\pi }^{2}}ie\omega {\mathbf{e}}_{{\mathbf{0}}}^{{{\text{(}}s{\text{)}}}}{\mathbf{V}}\delta (\omega - {\mathbf{kV}}), \hfill \\ {{\omega }^{2}}{{\chi }_{{\mathbf{g}}}}{{C}^{{(s,\tau )}}}E_{0}^{{(s)}} + ({{\omega }^{2}}(1 + {{\chi }_{0}}) - k_{{\mathbf{g}}}^{2})E_{{\mathbf{g}}}^{{(s)}} = 0. \hfill \\ \end{gathered} \right.$(8)
$\begin{gathered} {{C}^{{(s,\tau )}}} = {\mathbf{e}}_{0}^{{(s)}}{\mathbf{e}}_{1}^{{(s)}} = {{( - 1)}^{\tau }}{{C}^{{(s)}}},\,\,\,\,{{С}^{{(1)}}} = 1, \\ {{С}^{{(2)}}} = \left| {\cos 2{{\theta }_{{\text{B}}}}} \right|,\,\,\,\,{\mathbf{e}}_{{\mathbf{0}}}^{{{\mathbf{(}}1{\mathbf{)}}}}{\mathbf{V}} = {{\theta }_{ \bot }} - {{\psi }_{ \bot }}, \\ \,{\mathbf{e}}_{{\mathbf{0}}}^{{{\mathbf{(}}2{\mathbf{)}}}}{\mathbf{V}} = {{\theta }_{\parallel }} + {{\psi }_{\parallel }}, \\ \end{gathered} $Рассмотрим наиболее интересный случай, когда длина пути электрона в пластинке ${{L}_{e}} = L{\text{/}}\sin ({{\theta }_{{\text{B}}}} + $ $ + \,\,\delta )$ больше длины экстинкции рентгеновских волн в периодической слоистой среде, то есть
${{b}^{{(s)}}} = {{L}_{e}}{\text{/}}2L_{{{\text{ext}}}}^{{(s)}},$ что является условием проявления динамических эффектов в излучении. В то же время
будем рассматривать периодическую слоистую среду как тонкую непоглощающую мишень,
в которой длина пути фотона в мишени $({{L}_{f}} \approx {{L}_{e}})$ будет значительно меньше длины поглощения рентгеновских волн в периодической слоистой
среде ${{L}_{{abs}}}$ =  $(r = {{l}_{2}}{\text{/}}{{l}_{1}}),$ то есть ${{L}_{f}}{\text{/}}{{L}_{{abs}}} \ll 1.$ Для процесса когерентного рентгеновского излучения пучка релятивистских электронов
аналогично работе [8], получим выражение, описывающее спектрально-угловую плотность ПРИВ:
$(r = {{l}_{2}}{\text{/}}{{l}_{1}}),$ то есть ${{L}_{f}}{\text{/}}{{L}_{{abs}}} \ll 1.$ Для процесса когерентного рентгеновского излучения пучка релятивистских электронов
аналогично работе [8], получим выражение, описывающее спектрально-угловую плотность ПРИВ:
(9а)
$\begin{gathered} \omega \frac{{{{d}^{2}}N_{{{\text{ПРИВ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \\ = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{{{{\Omega }^{{(s)}}}^{2}}}{{{{{\left( {{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} - {{\psi }_{{||}}})}}^{2}} - \chi _{0}^{'}} \right)}}^{2}}}}R_{{{\text{ПРИВ}}}}^{{(s)}}, \\ \end{gathered} $(9в)
$R_{1}^{{(s)}} = \frac{1}{{{{\Delta }^{{(s)}}}}}\frac{{{{{\sin }}^{2}}\left( {{{{{b}^{{(s)}}}\Delta _{1}^{{(s)}}} \mathord{\left/ {\vphantom {{{{b}^{{(s)}}}\Delta _{1}^{{(s)}}} 2}} \right. \kern-0em} 2}} \right)}}{{\Delta {{{_{1}^{{(s)}}}}^{2}}}},$(9г)
$R_{2}^{{(s)}} = \frac{1}{{{{\Delta }^{{(s)}}}}}\frac{{{{{\sin }}^{2}}\left( {{{{{b}^{{(s)}}}\Delta _{2}^{{(s)}}} \mathord{\left/ {\vphantom {{{{b}^{{(s)}}}\Delta _{2}^{{(s)}}} 2}} \right. \kern-0em} 2}} \right)}}{{\Delta {{{_{2}^{{(s)}}}}^{2}}}},$(9д)
$R_{{{\text{ИНТ}}}}^{{(s)}} = \frac{{ - 1}}{{{{\Delta }^{{(s)}}}}}\frac{{\cos \left( {{{b}^{{(s)}}}{{\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \mathord{\left/ {\vphantom {{\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \varepsilon }} \right. \kern-0em} \varepsilon }} \right)\left[ {\cos \left( {{{b}^{{(s)}}}{{\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \mathord{\left/ {\vphantom {{\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \varepsilon }} \right. \kern-0em} \varepsilon }} \right) - \cos \left( {{{b}^{{(s)}}}\left( {{{\sigma }^{{(s)}}} - {{{{\xi }^{{(s)}}}} \mathord{\left/ {\vphantom {{{{\xi }^{{(s)}}}} \varepsilon }} \right. \kern-0em} \varepsilon }} \right)} \right)} \right]}}{{\Delta _{1}^{{(s)}}\Delta _{2}^{{(s)}}}},$(10)
$\begin{gathered} {{\Omega }^{{(1)}}} = {{\theta }_{ \bot }} - {{\psi }_{ \bot }},\,\,\,\,{{\Omega }^{{(2)}}} = {{\theta }_{{||}}} - {{\psi }_{{||}}}, \\ \Delta _{{1,2}}^{{(s)}}\left( \eta \right) = {{\sigma }^{{(s)}}} - \frac{{{{\xi }^{{(s)}}} \mp \,\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } }}{\varepsilon }, \\ {{\Delta }^{{(s)}}}(\eta ) = {{\xi }^{{(s)}}}^{2} - \varepsilon + \varepsilon {{\sin }^{2}}\frac{{{{b}^{{(s)}}}\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } }}{\varepsilon }, \\ {{\xi }^{{(s)}}}\left( \omega \right) = {{\eta }^{{(s)}}}(\omega ) + \frac{{1 + \varepsilon }}{{2{{\nu }^{{(s)}}}}}\,, \\ {{\eta }^{{(s)}}}(\omega ) = \frac{{2{{\pi }^{2}}{{n}^{2}}}}{{{{T}^{2}}{{\omega }_{{\text{B}}}}}}L_{{{\text{ext}}}}^{{(s)}}\left( {1 - \frac{\omega }{{{{\omega }_{{\text{B}}}}}}\left( {1 + {{\theta }_{\parallel }}\sqrt {\frac{{{{T}^{2}}\omega _{{\text{B}}}^{2}}}{{{{\pi }^{2}}{{n}^{2}}}} - 1} } \right)} \right), \\ {{b}^{{(s)}}} = \frac{{{{L}_{e}}}}{{2L_{{{\text{ext}}}}^{{(s)}}}},\,\,\,\,{{L}_{e}} = \frac{L}{{\sin ({{\theta }_{{\text{B}}}} + \delta )}}, \\ L_{{{\text{ext}}}}^{{(s)}} = \frac{1}{\omega }\frac{{\pi n}}{{\left| {\sin \left( {\frac{{\pi n}}{{1 + r}}} \right)} \right|\left| {\chi _{2}^{'} - \chi _{1}^{'}} \right|{{C}^{{(s)}}}}},\,\,\,\,{{\omega }_{{\text{B}}}} = \frac{{\pi \,n}}{{T\sin {{\theta }_{{\text{B}}}}}}, \\ \varepsilon = \frac{{\sin ({{\theta }_{{\text{B}}}} - \delta )}}{{\sin ({{\theta }_{{\text{B}}}} + \delta )}},\,\,\,\,{{\sigma }^{{(s)}}} = \frac{{\pi n}}{{{{C}^{{(s)}}}\left| {\chi _{2}^{'} - \chi _{1}^{'}} \right|\left| {\sin \left( {\frac{{\pi n}}{{1 + r}}} \right)} \right|}} \times \\ \times \,\,\left( {{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{\parallel }} + {{\psi }_{\parallel }})}}^{2}} - \chi _{0}^{'}} \right), \\ {{\nu }^{{(s)}}} = \frac{{{{C}^{{(s)}}}\left| {\sin \left( {\frac{{\pi n}}{{1 + r}}} \right)} \right|}}{{\frac{{\pi n}}{{1 + r}}}}\left| {\frac{{\chi _{2}^{'} - \chi _{1}^{'}}}{{\chi _{1}^{'} + r\chi _{2}^{'}}}} \right|, \\ \chi _{0}^{'} = \frac{{\chi _{1}^{'} + r\chi _{2}^{'}}}{{1 + r}},\,\,\,\,r = \frac{{{{l}_{2}}}}{{{{l}_{1}}}}. \\ \end{gathered} $Так как в области рентгеновских частот выполняется неравенство $2{{\pi }^{2}}{{n}^{2}}L_{{{\text{ext}}}}^{{(s)}}{\text{/}}{{T}^{2}}{{\omega }_{{\text{B}}}} \gg 1,$ то ${{\eta }^{{(s)}}}(\omega )$ является быстрой функцией от частоты $\omega $, поэтому для дальнейшего анализа спектров ПРИВ и ПИ очень удобно рассматривать ${{\eta }^{{(s)}}}(\omega )$ или ${{\xi }^{{(s)}}}\left( \omega \right)$ как спектральную переменную, характеризующую частоту $\omega {\text{.}}$
Для фиксированного значения ${{\theta }_{{\text{B}}}}$ параметр асимметрии $\varepsilon $ определяет ориентацию входной поверхности мишени относительно отражающих слоев.
При уменьшении угла падения $\left( {{{\theta }_{{\text{B}}}} + \delta } \right)$ электрона на мишень параметр $\delta $ становится отрицательным и далее возрастает по модулю (в предельном случае $\delta \to - {{\theta }_{{\text{B}}}}$), что приводит и к возрастанию $\varepsilon .$ Напротив, при увеличении угла падения $\varepsilon $ убывает (предельный случай $\delta \to {{\theta }_{{\text{B}}}}$). В случае симметричного отражения, когда $\delta = 0{\text{,}}$ параметр асимметрии $\varepsilon = 1.$ На рис. 1 указано положительное направление угла $\delta .$
Параметр ${{\nu }^{{(s)}}},$ принимающий значения в промежутке $0 \leqslant {{\nu }^{{(s)}}} \leqslant 1,$ определяет степень отражения поля электрона слоев мишени, которая обусловливается характером интерференции волн, отраженных от разных слоев: конструктивным (${{\nu }^{{(s)}}} \approx 1$) или деструктивным (${{\nu }^{{(s)}}} \approx 0$).
Спектральная функция $R_{{{\text{ПРИВ}}}}^{{(s)}}$ (9б) представлена в виде слагаемых, описывающих вклады в спектр ПРИВ двух ветвей рентгеновских волн $R_{{}}^{{(1)}}$ и ${{R}^{{(2)}}},$ а также их интерференционного слагаемого $R_{{{\text{ИНТ}}}}^{{(s)}}.$ Каждой рентгеновской волне соответствуют волновые векторы, длины которых имеют вид:
(11)
$\begin{gathered} {{k}^{{(1,2)}}} = \omega \sqrt {1 + \chi _{0}^{'}} + \omega \frac{{{{C}^{{(s)}}}\left| {\chi _{2}^{'} - \chi _{1}^{'}} \right|\left| {\sin \left( {\frac{{\pi n}}{{1 + r}}} \right)} \right|}}{{2\pi n\varepsilon }} \times \\ \times \,\,\left( {{{\xi }^{{(s)}}}\left( \omega \right) \mp } \right.\left. {\sqrt {{{\xi }^{{(s)}}}{{{\left( \omega \right)}}^{2}} - \varepsilon } } \right). \\ \end{gathered} $Вклад первой $R_{{}}^{{(1)}}$ и вклад второй $R_{{}}^{{(2)}}$ ветви ПРИВ будут существенны, когда имеют решения соответствующие уравнения:
(12a)
${{\sigma }^{{(s)}}} - \frac{{{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } }}{\varepsilon } = 0,$(12б)
${{\sigma }^{{(s)}}} - \frac{{{{\xi }^{{(s)}}} + \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } }}{\varepsilon } = 0.$(13)
$\begin{gathered} - \sqrt \varepsilon < {{\xi }^{{(s)}}}(\omega ) < \sqrt \varepsilon , \\ - \sqrt \varepsilon - {{(1 + \varepsilon )} \mathord{\left/ {\vphantom {{(1 + \varepsilon )} {2{{\nu }^{{(s)}}}}}} \right. \kern-0em} {2{{\nu }^{{(s)}}}}} < {{\eta }^{{(s)}}}(\omega ) < \\ < \sqrt \varepsilon - {{(1 + \varepsilon )} \mathord{\left/ {\vphantom {{(1 + \varepsilon )} {2{{\nu }^{{(s)}}}}}} \right. \kern-0em} {2{{\nu }^{{(s)}}}}}, \\ \end{gathered} $Получено выражение, описывающее спектрально-угловую плотность переходного излучения:
(14а)
$\omega \frac{{{{d}^{2}}N_{{{\text{ПИ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}{{\Omega }^{{(s)}}}^{2}\left( {\frac{1}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} - {{\psi }_{{||}}})}}^{2}}}}} \right. - {{\left. {\frac{1}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} - {{\psi }_{{||}}})}}^{2}} - \chi _{0}^{'}}}} \right)}^{2}}R_{{{\text{ПИ}}}}^{{(s)}},$(14б)
$R_{{{\text{ПИ}}}}^{{(s)}} = 1 + \frac{{{{\xi }^{{(s)}}}^{2} - \varepsilon }}{{{{\Delta }^{{(s)}}}(\eta )}}\left[ {1 - \frac{1}{{\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } }}\left( {\left( {{{\xi }^{{(s)}}} + \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \right)} \right.\cos \left( {{{b}^{{(s)}}}\Delta _{1}^{{(s)}}\left( \eta \right)} \right)\left. { - \left( {{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \right)\cos \left( {{{b}^{{(s)}}}\Delta _{2}^{{(s)}}\left( \eta \right)} \right)} \right)} \right].$Выражение (14) справедливо для всех возможных значений величин ${{\xi }^{{(s)}}}\left( \omega \right)$ и существенно отличается от формулы для ПИ из аморфной пластины той же толщины L. Это отличие вызвано эффектами динамической дифракции. Оно является значительным только в окрестности Брэгговской частоты $\left| {{{\xi }^{{(s)}}}\left( \omega \right)} \right| \leqslant {{\varepsilon }^{{1/2}}}.$ Вне окрестности $\left| {{{\xi }^{{(s)}}}\left( \omega \right)} \right| \gg {{\varepsilon }^{{1/2}}}$ спектральная функция принимает вид хорошо известного выражения для ПИ, в аморфной диэлектрической пластинки:
Из выражения (15) следует, что деструктивная интерференция волн ПИ, испущенных из входной и выходной поверхности мишени, будет полностью подавлять частоты далекие от частоты Брэгга при резонансном условии:(16)
${{b}^{{(s)}}}{{\sigma }^{{(s)}}} = 2\pi m,\,\,\,m - {\text{натуральное}}\,\,{\text{число}}{\text{.}}$(17а)
$\begin{gathered} \omega \frac{{{{d}^{2}}N_{{{\text{ИНТ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \\ = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}{{\Omega }^{{(s)}}}^{2}\frac{1}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} - {{\psi }_{{||}}})}}^{2}} - \chi _{0}^{'}}} \times \\ \times \,\,\left( {\frac{1}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} - {{\psi }_{{||}}})}}^{2}} - \chi _{0}^{'}}}} \right. - \\ - \,\,\left. {\frac{1}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} - {{\psi }_{{||}}})}}^{2}}}}} \right)R_{{{\text{ИНТ}}}}^{{(s)}}, \\ \end{gathered} $(17б)
$R_{{{\text{ИНТ}}}}^{{(s)}} = \frac{1}{{2{{\Delta }^{{(s)}}}(\eta )}}\left[ {R_{{{\text{ПРИВ1,ПИ}}}}^{{(s)}} - R_{{{\text{ПРИВ2,ПИ}}}}^{{(s)}}} \right],$(17в)
$\begin{gathered} R_{{{\text{ПРИВ1,ПИ}}}}^{{(s)}} = \frac{1}{{\Delta _{1}^{{(s)}}\left( \eta \right)}}\left[ {2\left( {3\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } + {{\xi }^{{(s)}}}} \right)} \right. \times \\ \times \,\,{{\sin }^{2}}\left( {\frac{{{{b}^{{(s)}}}\Delta _{1}^{{(s)}}\left( \eta \right)}}{2}} \right) + \left( {{{\xi }^{{(s)}}} - \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \right) \times \\ \left. { \times \,\,\left( {\cos \left( {{{2{{b}^{{(s)}}}\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \mathord{\left/ {\vphantom {{2{{b}^{{(s)}}}\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \varepsilon }} \right. \kern-0em} \varepsilon }} \right) + \cos \left( {{{b}^{{(s)}}}\Delta _{2}^{{(s)}}\left( \eta \right)} \right)} \right)} \right], \\ \end{gathered} $(17г)
$\begin{gathered} R_{{{\text{ПРИВ2,ПИ}}}}^{{(s)}} = \frac{1}{{\Delta _{2}^{{(s)}}\left( \eta \right)}}\left[ {2\left( {3\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } - {{\xi }^{{(s)}}}} \right)} \right. \times \\ \times \,\,{{\sin }^{2}}\left( {\frac{{{{b}^{{(s)}}}\Delta _{2}^{{(s)}}\left( \eta \right)}}{2}} \right) + \left( {{{\xi }^{{(s)}}} + \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \right) \times \\ \left. { \times \,\,\left( {\cos \left( {{{2{{b}^{{(s)}}}\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \mathord{\left/ {\vphantom {{2{{b}^{{(s)}}}\sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \varepsilon }} \right. \kern-0em} \varepsilon }} \right) - \cos \left( {{{b}^{{(s)}}}\Delta _{1}^{{(s)}}\left( \eta \right)} \right)} \right)} \right]. \\ \end{gathered} $Выражения (9), (14) и (17), описывающие вклады в спектрально угловую плотность излучения релятивистского электрона ПРИВ, ПИ и их интерференционного слагаемого с учетом отклонения направления скорости электрона ${\mathbf{V}}$ от направления оси электронного пучка ${{{\mathbf{e}}}_{1}},$ заданного углом $\psi ({{\psi }_{ \bot }},{{\psi }_{\parallel }}),$ представляют главный результат настоящей работы. Эти выражения получены для общего случая асимметричного отражения поля электрона относительно поверхности мишени и содержат зависимость от коэффициента асимметрии $\varepsilon .$
ЧИСЛЕННЫЕ РАСЧЕТЫ И АНАЛИЗ СПЕКТРАЛЬНО-УГЛОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЙ
Используя полученные выражения (9), (14) и (17) проведем численные расчеты для различных параметров и проанализируем свойства когерентного рентгеновского излучения, а также возможность для наблюдения ПРИВ релятивистских электронов, генерируемое в периодической слоистой среде. Для определенности рассмотрим когерентное излучение в периодической слоистой среде, состоящей из слоев с диэлектрическими восприимчивостями $\chi _{1}^{'} \approx {{10}^{{ - 4}}}$ и $\chi _{2}^{'} \approx {{10}^{{ - 5}}},$ вблизи окрестности частоты Брэгга ${{\omega }_{B}}$. Вычисления спектрально-угловой плотности когерентного рентгеновского излучения проведем для $\sigma $−поляризованных волн ($s = 1$), первой гармоники $n = 1.$ Отклонение направлении скорости электрона в пучке от оси пучка будем считать равной нулю $\psi = 0$ (${{\psi }_{ \bot }} = {{\psi }_{\parallel }} = 0$). Толщины отражающий слоев одинаковы $r = {{l}_{2}}{\text{/}}{{l}_{1}} = 1,$ при этом средняя диэлектрическая восприимчивость в мишени $\chi _{0}^{'} = $ $ = - 5.5 \times {{10}^{{ - 5}}}.$
Будем рассматривать случай, когда выполняется неравенство $\varepsilon > 1{\text{/}}{{\sigma }^{{(s)}}}^{2},$ то есть вклад будет давать только вторая ветвь ПРИВ. Численные расчеты показывают, что при рассматриваемых нами параметрах выполняется неравенство ${{\sigma }^{{(s)}}} > 2,$ при этом минимальный параметр асимметрии при котором отсутствует первая ветвь ПРИВ: $\varepsilon = 0.25.$ Необходимо отметить, что в случае $\varepsilon < 0.25,$ при рассматриваемых параметрах, спектрально-угловая плотность второй ветви ПРИВ будет существенно превышать спектрально-угловую плотность первой ветви. Запишем выражение, описывающее спектрально-угловую плотность второй ветви ПРИВ (9а) и (9г) для $\sigma $-поляризованных волн при ${{\psi }_{ \bot }} = {{\psi }_{\parallel }} = 0$:
(18а)
$\omega \frac{{{{d}^{2}}N_{{{\text{ПРИВ}}}}^{{(1)}}}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{{\theta _{ \bot }^{2}}}{{{{{\left( {{{\gamma }^{{ - 2}}} + \theta _{ \bot }^{2} + \theta _{\parallel }^{2} - \chi _{0}^{'}} \right)}}^{2}}}}R_{2}^{{(1)}},\,$(18б)
$\begin{gathered} R_{2}^{{(1)}} = \frac{1}{{{{\xi }^{{(1)}}}^{2} - \varepsilon + \varepsilon {{{\sin }}^{2}}\frac{{{{b}^{{(1)}}}\sqrt {{{\xi }^{{(1)}}}^{2} - \varepsilon } }}{\varepsilon }}} \times \\ \times \,\,\frac{{{{{\sin }}^{2}}\left( {\frac{{{{b}^{{(1)}}}}}{2}\left( {{{\sigma }^{{(1)}}} - \frac{{{{\xi }^{{(1)}}} + \sqrt {{{\xi }^{{(1)}}}^{2} - \varepsilon } }}{\varepsilon }} \right)} \right)}}{{{{{\left( {{{\sigma }^{{(1)}}} - \frac{{{{\xi }^{{(1)}}} + \sqrt {{{\xi }^{{(1)}}}^{2} - \varepsilon } }}{\varepsilon }} \right)}}^{2}}}}. \\ \end{gathered} $Рассмотрим зависимость спектрально-угловой плотности ПРИВ релятивистского электрона от угла наблюдения ${{\theta }_{ \bot }}{\text{,}}$ при этом будем полагать ${{\theta }_{\parallel }} = 0.$ На рис. 2 представлены кривые, построенные по формуле (18а), описывающие спектрально-угловые плотности ПРИВ при различных углах наблюдения, для $\gamma = 200.$ Функция, описывающая угловую часть ПРИВ: ${{F}^{{(1)}}} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}} \times $ $ \times \,\,\frac{{\theta _{ \bot }^{2}}}{{{{{\left( {{{\gamma }^{{ - 2}}} + \theta _{ \bot }^{2} + \theta _{\parallel }^{2} - \chi _{0}^{'}} \right)}}^{2}}}},$ имеет максимум в точке ${{\theta }_{ \bot }} = \sqrt {{{\gamma }^{{ - 2}}} - \chi _{0}^{'}} .$ Для рассматриваемых параметров $\chi _{0}^{'} = - 5.5 \times {{10}^{{ - 5}}}$ и $\gamma = 200,$ этот угол равен ${{\theta }_{ \bot }} \approx $ $ \approx 9$ мрад, что и демонстрирует кривая, приведенная на рис. 3. Однако, угол максимума спектрально-угловой плотности ПРИВ, в рассматриваемом случае, имеет значение $\theta _{ \bot }^{{\max }} \approx 6$ мрад (рис. 2). Это связано с тем, что максимум динамической спектральной функции $R_{2}^{{(1)}}$ увеличивается с уменьшением угла наблюдения ${{\theta }_{ \bot }},$ данный эффект демонстрируют кривые, представленные на рис. 4. Важно отметить, что кинематическая теории ПРИ, не предсказывает пик ПРИВ.
Рис. 2.
Спектрально-угловая плотность ПРИВ. Параметры: ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ ${{b}^{{(s)}}} = 10,$ $\varepsilon = 1.$
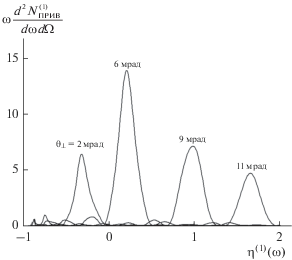
Рис. 3.
Угловая часть спектрально-угловой плотности ПРИВ. Параметры: ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ ${{b}^{{(s)}}} = 10,$ $\varepsilon = 1.$
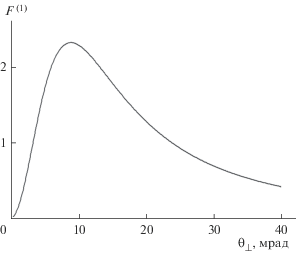
Рис. 4.
Спектр ПРИВ. Параметры: ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ ${{b}^{{(s)}}} = 10,$ $\varepsilon = 1.$

На рис. 5 представлены кривые, демонстрирующие рост спектрально угловой плотности ПРИВ при увеличении пути электрона в мишени b(1) = $ = {{L}_{e}}{\text{/}}2L_{{{\text{ext}}}}^{{(1)}},$ выраженной в двойной длине экстинкции.
Рис. 5.
Спектрально-угловая плотность ПРИВ при различном пути электрона в мишени. Параметры: ${{{\theta }}_{ \bot }} = 6$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ $\varepsilon = 1.$

Полученное выражение (18а) $1$предсказывает влияние асимметрии отражения поля электрона относительно поверхности мишени на спектрально-угловую плотность излучения. Рассмотрим зависимость спектрально-угловой плотности ПРИВ при фиксированном угле наблюдения от асимметрии отражения. Кривые, построенные по формулам (18а) и представленные на рис. 6, демонстрируют рост амплитуды спектрально-угловой плотности ПРИВ с уменьшением параметра асимметрии $\varepsilon {\text{,}}$ при этом ширина спектра уменьшается. Например: $\varepsilon = 0.5$ (при ${{{\theta }}_{{\text{B}}}}{\text{ = 10}}^\circ $ и $\delta = 3.4^\circ $), $\varepsilon = 1.5$ (при ${{{\theta }}_{{\text{B}}}} = 10^\circ $ и $\delta = - 2^\circ $). Случай симметричного отражения соответствует $\varepsilon = 1\,\,{\text{(}}\delta = 0{\text{)}}.$
Рис. 6.
Влияние асимметрии отражения на спектрально-угловую плотность ПРИВ при фиксированном угле наблюдения. Параметры: ${{{\theta }}_{ \bot }} = 6$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ ${{b}^{{(s)}}} = 10.$

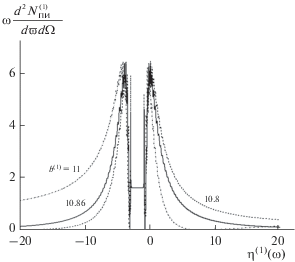
Ввиду того, что переходное излучение будет являться фоном при экспериментальной регистрации ПРИВ и исследовании его свойств, то необходимо проанализировать спектрально-угловую плотность ПИ и влияние вклада интерференции ПРИВ и ПИ в когерентное рентгеновское излучение. На рис. 7 представлены кривые, построенные по формуле (14а), описывающие спектрально-угловую плотность переходного излучения при фиксированном угле наблюдения. Кривые построены при различных значениях параметра b(1) = $ = {{L}_{e}}{\text{/}}2L_{{{\text{ext}}}}^{{(1)}}.$ Сплошная кривая на рис. 7, построенная при параметре ${{b}^{{(1)}}} = 10.86,$ соответствует резонансному условию (16), при $m = 7.$ Из рисунка видно, что небольшое увеличение параметра ${{b}^{{(1)}}}$ (пути электрона в мишени) приводит к уменьшению спектрально-угловой плотности ПИ справа и увеличению ее слева, что может быль полезно при экспериментальной идентификации пика ПРИВ.
Рис. 7.
Спектрально-угловая плотность ПИ при различных ${{b}^{{(1)}}}.$ Параметры: ${{{\theta }}_{ \bot }} = 6$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ $\varepsilon = 1.$
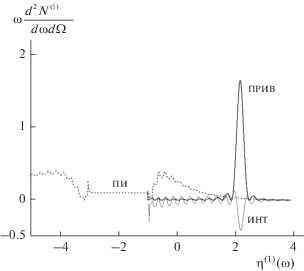
В некоторых случаях существенной может быть деструктивная интерференция волн ПРИВ и ПИ. На рис. 8 представлены кривые, построенные по формулам (18а), (14а) и (17а), описывающие спектрально-угловые плотности ПРИВ, ПИ и их интерференцию. Из рисунка следует, что хотя условие подавления фона переходного излучения вдали от частоты Брэгга ${{{\omega }}_{{\text{B}}}}$ (${{{\eta }}^{{{\text{(1)}}}}} = {\text{0}}$) выполняется, однако существенна деструктивная интерференция волн ПРИВ и ПИ, что может затруднить экспериментальную регистрацию ПРИВ в этих условиях.
Рис. 8.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция. Параметры: ${{{\theta }}_{ \bot }} = 6$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ ${{b}^{{(1)}}} = 11.$

На рис. 9 представлены кривые, аналогичные кривым рис. 8, но при ${{b}^{{(1)}}} = 10.$ Из рис. 9 следует конструктивная интерференция волн ПРИВ и ПИ, хотя волны ПИ, имеющие частоты далекие от частоты Брэгга, не подавляются.
На рис. 10 представлены кривые аналогичные кривым рис. 8, но в асимметричном случае, при $\varepsilon = 0.5.$ Из рисунка следует многократное увеличение спектрально-угловой плотности ПРИВ (по сравнению с рис. 8).
Рис. 10.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция. Параметры: ${{{\theta }}_{ \bot }} = 6$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 200,$ ${{b}^{{(1)}}} = 11,$ $\varepsilon = 0.5.$

Рассмотрим спектрально-угловую плотность излучений в случае меньшей энергии релятивистских электронов (при $\gamma = 100$). Угол максимума спектрально-угловой плотности ПРИВ в рассматриваемом случае имеет значение $\theta _{ \bot }^{{\max }} \approx 9$ мрад. На рис. 11, 12 построены кривые, описывающие спектрально-угловые плотности ПРИВ, ПИ и их интерференцию. На рис. 11 кривые построены в случае в основном конструктивной интерференции ПРИВ и ПИ. На рис. 12 интерференция ПРИВ и ПИ деструктивна, однако фон переходного излучения в области пика ПРИВ очень мал. Этот фон подавлен за счет деструктивной интерференции волн переходного излучения из передней и задней границы, то есть выполняется условие (16). Необходимо отметить, существенное уменьшение амплитуды пика ПРИВ при $\gamma = 100,$ по сравнению с $\gamma = 200{\text{,}}$ однако фон переходного излучения уменьшается еще больше.
Рис. 11.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция. Параметры: ${{{\theta }}_{ \bot }} = 9$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 100,$ ${{b}^{{(1)}}} = 10.2,$ $\varepsilon = 1.$

Рассмотрим спектрально-угловую плотность излучений в случае меньшей энергии релятивистских электронов, при $\gamma = 50.$ Угол максимума спектрально-угловой плотности ПРИВ в этом случае $\theta _{ \bot }^{{\max }} \approx 12$ мрад. Из рис. 13 и 14 следует, как и ожидалось, еще большее уменьшениe фона переходного излучения, относительно амплитуды пика ПРИВ.
Рис. 13.
Спектрально-угловые плотности ПРИВ, ПИ и их интерференция. Параметры: ${{{\theta }}_{ \bot }} = 12$ мрад, ${{{\theta }}_{\parallel }} = 0,$ $\gamma = 50,$ ${{b}^{{(1)}}} = 10,$ $\varepsilon = 1.$

Если это необходимо, то формулы (9), (14) и (17) позволяют провести их усреднение по всем возможным прямолинейным траекториям электронов в пучке. Например, в случае распределения Гаусса электронов в пучке: $f(\psi ) = \frac{1}{{\pi \psi _{0}^{2}}} \times $ $ \times \,\,\exp \left( { - \frac{{\psi _{ \bot }^{2} + \psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}} \right),$ усреднение спектрально-угловых плотностей будет иметь вид
(19)
$\begin{gathered} \left\langle {\omega \frac{{{{d}^{2}}N_{{{\text{ПРИВ,ПИ,ИНТ}}}}^{{(1)}}}}{{d\omega d\Omega }}} \right\rangle = \frac{1}{{\pi \psi _{0}^{2}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\omega \frac{{{{d}^{2}}N_{{ПРИВ,ПИ,ИНТ}}^{{(1)}}}}{{d\omega d\Omega }}} } \times \\ \times \,\,\exp \left( { - \,\frac{{\psi _{ \bot }^{2} + \psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}} \right)d{{\psi }_{ \bot }}d{{\psi }_{\parallel }}. \\ \end{gathered} $С целью учета многократного рассеяния излучающих электронов в среде можно провести усреднение спектрально-угловых плотностей излучений по угловому распределения электронов в пучке в виде функции Гаусса, меняющейся с длиной пути прохождения в мишени $t$ за счет многократного рассеяния электрона:
(20)
$f(\psi ,t) = \frac{1}{{\pi \left( {\psi _{0}^{2} + \psi _{s}^{2}t} \right)}}\exp \left( { - \frac{{\psi _{ \bot }^{2} + \psi _{\parallel }^{2}}}{{\psi _{0}^{2} + \psi _{s}^{2}t}}} \right),$(21)
$\begin{gathered} \left\langle {\omega \frac{{{{d}^{2}}N_{{ПРИВ,ПИ,ИНТ}}^{{(1)}}}}{{d\omega d\Omega }}} \right\rangle = \\ = \frac{1}{{\pi {{L}_{e}}}}\int\limits_0^{{{L}_{e}}} {dt\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {d{{\psi }_{ \bot }}d{{\psi }_{\parallel }}\frac{{\exp \left( { - \frac{{\psi _{ \bot }^{2} + \psi _{\parallel }^{2}}}{{\psi _{0}^{2} + \psi _{s}^{2}t}}} \right)}}{{\psi _{0}^{2} + \psi _{s}^{2}t}}} } } \times \\ \times \,\,\omega \frac{{{{d}^{2}}N_{{ПРИВ,ПИ,ИНТ}}^{{(1)}}}}{{d\omega d\Omega }}. \\ \end{gathered} $ЗАКЛЮЧЕНИЕ
Развита динамическая теория когерентного рентгеновского излучения, возбуждаемого в периодической слоистой среде пучком релятивистских электронов в направлении, близком к оси пучка. Процесс излучения рассмотрен в геометрии рассеяния Брэгга для общего случая асимметричного отражения поля электрона относительно поверхности мишени. На основе двухволнового приближения динамической теории дифракции получены выражения, описывающие спектрально-угловые плотности ПРИВ, ПИ и интерференционное слагаемое. Показана возможность наблюдения ПРИВ. Показано, что интерференция ПРИВ и ПИ может быть, как конструктивной, так и деструктивной. Уменьшение параметра асимметрии $\varepsilon $ может привести к существенному росту амплитуды спектрально-угловой плотности ПРИВ. Уменьшение энергии излучающих электронов приводит к уменьшению амплитуды спектрально-угловой плотности ПРИВ, однако положительным моментом является существенное уменьшение фона переходного излучение в этом случае.
Проведенный анализ и полученные в настоящей работе выражения для спектрально-угловых плотностей ПРИВ, ПИ (и их интерференции) можно использовать для определения оптимальных параметров эксперимента по регистрации ПРИВ-пучка релятивистских электронов, пересекающих мишень из периодической слоистой среды.
Список литературы
Nabokov N.N., Kaplan V.V., Uglov S.R., Pietro M.A., Gary C.K. // Phys. Rev E. 2003. V. 68. P. 3604.
Гарибян Г.М., Ян Ши // ЖЭТФ. 1971. Т. 61. С. 930.
Барышевский В.Г., Феранчук И.Д. // ЖЭТФ. 1971. Т. 61. С. 944.
Baryshevsky V.G. // Nucl. Instrum. Methods Phys. Res., A. 1997. V. 122. P. 13
Artru X., Rullhusen P. // Nucl. Instrum. Methods Phys. Res., B. 1998. V. 145. P. 1.
Nasonov N.N. // Phys. Lett. A. 1998. V. 246. P. 148.
Kaplin V.V., Uglov S.R., Zabaev V.N., Piestrup M.A., Gary C.K., Nasonov N.N., Fuller M. K. // Appl. Phys. Lett. 2000. V. 76. P. 3647.
Блажевич С.В., Гладких Ю.П., Носков А.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2013. № 4. С. 99.
Блажевич С.В., Носков А.В. // ЖЭТФ. 2017. Т. 152. С. 267.
Блажевич С.В., Гладких Ю.П., Носков А.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2014. № 12. С. 91.
Гарибян Г.М., Ян Ши // ЖЭТФ. 1972. Т. 63. С. 1198.
Caticha A. // Phys. Rev. B. 1992. V. 45. P. 9541.
Блажевич С. В., Носков А.В. // ЖЭТФ. 2009. V. 136. P. 1043.
Nasonov N., Noskov A. // Nucl. Instrum. Methods Phys. Res., B. 2003. V. 201. P. 67.
Алейник А.Н., Балдин А.Н., Богомазова Е.А., Внуков И.Е. и др. // Письма в ЖЭТФ. 2004. V. 80. P. 447.
Базылев В.А., Жеваго Н.К. Излучение быстрых частиц в веществе и внешних полях. М.: Наука, 1987. 272 с.
Partic1e Data Group, R. M. Barnett et al. // Phys. Rev. D. 1996. V. 54. P. 1.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования