Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 6, стр. 35-42

ВВЕДЕНИЕ

Расходимость электронного пучка и его поперечные размеры являются одними из наиболее важных параметров любого ускорителя. Для их измерения разработано большое количество разнообразных методик, включая использование проволочных сканеров [1, 2] и флуоресцентных экранов. На ускорителях электронов широко используется оптическое излучение, возникающее при пролете частиц через тонкие металлические пластины или около них, соответственно оптическое переходное излучение (ОПИ) [3] и оптическое дифракционное излучение (ОДИ) [4]. Однако, как было недавно показано, ОПИ нельзя использовать для измерения профиля электронных пучков линейных ускорителей, используемых для создания рентгеновского лазера на свободных электронах (ЛСЭ, поскольку ОПИ становится когерентным, когда продольный размер электронного сгустка сопоставим с длиной волны регистрируемого излучения [5].

Избежать эффекта когерентности можно за счет использования излучения с длиной волны меньше характерных размеров банча, в частности, параметрического рентгеновского излучения (ПРИ) электронов в кристаллах [6, 7]. Измерения угловых распределений ПРИ быстрых электронов в тонких кристаллах с помощью координатных детекторов [7–9] подтвердили возможность определения размеров пучка детектором, расположенным в непосредственной близости от кристалла [7], изменения формы регистрируемых распределений в зависимости от размера пучка на кристалле [8]. Возможность определения размеров пучка частиц на мишени с помощью камеры-обскуры также была показана в работе [9].

Расположение координатного детектора в непосредственной близости от источника излучения [7] не всегда возможно. К тому же, возникает проблема отделения регистрируемого углового распределения от фона тормозного излучения, источником которого являются элементы конструкции ускорителя. Использование камеры-обскуры [9] требует значительного времени для проведения измерений из-за жесткой коллимации излучения и предполагает азимутальную симметрию углового распределения регистрируемого излучения. Как отмечено в цитируемой работе, невыполнение этого условия приводит к систематической ошибке результатов измерений размеров пучка электронов на мишени.

В работе [10] на основе подхода [11] развита методика учета влияния поперечных размеров пучка частиц на мишени на регистрируемое угловое распределение для трех механизмов генерации когерентного излучения при взаимодействии быстрых электронов с кристаллами: ПРИ, дифрагированного тормозного излучения (ДТИ) и дифрагированного переходного излучения (ДПИ). Сопоставление результатов расчета с экспериментальными данными [12, 13] показало хорошее согласие и подтвердило адекватность развитой методики. Анализ, выполненный в цитируемой работе, показал, что измерение одномерных угловых распределений не в состоянии обеспечить требуемую точность определения размеров пучка частиц на кристалле из-за систематической ошибки, обусловленной взаимным влиянием размеров пучка в одной плоскости на результаты измерения углового распределения в другой.

Для решения этой проблемы предложено определять размер пучка электронов в обеих плоскостях по результатам измерений двумерных угловых распределений когерентного излучения электронов в тонком кристалле для двух расстояний между кристаллом, где генерируется регистрируемое излучение, и координатным детектором с помощью метода наименьших квадратов. Для доказательства работоспособности метода в цитируемой работе [10] использовалось модельное угловое распределение, близкое к угловому распределению ПРИ, но несовпадающее с ним, что не позволило достоверно определить границы чувствительности и область применимости метода.

Исходя из вышеизложенного, определение чувствительности предложенного метода и границ его применимости представляется важным и актуальным.

УЧЕТ ПРОСТРАНСТВЕННЫХ РАЗМЕРОВ ЭЛЕКТРОННОГО ПУЧКА

Приведем краткое описание методики оценки размера электронного пучка, следуя работе [10]. Влияние размеров пучка и расстояния между кристаллом и детектором на измеряемое двумерное угловое распределение когерентного излучения, например, [7], можно описать следующим выражением:

где $Y(\theta _{y}^{'},\theta _{x}^{'})$ и $Y\left( {{{\theta }_{y}},{{\theta }_{x}}} \right)$ угловые распределения когерентного излучения для протяженного и точечного пучка частиц на мишени, интегрирование ведется в пределах полного телесного угла. Функция $G({{\theta }_{y}} \to \theta _{y}^{{\text{'}}},{{\theta }_{x}} \to \theta _{x}^{{\text{'}}})$ описывает связь между переменными каждого из этих распределений в случае разброса точек попадания электронов на кристалл и для двумерного гауссовского распределения такого разброса может быть представлена в виде: где ${{\sigma }_{x}},$ $~{{\sigma }_{y}}\,\, - ~$характерные размеры пучка в горизонтальной и вертикальной плоскостях, а R − расстояние между кристаллом и детектором. Как видно из приведенных выражений, изменение расстояния между кристаллом и детектором приводит к изменению регистрируемого углового распределения излучения, что можно использовать для определения размера пучка путем сопоставления угловых распределений для разных расстояний между кристаллом и детектором.

Из-за неустранимой проблемы взаимовлияния размеров в обеих плоскостях на распределение интенсивности излучения в этих направлениях необходимо перейти к двумерным распределениям. Для детектора, расположенного на расстоянии R, измеряемое им двумерное распределение интенсивности излучения ${{Y}_{R}}\left( {{{\theta }_{{{{y}_{i}}}}},{{\theta }_{{{{x}_{j}}}}}} \right)$ исходя из выражения (1) можно записать в следующем виде:

где $Y(\theta _{y}^{{\text{'}}},\theta _{x}^{{\text{'}}})$ − свертка собственного углового распределения излучения с гауссовским распределением, параметры которого в соответствии с выражениями (1), (2), определяются размерами пучка и расстоянием между кристаллом и детектором. $\Delta {\Omega }\left( {{{y}_{i}},{{x}_{j}}} \right)~$ − телесный угол, перекрываемый элементом координатного детектора, расположенным в точке${\text{\;}}{{y}_{i}},$ ${{x}_{j}},$ по которому ведется интегрирование.

Очевидно, что различие распределений ${{Y}_{{{{R}_{1}}}}}(\theta _{{{{y}_{i}}}}^{{\text{'}}},$ $\theta _{{{{x}_{j}}}}^{{\text{'}}})$ и ${{Y}_{{{{R}_{2}}}}}(\theta _{{{{y}_{i}}}}^{{\text{'}}},\theta _{{{{x}_{j}}}}^{{\text{'}}}),$ измеренных для расстояний R₁ и R₂, обусловлено только характерными размерами пучка и расстояниями между кристаллом и детектором. А сами эти распределения являются результатами свертки углового распределения для точечного пучка частиц $Y\left( {{{\theta }_{y}},{{\theta }_{x}}} \right)$ и двух двумерных гауссовских распределений со стандартными отклонениями $\sigma _{{{{x}_{1}},{{y}_{1}}}}^{{\text{'}}} = {{{{\sigma }_{{x,y}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{x,y}}}} {{{R}_{1}}}}} \right. \kern-0em} {{{R}_{1}}}}$ и $\sigma _{{{{x}_{2}},{{y}_{2}}}}^{{\text{'}}} = {{{{\sigma }_{{x,{\text{y}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{x,{\text{y}}}}}} {{{R}_{2}}}}} \right. \kern-0em} {{{R}_{2}}}},$ где $~{{\sigma }_{{x,{\text{y}}}}}$ характерные размеры пучка на кристалле.

Считаем, что ${{R}_{1}} = k{{R}_{2}},$ где k − коэффициент, существенно отличающийся от единицы, а телесные углы, перекрываемые детекторами в каждом измерении, одинаковы. Таким образом, размеры элементов детектора для каждого из расстояний отличаются в k раз. В этом случае в первом приближении можно полагать, что ${{Y}_{{{{R}_{2}}}}}(\theta _{{{{y}_{i}}}}^{{\text{'}}},\theta _{{{{x}_{j}}}}^{{\text{'}}})$ является сверткой распределения ${{Y}_{{{{R}_{1}}}}}(\theta _{{{{y}_{i}}}}^{{\text{'}}},\theta _{{{{x}_{j}}}}^{{\text{'}}})$ с гауссовским распределением с дисперсией, зависящей от неизвестных нам размеров пучка на мишени и величин R₁, R₂.

Для определения искомых размеров пучка на мишени можно воспользоваться методом наименьших квадратов, минимизируя квадратичную форму:

где m и n − число точек измеряемого распределения в горизонтальном и вертикальном направлениях, а $\sigma _{x}^{{\text{'}}}$ и $\sigma _{y}^{{\text{'}}}$ − подгоночные параметры, минимизирующие эту форму, связаны с размерами пучка на мишени ${{\tilde {\sigma }}_{x}},$ ${{\tilde {\sigma }}_{y}}$ следующим образом:

С целью проверки методики и определения границ ее применимости проведено моделирование определения размеров пучка из двумерных распределений параметрического рентгеновского излучения с помощью вариации параметров свертки в комбинации с методом градиентного спуска. Моделирование выполнено для условий эксперимента [12]: кристалла кремния с отражающей плоскостью (011) и угла наблюдения 32.2°. Характерный угол вылета фотонов ПРИ Θ_ph = $ = \sqrt {{{\gamma }^{{ - 2}}} + \frac{{\omega _{p}^{2}}}{{{{\omega }^{2}}}}} = 3.32$ мрад, где $\gamma $ − Лоренц-фактор, $\omega = 11.65$ кэВ и ${{\omega }_{p}} = 30.8~$ эВ − энергия фотона и энергия плазмона среды. Энергия электронов 255 МэВ. Размер элементов детектора равен 0.1 мм и 0.2 мм в обоих направлениях для расстояний 0.5 и 1 м соответственно. Размер электронного пучка на кристалле − ${{\sigma }_{x}} = 0.3$ мм и ${{\sigma }_{y}} = 0.8$ мм. На рис. 1 приведено вертикальное (рис. 1а) и горизонтальное (рис. 1б) угловые распределения, проходящие через центр рефлекса. В качестве модельного распределения ПРИ (зависимость 1) использовалась формула Феранчука–Ивашина [14]:

Здесь ${{N}_{{PXR}}}\left( \omega \right)$ – множитель, который характеризует выход ПРИ, а ${{\Theta }_{{\text{B}}}}$ угол поворота плоскости кристалла относительно направления электронного пучка.

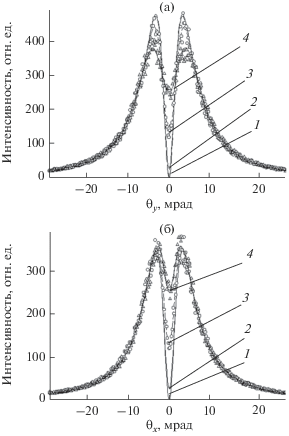
Для получения углового распределения от точечного пучка электронов (зависимость 2) угловое распределение ПРИ свертывалось с двумерным гауссовским распределением с ${{\theta }_{{\text{e}}}} = 0.3$ мрад, где ${{\theta }_{{\text{e}}}}$ − расходимость электронного пучка. Вклад дифракции реальных фотонов для этих условий не превышает 10% [11], и поэтому не учитывался. Зависимости 3 и 4 соответствуют протяженному электронному пучку для расстояний R₁= 2R₂= 1 м и R₂= 0.5 м. Для учета возможного влияния статистического разброса результатов измерений зависимости 3 и 4 “зашумлены” с помощью равномерного распределения в диапазоне значений ±10% в каждой точке, соответственно точки и треугольники.

Ошибка в определении параметров фитирования и оценки полученных из нее значений размера пучка не превышает нескольких процентов. Зависимость, полученная в результате подгонки, практически совпадает с зависимостью 4 и поэтому не приводится.

Для определения чувствительности метода и границ его применимости мы провели цикл оценок размера пучка, полученных с помощью этой методики, и “зашумленных” угловых распределений от расстояния между кристаллом и детектором. Моделирование выполнено для размеров пучка ${{\sigma }_{x}} = 0.3$ мм и ${{\sigma }_{y}} = 0.8$ мм. Остальные параметры совпадают с описанными выше. Полученная в результате подгонки зависимость оценки размера пучка ${{\tilde {\sigma }}_{{x,y}}}$ от расстояния приведена на рис. 2. В качестве ошибок мы взяли стандартное отклонение полученных в результате подгонки значений от среднего. Как и ранее полагаем условие R₁= 2R₂ выполненным.

Из рис. 2 видно, что для значений R₂ меньше полутора метров ошибка определения размера пучка не превышает 5−7%, а величины, полученные в результате подгонки, совпадают с использованными в моделировании. Однако для больших расстояний величина ${{\tilde {\sigma }}_{x}}$ отличается от истинного значения, тогда как значение ${{\tilde {\sigma }}_{y}},$ по-прежнему, совпадает с величиной, использованной в процессе моделирования, ${{\sigma }_{y}} = 0.8~$ мм.

Анализ показал, что причиной является уменьшение различий между зависимостями $~{{Y}_{1}}({{\theta }_{{{{y}_{i}}}}},{{\theta }_{{{{x}_{j}}}}})$ и ${{Y}_{2}}({{\theta }_{{{{y}_{i}}}}},{{\theta }_{{{{x}_{j}}}}})$ с ростом расстояния, поэтому для больших значений R₂ метод теряет чувствительность. Критерием отсутствия различий можно считать отношение величины $\sigma {\kern 1pt} ' = \frac{\sigma }{{{{R}_{2}}}}$ < 0.3 мрад к характерному углу ${{\Theta }_{{{\text{ph}}}}}$ = 3.32 мрад, то есть $\frac{{\sigma {\text{'}}}}{{{{\Theta }_{{{\text{ph}}}}}}} < 0.1.$

Полагая, что угол наблюдения и расстояние между кристаллом и детектором в эксперименте [8] близки к предельным значениям, мы можем оценить минимальный размер пучка, доступный для измерения с помощью предлагаемого метода. Расстояние между кристаллом и детектором, расположенным под углом 22.5°, было равно 350 мм. Для меньших расстояний и углов наблюдения расстояние между осью пучка и центром детектора будет меньше 10 см, что не позволит разместить в этой точке детектор вместе с защитой.

Отсюда, используя критерий $\sigma \sim 0.1R{{\Theta }_{{{\text{ph}}}}},$ где ${{\Theta }_{{{\text{ph}}}}} = 1.54$ мрад, получаем, что минимальный размер пучка, который можно оценить с помощью предлагаемой методики, составляет порядка 60 мкм.

Таким образом, методика, основанная на измерении угловых распределений ПРИ для двух расстояний, способна обеспечить измерение размера пучка ~100 мкм и выше, что типично для ускорителей средних энергий. Однако, она не применима для измерения поперечных размеров пучка порядка несколько десятков мкм в источниках излучения четвертого поколения [15], для которых и возникла проблема измерения пространственных размеров электронных банчей с малыми продольными размерами [5].

Как показано в работе [16] и подтверждено в [17, 18], с ростом энергии электронов до 5 ГэВ и выше вклад дифракции переходного излучения в центре рефлекса станет намного выше вклада ПРИ. Угловая плотность ДПИ для энергии электронов 10 ГэВ более чем в пятьсот раз превышает угловую плотность ПРИ из-за резкого уменьшения характерного угла излучения ${{\gamma }^{{ - 1}}},$ определяющего угловое распределение переходного излучения, а, следовательно, и ДПИ. Поэтому вклад ПРИ в центре углового распределения излучения может считаться пренебрежимо малым.

Присутствие яркого пика в угловом распределении излучения, близкого по форме к угловому распределению ПРИ [16, 23] и рис. 1, 3, позволяет использовать вышеописанную методику и для определения размера пучка электронов высоких энергий. В этом случае характерный угол выхода излучения близок к ${{\gamma }^{{ - 1}}},$ то есть оказывается в 10 и более раз меньше, чем ${{\Theta }_{{{\text{ph}}}}}{\text{,}}$ что обеспечивает примерно такое же уменьшение поперечного размера пучка электронов, которое можно измерить с помощью предлагаемой методики.

Для подтверждения вышесказанного на рис. 3 приведены результаты моделирования определения размера пучка электронов с энергией 10 ГэВ. Моделирование проведено для следующих условий: отражение (022) кристалла кремния, угол наблюдения 32.2°. Размер элемента детектора 10 × × 10 мкм для меньшего расстояния и 20 $ \times \,\,20$ мкм для большего. Размер пучка электронов на кристалле ${{\sigma }_{x}} = 15$ мкм и ${{\sigma }_{y}} = 20$ мкм. Расходимость электронного пучка ${{\theta }_{{\text{e}}}} = 15$ мкрад. Известно, например, [19, 20], что угловое распределение ДПИ может быть представлено в виде:

где ${{\theta }^{2}} = \theta _{x}^{2} + \theta _{y}^{2},$ а ${{N}_{{DTR}}}\left( \omega \right)$ − множитель, характеризующий выход ДПИ, зависящий от угла наблюдения и энергии фотонов. Из-за малой интенсивности ПРИ вклад этого механизма излучения не учитывался. Для получения углового распределения излучения от точечного пучка электронов (зависимость 2) распределение 1 свертывалось с двумерным гауссовским распределением с углом расходимости ${{\theta }_{{\text{e}}}} = 15~$ мкрад. Две оставшиеся зависимости соответствуют угловым распределениям для расстояний между кристаллом и детектором 2 и 1 м (кривые (3) и (4)). Для учета возможного влияния статистического разброса измеренных данных зависимости для пучка конечных размеров были “зашумлены”, как и при расчете углового распределения ПРИ на рис. 1.

Как и в случае ПРИ, ошибка в определении параметров подгонки не превышает 5−7%, а “подогнанная” зависимость практически совпадает с зависимостью (4) и поэтому не приводится.

С целью определения чувствительности метода для этого механизма излучения и области энергий электронов был проведен цикл оценок размера пучка, полученных с помощью предлагаемой данной методики, и “зашумленных” угловых распределений от расстояния между кристаллом и детектором. Моделирование выполнено для размеров пучка ${{\sigma }_{x}} = 20~$ мкм и ${{\sigma }_{y}} = 30~$ мкм. Остальные параметры совпадают с описанными выше. Полученная в результате подгонки зависимость оценок размера пучка ${{\tilde {\sigma }}_{{x,y}}}$ от расстояния приведена на рис. 4. Как и для случая ПРИ, выполняется условие R₁= 2R₂, а в качестве ошибок используется стандартное отклонение полученных в результате подгонки значений от среднего.

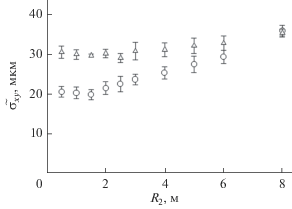
Из рис. 4 видно, что для расстояний между кристаллом и детектором меньше двух метров ошибка оценки размера пучка не превышает 5−7%, а сама оценка совпадаeт со значениями, использованными при моделировании. Для больших расстояний, как и в случае ПРИ, различие между оценкой и размером пучка с увеличением расстояния возрастает. Различие начинает превышать стандартное отклонение для величины R₂, составляющей порядка 2.5 и 5 м для горизонтального и вертикального размеров пучка, соответственно, когда начинает выполняться условие $\sigma _{{x,y}}^{{\text{'}}} = {{{{\sigma }_{{x,y}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{x,y}}}} {{{R}_{2}}}}} \right. \kern-0em} {{{R}_{2}}}} \leqslant $ $ \leqslant 0.1{{\Theta }_{{{\text{ch}}}}},$ где ${{\Theta }_{{{\text{ch}}}}} = {{\gamma }^{{ - 1}}}{\text{.}}$ Как и ранее, для малых значений $\sigma {\text{'}}$ различие распределений для разных расстояний практически отсутствует, и в результате метод теряет чувствительность. Здесь следует отметить, что с возрастанием уровня “шума” различие начинает проявляться для меньших расстояний.

Не менее важным условием является требование ${{\sigma }_{{x,y}}} > {{\delta }_{{x,y}}},$ то есть размер детектора ${{\delta }_{{x,y}}}~$ должен быть сопоставим с характерными размерами пучка частиц на мишени ${{\sigma }_{{x,y}}}.$ Если это условие не выполняется, различие между распределениями для разных расстояний отсутствует. В уже упомянутом эксперименте [8] использовался детектор с размером пикселя 11.2 × 11.6 мкм, поэтому мы можем считать, что минимальный уверенно определяемый размер пучка ~ 10 мкм.

Основным требованием для успешного применения предлагаемого метода измерения размера пучка является равенство телесных углов, перекрываемых элементом детектора для обоих расстояний. Вылет вторичных электронов и квантов из элемента, где произошло взаимодействие фотона с веществом детектора, в соседние искажает измеряемые распределения, сглаживая их. Влияние эффекта сильнее для меньших размеров элемента детектора, поэтому он эквивалентен дополнительному увеличению размера пучка частиц на кристалле.

С целью проверки значимости влияния этого эффекта на результат измерений мы провели моделирование реализации методики с учетом и без учета влияния эффекта вылета вторичных частиц и квантов для следующих условий: энергия электронов 10 ГэВ, кристалл кремния с ориентацией (011), энергия фотонов $\omega = 11.65$ кэВ, размер элемента детектора 10 × 10 мкм и 20 × 20 мкм для расстояния между кристаллом и детектором 1 м и 2 м. Размер пучка электронов на мишени 10 мкм в вертикальной плоскости и 20 мкм в горизонтальной. Расходимость электронного пучка − 10 мкрад. Для упрощения процесса моделирования вместо зависимости (7) использовалось азимутально симметричное спектрально-угловое распределение переходного излучения, часто называемое формулой Гарибяна [21].

Моделирование выполнено методом Монте-Карло для параметров детектора HR25 [22], примененного в эксперименте [8], где использован сцинтиллятор P43 с химическим составом Gd₂SO₂ и толщиной 30 мкм. Методика моделирования параметров детектора приведена в работе [23].

На рис. 5 приведено отношение интенсивностей излучения, зарегистрированное детектором для двух расстояний, в вертикальной (рис. 5а) и горизонтальной (рис. 5б) плоскостях. Моделирование проведено для точечного пучка электронов без учета влияния детектора (кривая); точечного электронного пучка с учетом влияния детектора (треугольники) и протяженного электронного пучка без учета влияния детектора (точки).

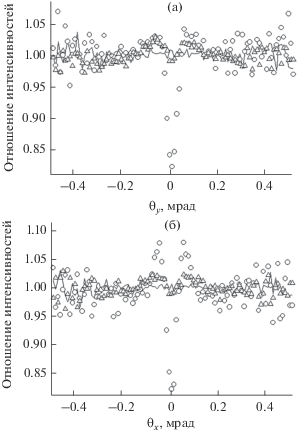
Из рис. 5 следует, что без учета размеров пучка электронов на мишени и влияния вылета вторичных частиц и квантов угловые распределения, измеренные для двух расстояний, совпадают. Разброс значений для больших углов наблюдения обусловлен низкой статистикой из-за резкого уменьшения интенсивности переходного излучения с ростом угла вылета фотонов (рис. 3). Учет процесса вылета вторичных частиц и квантов (треугольники) приводит к определенному отличию угловых распределений на разных расстояниях, но само это отличие достаточно слабо и не превышает нескольких процентов, что близко к статистическому разбросу.

Влияние размера пучка на кристалле (точки) существенно более значимо. Отклонение отношения интенсивностей излучения от единицы достигает 15% и более. Размеры электронного пучка в вертикальной и горизонтальной плоскостях отличаются, поэтому отношение интенсивностей, регистрируемых детектором для двух разных расстояний, в вертикальной и горизонтальной плоскостях то же отличаются, на чем и основан предлагаемый нами метод определения размера пучка электронов в обеих плоскостях. Одновременный учет размеров пучка на мишени и влияния вылета вторичных электронов и квантов практически не изменил соотношение интенсивностей излучения по сравнению с результатами моделирования, где вылет вторичного излучения не учитывался. Поэтому эта зависимость не приводится.

Следовательно, для энергий фотонов около 10 кэВ и размеров пикселя детектора порядка 10 мкм влияние вылета вторичных частиц и квантов в процессе регистрации рентгеновского излучения сравнительно слабо влияет на результаты измерений размеров пучка с помощью предлагаемой методики и (в первом приближении) может не учитываться.

Лазеры на свободных электронах в рентгеновском диапазоне частот [15] работают вплоть до длин волн ~0.1 нм, что соответствует энергии фотонов ~15 кэВ. Таким образом, длина волны, выбранная нами для проверки применимости метода, сопоставима с продольными размерами банча, что недостаточно для исключения когерентных эффектов в излучении. Поперечные размеры пучка электронов в случае реализации ЛСЭ составляют порядка 100 мкм и выше, что позволяет увеличить энергию фотонов за счет уменьшения угла наблюдения, сохраняя достаточно большое расстояние между электронным пучком и осью детектора, которое необходимо для защиты детектора от фона, за счет увеличения расстояния между кристаллом и координатным детектором.

Уменьшение длины волны излучения более чем в 10 раз достижимо, так как в эксперименте [20] для угла наблюдения 4° уверенно регистрировалось ПРИ и ДТИ фотонов с энергией ${\omega }\sim 145~$ кэВ. Увеличение энергии регистрируемых фотонов может привести к усилению влияния вылета вторичных частиц и квантов и требует углубленного анализа, учитывающего энергию регистрируемых фотонов, характеристики выбираемого детектора и другие экспериментальные факторы.

ЗАКЛЮЧЕНИЕ

Поперечные размеры пучка частиц ${{\sigma }_{{x,y}}}$ можно определить по результатам измерения угловых (пространственных) распределений излучения быстрых электронов в тонких кристаллах для двух отличающихся расстояний между источником и координатным детектором. Искомые размеры пучка определяются подгонкой распределения для меньшего расстояния сверткой распределения для большего расстояния с двумерным гауссовским распределением, параметры которого однозначно связаны с размерами пучка и расстояниями между кристаллом и детекторами. Границей применимости метода является условие ${{{{\sigma }_{{x,y}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{x,y}}}} R}} \right. \kern-0em} R} > 0.1{{\Theta }_{{{\text{ch}}}}}.$ Для механизма ПРИ характерный угол ${{\Theta }_{{{\text{ch}}}}}$ совпадает с ${{\Theta }_{{{\text{ph}}}}},$ а для тонких кристаллов и энергий электронов свыше нескольких ГэВ он близок к ${{\gamma }^{{ - 1}}}{\text{.}}$ Для энергии фотонов порядка 10 кэВ и размера элемента координатного детектора 10 × 10 мкм влияние эффекта вылета вторичных электронов и фотонов из пикселя, где произошло взаимодействие рентгеновских фотонов с детектором, в соседние мало и в первом приближении может не учитываться.

Дополнительным требованием является выполнение условия на соотношение характерного размера пучка и размер детектора $\sigma \sim \delta {\text{.}}$ Одновременное выполнение обоих требований ограничивает измеряемый размер пучка величиной 60−100 мкм для механизма ПРИ и энергии электронов менее 1 ГэВ и величиной 10−15 мкм для механизма ДПИ и энергии электронов свыше нескольких ГэВ. Метод может быть использован и для промежуточных энергий электронов, где отсутствует доминирующий тип излучения. Поэтому определить его область чувствительности более сложно. Требуются вычисления, учитывающие вклад всех механизмов излучения, толщину кристалла и другие экспериментальные условия.

В случае необходимости измерений параметров пучков с длиной банча порядка 0.1 нм и менее можно перейти на меньшие углы наблюдения и бóльшую энергию фотонов, что повлечет увеличение эффекта влияния вылета вторичных частиц и квантов из точки, где произошло взаимодействие фотона с веществом детектора, в соседние пиксели. Этот вопрос требует более тщательного исследования, результаты которого будут приведены в следующих работах.

Предлагаемая методика оценки размеров электронного пучка является модельно независимой, не требует точного знания расходимости пучка и степени совершенства структуры кристалла. Главным требованием является идентичность углового распределения излучения в измерениях для разных расстояний между кристаллом и детектором. Методика слабо чувствительна к импульсному нагреву мишени, если он не приводит к разрушению кристалла [24], и может быть использована на интенсивных пучках линейных ускорителей для рентгеновских лазеров на свободных электронах.