Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 10, стр. 84-88
Фазовые переходы в двумерных структурах, описываемых примесными моделями Поттса
А. К. Муртазаев a, А. Б. Бабаев b, c, *, Г. Я. Атаева a, А. А. Муртазаева a
a Институт физики им. Х.И. Амирханова ДФИЦ РАН
367010 Махачкала, Россия
b Дагестанский федеральный исследовательский центр РАН
367000 Махачкала, Россия
c Дагестанский государственный педагогический университет
367003 Махачкала, Россия
* E-mail: akai2005@mail.ru
Поступила в редакцию 12.12.2020
После доработки 22.02.2021
Принята к публикации 25.02.2021
Аннотация
На основе численных методов вычислительной физики исследованы фазовые переходы в двумерной примесной модели Поттса на квадратной решетке. Расчеты проводились для слабо разбавленных систем с периодическими граничными условиями при концентрации спинов p = 0.95. Были рассмотрены системы с линейными размерами L × L = N, L = 10–160. Изучено влияние незначительного беспорядка, реализованного в виде вмороженных немагнитных примесей, на фазовые переходы первого рода. Приведены температурные зависимости теплоемкости, восприимчивости и намагниченности в зависимости от линейных размеров изучаемых систем. С применением метода кумулянтов Биндера четвертого порядка и гистограммного анализа данных показано, что небольшая концентрация примесей с = 5% (с = 1 – p) достаточна для изменения рода фазового перехода – с первого на второй.
ВВЕДЕНИЕ
К настоящему моменту известно, что немагнитные примеси и дефекты структуры влияют на тепловые и магнитные характеристики спиновых систем, если критический индекс теплоемкости, соответствующий “чистой” системе, положителен, т.е. α > 0. В противоположном случае, когда α < 0, слабый беспорядок не влияет на критическое поведение (критерий Харриса [1]). В то же время имеются основания предполагать, что примеси оказывают совершенно другое влияние, вплоть до изменения рода фазового перехода в случае спиновых систем, испытывающих в однородном состоянии фазовый переход первого рода [2].
В работе исследованы фазовые переходы в двумерной слабо разбавленной модели Поттса с числом состояний спина q = 5 на квадратной решетке при концентрации спинов p = 0.95. Исследования проведены на основе кластерного алгоритма Вольфа метода Монте-Карло [3]. Для двумерной модели Поттса с q = 5 до сих пор нет достоверных данных о влиянии незначительной концентрации немагнитных примесей на тепловые и магнитные свойства, не исследовано их влияние на фазовые переходы, нет сведений о зависимости критических индексов от концентрации немагнитных примесей [4]. Единственным надежно установленным фактом является, то, что в “чистой” модели реализуется фазовый переход первого рода согласно аналитическим методам [5].
МОДЕЛЬ И ЧИСЛЕННЫЙ МЕТОД
В узлах i квадратной решетки L × L с периодическими граничными условиями расположены спины ${{S}_{i}}$, которые могут находиться в одном из состояний q = 1, 2, 3, 4, 5, и немагнитные примеси (Si = 0). Немагнитные примеси неподвижны. Энергия связи между двумя узлами равна нулю, если хотя бы в одном узле находится немагнитная примесь или если взаимодействующие спины находятся в различных состояниях, и равна J, если оба узла заняты магнитными атомами, находящимися в одинаковых состояниях. Гамильтониан такой системы можно записать в следующем виде [5]:
(1)
$H = - \frac{1}{2}J\sum\limits_{i,j} {{{\rho }_{i}}{{\rho }_{j}}\delta ({{S}_{i}},{{S}_{j}})} ,\,\,\,\,{{S}_{i}} = 1,2,3,4,5,$и J – параметр обменного ферромагнитного взаимодействия ближайших соседей (в дальнейшем считаем J = 1 и работаем с безразмерной температурой). Концентрация магнитных атомов определяется суммированием всех состояний атомов во всех узлах решетки:
(2)
$p = \frac{{\left( {{{N}_{1}} + ~{{N}_{2}} + {\text{\;}}{{N}_{3}} + ~{{N}_{4}} + {\text{\;}}{{N}_{5}}} \right)}}{{{{L}^{2}}}},$РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
За температурным поведением теплоемкости и восприимчивости наблюдали с использованием флуктуационных соотношений [6]:
(3)
$C = (N{{K}^{2}})\left( {\left\langle {{{U}^{2}}} \right\rangle - {{{\left\langle U \right\rangle }}^{2}}} \right),$(4)
$\chi = (NK)\left( {\left\langle {m_{F}^{2}} \right\rangle - {{{\left\langle {{{m}_{F}}} \right\rangle }}^{2}}} \right),$(5)
${{m}_{F}} = \frac{{\left[ {q\left( {\frac{{{{N}_{{\max }}}}}{N}} \right) - 1} \right]}}{{q - 1}},$На рис. 1 и 2 представлены характерные зависимости восприимчивости χ и теплоемкости C от температуры T для двумерной слабо разбавленной ферромагнитной модели Поттса c числом состояний спина q = 5 на квадратной решетке для систем с линейными размерами L = 10–160 при концентрации спинов p = 0.95. Здесь и далее на всех рисунках погрешность данных не превышает размеров символов, используемых для построения графиков. Отметим, что на зависимостях восприимчивости χ и теплоемкости C от температуры всех исследуемых систем проявляются четко выраженные максимумы, и эти максимумы в пределах погрешности соответствуют одной температуре.
Рис. 1.
Температурная зависимость восприимчивости χ для двумерной примесной модели Поттса с числом состояний спина q = 5 для систем с линейными размерами L = 10–160 при концентрации спинов p = 0.95.
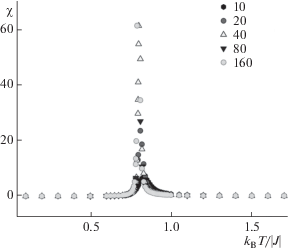
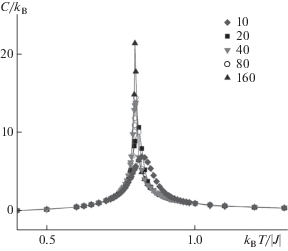
Рис. 2.
Температурная зависимость теплоемкости С для двумерной примесной модели Поттса с числом состояний спина q = 5 для систем с линейными размерами L = 10–160 при концентрации спинов p = 0.95.
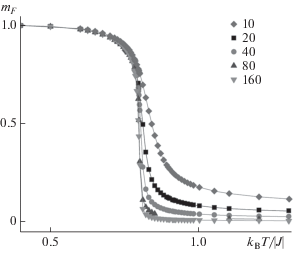
На рис. 3 представлены температурные зависимости намагниченности mF для двумерной трехвершинной слабо разбавленной модели Поттса при p = 0.95. Как видно из рисунка, наблюдается монотонное уменьшение mF c ростом температуры и заметное уменьшение высокотемпературных “хвостов” при увеличении линейного размера L.
Рис. 3.
Температурная зависимость намагниченности mF для двумерной примесной модели Поттса с числом состояний спина q = 5 для систем с линейными размерами L = 10–160 при концентрации спинов p = 0.95.
Для анализа характера фазового перехода применялся метод кумулянтов Биндера четвертого порядка [8]:
(6)
${{V}_{L}}(T,p) = 1 - \frac{{{{{\left\langle {{{E}^{4}}(T,p;L)} \right\rangle }}_{L}}}}{{3\left\langle {{{E}^{2}}(T,p;L)} \right\rangle _{L}^{2}}},$(7)
${{U}_{L}}(T,p) = 1 - \frac{{{{{\left\langle {{{m}^{4}}(T,p;L)} \right\rangle }}_{L}}}}{{3\left\langle {{{m}^{2}}(T,p;L)} \right\rangle _{L}^{2}}},$Рис. 4.
Температурная зависимость кумулянтов Биндера VL(T,p) для примесной модели Поттса для систем с линейными размерами L = 10–160 при концентрации спинов при p = 0.95. На вставке – аппроксимация кумулянтов Биндера VL(T,p) в соответствии с выражением (8).
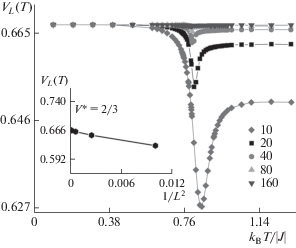
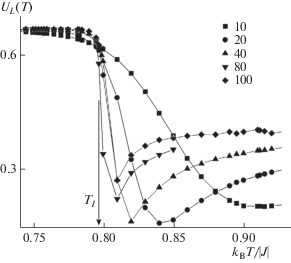
Рис. 5.
Температурная зависимость кумулянтов Биндера UL(T,p) для примесной модели Поттса для систем с линейными размерами L = 10–100 при концентрации спинов p = 0.95. Тl = 0.796.
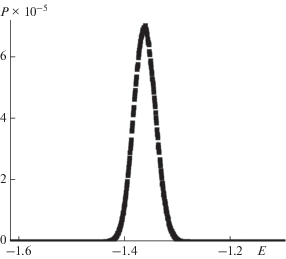
Кроме кумулянтов Биндера для анализа рода фазового перехода был использован и гистограммный анализ данных метода Монте-Карло [12, 13]. Гистограммный анализ, проведенный для двумерной слабо разбавленной ферромагнитной модели Поттса с числом состояний спина q = 5 на квадратной решетке при концентрации спинов p = 0.95, также свидетельствует о фазовом переходе второго рода. На рис. 6 представлена гистограмма распределения энергии вблизи точки фазового перехода Tl для систем с линейным размером L = = 120. Как видно из рисунка, бимодальность гистограммы распределения энергии, наблюдаемую в “чистой” неразбавленной двумерной модели Поттса [14, 15], в случае внесения незначительной концентрации примесей порядка 5% обнаружить не удалось. На зависимости вероятности P от энергии Е системы с L = 120 наблюдается один хорошо выраженный максимум (рис. 6), что является одним из достаточных условий фазового перехода второго рода.
ЗАКЛЮЧЕНИЕ
Таким образом, данные, полученные на основе вычислительного эксперимента, свидетельствуют о том, что в двумерной ферромагнитной модели Поттса с q = 5 внесение небольшого беспорядка в виде немагнитных примесей концентрацией c = 5% (с = 1 – p) каноническим способом достаточно для изменения порядка фазового первого рода – с первого на второй.
Список литературы
Harris A.B. // J. Phys. C. 1974. V. 7. P. 1671.
Aizenman M., Wehr J. // Phys. Rev. Lett. 1989. V. 62. P. 2503.https://doi.org/10.1103/PhysRevLett.62.2503
Wolff U. // Phys. Lett. 1989. V. 62. P. 361.https://doi.org/10.1103/PhysRevLett.62.361
Qian X., Deng Y., Blöte W.J. // Phys. Rev. E. 2005. V. 72. P. 056132.https://doi.org/10.1103/PhysRevE.72.056132
Wu. F.Y. Exactly Solved Models: A Journey in Statistical Mechanics. London: World Scientific, 2009.
Peczac P., Ferrenberg A.M., Landau D.P. // Phys. Rev. B. 1991. V. 43. P. 6087.https://doi.org/10.1103/PhysRevB.43.6087
Chatelain C., Berche B. // Phys. Rev. Lett. 1998. V. 80. P. 1670.https://doi.org/10.1103/PhysRevLett.80.1670
Eichhorn K., Binder K. // J. Phys.: Condens. Matter. 1996. V. 8. P. 5209.https://doi.org/10.1088/0953-8984/8/28/005
Murtazaev A.K., Babaev A.B. // J. Surf. Invest.: X-ray, Synchrotron Neutron Tech. 2020. V. 14. P. 727.https://doi.org/10.1134/S1027451020030350
Murtazaev A.K., Babaev A.B. // Phys. Solid State. 2020. V. 62. № 5. P. 851.https://doi.org/10.1134/S1063783420050042
Murtazaev A.K., Babaev A.B. // Mater. Lett. 2020. V. 258. P. 126771.https://doi.org/10.1016/j.matlet.2019.126771
Alves N.A., Berg B.A., Villanova R. // Phys. Rev. B. 1990. V. 41. P. 383.https://doi.org/10.1103/PhysRevB.41.383
Wang F., Landau D.P. // Phys. Rev. E. 2001. V. 64. P. 056101.https://doi.org/10.1103/PhysRevE.64.056101
Babaev A.B., Murtazaev A.K. // Low Temp. Phys. 2020. V. 46. P. 688.https://doi.org/10.1063/10.0001365
Murtazaev A.K., Babaev A.B., Ataeva G.Ya. // Phys. Solid State. 2020. V. 62. № 7. P. 1228.https://doi.org/10.1134/S1063783420070185
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования