Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 11, стр. 23-27

ВВЕДЕНИЕ

В двумерных электронных системах спектр магнитоплазменных волн формируют бернштейновские моды [1, 2] с частотами в диапазоне между гармониками циклотронного резонанса и щелями вблизи этих гармоник. Первоначально предсказанные [1] для классической плазмы в отсутствие рассеяния электронов бернштейновские моды наблюдались в самых разных системах, включая установки термоядерного синтеза [3], а также регистрировались в спектрах космического излучения [4]. В двумерных электронных системах фрагменты закона дисперсии этих мод формируют широко известный спектр магнитоплазмонов:

Здесь ω_c = eB/m*c – циклотронная частота электронов с эффективной массой m* в магнитном поле с индукцией B, перпендикулярном двумерной электронной системе, V_F – фермиевская скорость электронов в вырожденной двумерной электронной системе, k – волновой вектор магнитоплазмона, ε_eff(k) – эффективная диэлектрическая проницаемость среды вокруг двумерной электронной системы, в которую проникает электрическое поле магнитоплазмона. Резонансному поглощению электромагнитного излучения магнитоплазмонами в двумерной электронной системе посвящено множество исследований (например, [5]). Выражение (1), однако, справедливо только в ограниченном диапазоне волновых векторов и на удалении от гармоник циклотронного резонанса. Наиболее убедительной идентификацией бернштейновских мод является их наблюдение вне области применимости этого выражения. Такие наблюдения [6, 7] были осуществлены при достаточно больших абсолютных значениях волнового вектора, для чего на поверхность полупроводника наносили периодическую систему металлических полосок с малым периодом, определяющую волновой вектор возбуждаемой излучением магнитоплазменной волны [8]. Недостатком этой методики является плохо определенная зависимость ε_eff(k) для таких систем. Эксперименты [6, 7] были выполнены в дальней инфракрасной области спектра и соответствующих ей довольно сильных магнитых полях $B \gtrsim 1~\,\,{\text{Tл}}$, что определило область значений параметра $k{{R}_{{\text{c}}}} \lesssim 1$, где R_c = V_F/ω_c – циклотронный радиус электрона на уровне Ферми. Более интересная область, соответствующая $k{{R}_{{\text{c}}}} \gg 1$, была достигнута в [9] при исследованиях резонансного микроволнового поглощения, индуцированного пропусканием поверхностной акустической волны, определяющей абсолютное значение волнового вектора. Свойства диэлектрического окружения были хорошо определены и не изменялись при пропускании поверхностной акустической волны. Однако эти результаты количественно с теорией не сравнивали. Для полноты картины отметим недавнее наблюдение размерных резонансов бернштейновских мод, соответствующих малым абсолютным значениям волнового вектора, определяемым латеральным размером образца [10].

В настоящей работе выполнено сравнение рассчитанного закона дисперсии бернштейновских мод с результатами измерений [9]. Особое внимание уделено области $k{{R}_{{\text{c}}}} \gg 1$, где закон дисперсии бернштейновских мод демонстрирует универсальные особенности. Кроме того, построены диаграммы интенсивности поглощения в зависимости от частоты и волнового вектора электромагнитного излучения, лежащего в плоскости двумерной электронной системы. Эти результаты демонстрируют резонансное поглощение излучения бернштейновскими модами, особенно сильное в областях волновых векторов и частот, близких к спектру магнитоплазмонов (1).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Рассмотрим сначала соотношение между спектром магнитоплазмонов (1) и законом дисперсии ω(k) бернштейновских мод в квазистатическом пределе (ω < ck/ε_eff), являющимся решением уравнения [11–13]:

Здесь J_n – функция Бесселя порядка n. Отметим, прежде всего, что уравнение (1) может быть получено из уравнения (2) при $k{{R}_{{\text{c}}}} \ll 1$ вдали от гармоник циклотронного резонанса. Действительно, тогда при разложении функций Бесселя по малому параметру kR_c основным будет член, возникающий из разложения первого слагаемого суммы и пропорциональный (kR_c)². Легко проверить, что решение уравнения (2) с учетом только такого члена разложения приводит к выражению (1). Нетрудно видеть, что функция ω(k), возникающая в результате решения уравнения (2), не может пересекать уровни ω = nω_c, так как знаменатель соответствующего члена в сумме обращается в ноль, однако может приближаться к ним сверху при значениях $k{{R}_{{\text{c}}}} = {{j}_{{n,s}}}$, где ${{j}_{{n,s~}}}$ – нули функции Бесселя J_n с порядковым номером s = 1, 2, … Значит, решения ω(k) уравнения (2) должны составить набор дисперсионных зависимостей, лежащих в интервалах частот (nħω_c, (n + 1)ħω_c).

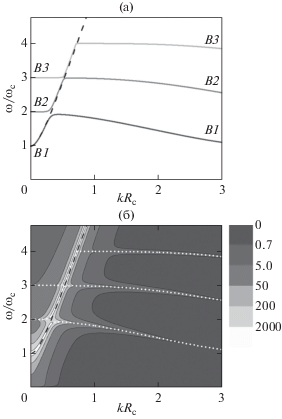
Дальнейшее сравнение бернштейновских мод и магнитоплазмона выполним для случая двумерной электронной системы в полевом транзисторе, т.е. для системы, находящейся внутри массивного полупроводника с диэлектрической проницаемостью χ на расстоянии d от его поверхности, на которую нанесен металлический слой (затвор). В этом случае ${{{{\varepsilon }}}_{{{\text{eff}}}}}\left( k \right) = \,\,~{{\chi }}{{\left( {1~\,\, + \,\,~{\text{cth}}\left( {kd} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {1~\,\, + \,\,~{\text{cth}}\left( {kd} \right)} \right)} 2}} \right. \kern-0em} 2}$ [14]. При $kd~\,\, \ll 1~$ ${{{{\varepsilon }}}_{{{\text{eff}}}}}\left( k \right) = {{~{{\chi }}} \mathord{\left/ {\vphantom {{~{{\chi }}} {2kd}}} \right. \kern-0em} {2kd}}$, и множитель перед суммой перестает зависеть от волнового вектора. Очевидно, что в этом случае уравнение (2) определяет соотношение между ω/ω_c и kR_c, которое не зависит от абсолютных значений волнового вектора и магнитного поля по отдельности, т.е. закон дисперсии параметризуется в координатах (kR_c, ω/ω_c). На рис. 1а представлены результаты расчета по формуле (2) закона дисперсии трех нижних по частоте бернштейновских мод и спектра магнитоплазмонов (1) для значений параметра kR_c < 3. Каждая из ветвей закона дисперсии лежит в одном из интервалов частот ($\ell $ω_c, ($\ell $ + 1)ω_c) с $\ell $ = 1, 2, 3 и может быть пронумерована числом $\ell $ (индексы около обозначений В бернштейновских мод на рис. 1а). Бернштейновские моды имеют щели по частоте на гармониках циклотронного резонанса, наибольшая из которых возникает около второй гармоники ω/ω_c = 2. Спектр магнитоплазмонов, показанный штриховой кривой, таких щелей не описывает и перекрывается с небольшими участками законов дисперсии различных мод при $\ell $ω_c < ω < < ($\ell $ + 1)ω_c и kR_c < 1. Вне этих участков остается заметная часть закона дисперсии бернштейновских мод.

Для дальнейшего сравнения представляет интерес оценка силы осциллятора для магнитоплазменных волн соответствующей области закона дисперсии. Эта оценка может быть сделана на основе квазиклассической формулы [15] для поглощения высокочастотного электрического поля вида E_ω = = Eexp(i(kr – ωt)) с зависимостью от координаты r в плоскости двумерной электронной системы, соответствующей полю магнитоплазменной волны:

Отметим, что в формуле (3) учтено рассеяние электронов за счет введения времени их импульсной релаксации τ. Результаты расчета интенсивности поглощения представлены на рис. 1б для той же области на плоскости (kR_c, ω/ω_c), что и законы дисперсии на рис. 1а. Эти результаты, однако, теперь не полностью параметризуются в выбранных координатах. Такая параметризация имеет место только при ω_cτ → ∞. При выбранных для расчета значениях τ = 80 × 10^–12 с и B = 0.1 Тл ω_cτ ≈ 20, и требуемое соотношение неплохо выполняется. Отметим, что вычисленные максимумы поглощения совпадают с линиями дисперсии бернштейновских мод (2). Более того, уравнение (2) можно получить из (3), приравняв к нулю производную ${{\partial Q} \mathord{\left/ {\vphantom {{\partial Q} {\partial {{\omega }}}}} \right. \kern-0em} {\partial {{\omega }}}}$, а затем перейдя к пределу ωτ → ∞. Важным результатом расчета на рис. 1б является сильное поглощение около областей перекрытия бернштейновских мод с магнитоплазмоном. Этот факт определяет доминирование этих областей в поглощении и более простое экспериментальное наблюдение спектра магнитоплазмона по сравнению с другими участками дисперсии бернштейновских мод. Необходимо, однако, отметить существование локальных минимумов поглощения на линии, соответствующей спектру (1), возникающих около гармоник циклотронного резонанса. Такой минимум хорошо различим на рис. 1б около второй гармоники (ω/ω_c = 2). Все отмеченные особенности (локальные максимумы поглощения на бернштейновских модах, частичное перекрытие спектра магнитоплазмонов с дисперсией бернштейновских мод, а также максимальное поглощение в областях перекрытия) сохраняются и в случае двумерной электронной системы без затвора, хотя в этом случае параметризация законов дисперсии в координатах (kR_c, ω/ω_c) выполняется только приближенно и при достаточно больших значениях kR_c, как это будет видно ниже.

Перейдем к анализу результатов для двумерной электронной системы без затвора. В образцах гетероструктур с двумерной электронной системой, находящейся вблизи поверхности, достаточно хорошим приближением для эффективной диэлектрической проницаемости является выражение ε_eff(k) = (χ + 1)/2, где χ – диэлектрическая проницаемость материала гетероструктуры. Будем рассматривать гетероструктуру на основе GaAs, для которой χ = 12.8. Расчеты выполнены для абсолютных значений волновых векторов, реализованных в [9]. В этой работе были обнаружены и исследованы пики микроволнового магнитопоглощения, возникающие при генерации поверхностной акустической волны в образцах гетероструктур GaAs/AlGaAs с двумерной электронной системой без затвора. Очевидно, что возникновение таких пиков связано с возбуждением магнитоплазменной волны с волновым вектором, равным волновому вектору поверхностной акустической волны. Длина этого вектора определялась периодом встречно-штыревого преобразователя, использовавшегося для генерации поверхностной акустической волны. Исследования были выполнены на серии из пяти образцов, изготовленных из одной и той же гетероструктуры, но имеющих различные периоды преобразователя, соответствующие волновым векторам (5.25–197) × 10⁵ м^–1. Поверхностные акустические волны возбуждали на частоте, соответствующей их резонансу в конкретном преобразователе. Диапазон частот возбуждения составил от 0.24 до 9 ГГц. Микроволновое поглощение измеряли на более высоких частотах – от 20 до 180 ГГц. Основная часть данных получена в магнитных полях с индукцией 0.1–0.3 Тл. Преобразователь изготавливали на части поверхности образца вне области, в которой проводили измерения поглощения методом фотолюминесценции. Плотность электронов во всех образцах n_s = 3.9 × 10¹⁴ м^–2. Более подробная информация о деталях эксперимента дана в [9]. Возбуждение поверхностных акустических волн приводило к модуляции свойств двумерной электронной системы, а также к возникновению периодического электрического поля в силу пьезоэлектрических свойств материала гетероструктуры. Появление периодического возмущения в двумерной электронной системе обеспечивает связь между падающей электромагнитной волной и магнитоплазменной волной с соответствующим волновым вектором, аналогично тому, как это было установлено в структурах с затвором, образованным периодической системой металлических полосок [8]. Индуцированные поверхностными акустическими волнами пики микроволнового поглощения ожидаются на линиях дисперсии магнитоплазменных волн, т.е. бернштейновских мод.

Результаты расчетов закона дисперсии, полученные в ходе решения уравнения (2) для различных фиксированных абсолютных значений волнового вектора, использованных в [9], и изменяющегося магнитного поля, показаны на рис. 2 сплошными линиями. Отметим почти полное совпадение рассчитанных кривых при kR_c > 1, т.е. их приближенную параметризацию в этой области. Анализ уравнения (2) показывает, что эта параметризация обусловлена большим фактором перед суммой для всех рассмотренных значений k. Действительно, минимальная величина этого фактора, получаемая при самом большом волновом векторе, равна 37. В таком случае в уравнении (2) можно пренебречь единицей. Закон же дисперсии, полученный в результате решения такого упрощенного уравнения, очевидно, параметризуется в координатах (kR_c, ω/ω_c). Такое решение для нижней бернштейновской моды показано на рис. 2 крестиками. Оно действительно хорошо совпадает с решениями полного уравнения (2).

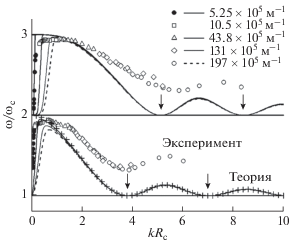
Еще одной особенностью решений уравнения (2) является универсальное положение минимумов на каждой ветви бернштейновских мод. Для моды с номером 𝓁 эти минимумы находятся в точках $\left( {{\text{\;}}{{j}_{{\ell ,~s{\text{\;}}}}},\ell } \right)$, где значения ${{j}_{{\ell ,~s{\text{\;}}}}}$ являются нулями функции Бесселя порядка 𝓁, и s = 1, 2, … . Очевидно, эти универсальные значения – результат нелокальной связи между высокочастотными полем и током и отражают эффект соизмеримости волнового вектора плазменного возбуждения с циклотронным радиусом электронов на поверхности Ферми [15]. Сравним результаты расчета и эксперимента. Отметим, что в расчете фактически отсутствуют подгоночные параметры. Экспериментальные данные подтверждают параметризацию закона дисперсии бернштейновских мод в координатах (kR_c, ω/ω_c) при kR_c > 1, где точки, полученные при разных абсолютных значениях волнового вектора, совпадают. В этой области экспериментальные и теоретические кривые демонстрируют немонотонную зависимость от kR_c, причем в случае нижней моды все они имеют минимум, находящийся вблизи kR_c ≈ 3.8, где обращается в ноль функция J₁(kR_c). Однако экспериментальное значение величины ω/ω_c в этом минимуме заметно отличается от вычисленного, что может быть связано с необходимостью более тщательного учета факторов реального эксперимента. Для второй моды также наблюдается немонотонная зависимость с минимумом, однако здесь различаются и положение, и глубина минимума. Таким образом, расчет и эксперимент демонстрируют хорошее качественное согласие.

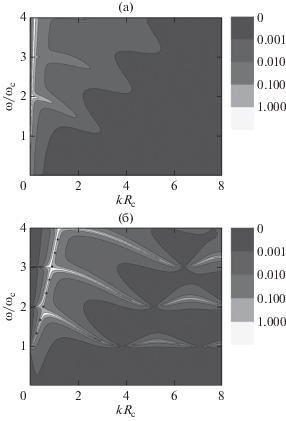
На рис. 3 приведены результаты расчета поглощаемой микроволновой мощности для минимального и максимального экспериментальных абсолютных значений волнового вектора. Так же, как и на рис. 1б, положения максимумов поглощения совпадают с линиями дисперсии соответствующих бернштейновских мод, представленных на рис. 2. Из сравнения рис. 3а и 3б нетрудно видеть, что возможность наблюдения поглощения бернштейновскими модами, включая все его особенности, в области kR_c > 1 сильно возрастает при увеличении длины волнового вектора. Этот результат также коррелирует с наблюдениями [9].

ЗАКЛЮЧЕНИЕ

Выполнен анализ законов дисперсии бернштейновских мод и силы их осциллятора. Установлены основные характерные особенности этой дисперсии, которые качественно подтверждаются экспериментальными результатами.