Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 4, стр. 90-97
Модель роста эпитаксиальных пленок сплава Гейслера
И. В. Воротынцев a, А. Э. Рассадин b, *, Л. А. Фомин b, c, **, И. В. Маликов c
a Нижегородский государственный технический университет
603950 Нижний Новгород, Россия
b Нижегородское математическое общество
603950 Нижний Новгород, Россия
c Институт проблем технологии микроэлектроники и особочистых материалов РАН
142432 Черноголовка, Московская область, Россия
* E-mail: brat_ras@list.ru
** E-mail: fomin@iptm.ru
Поступила в редакцию 10.06.2020
После доработки 17.08.2020
Принята к публикации 22.08.2020
Аннотация
Проведено сравнение экспериментально изученной морфологии поверхности пленок сплава Гейслера Fe2CoAl с теорией формирования фрактальной поверхности пленок. В основу этой теории положена задача Коши для упрощенного уравнения Кардара–Паризи–Жанга. Показано, что для начального фрактального профиля пленки ее можно сразу решить, применяя принцип Олейник–Лакса (слабое решение задачи). В рамках метода простого перебора предложена численная реализация принципа Олейник–Лакса. Введен векторный критерий качества роста поверхности исследуемой пленки. В качестве компонентов этого критерия апробированы следующие функционалы: норма спектральной плотности автокорреляционной функции поверхности пленки в гильбертовом пространстве, информация по Шеннону и фрактальная размерность поверхности пленки. Все эти функционалы вычисляются по профилю поверхности пленки в каждый момент времени. Описана методика получения образцов сплава Гейслера Fe2CoAl.
ВВЕДЕНИЕ
В последнее десятилетие во всем мире различные варианты сплавов Гейслера подвергаются интенсивным исследованиям. Значительный интерес к этим тройным соединениям переходных металлов с элементами III–V групп обусловлен перспективностью их применения в спинтронике. В зонной структуре некоторых из этих соединений уровень ферми находится в запрещенной зоне для электронов со спинами вверх (или вниз), в то время как для электронов с противоположными спинами это не так. Таким образом, ток переносят исключительно электроны с одним направлением спинов. Благодаря этому в спиновых вентилях на основе сплавов Гейслера было достигнуто гигантское магнитосопротивление: 40% при комнатной температуре и 200% при 10 К [1]. Однако помимо зонной структуры важную роль в увеличении магнитосопротивления играет морфология границы раздела. Следовательно, для понимания механизма максимизации магнитосопротивления необходим анализ моделей пространственно-временнóй эволюции поверхности пленок при их росте.
К настоящему времени предпринято довольно много попыток описания формирования неоднородного рельефа на поверхности твердого тела в разных физических ситуациях с помощью дифференциальных уравнений в частных производных следующего вида [2–4]:
(1)
$\frac{{\partial H}}{{\partial t}} = F\left( {\frac{{\partial H}}{{\partial {{x}_{1}}}},\frac{{\partial H}}{{\partial {{x}_{2}}}},\frac{{{{\partial }^{2}}H}}{{\partial x_{1}^{2}}},\frac{{{{\partial }^{2}}H}}{{\partial {{x}_{1}}\partial {{x}_{2}}}},\frac{{{{\partial }^{2}}H}}{{\partial x_{2}^{2}}}, \ldots } \right),$Как правило [2–4], для уравнения (1) ставится задача Коши, начальное условие
(2)
$H({\mathbf{x}},0) = {{H}_{0}}({\mathbf{x}}),\,\,\,\,{\mathbf{x}} \in {{\Omega }_{0}} \subset {{R}^{2}}$В настоящей работе эта процедура применена к описанию роста поверхности пленок сплава Гейслера Fe2CoAl. Приведена методика экспериментов, в результате которых получены образцы сплавов Гейслера. Предложена математическая модель роста этих образцов. Описаны результаты численных расчетов временнóй эволюции толщины пленки сплава Гейслера и ряда функционалов, связанных с этой физической величиной.
МЕТОДИКА ЭКСПЕРИМЕНТА
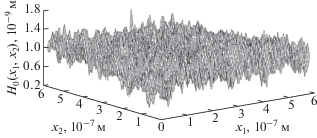
Эпитаксиальные пленки сплава Гейслера Fe2CoAl выращивали методом импульсного лазерного испарения в сверхвысоком вакууме на R-плоскости сапфира (Al2O3) c подслоем вольфрама (W) толщиной 10 нм c ориентацией (001) и без подслоя при температурах подложки 20–550°С. Скорость роста пленок $с$ составляла 4 нм/мин, для получения средней толщины пленки 80 нм было выбрано время роста $\tau $ 20 мин. Технология выращивания пленок сплава Гейслера была аналогична той, которую с успехом применяли для эпитаксиального выращивания пленок никеля и железа на сапфире [5, 6]. Для исследований их морфологии использовали атомно-силовой микроскоп P47 solver НТ-МДТ, с помощью которого определяли начальный рельеф ${{H}_{0}}({\mathbf{x}})$ поверхности подложки (2) и пленки $\tilde {H}({\mathbf{x}},{\tau })$ после окончания ее роста в момент времени $\tau $. Исследовали участки поверхности размерами 0.5 × 0.5 мкм с разрешением 512 × 512 точек. Измерения проводили в полуконтактном режиме с использованием кантилеверов Tipsnano с резонансной частотой около 180 кГц.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РОСТА ПЛЕНОК
Гипотезу о виде правой части уравнения (1), описывающего рост поверхности пленок сплава Гейслера Fe2CoAl, сформулируем, отталкиваясь от феноменологической модели Кардара–Паризи–Жанга (КПЖ) [4]:
где $\nabla $ – двумерный градиент.Это уравнение описывает два конкурирующих процесса: рост поверхности строго по локальной нормали ${\mathbf{n}}({\mathbf{x}},t) = \left( {\begin{array}{*{20}{c}} {\frac{{ - \nabla H}}{{\sqrt {1 + {{{(\nabla H)}}^{2}}} }},}&{\frac{1}{{\sqrt {1 + {{{(\nabla H)}}^{2}}} }}} \end{array}} \right)$ к ней со скоростью $с$ и поверхностную диффузию осаждающегося на этой поверхности вещества с коэффициентом поверхностной диффузии ν.
Однако уравнение (3) нелинейно и потому чрезвычайно сложно для исследования. Упростим его, рассмотрев малоугловое приближение: $\left| {\nabla H} \right| \ll 1.$ Тогда после разложения, входящего в правую часть этого уравнения квадратного корня в ряд Тейлора получим:
Для уравнения (4) известны точные решения [7], однако будем считать, что характерная высота поверхности $H$ удовлетворяет неравенству $H \gg {\nu \mathord{\left/ {\vphantom {\nu c}} \right. \kern-0em} c}.$ В этом случае второй член в правой части уравнения (4) доминирует над третьим членом. Это означает, что поверхностной диффузией можно пренебречь.
Таким образом, будем предполагать, что рост поверхности пленок сплава Гейслера Fe2CoAl описывается следующей упрощенной моделью КПЖ:
Решение $H({\mathbf{x}},t)$ уравнения (5) с начальным условием (2) в момент времени $t$ с помощью метода характеристик [8] записывается неявно:(6)
${\mathbf{x}} = {\mathbf{y}} - ct\nabla {{H}_{0}}({\mathbf{y}}),\,\,\,\,{\mathbf{y}} \in {{\Omega }_{0}},$(8)
${\rm H}({\mathbf{y}},t) = ct + {{H}_{0}}({\mathbf{y}}) - \frac{{ct}}{2}{{(\nabla {{H}_{0}}({\mathbf{y}}))}^{2}},$Однако представление решения уравнения КПЖ (5) в виде выражений (6)–(8) справедливо только до некоторого момента времени ${{t}_{*}}$ – до наступления так называемой градиентной катастрофы [8]. После же градиентной катастрофы решение уравнения (5) строится с помощью принципа абсолютного максимума Олейник–Лакса [8].
Для того чтобы определить величину ${{t}_{*}},$ нужно обратиться к геометрическому смыслу переменных х и у, входящих в формулы (6)–(8). Вектор ${\mathbf{y}} \in {{\Omega }_{0}}$ является вектором лагранжевых координат, которые по формуле (6) преобразуются в эйлеровы координаты х. Для получения высоты пленки $H({\mathbf{x}},t)$ необходимо обратить (6), т.е. получить зависимость лагранжевых координат от эйлеровых ${\mathbf{y}} = {\mathbf{y}}({\mathbf{x}},t)$ в момент времени $t$ и подставить эту зависимость в формулу (7).
Взаимная однозначность отображения (6) определяется его якобианом:
(9)
$J({\mathbf{y}},t) = \det \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {{x}_{1}}({\mathbf{y}},t)}}{{\partial {{y}_{1}}}}}&{\frac{{\partial {{x}_{1}}({\mathbf{y}},t)}}{{\partial {{y}_{2}}}}} \\ {\frac{{\partial {{x}_{2}}({\mathbf{y}},t)}}{{\partial {{y}_{1}}}}}&{\frac{{\partial {{x}_{2}}({\mathbf{y}},t)}}{{\partial {{y}_{2}}}}} \end{array}} \right].$Вычисление величины (9) с помощью формулы (6) дает:
(10)
$J({\mathbf{y}},t) = 1 - cyty{{\nabla }^{2}}{{H}_{0}}({\mathbf{y}}) + {{c}^{2}}y{{t}^{2}}yHe({\mathbf{y}}),$(11)
$He({\mathbf{y}}) = \det \left[ {\begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}{{H}_{0}}({\mathbf{y}})}}{{\partial y_{1}^{2}}}}&{\frac{{{{\partial }^{2}}{{H}_{0}}({\mathbf{y}})}}{{\partial {{y}_{1}}\partial {{y}_{2}}}}} \\ {\frac{{{{\partial }^{2}}{{H}_{0}}({\mathbf{y}})}}{{\partial {{y}_{2}}\partial {{y}_{1}}}}}&{\frac{{{{\partial }^{2}}{{H}_{0}}({\mathbf{y}})}}{{\partial y_{2}^{2}}}} \end{array}} \right].$Время ${{t}_{*}},$ когда отображение (6) теряет свою взаимную однозначность, и место ${{{\mathbf{y}}}_{*}},$ где это происходит, т.е. пространственно-временнóе положение градиентной катастрофы, находятся из системы уравнений:
На рис. 1 приведен типичный результат измерения начального рельефа поверхности исследуемых образцов с помощью атомно-силового микроскопа (АСМ). Из этого рисунка видно, что функция ${{H}_{0}}({\mathbf{x}})$ является существенно негладкой и, вообще говоря, фрактальной во всей области своего определения. Очевидно также, что любые попытки какой-либо аппроксимации [9] этих экспериментальных данных с гладкостью не меньше третьего порядка для того чтобы задать функцию (10), входящую в уравнения (12), обречены на неудачу. К счастью, вычислительный эксперимент, проведенный в [10] для одномерного варианта уравнения (5), т.е. для поверхностей с цилиндрической образующей, показал, что для начального профиля со сколько-нибудь заметной фрактальностью градиентная катастрофа наступает практически мгновенно. Это означает, что можно сразу применять принцип абсолютного максимума Олейник–Лакса, дающий слабое решение задачи Коши для уравнения (5).Напомним, следуя [8], основные положения этого принципа. Выделим из функции $H({\mathbf{x}},t)$ однородный рост высоты пленки:
где $h({\mathbf{x}},t)$ – приведенная высота поверхности, и рассмотрим следующую функцию пяти переменных:(14)
$G({\mathbf{y}};{\mathbf{x}},t) = {{H}_{0}}({\mathbf{y}}) - \frac{{{{{({\mathbf{y}} - {\mathbf{x}})}}^{2}}}}{{2сt}},$Пусть ${{{\mathbf{y}}}_{w}}({\mathbf{x}},t)$ – точка абсолютного максимума функции (14) при фиксированных х и t, которая найдена каким-либо методом:
(15)
${{{\mathbf{y}}}_{w}}({\mathbf{x}},t) = \arg \mathop {\max }\limits_{{\mathbf{y}} \in {{\Omega }_{0}}} G({\mathbf{y}};{\mathbf{x}},t).$Тогда согласно принципу Олейник–Лакса приведенная высота поверхности равна:
ЧИСЛЕННЫЕ РАСЧЕТЫ В РАМКАХ ПРЕДЛОЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Для соответствия с методикой проведенного эксперимента в качестве области ${{\Omega }_{0}}$ целесообразно выбрать квадрат ${{\Omega }_{0}} = (0,L) \times (0,L)$ со стороной L = 0.5 мкм. Поскольку данные АСМ о высоте поверхности образцов представляют собой квадратную матрицу большого размера, естественно в области ${{\Omega }_{0}}$ ввести квадратную сетку ${{\omega }_{\Delta }} = \left\{ {(l\Delta ,m\Delta )} \right.;$ $l,m = \overline {1,N} \} $ с $N = 512$ и шагом $\Delta = {L \mathord{\left/ {\vphantom {L {N \approx 1}}} \right. \kern-0em} {N \approx 1}}$ нм. Результаты измерений начального профиля ${{H}_{0}}({\mathbf{x}})$ в момент времени $t = 0$ и приведенной высоты образца $h({\mathbf{x}},t)$ в моменты времени $t = {{t}_{k}}$ становятся сеточными функциями на ${{\omega }_{\Delta }}{\text{:}}$ $h_{{lm}}^{0} = {{H}_{0}}(l\Delta ,m\Delta )$ и $h_{{lm}}^{k} = h(l\Delta ,m\Delta ,{{t}_{k}})$ соответственно.
Максимум (15) функции (14) принципа Олейник–Лакса отыскивали методом простого перебора, а именно для фиксированного вектора ${\mathbf{x}} \in {{\omega }_{\Delta }}$ при $t = {{t}_{k}}$ вычисляли значения функции (14), когда вектор y пробегал всю сетку ${{\omega }_{{\Delta }}}.$ Затем по найденным индексам $(l,m),$ соответствующим максимальной величине этой функции, определялся вектор ${\mathbf{y}}_{{lm}}^{k},$ т.е. отображение эйлеровых координат в лагранжевы в момент времени ${{t}_{k}}$ на сетке ${{\omega }_{{\Delta }}},$ и затем по нему рассчитывали по формуле (16) приведенную высоту поверхности $h({\mathbf{x}},t)$. Результаты этих расчетов приведены на рис. 2.
Рис. 2.
Результат моделирования поверхности растущей пленки согласно теории КПЖ при нормированном времени роста t/t0: 1 × 10–6 (a); 5 × 10–5 (б); 1 × 10–4 (в); 5 × 10–4 (г); 1 × 10–3 (д); 5 × 10–3 (е); 1 × 10–2 (ж); 5 × 10–2 (з); 1 × 10–1 (и).

Знание сеточной функции $h_{{lm}}^{k}$ позволяет исследовать временну́ю эволюцию таких важных характеристик приведенной высоты h(x, t) поверхности образца, как автокорреляционная функция
(17)
$K({\mathbf{x}},t) = \left\langle {h({\mathbf{\xi }},t)h({\mathbf{\xi }} + {\mathbf{x}},t)} \right\rangle $(18)
$S({\mathbf{q}},t) = \frac{1}{{2\pi }}\int\limits_{{{\Omega }_{0}}} {K({\mathbf{x}},t)\exp ( - i{\mathbf{q}} \cdot {\mathbf{x}}){{d}^{2}}x} .$(19)
${{\left\| S \right\|}_{2}}(t) = {{\left[ {\int\limits_{{{R}^{2}}} {{{{\left| {S({\mathbf{q}},t)} \right|}}^{2}}} {{d}^{2}}q} \right]}^{{\frac{1}{2}}}},$Для того чтобы избежать вычисления двумерного преобразования Фурье в (18) и последующего интегрирования по всей плоскости, величину (19) удобно переписать с помощью формулы Планшереля следующим образом:
(20)
${{\left\| S \right\|}_{2}}(t) = {{\left[ {\int\limits_{{{\Omega }_{0}}} {{{K}^{2}}({\mathbf{x}},t)} {{d}^{2}}x} \right]}^{{\frac{1}{2}}}}.$Для приведенной высоты поверхности $h({\mathbf{x}},t)$ можно рассмотреть еще один функционал – информацию по Шеннону:
(21)
$I[h({\mathbf{x}},t)] = - \frac{1}{{\sigma _{0}^{2}}}\int\limits_{{{\Omega }_{0}}} {\frac{{\left| {h({\mathbf{x}},t)} \right|}}{{{{\sigma }_{0}}}}{{{\log }}_{2}}} \frac{{\left| {h({\mathbf{x}},t)} \right|}}{{{{\sigma }_{0}}}}{{d}^{2}}x,$По известной сеточной функции $h_{{lm}}^{k}$ функционалы (20) и (21) можно оценить следующим образом:
(22)
${{I}_{k}} \approx - \frac{{{{\Delta }^{2}}}}{{\sigma _{0}^{2}}}\sum\limits_{l = 1}^N {\sum\limits_{m = 1}^N {\frac{{\left| {h_{{lm}}^{k}} \right|}}{{{{\sigma }_{0}}}}} } {{\log }_{2}}\frac{{\left| {h_{{lm}}^{k}} \right|}}{{{{\sigma }_{0}}}}$(23)
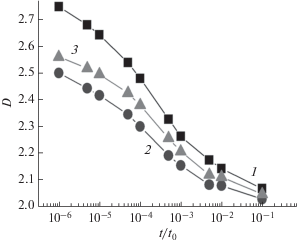
${{\left\| S \right\|}_{2}}({{t}_{k}}) \approx \Delta {{\left[ {\sum\limits_{l = 1}^N {\sum\limits_{m = 1}^N {{{{(K_{{lm}}^{k})}}^{2}}} } } \right]}^{{\frac{1}{2}}}},$Приведенная высота поверхности $h({\mathbf{x}},t)$ в каждый момент времени также может быть охарактеризована своей фрактальной размерностью. На рис. 5 показана зависимость фрактальной размерности смоделированного согласно теории КПЖ рельефа поверхности пленок, растущих на подложке сапфира, от нормированного времени роста. Эту величину оценивали с помощью методик [11] подсчета кубов, триангуляции, декомпозиции.
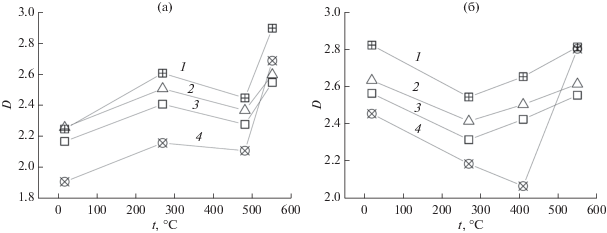
На рис. 6 показаны зависимости фрактальной размерности пленок сплава Гейслера от температуры роста, вычисленные по АСМ-изображениям с помощью разных методик [11]: подсчета кубов, триангуляции, декомпозиции, а также расчета спектральной плотности флуктуаций. Для пленок, выращенных с подслоем W, фрактальная размерность повышается с увеличением температуры роста, однако имеется локальный минимум при 480°C. Фрактальная размерность пленок, выращенных без подслоя, минимальна при 270°C, однако метод спектральной плотности показывает минимум при большей температуре. Возможно, это связано с ошибками, вносимыми прибором при сканировании поверхности. Таким образом, оптимальная по фрактальной размерности температура роста пленок без подслоя составляет 270°C, а с подслоем W 480°C.
Рис. 3.
Зависимость количества информации смоделированной поверхности растущей пленки согласно теории КПЖ от нормированного на размер скана времени роста.
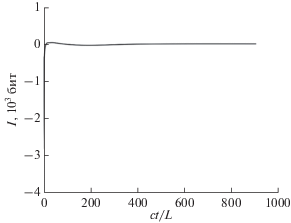
Рис. 4.
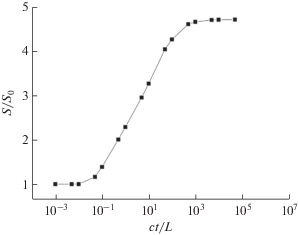
Зависимость нормы спектральной плотности, отнесенной к ее значению при t = 0, смоделированной поверхности растущей пленки согласно теории КПЖ от нормированного на размер скана времени роста.
ЗАКЛЮЧЕНИЕ
Сравнение АСМ-изображений выращенных пленок сплавов Гейслера с упрощенной моделью роста поверхности КПЖ (5) показало качественное согласие. Безусловно, на сигнал АСМ и, соответственно, на его расшифровку помимо топографии поверхности влияет еще много факторов, а именно жесткость и амплитудно-частотные характеристики системы кантилевер–поверхность, адгезионные свойства поверхности, зависящие от ее кривизны, внутренние напряжения и дефекты структуры. В рамках представленного анализа влияние этих факторов считается пренебрежимо малым, однако в перспективе планируется оценка масштаба вклада в сигнал АСМ всех этих факторов.
Значение отработки методов оценки спектрального (20) и информационного (21) функционалов, связанных с высотой растущей поверхности, состоит в следующем. Особенностью моделей вида (1), к которым принадлежит и рассмотренная выше модель КПЖ (5), является возможность введения в них управления $u$:
(24)
$\frac{{\partial H}}{{\partial t}} = \tilde {F}\left( {\frac{{\partial H}}{{\partial {{x}_{1}}}},\frac{{\partial H}}{{\partial {{x}_{2}}}},\frac{{{{\partial }^{2}}H}}{{\partial x_{1}^{2}}},\frac{{{{\partial }^{2}}H}}{{\partial {{x}_{1}}\partial {{x}_{2}}}},\frac{{{{\partial }^{2}}H}}{{\partial x_{2}^{2}}}, \ldots ;u} \right),$Для уравнения (24) целесообразно выбрать пространство состояний – функциональное пространство, для того чтобы рассматривать в нем это уравнение как бесконечномерную динамическую систему. Наиболее удобным выбором является банахово пространство ${{L}^{p}}({{\Omega }_{0}})$ c нормой:
(25)
${{\left\| H \right\|}_{p}} = {{\left[ {\int\limits_{{{\Omega }_{0}}} {{{{\left| {H({\mathbf{x}},t)} \right|}}^{p}}} {{d}^{2}}x} \right]}^{{\frac{1}{p}}}},\,\,\,\,1 \leqslant p < \infty .$Управление $u({\mathbf{x}},t)$ можно считать элементом банахова пространства $L_{m}^{p}({{\Omega }_{0}})$ с нормой:
(26)
${{\left\| u \right\|}_{p}} = {{\left[ {\sum\limits_{k = 1}^m {\int\limits_{{{\Omega }_{0}}} {{{{\left| {{{u}_{k}}({\mathbf{x}},t)} \right|}}^{p}}} {{d}^{2}}x} } \right]}^{{\frac{1}{p}}}},\,\,\,\,1 \leqslant p < \infty .$Рассмотрим функционал вида:
(27)
$\Phi [H,u] = \int\limits_0^\tau {\int\limits_{{{\Omega }_{0}}} {\varphi \left( {\frac{{\partial H}}{{\partial {{x}_{1}}}},\frac{{\partial H}}{{\partial {{x}_{2}}}}, \ldots ;u} \right)} } {\kern 1pt} {{d}^{2}}xdt.$В этом случае возможна постановка задачи оптимального управления распределенной системой [12]: найти функции $H \in {{L}^{p}}({{\Omega }_{0}})$ и $u \in L_{m}^{p}({{\Omega }_{0}})$ такие, что на отрезке времени $t \in [0,\tau ]$ эти функции удовлетворяют уравнению (24) и минимизируют функционал (27). Это означает, что при придании функционалу (27) ясного физического смысла открывается возможность для осуществления наноинженерии, т.е. выращивания наноструктур с заданными свойствами. В частности, в [13] был предложен следующий функционал:
(28)
$\int\limits_{{{\Omega }_{0}}} {{{{[H({\mathbf{x}},\tau ) - {{H}_{*}}({\mathbf{x}})]}}^{2}}} {{d}^{2}}x \to \min ,$Однако для практической реализации наноинженерии в каждом конкретном случае в первую очередь необходимо верифицировать уравнение (1), т.е. убедиться, что для каждого конкретного материала формирование неоднородного рельефа поверхности кристалла идет согласно этому уравнению с соответствующей данному материалу и физическому процессу функцией $F( \ldots ).$ Для формализации процедуры верификации рассмотрим вектор-функцию:
Введем в пространстве вектор-функций (29) норму
(30)
${{\left\| {\mathbf{Q}} \right\|}_{p}} = {{\left[ {\int\limits_0^\tau {\left( {\sum\limits_{j = 1}^3 {{{{\left| {{{Q}_{j}}(t) - {{{\tilde {Q}}}_{j}}(t)} \right|}}^{p}}} } \right)dt} } \right]}^{{\frac{1}{p}}}},\,\,\,\,1 \leqslant p < \infty $Подчеркнем, что включение в векторный критерий качества функционала, характеризующего фрактальность поверхности, обусловлено обработкой результатов эксперимента. Ранее это обстоятельство привело к рассмотрению в [5] процессов рассеяния электронов на фрактальных поверхностях эпитаксиальных металлических пленок и ферромагнитных наноструктур. Более того, в [14] на основе изучения АСМ-изображений поверхностей для целого ряда образцов конструкционных материалов, подвергнутых типовым процессам физико-химической обработки, таким как микродуговое оксидирование, алмазное шлифование, однозначно показано, что исследованные поверхности являются фрактальными. Таким образом, фрактальность в физике поверхности является правилом, а не исключением.
В векторный критерий качества могут быть включены не только величины, связанные с АСМ, но и результаты других возможных, не повреждающих поверхность измерений. Так, в [15] рассматривали не только АСМ-измерения, но данные рассеяния света на поверхности образца. Интегралы (20) и (21) можно вычислять не только по формулам прямоугольных параллелепипедов (22) и (23), но и с помощью более точных кубатурных формул [16]. Освоение таких продвинутых численных алгоритмов открывает дорогу к верификации нелокальных моделей эволюции поверхности [17, 18] на суперЭВМ экзафлопсной производительности [19].
Список литературы
Nakatani T.M., Hase N., Goripati H.S. et al. // IEEE Trans. Magn. 2012. V. 48. № 5. P. 1751.
Горай Л.И., Лубов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2014. № 5. С. 39.
Кудряшов Н.А., Рябов П.Н., Стриханов М.Н. // Ядерная физика и инжиниринг. 2010. Т. 1. № 2. С. 151.
Kardar M., Parisi G., Zhang Y.C. // Phys. Rev. Lett. 1986. V. 56. P. 889.
Фомин Л.А., Маликов И.В., Винниченко В.Ю. и др. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2008. № 2. С. 27.
Fomin L.A., Malikov I.V., Pyatkin S.V., Mikhailov G.M. // J. Magn. Magn. Mater. 2010 V. 322. P. 851.
Paccaдин А.Э., Степанов А.В., Фомин Л.А. // Adv. Sci. 2018. № 1. Р. 28.
Гурбатов С.Н., Руденко О.В., Саичев А.И. Волны и структуры в нелинейных средах без дисперсии. Приложения к нелинейной акустике. М.: ФИЗМАТЛИТ, 2008. 496 с.
Стечкин С.Б., Субботин Ю.Н. Сплайны в вычислительной математике. М.: Наука, 1976. 248 с.
Rassadin A.E., Stepanov A.V., Fomin L.A. Peculiarities of Evolution of Regularized Fractal Shapes on Surface of Solid State in the Vicinity of Gradient Catastrophe // Book of Abstr. Int. Conf.-School “Dynamics, Bifurcations and Chaos 2018 (DBC V)”. Nizhny Novgorod, 2018. P. 30.
Потапов А.А., Гуляев Ю.В., Никитов С.А. и др. Новейшие методы обработки изображений / Ред. Потапов А.А. М.: ФИЗМАТЛИТ, 2008. 496 с.
Фурсиков А.В. Оптимальное управление распределенными системами. Теория и приложения. Новосибирск: Научная книга, 1999. 352 с.
Rassadin A.E., Sazanova T.S., Stepanov A.V., Fomin L.A. // IOP Conf. Ser.: Mater. Sci. Eng. 2018. V. 443. № 1. P. 012027.
Потапов А.А., Булавкин В.В., Герман В.А., Вячеславова О.Ф. // ЖТФ. 2005. Т. 75. № 5. С. 28.
Rassadin A.E. // IOP Conf. Ser.: Mater. Sci. Eng. 2019. V. 699. P. 012039.
Мысовских И.П. Интерполяционные кубатурные формулы. М.: Наука, 1981. 336 с.
Рудый А.С., Куликов А.Н., Куликов Д.А., Метлицкая А.В. // Микроэлектроника. 2014. Т. 43. № 4. С. 282.
Куликов А.Н., Куликов Д.А. // Математическое моделирование. 2016. Т. 28. № 3. С. 33.
Ким А.К., Перекатов В.И., Фельдман В.М. // Вопросы радиоэлектроники. 2018. № 2. С. 6.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования