Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 5, стр. 67-73

ВВЕДЕНИЕ

В основе атомно-силовой микроскопии (АСМ) [1] лежит измерение силы взаимодействия зонд–образец. Когда зонд АСМ-кантилевера находится в контакте с образцом, можно, подняв образец на известную высоту, определить угол изгиба кантилевера, линейно связанный с вертикальной компонентой силы [2]. Часто важны все три компоненты силы, например, для манипуляций слабо закрепленными на подложке частицами [3, 4], измерений формы трехмерных объектов [5], исследований пьезоотклика сегнетоэлектрических образцов [6, 7], точных наномеханических экспериментов [8–10]. Приложенная к зонду сила вызывает реакцию кантилевера, которую можно контролировать, регистрируя в выбранной на нем точке механические напряжения пьезорезистивным методом [11–13], углы изгиба и кручения методом оптического рычага [14], вертикальное смещение методом интерферометрии [15]. Комбинируя методы интерферометрии и оптического рычага, можно по смещению и углу изгиба кантилевера определить компоненты силы в плоскости изгиба, а по углу кручения – компоненту, перпендикулярную этой плоскости. Все проекции силы поддаются измерению также при помощи комбинации метода оптического рычага и пьезорезистивного метода.

Метод интерферометрии и пьезорезистивный метод не чувствительны к компоненте силы, перпендикулярной плоскости изгиба. Автономно определить вектор силы целиком позволяет только метод оптического рычага, примененный в двух точках на кантилевере. В [16, 17] обсуждали оптимальное положение этих точек для минимальной ошибки измерений. Было доказано [17], что первое положение совпадает с проекцией вершины зонда на консоль, другое зависит от направления и амплитуды проекции силы на плоскость изгиба консоли и рассчитывается аналитически.

Для практики важно существование зафиксированных на кантилевере оптимальных положений точек для определения компонент произвольно направленной силы. В этой связи в настоящем исследовании при использовании подхода [17] сопоставлены разные комбинации методов пьезорезистивного, оптического рычага, интерферометрии. Специально для этого рассчитаны и проанализированы положения оптимальных точек на кантилевере – одной при сочетании двух методов и двух при использовании одного метода – как функции направления и амплитуды приложенной к зонду силы.

РЕЗУЛЬТАТЫ

АСМ-кантилевер – это консоль длиной l_C с зондом высотой l_T (рис. 1a). Если к кончику зонда приложить силу F, то ее компоненты F_Y и F_Z изогнут, а компонента F_X закрутит консоль [18]. Форма слабого изгиба [19] консоли в плоскости YZ подчиняется уравнению Эйлера–Бернулли:

Левая часть (1) – это произведение модуля Юнга E материала консоли, момента инерции I = = wt ³/12 ее прямоугольного сечения шириной w и толщиной t, локальной кривизны Z  ''(Y); правая часть – распределение момента сил, линейная функция координаты Y вдоль консоли (рис. 1а).

Пьезорезистивным методом (ПР) регистрируется связанная с механическим напряжением локальная деформация консоли, следовательно, ее кривизна, пропорциональная моменту сил и при малых изгибах приближенно равная второй производной смещения; методом оптического рычага (ОР) – первообразная кривизны, угол изгиба α; методом интерферометрии (И) – первообразная угла, смещение (величина изгиба) консоли (рис. 1б). Можно записать:

Переменная z и координата x = Y/l_C, x ∈ [0; 1], безразмерны. Использованы жесткость k_C = = ${{Ew{{t}^{3}}} \mathord{\left/ {\vphantom {{Ew{{t}^{3}}} {(4l_{C}^{3})}}} \right. \kern-0em} {(4l_{C}^{3})}}$ прямоугольной консоли, пьезорезистивный коэффициент Π, вариация ∆R₀(x)/R₀ сoпротивления пьезодатчика [11].

Из (1) и (2), также из рис. 1, следует:

|F_YZ| и α^F – это амплитуда и полярный угол проекции приложенной силы в плоскости изгиба консоли YZ. Если пренебречь деформацией зонда, можно в (3a) заменить F_Y и F_Z на Y ^C и Z ^C, компоненты смещения “идеального” кантилевера r^C [20]: где $\left| {{\mathbf{r}}_{{YZ}}^{C}} \right|$ и α^r – это амплитуда и полярный угол проекции вектора смещения “идеального” кантилевера на плоскость изгиба консоли (рис. 1а).

В (3а) a^F и b^F зависят от силы, а в (3б) a^r и b^r – от смещения, но a = a^F = a^r и b = b^F = b^r. Чтобы рассчитать a и b, достаточно из трех величин z, z', z'' определить две в одной точке либо одну в двух точках на консоли. Положения таких точек можно выбрать оптимальным образом.

Найдем в качестве примера две оптимальные точки определения z'' пьезорезистивным методом. Обозначив z''(x) = p, выразим параметры a и b через измеряемые величины x_i и p_i:

Ошибки определения, дисперсии a и b, $\sigma _{a}^{2}$ и $\sigma _{b}^{2},$ зависят от дисперсий x_i и p_i. Используя (4), минимизируем линейную комбинацию $\sigma _{a}^{2}$ и $\sigma _{b}^{2}$ в области x₁, x₂ ∈ [0; 1]: Введены k = σ_p/σ_x – отношение ошибок измерений нормированных локальной кривизны консоли p = z '' и координаты x (рис. 1а), служебный параметр θ. В зависимости от величины θ значимы, например, только $\sigma _{a}^{2}$ при cos  θ = 1, только $\sigma _{b}^{2}$ при sin θ = 1, обе ошибки при cos θ = sin θ [17].

Из (4) и (5) получаем:

Введя переменные g, h ∈ [0; 1], g = (2x₁x₂)^1/2 и h = = x₁ – x₂, перепишем (6): M(g, h) для любого фиксированного h ∈ (0; 1] как возрастающая функция g минимальна при g = 0. M(g, h) для любого фиксированного g ∈ [0; 1] как убывающая функция h минимальна при h = 1. Поэтому M(g, h) имеет минимум в точке g = 0, h = 1, а M(x₁, x₂) – в x₁ = 1, x₂ = 0. Важно, что решение не зависит от k, b, a, θ. С учетом (3a) и (3б) это означает независимость от направления, амплитуды силы (или вектора смещения) и точности измерений x и z''.

Стоит подчеркнуть, что приведенный выше результат строго обоснован: точнее всего коэффициенты зависимости p = a – bx определяются, если измерить p на краях отрезка [0; 1]. Благодаря этому для оптимизации пьезорезистивного метода есть универсальное решение: один пьезодатчик следует расположить там, где консоль закреплена, а другой – на свободном конце, т.е. в x_2extr = 0 и x_1extr = 1 (рис. 2г, 3г).

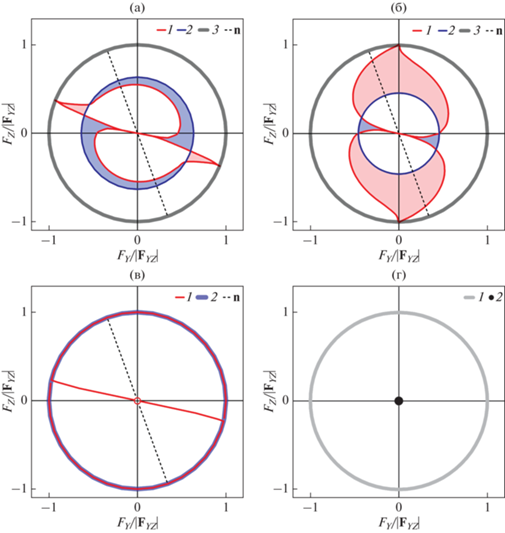
В [17] для метода оптического рычага было доказано: при любых k, b, a, θ одна из координат минимума M(x₁, x₂) – это x_1extr = 1. Это верно также для метода интерферометрии, что доказывается аналогично [17]. Вторая координата x_2extr в случае методов интерферометрии и оптического рычага и координата x_extr для комбинаций И + ОР, И + ПР, ОР + ПР определяется по корню полинома из табл. 1. В [17] представлен подробный аналитический вывод коэффициентов такого полинома и продемонстрировано согласие результатов расчетов для метода оптического рычага с АСМ-измерениями.

На рис. 2 для различных комбинаций методов показаны угловые диаграммы оптимальных точек минимума ошибки измерений компонент F. В отличие от диаграммы x_1extr(α^F) = 1 форма диаграмм x_2extr(α^F) и x_extr(α^F) зависит от безразмерного параметра C^F = kk_Cl_C/|F_YZ| (подробно о параметре написано в [17]).

Рассмотрим на рис. 2а диаграммы метода интерферометрии. Две концентрические окружности x_1extr = 1, 3, и x_2extr ≈ 0.63 с C ^F → ∞ (кривая 2) – это изотропные диаграммы, а диаграмма x_2extr(α^F) (кривая 1) рассчитана для C ^F = 0 и анизотропна. Так как в эксперименте C ^F ~ 1 [17], диаграмма x_2extr для оптимизации АСМ-измерений лежит в закрашенных областях между 1 и 2 и тоже будет анизотропной. Пунктирный диаметр на рис. 2а под углом α^F = 110° соответствует вертикальной оси N на рис. 1а, вдоль которой реакция опоры (т.е. сила со стороны плоского образца в отсутствие трения) действует на зонд. В этом случае оптимальные измерения будут в x_1extr = 1 и x_2extr ∈ [0.56; 0.63] (рис. 2а, участки диаметра n в закрашенных областях между анизотропной и изотропной диаграммами 2 и 1).

Таким же путем по пересечениям диаметра n с диаграммами 2 и 1 на рис. 2б для метода оптического рычага получим более широкий диапазон x_2extr ∈ [0.46; 0.88], а диаграмма для комбинаций методов (рис. 2в) в случае реакции опоры дает не зависящее от C ^F, фиксированное значение x_extr = 1. Аналогично ищутся оптимальные точки измерений для других направлений силы.

На практике измерять вектор произвольно направленной силы удобней, имея изотропные диаграммы оптимальных точек, как на рис. 2г в пьезорезистивном методе. На рис. 2в диаграмма 2 с C^F → ∞ – это окружность x_extr = 1. Диаграмма с конечным C^F ≥ 0 отличается от этой окружности только в двух диаметрально противоположных узких диапазонах α^F шириной ≈ 0.5° (OР + ПР), 1.3° (И + ПР), 2.1° (И + ОР). Общие границы диапазонов дает условие a = 0 в (3а) (F_Z = –λF_Y): α^F ≈ ≈  –11.3° и 168.7° для λ = 0.2. На границе x_extr = 1, если C ^F > 0, и x_extr не определено, если C ^F = 0 (выколотая точка в центре координат на рис. 2в). Комбинации методов упорядочиваются с учетом широты угловых диапазонов, где x_extr зависит от C ^F, и площади областей между диаграммами на рис. 2а, 2б, где от C ^F зависит x_2extr. В итоге имеем: ПР, И + ОР, И + ПР, ОР + ПР, И, ОР.

На рис. 3 показаны диаграммы оптимизации измерений компонент вектора смещения r^C “идеального” кантилевера. В соответствующих друг другу случаях на рис. 2 и 3 отличия формы диаграмм объясняются несовпадением углов α^r и α^F. Из выражений (3а) и (3б) следует связь между этими углами [17]:

Например, диаметры n на рис. 2а–2в соответствуют диаметрам s на рис. 3а–3в. Вертикаль n идет под углом α^F ≈ 110° к горизонтальной оси, а направление скольжения s согласно (8) для λ = 0.2 – под углом α^r ≈ 74°.

Диаграммы с конечным C ^r ≥ 0 будут отличаться от окружности x_extr = 1 с C ^r → ∞ (рис. 3в) в диаметрально противоположных диапазонах углов α^r: ≈ 7° (OР + ПР), ≈ 23° (И + ПР), ≈ 117° (И + ОР). Общие границы диапазонов дает условие a = 0 в системе (3б): α^r ≈ 59° и ≈ 239° для λ = 0.2. Эти диапазоны шире своих аналогов, рассмотренных при обсуждении рис. 2в, но три пары методов упорядочиваются так же, как в случае измерений вектора силы.

ЗАКЛЮЧЕНИЕ

Комбинируя методы пьезорезистивный, оптического рычага и интерферерометрии попарно в одной точке либо любой из них в двух точках на консоли, можно измерять компоненты силы взаимодействия АСМ-зонд–образец в плоскости изгиба консоли, а в трех комбинациях с методом оптического рычага – вектор силы целиком. В пяти комбинациях методов, соответствующих минимуму ошибки измерений, оптимальные положения таких точек меняются c направлением силы и, соответственно, смещением “идеального” кантилевера с “недеформируемым” зондом [17, 20]. Можно выстроить эти комбинации по возрастанию изменчивости положений оптимальных точек: И + ОР, И + ПР, ОР + ПР, И, ОР. У пьезорезистивного метода оптимальные точки, не зависящие от амплитуды и направления как приложенной к зонду силы, так и смещения “идеального” кантилевера, зафиксированы в месте крепления и на свободном конце консоли. Однако по сравнению с пьезорезистивным методом, методы оптического рычага и интерферометрии чувствительны к меньшим силам [13]. Поэтому при реализации измерений в АСМ векторов силы и смещения зонда выбор может быть сделан в пользу комбинаций И + ОР в одной точке [21] и оптического рычага в двух точках [16, 17].