Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 5, стр. 37-41
Компьютерное моделирование фазовых переходов в трехмерных слабо разбавленных спиновых системах
А. К. Муртазаев a, А. Б. Бабаев b, *
a Институт физики им. Х.И. Амирханова Дагестанский федеральный исследовательский центр
Российской академии наук
367010 Махачкала, Россия
b Дагестанский федеральный исследовательский центр РАН
367032 Махачкала, Россия
* E-mail: b_albert78@mail.ru
Поступила в редакцию 16.06.2021
После доработки 27.08.2021
Принята к публикации 30.08.2021
- EDN: KNEAJE
- DOI: 10.31857/S1028096022050156
Аннотация
Проведено компьютерное моделирование фазовых переходов в трехмерной слабо разбавленной модели Поттса с числом состояний спина q = 5 на простой кубической решетке. Расчеты проводились для спиновых систем с периодическими граничными условиями при концентрации спинов p = 1.0 и p = 0.90. При этом рассматривались системы с линейными размерами L × L × L = N, L = 10–80. Получены температурные зависимости теплоемкости, восприимчивости и намагниченности в зависимости от линейных размеров изучаемых систем L. Методом кумулянтов Биндера четвертого порядка и с применением гистограммного анализа данных показано, что наличие слабого беспорядка в виде немагнитных примесей порядка с = 10% (с = 1 – p, p – концентрация спинов) не сказывается на фазовом переходе первого рода.
ВВЕДЕНИЕ
Фазовые переходы (ФП) и связанные с ними критические явления (КЯ) чрезвычайно широко распространены в конденсированных средах. При определенных условиях во всех конденсированных средах происходят один или несколько фазовых переходов. На разработку эффективной теории ФП и КЯ были затрачены значительные усилия, и к настоящему моменту времени в этом направлении достигнут существенный прогресс [1–3]. С другой стороны, следует отметить, что большинство результатов в этой области получены для однородных, идеализированных и сильно упрощенных моделей. В реальном мире мы имеем дело со спиновыми системами и материалами, которые существенно отличаются от идеализированных систем. Как с точки зрения практики, так и с точки зрения теории, всегда возникает вопрос о влиянии дефектов и случайных структур, присутствующих в реальных системах, на различные тепловые и магнитные характеристики. В этом плане особенный интерес представляет определение трикритической точки pс, отделяющей на фазовой диаграмме область ФП первого рода от области ФП второго рода [4, 5]. Кроме того, возникает вопрос уверены ли мы в том, что ФП первого рода наблюдаются в присутствии разбавления? Точная величина pс имеет большое значение при создании различных новых магнитных материалов, а также при изучении высоко температурной сверхпроводимости, возникающей при замещении небольшого количества магнитных атомов La немагнитными атомами стронция Sr в антиферромагнитном диэлектрике LaCuO4 [6].
МОДЕЛЬ И МЕТОД ИССЛЕДОВАНИЯ
В узлах i кубической решетки L × L × L с периодическими граничными условиями расположены спины ${{S}_{i}},$ которые могут находиться в одном из следующих состояний q = 1, 2, 3, 4, 5, и немагнитные примеси (Si = 0). Немагнитные примеси неподвижны. Энергия связи между двумя узлами равна нулю, если хотя бы в одном узле находится немагнитная примесь или, если взаимодействующие спины находятся в различных состояниях, и равна J, если оба узла заняты магнитными атомами, находящимися в одинаковых состояниях. Гамильтониан такой системы можно записать в следующем виде [7]:
(1)
$H = - \frac{1}{2}J\sum\limits_{i,j} {{{\rho }_{i}}{{\rho }_{j}}\delta {\kern 1pt} {\text{(}}{{S}_{i}}{\text{,}}{{S}_{j}}{\text{)}}} ,\,\,\,\,{{S}_{i}} = 1,2,3,4,5,$и J – параметр обменного ферромагнитного взаимодействия ближайших соседей (в дальнейшем считаем J = 1 и работаем с безразмерной температурой). Концентрация магнитных атомов определяется суммированием всех состояний атомов во всех узлах решетки:
(2)
$p = \frac{{\left( {{{N}_{1}} + {{N}_{2}} + {{N}_{3}} + {{N}_{4}} + {{N}_{5}}} \right)}}{{{{L}^{3}}}},$Исследования проводили на основе высокоэффективного кластерного алгоритма Вольфа метода Монте-Карло (МК) [8]. Расчеты проводили для систем с периодическими граничными условиями при концентрациях спинов р =1.00, 0.90. Начальные конфигурации задавались таким образом, чтобы все спины были упорядочены вдоль оси Z. Для вывода системы в равновесное состояние отсекался неравновесный участок длиной τ0 для системы с линейными размерами L. Этот неравновесный участок отбрасывали. Затем усреднение проводилось по участку марковской цепи длиной τ = 150τ0. Для самой большой системы L = 80, ${{\tau }_{0}} = 2.3 \times {{10}^{3}}$ МК шагов/спин. Кроме того, проводилось усреднение по различным начальным конфигурациям. В случае p = 1.0 для усреднения использовалось 15 начальных конфигураций. Для слабо разбавленных систем с концентрацией спинов p = 0.90 осуществлялось конфигурационное усреднение по 2000 различным конфигурациям, причем для каждой примесной конфигурации выполнялось усреднение по длине цепи τ = 150τ0.
РЕЗУЛЬТАТЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
Наблюдение за температурным ходом поведения теплоемкости и восприимчивости осуществлялось с использованием флуктуационных соотношений [9]:
(3)
$C = (N{{K}^{2}})\left( {\left\langle {{{U}^{2}}} \right\rangle - {{{\left\langle U \right\rangle }}^{2}}} \right),$(4)
$\chi = (NK)\left( {\left\langle {m_{F}^{2}} \right\rangle - {{{\left\langle {{{m}_{F}}} \right\rangle }}^{2}}} \right),$(5)
${{m}_{F}} = \frac{{\left[ {q\left( {\frac{{{{N}_{{\max }}}}}{N}} \right) - 1} \right]}}{{q - 1}},$На рис. 1, 2 представлены характерные зависимости восприимчивости χ и теплоемкости C от температуры T для трехмерной слабо разбавленной ферромагнитной модели Поттса c числом состояний спина q = 5 на простой кубической решетке для систем с линейными размерами L = 10–80 при концентрации спинов p = 0.90. Здесь и далее на всех рисунках погрешность данных не превышает размеров символов, используемых для построения графиков. Отметим, что в зависимости восприимчивости χ и теплоемкости C от температуры для всех исследуемых нами систем проявляются четко выраженные максимумы, и эти максимумы (в пределах погрешности) приходятся на одну температуру. Как видно из этих рисунков, представленные температурные зависимости восприимчивости и теплоемкости проявляют слабую размерную зависимость. Это связано с тем, что на исследуемую разбавленную систему накладывались периодические граничные условия. Кроме того, в рассматриваемой неупорядоченной модели Поттса с q = 5 наблюдается слабо выраженный фазовый переход первого рода, при этом размерные эффекты ярко не проявляются.
Рис. 1.
Температурная зависимость восприимчивости χ для трехмерной слабо разбавленной модели Поттса с q = 5.
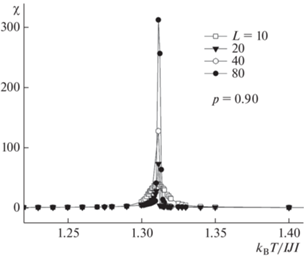
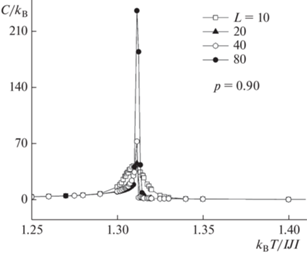
Рис. 2.
Температурная зависимость теплоемкости С для трехмерной слабо разбавленной модели Поттса с q = 5.
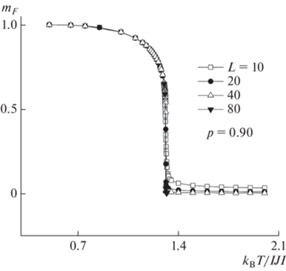
На рис. 3 представлены температурные зависимости намагниченности mF для трехмерной слабо разбавленной модели Поттса при p = 0.90. Как видно из рис. 3, наблюдается монотонное уменьшение величины mF c ростом температуры и заметное уменьшение высокотемпературных “хвостов” при увеличении линейного размера L.
Рис. 3.
Температурная зависимость намагниченности mF для трехмерной слабо разбавленной модели Поттса с q = 5.
В случае компьютерного моделирования фазовых переходов при определении температуры ФП TL наилучшим образом зарекомендовал метод кумулянтов Биндера четвертого порядка [11]:
(6)
${{V}_{L}}(T,p) = 1 - \frac{{{{{\left\langle {{{E}^{4}}(T,p;L)} \right\rangle }}_{L}}}}{{3\left\langle {{{E}^{2}}(T,p;L)} \right\rangle _{L}^{2}}},$(7)
${{U}_{L}}(T,p) = 1 - \frac{{{{{\left\langle {{{m}^{4}}(T,p;L)} \right\rangle }}_{L}}}}{{3\left\langle {{{m}^{2}}(T,p;L)} \right\rangle _{L}^{2}}},$Рис. 4.
Температурная зависимость кумулянтов Биндера VL(T, p) для трехмерной слабо разбавленной модели Поттса при p = 0.90.
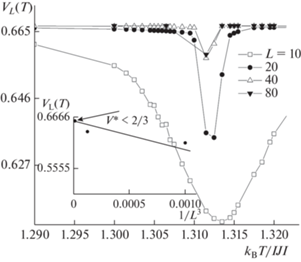
Рис. 5.
Температурная зависимость кумулянтов Биндера UL(T, p) для трехмерной слабо разбавленной модели Поттса при p = 0.90.

Параллельно с методом кумулянтов Биндера для анализа рода ФП нами использовался и гистограммный анализ данных метода Монте-Карло [17, 18]. Гистограммный анализ данных, проведенный нами для трехмерной слабо разбавленной ферромагнитной модели Поттса с числом состояний спина q = 5 на простой кубической решетке, также свидетельствует о наличии ФП первого рода. Это продемонстрировано на рис. 6. На данном рисунке представлена гистограмма распределения энергии вблизи точки фазового перехода TL для систем с линейным размером L = 80 при концентрации спинов p = 0.90. Как видно из вставки на рис. 6, наблюдается бимодальность в распределении энергии, характерная для ФП первого рода. Для этой модели при концентрации спинов p = 0.8 в работе [19] было выявлено распределение энергии с одним максимумом. По-видимому, трикритическая точка для трехмерной модели Поттса с q = 5 находится в интервале изменения концентраций спинов 0.80 < pc < 0.9. Определение точного значения трикритической точки pc требует отдельного рассмотрения. Значение pc также зависит от числа состояний спина q рассматриваемой модели Поттса. В частности, в трехмерной модели Поттса с числом состояний спина q = 3 наличие незначительных количества немагнитных примесей (порядка 5%) оказывается существенным, при этом происходит смена фазового перехода первого рода на фазовый переход второго рода [20].
Рис. 6.
Гистограмма распределения энергии для трехмерной слабо разбавленной модели Поттса с q = 5 при p = 0.90.

Таким образом, полученные в результате наших исследований данные свидетельствуют о том, что в трехмерных структурах, описываемых ферромагнитной моделью Поттса с q = 5 на простой кубической решетке, слабый беспорядок, реализованный в виде немагнитных примесей концентрацией 10%, не оказывается существенным, и в рассматриваемой спиновой системе наблюдается фазовый переход первого рода, как и в случае однородной модели Поттса.
ЗАКЛЮЧЕНИЕ
В данной работе с соблюдением единой методики исследованы фазовые переходы в трехмерной слабо разбавленной ферромагнитной модели Поттса с числом состояний спина q = 5 на простой кубической решетке методами компьютерного моделирования. С использованием кумулянтов Биндера четвертого порядка определены температуры фазового перехода в зависимости от концентрации спинов p. Показано, что температурные зависимости для намагниченности, теплоемкости и восприимчивости не проявляют конечно-размерные эффекты. Полученные данные на основе вычислительного эксперимента свидетельствуют о том, что в рассматриваемой модели Поттса внесение небольшого беспорядка в виде немагнитных примесей в количестве c = 10% (с = = 1 – p) каноническим способом не существенно для фазового перехода первого рода.
Список литературы
Паташинский А.З., Покровский В.А. Флуктуационная теория фазовых переходов, М.: Наука, 1982. 154 с.
Прудников В.В., Вакилов А.Н., Прудников П.В. Фазовые переходы и методы их компьютерного моделирования, М.: Физматлит, 2009. 254 с.
Henkel M., Pleimling M., Nonequilibtium Phase Transitions, Springer, 2010. P. 320.
Cardy J., Jacobsen J.L. // Phys. Rev. Lett. 1997. V. 79. P. 4063.
Fernandez L.A., Gordillo-Guerrero A., Martin-Mayor V., Ruiz-Lorenzo J.J. // Phys. Rev. B. 2012. V. 86. P. 184428.https://doi.org/10.1103/PhysRevB.86.184428
Sen C., Alvarez G., Dagotto E. // Phys. Rev. Lett. 2007. V. 98. P. 127202.
Wu F.Y. Exactly Solved Models. London: World Scientific, 2009.
Wolff U. // Phys. Lett. 1989. V. 62. P. 361. https://doi.org/10.1103/PhysRevLett.62.361
Peczac P., Ferrenberg A.M., Landau D.P. // Phys. Rev. B. 1991. V. 43. P. 6087. https://doi.org/10.1103/PhysRevB.43.6087
Chatelain C., Berche B. // Phys. Rev. Lett. 1998. V. 80. P. 1670. https://doi.org/10.1103/PhysRevLett.80.1670
Eichhorn K., Binder K. // J. Phys.: Condens. Matter. 1996. V. 8. P. 5209. https://doi.org/10.1088/0953-8984/8/28/005
Murtazaev A.K., Babaev A.B. // Journal of Surface Investigation: X-ray, Synchrotron and Neutron Techniques. 2020. V. 14. № 4. P. 727. https://doi.org/10.1134/S1027451020030350
Murtazaev A.K., Babaev A.B. // Physics of the Solid State. 2020. V. 62. № 5. P. 851. https://doi.org/10.1134/S1063783420050042
Murtazaev A.K., Babaev A.B. // Materials Letters. 2020. V. 258. P. 126771. https://doi.org/10.1016/j.matlet.2019.126771
Babaev A.B., Murtazaev A.K. // Low Temperature Physics. 2020. V. 46. P. 688. https://doi.org/10.1063/10.0001365
Murtazaev A.K., Babaev A.B., Ataeva G.Ya. // Physics of the Solid State. 2020. V. 62. № 7. P. 1228. https://doi.org/10.1134/S1063783420070185
Alves N.A., Berg B.A., Villanova R. // Phys. Rev. B. 1990. V. 41. P. 383. https://doi.org/10.1103/PhysRevB.41.383
Wang F., Landau D.P. // Phys. Rev. E. 2001. V. 64. P. 056101. https://doi.org/10.1103/PhysRevE.64.056101
Murtazaev A.K., Babaev A.B. // J. Experimental and Theoretical Physics. 2021. V. 132. P. 917. https://doi.org/10.1134/S1063776121060054
Babaev A.B., Murtazaev A.K. // Low Temperature Physics. 2015. V. 41. P. 608. https://doi.org/10.1063/1.4929595
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


