Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 6, стр. 34-46
Кинетические явления в полупроводнике, возбуждаемом ориентированным пучком быстрых частиц
a Национальный исследовательский ядерный университет “МИФИ”
115409 Москва, Россия
b Национальный исследовательский центр “Курчатовский институт”
123122 Москва, Россия
* E-mail: eugen_mazur@mail.ru
Поступила в редакцию 17.06.2021
После доработки 14.08.2021
Принята к публикации 20.08.2021
- EDN: BFPOLP
- DOI: 10.31857/S102809602203013X
Аннотация
Показано, что прохождение каналированных частиц сквозь кристалл без центра симметрии или в магнитном поле приводит к появлению тока – квазифотогальваническому и квазифотомагнитному эффектам. Построена теория этих явлений. Предсказана ориентационная зависимость квазифотогальванического и квазифотомагнитного тока от угла влета каналированной частицы по отношению к кристаллографическим плоскостям. Исследована зависимость эффекта от состояния и квантовых переходов каналированной частицы. Изучен вклад в квазифотомагнитный эффект матричных элементов как первого, так и второго рода. Оценена интенсивность квазифотомагнитного тока, индуцированного не дипольным излучением жестких фотонов, сгенерированным высокоэнергетической каналированной частицей.
ВВЕДЕНИЕ
В кристалле без центра симметрии воздействие электромагнитной волны вызывает ток, связанный с возникновением асимметрии распределения электронов по скоростям или сдвигом электронов в координатном пространстве при квантовых переходах [1–3]. В кристаллах с центром симметрии, очевидно, такой же эффект может возникнуть при наложении магнитного поля. При воздействии на центросимметричный кристалл импульса быстрых частиц в магнитном поле также возникает электрический ток (эффект Кикоина–Носкова [4, 5]). В отсутствие магнитного поля такой эффект проявляется в нецентросимметричных кристаллах. Для возбуждения полупроводника наиболее удобен [6, 7] пучок каналированных частиц, поскольку эффекты повреждения кристалла такими быстрыми частицами отсутствуют, а изменение энергии быстрых ориентированных заряженных частиц или их угла влета относительно кристаллографических плоскостей приводит к контролируемым изменениям уровня возбуждения кристалла и спектра генерируемых в нем возбуждений [8]. Основные представления о физике каналированных частиц изложены в [9]. В настоящей работе показано, что прохождение каналированных частиц в кристалле без центра симметрии или в магнитном поле приводит к появлению тока – квазифотогальваническому и квазифотомагнитному эффектам. Построена теория этих явлений.
ВОЗБУЖДАЕМЫЙ В КРИСТАЛЛЕ ТОК
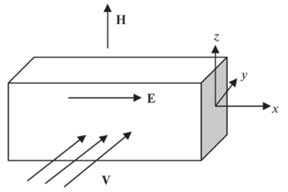
Будем рассматривать кристалл, помещенный в скрещенные электрическое E и магнитное H поля и испытывающий воздействие импульса быстрых заряженных (каналированных) частиц, движущихся в направлении, параллельном выбранным кристаллографическим плоскостям, в конфигурации, представленной на рис. 1. Для плотностей токов электронов je и дырок jh, возбуждаемых в кристалле, находящемся под воздействием магнитного и электрического полей, быстрой, ориентированной относительно кристаллографических плоскостей заряженной частицей, в работе рассматривали следующие уравнения:
(1)
${{{\mathbf{j}}}_{e}} = e{{\mu }_{e}}{{n}_{e}}{\mathbf{E}} + e{{D}_{e}}{\text{grad}}{{n}_{e}} - {{\mu }_{{{\text{H}}e}}}\left[ {{{{\mathbf{j}}}_{e}} \times {\mathbf{B}}} \right],$(2)
${{{\mathbf{j}}}_{h}} = e{{\mu }_{h}}{{n}_{h}}{\mathbf{E}} - e{{D}_{h}}{\text{grad}}{{n}_{h}} + {{\mu }_{{{\text{H}}h}}}\left[ {{{{\mathbf{j}}}_{h}} \times {\mathbf{B}}} \right],$(3)
$\frac{{\partial {{n}_{e}}}}{{\partial t}} = {{G}_{e}} - {{R}_{e}} + \frac{1}{e}{\text{div}}{\kern 1pt} {{{\mathbf{j}}}_{e}},$МАТРИЦА ПЛОТНОСТИ ВОЗБУЖДЕННОГО КРИСТАЛЛА
Общее выражение для плотности тока j в макроскопической пространственно однородной электронно-фононной системе кристалла, описываемой неравновесной матрицей плотности $\hat {\rho },$ имеет вид:
где ${\mathbf{\hat {V}}}$ – оператор скорости электронов кристалла, ${{\hat {\rho }}_{e}}$ – матрица плотности электронов в кристалле. Общее выражение для тока j (5) распадается на вклады диагональных элементов матрицы плотности электронов, т.е. функций распределения ${{f}_{{p \equiv }}}{{\hat {\rho }}_{{pp}}}{\text{:}}$(6)
$\begin{gathered} {{{\mathbf{j}}}_{{{\text{диаг}}}}} = e\int {{{d}^{3}}p} \left( {{{{({\mathbf{\hat {V}}})}}_{{pp}}}{{{\hat {\rho }}}_{{pp}}}} \right) = \\ = e\int {{{d}^{3}}p} \left( {{{{({\mathbf{\hat {V}}})}}_{{pp}}}{{f}_{p}}} \right) = \frac{{\text{l}}}{\hbar }\sum\limits_{SK} {{{f}_{{SK}}}\frac{{\partial {{\varepsilon }_{{SK}}}}}{{\partial K}}} \\ \end{gathered} $(7)
${{{\mathbf{j}}}_{{{\text{недиаг}}}}} = e\int {{{d}^{3}}p{{d}^{3}}p{\kern 1pt} '} \left( {{{{({\mathbf{\hat {V}}})}}_{{pp{\kern 1pt} '}}}{{{\hat {\rho }}}_{{pp{\kern 1pt} '}}}} \right).$(8)
$\hat {H} = {{\hat {H}}_{{{\text{кр}}}}} + {{\hat {H}}_{{{\text{ч - кр}}}}} + {{\hat {H}}_{{\text{ч}}}} \equiv {{\hat {H}}_{1}} + {{\hat {H}}_{2}},$(13)
$i\frac{{\partial {{{\hat {\rho }}}_{1}}}}{{\partial t}} = \left[ {{{{\hat {H}}}_{0}},{{{\hat {\rho }}}_{1}}} \right] + S{{p}_{2}}\left[ {\hat {W},\hat {\rho }} \right].$(14)
$\hat {\rho }\left( t \right) = \hat {\rho }_{2}^{{\left( 0 \right)}}{{\hat {\rho }}_{1}}\left( t \right).$(15)
$\frac{{\partial {{\rho }_{{1SS{\kern 1pt} '}}}}}{{\partial t}} + i\left( {{{E}_{S}} - {{E}_{{SS{\kern 1pt} '}}}} \right){{\rho }_{{1SS{\kern 1pt} '}}} = {{I}_{{SS{\kern 1pt} '}}},$(16)
$\begin{gathered} {{I}_{{SS{\kern 1pt} '}}} = \pi \mathop \sum \limits_{S{\kern 1pt} ''S{\kern 1pt} '''} \rho _{{2\alpha }}^{{\left( 0 \right)}}\left\{ {W_{{SS{\kern 1pt} ''}}^{{\alpha {\kern 1pt} {\text{'}}\alpha }}W_{{S{\kern 1pt} '''S{\kern 1pt} '}}^{{\alpha \alpha {\kern 1pt} {\text{'}}}}} \right.{{\rho }_{{1S{\kern 1pt} ''S{\kern 1pt} '''}}}\left( t \right) \times \\ \times \,\,\left[ {\delta \left( {{{E}_{S}} + {{E}_{{\alpha {\kern 1pt} {\text{'}}}}} - {{E}_{{S{\kern 1pt} ''}}} - {{E}_{\alpha }}} \right) + } \right. \\ \left. { + \,\,\delta \left( {{{E}_{{S{\kern 1pt} '}}} + {{E}_{{\alpha {\kern 1pt} {\text{'}}}}} - {{E}_{{S{\kern 1pt} '''}}} - {{E}_{\alpha }}} \right)} \right] - \\ - \,\,\left[ {W_{{SS{\kern 1pt} ''}}^{{\alpha \alpha {\kern 1pt} {\text{'}}}}W_{{S{\kern 1pt} ''S{\kern 1pt} '''}}^{{\alpha {\kern 1pt} {\text{'}}\alpha }}{{\rho }_{{1S{\kern 1pt} '''S{\kern 1pt} '}}}\left( t \right) + W_{{S{\kern 1pt} '''S{\kern 1pt} ''}}^{{\alpha \alpha {\kern 1pt} {\text{'}}}}W_{{S{\kern 1pt} ''S{\kern 1pt} '}}^{{\alpha {\kern 1pt} {\text{'}}\alpha }}{{\rho }_{{1SS{\kern 1pt} '''}}}\left( t \right)} \right] \times \\ \left. { \times \,\,\delta \left( {{{E}_{{S{\kern 1pt} ''}}} + {{E}_{{\alpha {\kern 1pt} {\text{'}}}}} - {{E}_{{S{\kern 1pt} '''}}} - {{E}_{\alpha }}} \right)} \right\}. \\ \end{gathered} $(17)
${{{\mathbf{j}}}_{{{\text{недиаг}}}}} = {\mathbf{j}}_{{{\text{недиаг}}}}^{{{\text{phot}}}} + {\mathbf{j}}_{{{\text{недиаг}}}}^{{{\text{phon}}}} + {\mathbf{j}}_{{{\text{недиаг}}}}^{{{\text{оч}}}},$Для ${\mathbf{j}}_{{{\text{недиаг}}}}^{{{\text{оч}}}}$ в результате подстановки решения уравнения (15), усредненного по ${{\hat {\rho }}_{{{\text{ph}}}}},$ в выражение (7) получаем:
(18)
$\begin{gathered} {{{\mathbf{j}}}^{{{\text{op}}}}} = e\sum\limits_{S,\alpha } {\int {\left\{ {\left[ {\left( {{{f}_{{S{{K}_{1}}}}}{{f}_{{S{{K}_{2}}}}}} \right)\rho _{{2\alpha }}^{{\left( 0 \right)}} - {{f}_{{S{{K}_{2}}}}}\left( {1 - {{f}_{{S{{K}_{1}}}}}} \right)} \right]} \right.} } \times \\ \times \,\,W_{S}^{{\left( {{\text{op}}} \right)}}\left( {{{K}_{2}},{{K}_{1}}} \right){{R}_{S}}\left( {{{K}_{2}},{{K}_{1}}} \right) \times \\ \left. { \times \,\,\delta \left( {\Delta {{E}_{{{\text{op}}}}}\left( {{{{\mathbf{K}}}_{1}} - {{{\mathbf{K}}}_{2}}} \right)} \right) - {{\varepsilon }_{S}}\left( {{{{\mathbf{K}}}_{2}}} \right) - {{\varepsilon }_{S}}\left( {{{{\mathbf{K}}}_{1}}} \right)} \right\}d{{{\mathbf{K}}}_{1}}d{{{\mathbf{K}}}_{2}}, \\ \end{gathered} $(19)
$W_{S}^{{\left( {{\text{op}}} \right)}}\left( {{{K}_{2}},{{K}_{1}}} \right) = \frac{{{{a}^{6}}}}{{\hbar {{{\left( {2\pi } \right)}}^{5}}}}{{\left| {W_{{{{K}_{2}}{{K}_{1}}}}^{{SS}}} \right|}^{2}}.$(20)
$\int {U_{{S{\kern 1pt} '{\mathbf{K}}}}^{{\text{*}}}{{U}_{{{\text{S}}{\mathbf{K}}}}}d{\mathbf{r}}} = {{\delta }_{{SS{\kern 1pt} '}}}{{a}^{3}}.$(21)
$\begin{gathered} {{R}_{S}}\left( {{{{\mathbf{K}}}_{2}},{{{\mathbf{K}}}_{1}}} \right) = \\ = - \left( {\frac{\partial }{{\partial {{{\mathbf{K}}}_{1}}}} + \frac{\partial }{{\partial {{{\mathbf{K}}}_{2}}}}} \right){{{{\Phi }}}_{S}}\left( {{{{\mathbf{K}}}_{2}},{{{\mathbf{K}}}_{1}}} \right) + {{\Omega }_{S}}\left( {{{{\mathbf{K}}}_{2}}} \right) - {{\Omega }_{S}}\left( {{{{\mathbf{K}}}_{1}}} \right), \\ \end{gathered} $(22)
${{\Omega }_{S}}\left( {\mathbf{K}} \right) = \frac{i}{{{{a}^{3}}}}\int {U_{{S{\mathbf{K}}}}^{{\text{*}}}} \frac{\partial }{{\partial {\mathbf{K}}}}{{U}_{{S{\mathbf{K}}}}}d{\mathbf{r}}{\text{\;}}{\kern 1pt} {\text{,}}$РОЛЬ ДВУХ ФАКТОРОВ, ВЛИЯЮЩИХ НА ВОЗБУЖДЕНИЕ ТОКА
Рассмотрим относительную роль эффектов локальной неоднородности электронной плотности в кристалле с одной стороны и эффектов непрямолинейности распространения каналированных частиц в кристалле, влияющих на возбуждение квазифотогальванического тока каналированной частицей в кристалле, с другой. Такое сравнение проведем в области как надбарьерных, так и подбарьерных состояний каналированной частицы. Считая, как это обычно бывает в теории явлений каналирования, потенциал кристалла V(r) зависящим только от координаты х, отсчитываемой вдоль оси, перпендикулярной плоскостному каналу, для волновой функции ориентированной частицы $U_{p}^{{\left( n \right)}}\left( r \right)$ из [15–17] получаем уравнение
(23)
$\begin{gathered} \left( {{{\hbar }^{2}}{{\Delta }_{{xx}}} + {{E_{ \bot }^{2}} \mathord{\left/ {\vphantom {{E_{ \bot }^{2}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right)U_{{{{P}_{x}}}}^{{\left( n \right)}}\left( r \right) = \\ = {{2E} \mathord{\left/ {\vphantom {{2E} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}\sum\limits_{{{G}_{x}}} {{{V}_{{{{G}_{x}}}}}} {\text{exp}}\left( {i{{G}_{x}}x} \right)U_{{{{G}_{x}}}}^{{\left( n \right)}}\left( r \right). \\ \end{gathered} $(24)
$\begin{gathered} U_{{{{P}_{x}}}}^{{\left( n \right)}}\left( x \right) = A_{{{{P}_{x}}}}^{{\left( n \right)}}{\text{exp}}\left( {\frac{i}{\hbar }\tilde {P}_{x}^{{\left( n \right)}}x~} \right) \times \\ \times \,\,\left\{ {1 + \frac{E}{{2P_{{x0}}^{2}{{c}^{2}}}}\sum\limits_{{{G}_{{x{\kern 1pt} \ne {\kern 1pt} 0}}}} {{{{\tilde {V}}}_{{{{G}_{x}}}}}} \left( {1 + \frac{{{{P}_{{x0}}}}}{{{{G}_{x}}}}{\text{exp}}\left( {i{{G}_{x}}х} \right)} \right)~} \right\}, \\ \end{gathered} $(25)
$\begin{gathered} C_{{{{P}_{x}}}}^{{\left( n \right)}}\left( x \right) = A_{{{{P}_{x}}}}^{{\left( n \right)}}\left[ {\delta ({{P}_{{x0}}} - \tilde {P}_{x}^{{\left( n \right)}}) + } \right. \\ + \,\,\sum\limits_{{{G}_{{x{\kern 1pt} \ne {\kern 1pt} 0}}}} {\frac{{E{{{\tilde {V}}}_{{{{G}_{x}}}}}}}{{2P_{{x0}}^{2}{{c}^{2}}}}} \left( {1 + \frac{{{{P}_{{x0}}}}}{{{{G}_{x}}}}} \right) \times \\ \left. { \times \,\,~\delta \left( {{{P}_{{x0}}} - \tilde {P}_{x}^{{\left( n \right)}} - \hbar {{G}_{x}}} \right)~} \right]. \\ \end{gathered} $(26)
$\begin{gathered} \left\langle {{{U}_{{P_{x}^{'}}}}\left| {{\text{exp(}}{\kern 1pt} - {\kern 1pt} i({{q}_{x}}x + K_{x}^{'}x{\kern 1pt} '){\text{)}}} \right|U_{{{{P}_{x}}}}^{*}} \right\rangle = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \hbar }} \right. \kern-0em} \hbar }\left( {A_{{{{P}_{x}}}}^{{\left( n \right)}}A_{{\widetilde {P_{x}^{'}}}}^{{\left( {n{\kern 1pt} '} \right)}}} \right) \times \\ \times \,\,\left\{ {\delta {\kern 1pt} \left( {\frac{{\widetilde {{{P}_{x}}}}}{\hbar } - \frac{{\widetilde {P_{x}^{'}}}}{\hbar } + {{q}_{x}} + K_{x}^{'}} \right) + \frac{E}{{2P_{{x0}}^{2}{{c}^{2}}}}{\kern 1pt} \sum\limits_{{{G}_{{x{\kern 1pt} \ne {\kern 1pt} 0}}}} {\left( {{{{\tilde {V}}}_{{{{G}_{x}}}}} + {{{\tilde {V}}}_{{{{G}_{x}}}}}} \right)} \times } \right. \\ \left. { \times \,\,~\left( {1 + \frac{{{{P}_{{x0}}}}}{{{{G}_{x}}}}} \right)\delta \left( {\frac{{\widetilde {{{P}_{x}}}}}{\hbar } - \frac{{\widetilde {P_{x}^{'}}}}{\hbar } + {{q}_{x}} + K_{x}^{'} - {{G}_{x}}} \right)} \right\}. \\ \end{gathered} $(27)
$\begin{gathered} - \frac{{dE}}{{dz}} = M\int\limits_0^\infty {d\omega {\kern 1pt} {\kern 1pt} \omega } \int {\frac{{{{d}^{3}}{\mathbf{q}}}}{{{{q}^{2}}}}\delta } \left( {\omega - {\mathbf{qv}}} \right) \times \\ \times \,\,\left[ {{\text{Im}}{{\varepsilon }^{{ - 1}}}\left( {{\mathbf{q}},\omega } \right) + \sum\limits_{{{G}_{x}}{\kern 1pt} \ne {\kern 1pt} 0} {{\text{Im}}{{\varepsilon }^{{ - 1}}}} \left( {{\mathbf{q}},{{q}_{x}} + {{q}_{x}},\omega } \right)} \right] \times \\ \times \,\,\frac{2}{{MV_{0}^{2}x}}{\text{Re}}{{{\tilde {V}}}_{{{{G}_{x}}}}}\left( {1 + \frac{{{{P}_{{x0}}}}}{{{{G}_{x}}}}} \right), \\ \end{gathered} $(28)
$V\left( x \right) = \sum\limits_{{{G}_{x}}} {{\text{exp}}\left( {i{{G}_{x}}x} \right)} = {{V}_{0}} + 2\sum\limits_{{{G}_{{x{\kern 1pt} > {\kern 1pt} 0}}}} {{{V}_{{{{G}_{x}}}}}} \cos \left( {{{G}_{x}}x} \right).$(29)
$\frac{{{{\partial }^{2}}U}}{{\partial {{S}^{2}}}} + \left( {\tilde {a} - 2q\cos 2S} \right)U\left( S \right) = 0,$(30)
$\begin{gathered} \tilde {a} = \frac{{E_{ \bot }^{2}}}{{4{{G}^{2}}{{\hbar }^{2}}{{c}^{2}}}} - \frac{{8E{{V}_{0}}}}{{2{{G}^{2}}{{\hbar }^{2}}{{c}^{2}}}},\,\,\,\,q = \frac{{E{{V}_{G}}}}{{2{{G}^{2}}{{\hbar }^{2}}{{c}^{2}}}}, \\ S = 2Gx,\,\,\,\,G \equiv {{G}_{{{\text{min}}}}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {d,}}} \right. \kern-0em} {d,}} \\ \end{gathered} $(31)
$\Delta (E_{ \bot }^{2}) = 4h{{G}^{2}}{{c}^{2}}{{2}^{{4l{\kern 1pt} \, + \,{\kern 1pt} 5}}}\sqrt {\pi 2} {{q}^{{\frac{l}{2}}}}{{q}^{{0.75}}}\exp {{( - 4\sqrt q )} \mathord{\left/ {\vphantom {{( - 4\sqrt q )} {l.}}} \right. \kern-0em} {l.}}$(32)
$U_{{{{E}_{ \bot }}}}^{{\left( n \right)}}\left( x \right) = {\text{exp}}\left( {i{{\nu }_{n}}\left( {{{E}_{ \bot }}} \right)Gx} \right)D_{{{{E}_{ \bot }}}}^{{\left( n \right)}}\left( {2Gx} \right),$Рис. 2.
Зонный спектр поперечного движения ориентированного электрона в кристалле кремния как функция параметра квазиимпульса q в приближении синусоидального кристаллического потенциала. Указаны номера зон n = 1–8.

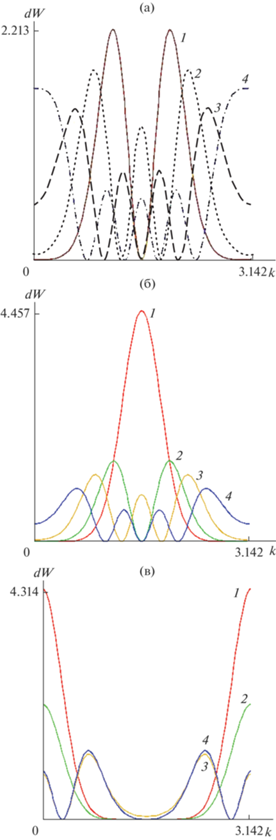
Рис. 3.
Квадрат модуля dW нечетных (а) и четных (б) волновых функций позитронов с энергией 28 МэВ в планарном канале (110) в периодическом потенциале с параметрами, соответствующими плоскости (110) в монокристалле кремния; волновой вектор k, соответствующий межплоскостному расстоянию, принят за 2π; величина волнового вектора по оси абсцисс указана в безразмерных единицах как часть межплоскостного расстояния; на рисунке показана только половина канала. Для сравнения показан квадрат модуля dW четной волновой функции электрона с этими же параметрами (в). Цифрами обозначены номера зон.
Приведем теперь точный вид коэффициентов сшивки $C_{{{{P}_{{x0}}}}}^{{\left( n \right)}}\left( {{{q}_{x}}} \right)$ в случае блоховского поведения каналированной частицы в кристалле:
(35)
$C_{{{{P}_{{x0}}}}}^{{\left( n \right)}}\left( {{{q}_{x}}} \right) = 2\pi \sum\limits_{{{G}_{x}}} {D_{{{{P}_{{x0}}}}}^{{\left( n \right)}}\left( {{{G}_{x}}} \right)\delta } \left( {\frac{{{{P}_{{x0}}}}}{h} - {{q}_{x}} + {{G}_{x}}} \right).$(36)
$\begin{gathered} \left\langle {U_{{P_{x}^{'}}}^{{*\left( n \right)}}\left| {{\kern 1pt} {\text{exp}}\left( {i{{q}_{x}}x} \right)} \right|U_{{{{P}_{x}}}}^{{\left( n \right)}}} \right\rangle = \\ = 2\pi \sum\limits_{{{G}_{x}}} {L(P_{{x,}}^{'}{{P}_{{x,}}}n{\kern 1pt} ',n,{{G}_{x}},{{q}_{x}})} \times \\ \times \,\,\delta \left( {\frac{{{{P}_{x}}}}{h} - \frac{{P_{x}^{'}}}{h} + {{q}_{x}} + {{G}_{x}}} \right). \\ \end{gathered} $В уравнении (36) символом M обозначен фурье-образ произведения модуляторов волновых функций каналированной частицы, входящих в матричный элемент
(37)
$\begin{gathered} L(P_{{x,}}^{'}{{P}_{{x,}}}n{\kern 1pt} ',n,{{G}_{x}}) = \\ = \frac{1}{{2\pi a}}\int\limits_0^a {D_{{P_{{x,}}^{'}}}^{{*\left( {n{\kern 1pt} '} \right)}}} \left( x \right)D_{{{{P}_{{x,}}}}}^{{\left( n \right)}}\left( x \right){\text{exp}}\left( { - i{{G}_{x}}x} \right)dx. \\ \end{gathered} $Подставим теперь выведенные выражения (36) и (37) в общее выражение для потерь (28) энергии на возбуждение кристалла ориентированной частицы. При этом автоматически будут учтены все типы переходов, поскольку волновая функция (28) описывает в зависимости от номера зоны n как подбарьерные, так и надбарьерные состояния. При сделанных предположениях потери энергии ориентированной частицы будут описываться следующей формулой:
(38)
$\begin{gathered} - \frac{{dE}}{{dz}} = m{{\sum\limits_{{{P}_{{x,}}}n{\kern 1pt} ',n} {\left\lfloor {C_{{{{p}_{{x0}}}}}^{{\left( n \right)}}} \right\rfloor } }^{2}} \times \\ \times \,\,\sum\limits_{{{G}_{x}}} {\int\limits_0^\infty {d\omega {\kern 1pt} {\kern 1pt} \omega } } \int {\frac{{{{d}^{3}}q}}{{{{q}^{2}}}}} {\text{Im}}{{\varepsilon }^{{ - 1}}}\left( {q,{{q}_{x}} + {{G}_{x}},\omega } \right) \times \\ \times \,\,\mathop \sum \limits_{{{K}_{x}},P_{{x,}}^{'}} L(P_{{x,}}^{'}{{P}_{{x,}}}n{\kern 1pt} ',n,{{K}_{x}})L(P_{{x,}}^{'}{{P}_{{x,}}}n{\kern 1pt} ',n,{{K}_{x}} + {{G}_{x}}) \times \\ \times \,\,\delta \left( {E - E{\kern 1pt} '\, - \hbar \omega } \right). \\ \end{gathered} $Полученные выражения (38) являются общими, поскольку в их выводе нигде не использованы какие-либо свойства волновой функции ориентированной частицы, связанные с типом выбранного приближения для кристаллического потенциала. Поведение функции (39) резко немонотонное по qx. Действительно, при qx, равных длинам векторов обратной решетки, в выражении (39) вычисление сведется к нахождению фурье-образа через рх и произведения различных функций Матье, которое обращается в нуль при Kx = 0. Эффект немонотонности квадрата модуля матричного элемента (39) в зависимости от передаваемого импульса приводит к осцилляциям квазифотогальванического тока, возбуждаемого в кристалле быстрой заряженной частицей, при изменении угла влета такой частицы по отношению к кристаллографическим плоскостям.
СОБСТВЕННЫЕ ВОЛНОВЫЕ ФУНКЦИИ
Как видим из формул (35), (38), для исследования кинетических эффектов в кристалле при прохождении ориентированной частицы необходимо знать коэффициенты заселенности состояний поперечного движения при влете частицы в кристалл, а также матричные элементы квантовых переходов ориентированной частицы Mif = $ = \left\langle {{{\psi }_{{iq}}}{\text{exp}}\left( { - i{{q}_{x}}x} \right){{\psi }_{{fq{\kern 1pt} '}}}} \right\rangle .$
Потенциал кристаллографической плоскости может быть аппроксимирован выражением вида
(40)
$V\left( x \right) - \left| {{{V}_{0}}} \right|\exp \left( {{{ - {\kern 1pt} \left| x \right|} \mathord{\left/ {\vphantom {{ - {\kern 1pt} \left| x \right|} {2R}}} \right. \kern-0em} {2R}}} \right),$(41)
$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + {{K}^{2}}} \right){{U}_{K}}\left( x \right) = 2{{E}_{K}}V\left( x \right){{U}_{K}}\left( x \right),\,\,\,\,{{K}^{2}} < 0.$(42)
${{\Psi }}_{{{{q}_{n}}}}^{{\left( e \right)}} = {{C}_{{{{q}_{n}}}}}{{J}_{{{{q}_{n}}}}}\left( {{{{{q}_{0}}{\text{exp}}\left( { - {\kern 1pt} \left| x \right|} \right)} \mathord{\left/ {\vphantom {{{{q}_{0}}{\text{exp}}\left( { - {\kern 1pt} \left| x \right|} \right)} {2R}}} \right. \kern-0em} {2R}}} \right)$(43)
$\Psi _{{{{q}_{n}}}}^{{\left( {{\text{odd}}} \right)}}(x) = {{C}_{{{{q}_{n}}}}}\left\{ {\begin{array}{*{20}{c}} {{{J}_{{{{q}_{n}}}}}\left( {{{{\text{exp}}\left( { - x} \right)} \mathord{\left/ {\vphantom {{{\text{exp}}\left( { - x} \right)} {2R}}} \right. \kern-0em} {2R}}} \right),\,\,\,\,x > 0\,} \\ {{{J}_{{{{q}_{n}}}}}\left( {{{{\text{exp}}\left( { + x} \right)} \mathord{\left/ {\vphantom {{{\text{exp}}\left( { + x} \right)} {2R}}} \right. \kern-0em} {2R}}} \right),\,\,\,\,x < 0.~} \end{array}} \right.$(46)
${{C}_{{{{q}_{n}}}}} = {{\left( {2R\int\limits_0^{{{q}_{0}}} {{{J_{{{{q}_{n}}}}^{2}\left( y \right)dy} \mathord{\left/ {\vphantom {{J_{{{{q}_{n}}}}^{2}\left( y \right)dy} y}} \right. \kern-0em} y}} } \right)}^{{ - 0.5}}}.$(47)
${{C}_{q}} = {{\left( {\frac{{2R\Gamma \left( {2q + 1} \right)\surd \pi }}{{{{2}^{{2q{\kern 1pt} \, + \,{\kern 1pt} 1}}}q{{\Gamma }}\left( {q + 1} \right)\Gamma \left( {q + 0.5} \right)}}} \right)}^{{ - 0.5}}}.$(48)
$\begin{gathered} \left( {{{E}_{{{{q}_{m}}}}} - {{E}_{{{{q}_{n}}}}}} \right)\int {{{\psi }_{{{{q}_{n}}}}}\left( x \right)~{{\psi }_{{{{q}_{m}}}}}\left( x \right)dx} = \\ = \left( {\frac{{{{\hbar }^{2}}}}{{2m}}} \right)\left( {{{\psi }_{{{{q}_{m}}}}}\left( x \right)\psi _{{{{q}_{n}}}}^{*}\left( x \right) - \psi _{{{{q}_{n}}}}^{*}\left( x \right)\psi _{{{{q}_{m}}}}^{'}\left( x \right)} \right)\begin{array}{*{20}{c}} {x = 0 + \,\,} \\ {x = 0 - .} \end{array}~ \\ \end{gathered} $(49)
$\begin{gathered} {{Q}_{{{{p}_{x}}}}}\left( K \right) = \int\limits_{ - \infty }^\infty {{\text{exp}}\left( { - i{{p}_{x}}x} \right){{\psi }_{q}}\left( x \right)dx} = \\ = {{C}_{q}}\left[ {{{{\left( {\frac{{{{q}_{0}}}}{2}} \right)}}^{{ - i{{q}_{1}}}}}\frac{2}{{q - {{q}_{1}}}}\frac{{{{\Gamma }}\left( {\frac{{q + i{{q}_{1}}}}{2}} \right)}}{{{{\Gamma }}\left( {\frac{{q - i{{q}_{1}}}}{2}} \right)}}} \right. + \\ \left. { + \,\,{{{\left( {\frac{{{{q}_{0}}}}{2}} \right)}}^{{i{{q}_{1}}}}}\frac{2}{{q + {{q}_{1}}}}\frac{{{{\Gamma }}\left( {\frac{{q - i{{q}_{1}}}}{2}} \right)}}{{{{\Gamma }}\left( {\frac{{q + i{{q}_{1}}}}{2}} \right)}}} \right]. \\ \end{gathered} $(50)
$\begin{gathered} {{Q}_{{{{p}_{x}}}}}\left( K \right) = {{C}_{q}}\frac{1}{Z} \times \\ \times \,\,{\text{cos}}{\kern 1pt} \left[ {{{\varphi }_{1}} - C{{q}_{1}} + {\text{ln}}{\kern 1pt} \left( {{2 \mathord{\left/ {\vphantom {2 {{{q}_{0}}}}} \right. \kern-0em} {{{q}_{0}}}}} \right){{q}_{1}} + \sum\limits_{K{\kern 1pt} = {\kern 1pt} 1}^\infty {\left( { - {\kern 1pt} 2{{\varphi }_{K}} + {{{{q}_{1}}} \mathord{\left/ {\vphantom {{{{q}_{1}}} K}} \right. \kern-0em} K}} \right)} } \right]{\kern 1pt} , \\ \end{gathered} $(51)
$\begin{gathered} Z = \frac{{\sqrt {{{q}^{2}} + q_{1}^{2}} }}{2},\,\,\,\,{\text{tg}}{{\varphi }_{K}} = {{{{q}_{1}}} \mathord{\left/ {\vphantom {{{{q}_{1}}} {\left[ {q + 2\left( {K - 1} \right)} \right]}}} \right. \kern-0em} {\left[ {q + 2\left( {K - 1} \right)} \right]}}, \\ K = 1,2 \ldots \,\,. \\ \end{gathered} $(52)
$\begin{gathered} {{Q}_{{{{p}_{x}}}}}\left( K \right) = \frac{{4{{C}_{q}}}}{{\sqrt {{{q}^{2}} + q_{1}^{2}} }} \times \\ \times \,\,{\text{cos}}\left[ {{\text{arctg}}\left( {\frac{{{{q}_{1}}}}{{{{q}_{0}}}}} \right)q + {{q}_{1}}{\text{ln}}\left( {\frac{{\sqrt {{{q}^{2}} + q_{1}^{2}} }}{{l{{q}_{0}}}}} \right)} \right]. \\ \end{gathered} $(53)
${{Q}_{{{{q}_{1}}}}}\left( q \right) \approx \left( {{{4{{C}_{q}}} \mathord{\left/ {\vphantom {{4{{C}_{q}}} q}} \right. \kern-0em} q}} \right)\cos \left[ {{{q}_{1}}{\text{ln}}\left( {{q \mathord{\left/ {\vphantom {q {{{q}_{0}}}}} \right. \kern-0em} {{{q}_{0}}}}} \right)} \right].$В уравнении (53) виден эффект осцилляций заселенности уровней поперечного движения с вариацией поперечного импульса влета q1. Такой же эффект осцилляций, но менее очевидный, содержится и в более общих выражениях (50) и (52). Приведем теперь результаты аналитических расчетов матричных элементов квантовых переходов каналированных электронов Mq между подбарьерными уровнями поперечного движения, не прибегая к предположению о дипольности переходов, что особенно существенно при расчете эффектов генерации возбужденных каналированной частицей фотонов и электронов в кристалле, а также фононов в кристалле [16, 17]:
(54)
${{M}_{{{{q}_{n}}{{q}_{{n{\kern 1pt} '}}}}}} = \int\limits_{ - \infty }^{ + \infty } {{{\psi }_{{{{q}_{n}}}}}\left( x \right){\text{exp}}\left( { - {{q}_{x}}x} \right){{\psi }_{{{{q}_{{n{\kern 1pt} '}}}}}}\left( x \right)dx} .$(55)
$M_{{nn{\kern 1pt} '}}^{{ee}}\left( {{{q}_{x}}} \right) = K_{{nn{\kern 1pt} '}}^{{{\text{чч}}}}\left( {{{q}_{x}}} \right) + K_{{nn{\kern 1pt} '}}^{{{\text{чч}}}}\left( { - {{q}_{x}}} \right),$(56)
$M_{{nn{\kern 1pt} '}}^{{eodd}}\left( {{{q}_{x}}} \right) = K_{{nn{\kern 1pt} '}}^{{{\text{чч}}}}\left( {{{q}_{x}}} \right) - K_{{nn{\kern 1pt} '}}^{{{\text{чч}}}}\left( { - {{q}_{x}}} \right),$(57)
${{K}_{{nn{\kern 1pt} '}}}\left( {{{q}_{x}}} \right) = \int\limits_0^1 {dy{{y}^{{ - 2i{{q}_{x}}R{\kern 1pt} \, - \,{\kern 1pt} 1}}}{{J}_{{{{q}_{n}}}}}\left( {{{q}_{0}}y} \right){{J}_{{{{q}_{{n{\kern 1pt} '}}}}}}\left( {{{q}_{0}}y} \right).} $После разложения функции Jq (без ограничения общности полагаем q > q') в ряд по степеням аргумента интеграл в уравнении (57) берется для каждого члена ряда [18, 19], в результате имеем:
(58)
$\begin{gathered} {{K}_{{nn{\kern 1pt} '}}}\left( {{{q}_{x}}} \right) = \sum\limits_{m{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}{{{0.5}}^{{2m{\kern 1pt} \, + \,{\kern 1pt} q}}}}}{{m!{{\Gamma }}\left( {m + q + 1} \right)}}q_{0}^{{2i{{q}_{x}}R}} \times } \\ \times \,\,\left[ {\left( {q{\kern 1pt} '\, + 2i{{q}_{x}}R - 2 + 2m + q} \right){{q}_{c}}{{J}_{{q{\kern 1pt} '}}}\left( {{{q}_{0}}} \right){{ + }^{{^{{^{{}}}}}}}} \right. \\ + \,\,{{S}_{{ - 2i{{q}_{x}}R{\kern 1pt} \, - \,{\kern 1pt} 2{\kern 1pt} \, + \,{\kern 1pt} 2m{\kern 1pt} \, + \,{\kern 1pt} q,q{\kern 1pt} '\,{\kern 1pt} - \,{\kern 1pt} 1}}}\left( {{{q}_{c}}} \right) - \\ - \,\,{{q}_{c}}{{J}_{{q{\kern 1pt} '\,{\kern 1pt} - \,{\kern 1pt} 1}}}\left( {{{q}_{0}}} \right){{S}_{{2i{{q}_{x}}R{\kern 1pt} \, - \,{\kern 1pt} 2m{\kern 1pt} \, + \,{\kern 1pt} q,q{\kern 1pt} '}}}\left( {{{q}_{c}}} \right) + \\ + \,\,{{2}^{{ - 2i{{q}_{x}}R{\kern 1pt} - {\kern 1pt} 1{\kern 1pt} + {\kern 1pt} 2m{\kern 1pt} + {\kern 1pt} q}}}\left. {\frac{{{{\Gamma }}\left( {q + m - i{{q}_{x}}R} \right)}}{{{{\Gamma }}\left( {q - m - i{{q}_{x}}R} \right)}}} \right]. \\ \end{gathered} $(59)
$\begin{gathered} {{K}_{{nn{\kern 1pt} '}}}\left( {{{q}_{x}}} \right) = K_{{nn{\kern 1pt} '}}^{{\left( a \right)}}\left( {{{q}_{x}}} \right) + \\ + \,\,\sum\limits_{m{\kern 1pt} \, = {\kern 1pt} \,0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{m}}{{{0.5}}^{{2m\,{\kern 1pt} + \,{\kern 1pt} q}}}}}{{m!{{\Gamma }}\left( {m + q + 1} \right)}}q_{0}^{{2i{{q}_{x}}R}} \times } \\ \,\, \times \left[ {{{S}_{{ - 2i{{q}_{x}}R{\kern 1pt} \, - {\kern 1pt} \,2\,{\kern 1pt} + {\kern 1pt} \,2m\,{\kern 1pt} + \,{\kern 1pt} q,q{\kern 1pt} '{\kern 1pt} \, - {\kern 1pt} \,1}}}\left( {{{q}_{0}}} \right) - } \right. \\ \left. { - \,\,{{q}_{0}}{{J}_{{q{\kern 1pt} '{\kern 1pt} \, - {\kern 1pt} \,1}}}\left( {{{q}_{0}}} \right){{S}_{{ - 2i{{q}_{x}}R{\kern 1pt} \, - {\kern 1pt} \,1{\kern 1pt} \, + {\kern 1pt} \,2m{\kern 1pt} \, + \,{\kern 1pt} q,q{\kern 1pt} '}}}\left( {{{q}_{0}}} \right)} \right] + K_{{nn{\kern 1pt} '}}^{{\left( d \right)}}\left( {{{q}_{x}}} \right). \\ \end{gathered} $(60)
$K_{{nn{\kern 1pt} '}}^{{\left( a \right)}}\left( {{{q}_{x}}} \right) = q_{0}^{{2i{{q}_{x}}R{\kern 1pt} \, + \,{\kern 1pt} 1}}{{J}_{{q{\kern 1pt} '}}}\left( {{{q}_{0}}} \right)\left( {q{\kern 1pt} '\, - 2i{{q}_{x}}R - 2} \right){{J}_{q}}\left( {0.5} \right).$(61)
$\begin{gathered} K_{{nn{\kern 1pt} '}}^{{\left( d \right)}}\left( {{{q}_{x}}} \right) = \frac{{{{2}^{{ - 2i{{q}_{x}}R{\kern 1pt} \, - \,{\kern 1pt} 1}}}}}{\pi }\sin \left( {\frac{{q - q{\kern 1pt} '}}{2} + i{{q}_{x}}R} \right){{\Gamma }}\left( {i2{{q}_{x}}R + 1} \right) \times \\ \times \,\,\frac{{{{\Gamma }}\left( {\frac{{q - q{\kern 1pt} '}}{2} - i{{q}_{x}}R} \right)}}{{{{\Gamma }}\left( {\frac{{q - q{\kern 1pt} '}}{2} + i{{q}_{x}}R + 1} \right)}}\frac{{{{\Gamma }}\left( {\frac{{q + q{\kern 1pt} '}}{2} - i{{q}_{x}}R} \right)}}{{{{\Gamma }}\left( {\frac{{q + q{\kern 1pt} '}}{2} + i{{q}_{x}}R + 1} \right)}}. \\ \end{gathered} $В случае надбарьерных каналированных электронов в кристалле нельзя ограничиваться приближением изолированной плоскости, и потенциал кристаллографической плоскости запишем в виде:
(62)
$\begin{gathered} V\left( x \right) = - {{V}_{0}}{\text{exp}}\left( { - \frac{{\left| {x - 2na} \right|}}{{2R}}} \right), \\ a\left( {2n - 1} \right) < x < a\left( {2n + 1} \right),\,\,\,\,n = 0,\, \pm {\kern 1pt} 1,\, \pm {\kern 1pt} 2 \ldots \,. \\ \end{gathered} $Коэффициенты А, С, D в выражениях (63), (64) и зонный спектр блоховского каналированного электрона определяются из условий сшивки волновой функции (42), (43) в точке x = 0:
(66)
$\frac{{\partial {{\Psi }_{q}}}}{{\partial x}}(x = a) = \frac{{\partial {{\Psi }_{q}}}}{{\partial x}}(x = - a)\exp (i2{{q}_{x}}a).$(67)
$C = \frac{{ - J_{{iq}}^{{\text{'}}}({{q}_{0}})}}{{J_{{ - iq}}^{{\text{'}}}({{q}_{0}})}}\frac{{(A + 1)}}{2} + \frac{{{{J}_{{iq}}}({{q}_{0}})}}{{{{J}_{{ - iq}}}({{q}_{0}})}}\frac{{(A - 1)}}{2},$(68)
$D = \frac{{ - J_{{iq}}^{{\text{'}}}({{q}_{0}})}}{{J_{{ - iq}}^{{\text{'}}}({{q}_{0}})}}\frac{{(A + 1)}}{2} - \frac{{{{J}_{{iq}}}({{q}_{0}})}}{{{{J}_{{ - iq}}}({{q}_{0}})}}\frac{{(A - 1)}}{2},$(70)
$\begin{gathered} P = 1 + {{\left\{ {2{{{\left[ {\frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}} \right]}}^{2}} + 4\frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}\left[ {\frac{{J_{{iq}}^{{\text{'}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( \beta \right)}} + \frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}} \right] - 2\frac{{J_{{iq}}^{{\text{'}}}\left( \beta \right){{J}_{{iq}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( \beta \right){{J}_{{ - iq}}}\left( \beta \right)}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {2{{{\left[ {\frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}} \right]}}^{2}} + 4\frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}\left[ {\frac{{J_{{iq}}^{{\text{'}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( \beta \right)}} + \frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}} \right] - 2\frac{{J_{{iq}}^{{\text{'}}}\left( \beta \right){{J}_{{iq}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( \beta \right){{J}_{{ - iq}}}\left( \beta \right)}}} \right\}} {}}} \right. \kern-0em} {}} \\ \left\{ {{{{\left[ {\frac{{J_{{iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right)}}} \right]}}^{2}} - {{{\left[ {\frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{{{J}_{{ - iq}}}\left( {{{q}_{0}}} \right)}}} \right]}}^{2}} + 2\left[ {\frac{{J_{{iq}}^{{\text{'}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( \beta \right)}} + \frac{{{{J}_{{iq}}}\left( \beta \right)}}{{J{{ - }_{{iq}}}\left( \beta \right)}}} \right]\left[ {\frac{{J_{{iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right)}} - \frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{J{{ - }_{{iq}}}\left( {{{q}_{0}}} \right)}}} \right]} \right\}. \\ \end{gathered} $(71)
$\begin{gathered} A\left[ {2 - \frac{{J_{{iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right){{J}_{{ - iq}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right){{J}_{{iq}}}\left( \beta \right)}} - \frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right){{J}_{{ - iq}}}\left( \beta \right)}}{{{{J}_{{ - iq}}}\left( {{{q}_{0}}} \right){{J}_{{iq}}}\left( \beta \right)}}} \right] + \\ + \,\,\left[ {\frac{{J_{{iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right){{J}_{{ - iq}}}\left( \beta \right)}}{{J_{{ - iq}}^{{\text{'}}}\left( {{{q}_{0}}} \right){{J}_{{iq}}}\left( \beta \right)}} + \frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right){{J}_{{ - iq}}}\left( \beta \right)}}{{{{J}_{{ - iq}}}\left( {{{q}_{0}}} \right){{J}_{{iq}}}\left( \beta \right)}}} \right] = {\text{exp}}\left( {i{{q}_{x}}2a} \right). \\ \end{gathered} $(72)
$\frac{{{{J}_{{iq}}}\left( \beta \right)}}{{{{J}_{{ - iq}}}\left( \beta \right)}} \approx \frac{{1 + {\text{ch}}\left( {q\pi } \right){\text{sin}}\left( {2{{q}_{0}}} \right) - i{\text{cos}}\left( {2{{q}_{0}}} \right){\text{sh}}\left( {q\pi } \right)}}{{{\text{sin}}\left( {2{{q}_{0}}} \right) + {\text{ch}}\left( {q\pi } \right)}},$(73)
$\frac{{{{J}_{{iq}}}\left( {{{q}_{0}}} \right)}}{{{{J}_{{ - iq}}}\left( {{{q}_{0}}} \right)}} \approx \frac{{1 - {\text{ch}}\left( {q\pi } \right){\text{sin}}\left( {2{{q}_{0}}} \right) + i{\text{cos}}\left( {2{{q}_{0}}} \right){\text{sh}}\left( {q\pi } \right)}}{{ - {\text{sin}}\left( {2{{q}_{0}}} \right) + {\text{ch}}\left( {q\pi } \right)}}{\kern 1pt} .$(74)
${{J}_{{ \pm iq}}}\left( \beta \right) \approx {{{{{\left( {\frac{\beta }{2}} \right)}}^{{ \pm iq}}}} \mathord{\left/ {\vphantom {{{{{\left( {\frac{\beta }{2}} \right)}}^{{ \pm iq}}}} {\Gamma \left( {1 \pm iq} \right).}}} \right. \kern-0em} {\Gamma \left( {1 \pm iq} \right).}}$Формулы (63), (64), (71) описывают как надбарьерный, так и подбарьерный зонный спектр каналированного электрона. В соответствующих формулах мнимые индексы функций Бесселя следует заменить на действительные iq → q. Зонные волновые функции подбарьерного движения необходимо применять для описания состояний каналированного электрона вблизи границы дискретного и непрерывного спектров, где приближение изолированной кристаллографической плоскости (62) неоправданно. В случае подбарьерных зон дисперсионное уравнение (71) (после замены ±iq → ±q) позволяет вычислить и ширины соответствующих зон. Для определения верхней и нижней по энергии границы зоны необходимо решить уравнение (71) относительно q, подставляя вместо exp(iqx2a) “+1” и “–1” соответственно.
ИНТЕНСИВНОСТЬ ИНДУЦИРОВАННЫХ ТОКОВ В КРИСТАЛЛЕ
Вычислим спектрально-угловую плотность вероятности не дипольного излучения жестких фотонов высокоэнергетической каналированной частицей с энергией, удовлетворяющей неравенству U0E ≥ 1. Известно, что не дипольные процессы излучения жестких фотонов не могут быть описаны при этих значениях энергии в квазиклассическом приближении [16, 17, 20–25]. В случае неполяризованного излучения можно записать следующее выражение для такой плотности вероятности [20, 21]:
(75)
$\begin{gathered} \frac{{{{d}^{2}}w\left( {\omega ,\theta } \right)}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}\omega }}{{2\pi }} \times \\ \times \,\,\sum\limits_f {\left\{ {\left( {1 + u + \frac{{{{u}^{2}}}}{2}} \right)} \right.} \left[ {{{{\left| {I_{{if}}^{{\left( 1 \right)}}\left( {{{k}_{x}}} \right)} \right|}}^{2}}{{\theta }^{2}} + {{{\left| {I_{{if}}^{{\left( 2 \right)}}\left( {{{k}_{x}}} \right)} \right|}}^{2}} - } \right. \\ \left. { - \,\,2{\text{Re}}\left( {I_{{if}}^{{\left( 1 \right)}}\left( {{{k}_{x}}} \right)I_{{if}}^{{\left( 2 \right)*}}\left( {{{k}_{x}}} \right)} \right)\theta {\text{cos}}\varphi } \right] + \\ + \,\,\frac{{{{u}^{2}}}}{{2{{e}^{2}}}}\left. {{{{\left| {I_{{if}}^{{\left( 1 \right)}}\left( {{{k}_{x}}} \right)} \right|}}^{2}}} \right\} \times \\ \times \,\,\delta \left( {2\frac{\omega }{{E - \omega }}{\kern 1pt} {\kern 1pt} \left[ {({{\theta }^{2}} + {{E}^{{ - 2}}})E - \omega {{\theta }^{2}}{{{\cos }}^{2}}\varphi } \right] - } \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} - \,\,{{\varepsilon }_{i}}\left( E \right) + {{\varepsilon }_{f}}\left( {E - \omega } \right)} \right). \\ \end{gathered} $(76)
$\begin{gathered} \frac{{{{d}^{2}}{{w}_{{if}}}\left( {\theta ,\varphi } \right)}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}\omega }}{{2\pi }}\mathop \sum \limits_f \left( {1 + {{u}_{{if}}} + {{u_{{if}}^{2}} \mathord{\left/ {\vphantom {{u_{{if}}^{2}} 2}} \right. \kern-0em} 2}} \right) \times \\ \times \,\,\frac{{u_{{if}}^{2}}}{{2{{E}^{2}}}}{{\left| {I_{{if}}^{{\left( 1 \right)}}\left( 0 \right)} \right|}^{2}}\delta \left( {{{\varepsilon }_{i}}\left( E \right) - {{\varepsilon }_{f}}\left( {E - \omega } \right) - \frac{\omega }{{E - \omega }}\frac{2}{E}} \right). \\ \end{gathered} $(77)
$\begin{gathered} \frac{{d{{w}_{{if}}}\left( \theta \right)}}{{d\Omega }} = \int {d\omega \frac{{{{d}^{2}}{{w}_{{if}}}\left( \theta \right)}}{{d\omega d\Omega }}} = \\ = \frac{{{{e}^{2}}{{\omega }_{{if}}}}}{\pi }\frac{{u_{{if}}^{2}}}{{4{{E}^{2}}}}\left( {1 + {{u}_{{if}}} + {{u_{{if}}^{2}} \mathord{\left/ {\vphantom {{u_{{if}}^{2}} 2}} \right. \kern-0em} 2}} \right){{\left| {I_{{if}}^{{\left( 1 \right)}}\left( 0 \right)} \right|}^{2}}. \\ \end{gathered} $(78)
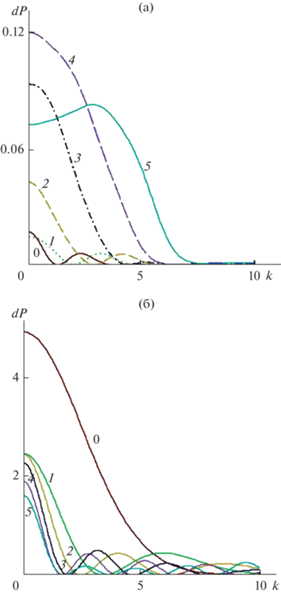
$\begin{gathered} {{w}_{{if}}}\left( {{{\omega }_{{if}}}} \right) = d{{w}_{{if}}}\left( {{{\omega }_{{if}}}} \right)d\Omega = \\ = \frac{{{{e}^{2}}}}{{hc\pi }}\frac{{\hbar {{\omega }_{{if}}}}}{\pi }\frac{{{{{\left( {\hbar {{\omega }_{{if}}}} \right)}}^{2}}}}{{{{{\left( {E - \hbar {{\omega }_{{if}}}} \right)}}^{2}}}}\frac{{{{{(m{{c}^{2}})}}^{2}}}}{{{{E}^{2}}}} \times \\ \times \,\,\left( {1 + {{u}_{{if}}} + \frac{{u_{{if}}^{2}}}{2}} \right){{\left| {I_{{if}}^{{\left( 1 \right)}}\left( {{{k}_{x}} \approx 0} \right)} \right|}^{2}}d{{\Omega }} = \\ = 2 \times {{10}^{{ - 3}}} \times 0.6 \times {{10}^{{25}}} \times {{0.66}^{2}} \times {{(4 \times {{10}^{4}})}^{{ - 2}}} \times \\ \times \,\,1.5 \times 5 \times 3.6 \times {{10}^{{ - 16}}} \times {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s} \approx 0.2{{s}^{{ - 1}}}. \\ \end{gathered} $Рис. 4.
Квадрат модуля dP не дипольных матричных элементов второго (а) и первого типа (б) для перехода позитрона с энергией, соответствующей q = 71, в состояние с энергией q = 51 между четными уровнями с изменением числа n нечетных (а) и четных (б) зон поперечной энергии, каналированной в зависимости от больших значений угла падения позитрона на кристалл. Угол θ измеряется как отношение поперечного импульса к продольному импульсу, выраженного в единицах, пропорциональных количеству векторов обратной решетки. Номера кривых соответствуют квантовым переходам позитрона с изменением номера зоны на данное число n, n = 0 отвечает квантовым переходам позитрона без изменения номера уровня поперечного движения.
Поскольку индуцированный ориентированной частицей квазифотомагнитный ток пропорционален интенсивности испускаемых фотонов, получаем весьма заметный квазифотомагнитный ток даже от одной каналированной частицы, испускающей фотоны в кристалле. При этом квазифотомагнитный ток ориентационно зависит от угла влета каналированной частицы в кристалл.
ВЫВОДЫ
Обсуждаемые в настоящей работе квазифотогальванический и квазифотомагнитный эффекты будут весьма удобным инструментом для изучения ориентационных явлений [7, 8, 16, 17, 20–28] при прохождении ориентированной частицы через кристалл, а также для изучения анизотропии электронно-фононного взаимодействия [29]. Из ориентационной зависимости многих эффектов, обусловленных эффектом каналирования, а также из ориентационной зависимости интенсивности испускаемых каналированной частицей жестких фотонов [16, 17, 20–28] следует ориентационная зависимость квазифотогальванического и квазифотомагнитного токов, которую легко можно будет наблюдать в эксперименте. Уравнения (1)–(4) в случае воздействия ультракороткого импульса ориентированной частицы на кристалл описывают динамический отклик электронно-фононной системы кристалла на такое воздействие [30], вполне аналогичный отклику кристалла на пикосекундные возбуждающие световые импульсы [31, 32]. В случае прохождения через кристалл ультракороткого (например, пикосекундного) пространственно-модулированного импульса ориентированной частицы в кристалле будут наблюдаться динамические решетки на неравновесных носителях заряда, аналогичные решеткам, индуцируемым в кристаллах полем двух когерентных интерферирующих электромагнитных волн [33].
Список литературы
Белиничер В.И., Стурман Б.И. // УФН. 1980. Т. 130. № 2. С. 415.
Белиничер В.И., Ивченко Е.Л., Стурман Б.И. // ЖЭТФ. 1982. Т. 83. №. 2. С. 649.
Гринберг А.А. // ЖЭТФ. 1970. Т. 58. №. 3. С. 989.
Kikoin I.K., Noskov M.M. // Phys. Z. Sowietunion. 1934. V. 5. P. 586.
Kikoin I.K. // Phys. Z Sowietunion, 1934. V. 6. P. 478.
Мазур Е.А. Возбуждение и релаксация полупроводника, генерация дефектов при воздействии импульсом быстрых ориентированных частиц // XII Совещ. по теории полупроводников. Киев: ИФП, 1985. Ч. 2. С. 93.
Мазур Е.А. // Кинетические явления в полупроводниках и диэлектриках. М.: Энергоатомиздат, 1985. С. 58.
Мазур Е.А. Ориентационные эффекты при возбуждении фононов и плазмонов каналированной частицей // XVI Всесоюзн. совещ. по физике взаимодействия заряженных частиц с кристаллами. М.: МГУ, 1986. С. 24.
Gemmel D.S. // Rev. Modern Phys. 1974. V. 46. P. 129.
Кубо Р. // Вопросы квантовой теории необратимых процессов / Ред. Бонч-Бруевич В.Л. М.: Изд-во иностр. лит., 1961. С.39.
Каган Ю.М., Кононец Ю.В. // ЖЭТФ. 1970. Т. 58. № 1. С. 226.
Каган Ю.М., Кононец Ю.В. // Теория эффекта каналирования. М.: МИФИ, 1976. С. 92.
Мазур Е.А. // Исследование поверхностных и объемных свойств твердых тел по взаимодействию частиц. М.: Энергоатомиздат, 1981. С. 381.
Мазур Е.А. Резонансные эффекты в рассеянии ориентированных пучков лептонов в кристаллах // Тр. XV Всесоюз. совещ. по взаимодействию быстрых заряженных частиц с кристаллами. М.: МГУ, 1986. С. 53.
Мазур Е.А. // Исследование поверхностных и объемных свойств твердых тел по взаимодействию частиц. М.: Энергоатомиздат, 1981. С. 65.
Калашников Н.П., Maзур E.A. // ЖЭТФ. 2019. Т. 155. № 4. С. 579.
Kalashnikov N.P., Mazur. E.A. // J. Surf. Invest.: X-ray, Synchrotron Neutron Tech. 2019. V. 13. № 6. P. 1135.
Справочник по специальным функциям / Ред. Абрамовиц М., Стиган И. М.: Наука, 1979. 832 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.
Базылев В.А., Жеваго Н.К. Излучение быстрых частиц в веществе и во внешних полях. М.: Наука, 1987. 272 с.
Жеваго Н.К. // ЖЭТФ. 1978. 75. С. 1389.
Барышевский В.Г. Каналирование, излучение и реакции в кристаллах при высоких энергиях. Mинск: Изд-во БГУ, 1982. 256 с.
Kumakhov M.A., Weddel R. Radiation of Relativistic Light Particles during Interaction with Single Crystals. Heidelberg: Spectrum, 1991. 322 c.
Ахиезер А.И., Шульга Н.Ф. Электродинамика частиц высоких энергий в веществе. M.: Наука, 1993. 344 с.
Akhiezer A.I., Shulga N.F. High-Energy Electrodynamics in Matter. Amsterdam: Gordon and Breach, 1996. 351 c.
Mazur E. // Nucl. Instrum. Methods Phys. Res. B. 2015. V. 355. P. 57.https://doi.org/10.1016/j.nimb.2015.02.013
Калашников Н.П., Maзур E.A., Ольчак А.С. // Ядерная физика. 2016. Т. 79. № 3. С. 390.
Kalashnikov N.P., Mazur E.A., Olczak A.S. // Int. J. Mod. Phys. A. 2015. V. 30. № 22. P. 1550137.
Мазур Е.А. // Письма в ЖЭТФ. 1986. Т. 43. № 8. С. 381.
Мазур Е.А. Пикосекундная лазерная спектроскопия импульсными пучками в полупроводниках // XII Всесоюз. конф. по когерентной и нелинейной оптике. М.: МГУ, 1985. Ч.П. С. 617.
Elci A., Scully J. // Phys. Rev. B. 1977. V. 16. № 1. P. 191.
Smirl A.J. // Phys. Rev. B. 1982. V. 25. № 4. P. 2645.
Винецкий В.Л., Кухтарев Н.В., Одулов С.Т., Соскин М.С. // УФН. 1979. Т. 129. № 1. С. 113.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования