1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 6, 2022

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 6, стр. 76-81

Влияние процессов многократного упругого рассеяния в многокомпонентных мишенях на интенсивность пиков упруго отраженных электронов

В. П. Афанасьев a, *, Л. Г. Лобанова a, **

a Национальный исследовательский университет “МЭИ”
111250 Москва, Россия

* E-mail: v.af@mail.ru
** E-mail: lida.lobanova.2017@mail.ru

Поступила в редакцию 18.07.2021
После доработки 24.09.2021
Принята к публикации 30.09.2021

Полный текст (PDF)

Аннотация

Представлено решение граничной задачи для описания процесса формирования пиков электронов, упруго отраженных от многокомпонентных образцов. Показано, что задача приводит к уравнениям типа Ляпунова и допускает построение эффективного численного решения. Построена малоугловая теория упругого отражения электронов от многокомпонентных материалов, что позволило получить аналитические решения, которые описывают интенсивность пиков электронов, отраженных от различных компонентов мишени. Создана методика интерпретации и количественной обработки пиков упруго отраженных электронов с учетом эффекта многократного рассеяния.

Ключевые слова: многокомпонентные мишени, спектроскопия упруго отраженных электронов, метод инвариантного погружения, малоугловое приближение.

ВВЕДЕНИЕ

Современная промышленно выпускаемая для задач электронной спектроскопии аппаратура позволяет определять пики электронов, квазиупруго отраженных (не попавших в неупругий канал рассеяния) от различных атомов многокомпонентного образца с энергетическим разрешением, удовлетворяющим критерию Рэлея [1]. Благодаря наличию установок с высоким энергетическим разрешением стало возможно определять элементный и изотопный состав исследуемой мишени начиная с водорода. Возможности новой разновидности электронной спектроскопии, названной спектроскопией упруго отраженных электронов (elastic peak electron spectroscopy), были ярко продемонстрированы в работах Maarten Vos [1–3], который назвал данную методику резерфордовским обратным рассеянием электронов. Спектроскопия упруго отраженных электронов [4] сняла с электронной спектроскопии запрет [5] на возможность фиксации в образцах изотопов водорода и гелия. С появлением новой разновидности спектроскопии возникла потребность создания методики обработки экспериментально измеренных спектров для получения количественной информации о послойном составе исследуемой мишени. Это приводит к необходимости решения ряда задач.

Первая – задача определения площади под пиком упруго отраженных электронов связана с вычитанием фона, созданного неупруго рассеянными электронами. Похожая проблема возникает и в рентгеновской фотоэлектронной спектроскопии [5]. Методы решения данной задачи представлены в [6–10].

Вторая – учет влияния многократного упругого рассеяния на уширение и смещение пика упруго отраженных электронов. В случае однократного упругого рассеяния электрона на ядре на угол θ происходит потеря энергии ΔE, следующая из законов сохранения энергии и импульса:

(1)
$\Delta E = {{2m} \mathord{\left/ {\vphantom {{2m} {M{{E}_{0}}}}} \right. \kern-0em} {M{{E}_{0}}}}\left( {1 - \cos \theta } \right) = {{4m} \mathord{\left/ {\vphantom {{4m} {M{{E}_{0}}}}} \right. \kern-0em} {M{{E}_{0}}}}{\text{si}}{{{\text{n}}}^{2}}{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. \kern-0em} 2},$
где m и M – массы электрона и ядра соответственно, E0 – энергия налетающего электрона. Из формулы (1) следует, что, например, при двукратном рассеянии на углы θ/2 электрон попадает в энергоанализатор с меньшей потерей энергии, чем при однократном рассеянии на угол θ. Таким образом, многократное упругое рассеяние приводит как к уширению, так и смещению пика в область меньших потерь энергии. Подробный анализ данного эффекта в однокомпонентных материалах представлен в [11].

Третья – последовательный учет влияния многократного упругого рассеяния на интенсивность пиков упруго отраженных электронов (упругих пиков) в многокомпонентных образцах представляет основу построения количественной методики.

Целью настоящей работы было определение границ применимости существующих аналитических теорий формирования пиков упруго отраженных электронов [12–14] к описанию многокомпонентных мишеней, построение аналитического метода расчета интенсивностей упругих пиков, сформированных каждым из компонентов мишени сложного состава.

АНАЛИЗ ТЕОРИЙ ФОРМИРОВАНИЯ ПИКОВ УПРУГО ОТРАЖЕННЫХ ЭЛЕКТРОНОВ

Выводить уравнение, описывающее упругое отражение электронов, будем с использованием метода инвариантного погружения Амбарцумяна [12–15]. Ограничимся случаем полубесконечной однородной среды, на поверхность которой (поверхность твердого тела, размер которого значительно превышает длину транспортного пробега электронов) добавим тонкий слой материала среды:

(2)
$dz \ll {{l}_{{{\text{el}}}}}$
и сформулируем условие неизменности функции отражения. Здесь lel – средняя длина свободного пробега электрона между упругими соударениями. Для функции упругого отражения от j-го компонента среды Rj(s, μ0, μ), которая определяет отношение числа электронов, отразившихся в единичный телесный угол, пройдя в мишени путь s, к потоку падающих частиц, запишем:
(3)
$\begin{gathered} \left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial s}}} \right. \kern-0em} {\partial s}} + 1} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}} + {1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0em} \mu }} \right){{R}_{j}}\left( {s,{{\mu }_{0}},\mu } \right) = \\ = {{\beta }_{j}}{{x}_{j}}\left( {{{\mu }_{0}},\mu } \right) + \int\limits_{ - 1}^0 {{{R}_{j}}} \left( {s,{{\mu }_{0}},\mu {\kern 1pt} {\text{'}}} \right)x\left( {\mu {\kern 1pt} {\text{'}},\mu } \right){{d\mu {\kern 1pt} {\text{'}}} \mathord{\left/ {\vphantom {{d\mu {\kern 1pt} {\text{'}}} {\mu {\kern 1pt} {\text{'}}}}} \right. \kern-0em} {\mu {\kern 1pt} {\text{'}}}} + \\ + \,\,\int\limits_0^1 {x\left( {{{\mu }_{0}},\mu {\kern 1pt} {\text{'}}} \right)} {{R}_{j}}\left( {s,\mu {\kern 1pt} {\text{'}},\mu } \right){{d\mu {\kern 1pt} {\text{'}}} \mathord{\left/ {\vphantom {{d\mu {\kern 1pt} {\text{'}}} {\mu {\kern 1pt} {\text{'}}}}} \right. \kern-0em} {\mu {\kern 1pt} {\text{'}}}}, \\ \end{gathered} $
(4)
${{\beta }_{j}} = \frac{{{{n}_{j}}{{\sigma }_{{{\text{el}}j}}}}}{{\sum\limits_k {\left( {{{n}_{k}}{{\sigma }_{{{\text{el}}k}}}} \right)} }},$
где nj – концентрация, μ0 и μ – косинусы углов падения и отражения соответственно (углы измеряются относительно нормали, проведенной вглубь слоя), x(μ) – индикатриса упругого рассеяния, равная отношению дифференциального сечения упругого рассеяния к полному сечению упругого рассеяния, ${{\sigma }_{{{\text{el}}j}}}$ – интегральное сечение упругого рассеяния на j-м компоненте, $\sum\nolimits_j {{{\beta }_{j}}} = 1.$

Подчеркнем, что формула (3) – это уравнение, описывающее чисто упругое рассеяние. Решение уравнения (3) будем искать на основе двух подходов: первый подход развит в [12], второй подход, или метод Освальда–Каспера–Гауклера (ОКГ), представлен в [13–15]. Наиболее важной особенностью уравнения (3) является отсутствие в нем нелинейного слагаемого, так как трехкратное рассеяние на большой угол приведет, в соответствии с формулой (1), к потере энергии, кратно превышающей ту, что соответствует положению j-го упругого пика электронов в энергетическом спектре. Таким образом, точное решение задачи определения интенсивности пика упруго отраженных электронов базируется на решении относительно простого, линейного интегрального уравнения. Отметим, что это не первая ситуация, когда метод инвариантного погружения приводит к линейному уравнению. Примером здесь является решение граничной задачи для уравнения Ландау [15, 16]. Упростить уравнение (3) удается благодаря “сильной вытянутости” сечения упругого рассеяния ωel(ψ):

(5)
${{\omega }_{{{\text{el}}}}}\left( 0 \right) \gg {{\omega }_{{{\text{el}}}}}\left( \pi \right).$
Наряду с уравнением (3) запишем уравнение, описывающее суммарную интенсивность пиков, упруго отраженных от всех компонентов соединения электронов:
(6)
${{R}^{m}}\left( {s,{{\mu }_{0}},\mu } \right) = \sum\limits_j {R_{j}^{m}\left( {s,{{\mu }_{0}},\mu } \right)} ,$
(7)
$\begin{gathered} \left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial s}}} \right. \kern-0em} {\partial s}} + 1} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}} + {1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0em} \mu }} \right)R\left( {s,{{\mu }_{0}},\mu } \right) = \\ = x({{\mu }_{0}},\mu ) + \int\limits_{ - 1}^0 {R(s,{{\mu }_{0}},\mu {\kern 1pt} ')x(\mu {\kern 1pt} ',\mu ){{d\mu {\kern 1pt} '} \mathord{\left/ {\vphantom {{d\mu {\kern 1pt} '} {\mu {\kern 1pt} '}}} \right. \kern-0em} {\mu {\kern 1pt} '}}} + \\ + \,\,\int\limits_0^1 {x({{\mu }_{0}},\mu {\kern 1pt} ')R(s,\mu {\kern 1pt} ',\mu )} {{d\mu {\kern 1pt} '} \mathord{\left/ {\vphantom {{d\mu {\kern 1pt} '} {\mu {\kern 1pt} '}}} \right. \kern-0em} {\mu {\kern 1pt} '}}. \\ \end{gathered} $
Уравнение (7) имеет вид, аналогичный уравнению отражения от однокомпонентных однородных образцов. Для решения (7) можно использовать метод ОКГ. Применение первого подхода позволяет найти решения как уравнения (3), так и уравнения (7). Но с помощью второго подхода, метода ОКГ, можно решить только уравнение (7). В [9] показано, что подход ОКГ для расчета относительных интенсивностей пиков упруго отраженных электронов от многокомпонентных мишеней приводит к результатам, не соответствующим экспериментальным данным.

Для реализации подхода ОКГ необходимо, чтобы сечения x(μ) в первом слагаемом правой части и сечения x(μ) во втором и третьем интегральных слагаемых были одинаковы. Указанное условие выполняется только для уравнения (7). Подход [12], позволяющий найти как решение уравнения (3), так и уравнения (7), дает значительную погрешность. Более точное ОКГ-решение позволит найти возможность кардинально уменьшить погрешность подхода [12]. Решение уравнения (7) на основе подхода [12] имеет вид:

(8)
$\begin{gathered} {{R}_{1}}\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}\sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right) \times \\ \times \,\,\left[ {({{x}^{l}} - 1){\kern 1pt} {\text{exp}}~\left( { - {\kern 1pt} (1 - {{x}^{l}}){s \mathord{\left/ {\vphantom {s \alpha }} \right. \kern-0em} \alpha }} \right) + {\text{exp}}~\left( {{{ - s} \mathord{\left/ {\vphantom {{ - s} \alpha }} \right. \kern-0em} \alpha }} \right)} \right], \\ \end{gathered} $
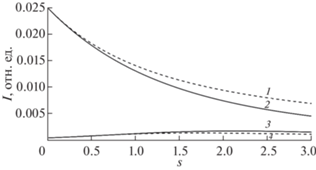
где ${{\mu }_{0}} \to \mu = {{\mu }_{0}}\mu + {{(1 - \mu _{0}^{2})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{(1 - {{\mu }^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ xl – коэффициенты разложения индикатрисы упругого рассеяния в ряд по полиномам Лежандра. Решение того же уравнения методом ОКГ, практически точно описывающее распределение частиц по длине пробега, имеет вид:
(9)
$\begin{gathered} {{R}_{2}}\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}\sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right) \times \\ \times \,\,\left[ {{\text{exp}}\,~\left( { - {\kern 1pt} (1 - {{x}^{l}})s} \right) + {\text{exp}}\left( { - s} \right)} \right].~ \\ \end{gathered} $
Последовательное решение уравнения (7) на основе метода [12] соответствует α = 1 в формуле (8). Вариация подгоночного параметра α позволит добиться наиболее адекватного совпадения расчетов на основе (8) с расчетами на основе (9). Указанное совпадение наблюдается при α = 2. Важно, что параметр α не зависит от геометрии, энергии и сорта атома, на котором происходит рассеяние.

Из рис. 1 видно, что наиболее качественно распределение частиц по длине пробега описывается функцией R1 в случае пробегов от нулевого до транспортного, что позволяет уверенно использовать формулу (8) для расчета интенсивностей упруго отраженных электронов, пробеги которых в мишени составляют величину lin, так как lin$ \ll $ ltr. Решение уравнений (3) и (7) легко найти в приближении прямолинейных траекторий (straight line approximation – SLA), когда индикатриса упругого рассеяния заменяется дельта-функцией:

(10)
${{x}_{j}}\left( {\mu ,\mu {\kern 1pt} {\text{'}}} \right) = \delta \left( {\mu - \mu {\kern 1pt} {\text{'}}} \right),$
(11)
$\begin{gathered} {{R}_{{{\text{SLA}}}}}\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}\sum\limits_j {{{\beta }_{j}}{{x}_{j}}\left( {{{\mu }_{0}},\mu } \right)} = \\ = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}x\left( {{{\mu }_{0}},\mu } \right). \\ \end{gathered} $
Метод, представленный в [12], и приближение прямолинейных траекторий позволяют найти функцию распределения частиц по длине пробега (path length distribution function) для потоков электронов, отраженных от каждого из компонентов мишени, или найти решение уравнения (3):
(12)
$\begin{gathered} {{R}_{{{{1}_{j}}}}}\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}\sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right) \times \\ \times \,\,{{\beta }_{j}}\left[ {(x_{j}^{l} - 1){\kern 1pt} {\text{exp}}~\left( { - {\kern 1pt} (1 - {{x}^{l}}){s \mathord{\left/ {\vphantom {s \alpha }} \right. \kern-0em} \alpha }} \right) + {\text{exp}}~\left( {{{ - s} \mathord{\left/ {\vphantom {{ - s} \alpha }} \right. \kern-0em} \alpha }} \right)} \right]~ \\ \end{gathered} $
и

(13)
${{R}_{{{\text{SL}}{{{\text{A}}}_{j}}}}}\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}{{\beta }_{j}}{{x}_{j}}\left( {{{\mu }_{0}},\mu } \right).$
Рис. 1.

Функции распределения частиц по длине пробега, вычисленные для Au (1, 2) и С (3, 4) в модифицированном малоугловом приближении по формуле (8) (2, 3) и на основе метода ОКГ по формуле (9) (1, 4). Угол падения 0°, угол отражения 145°, энергия зондирующих электронов 5 кэВ.

МЕТОДИКА ОПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТЕЙ ПИКОВ УПРУГО ОТРАЖЕННЫХ ЭЛЕКТРОНОВ

Упругие пики формируются вследствие движения в мишени электронов, не испытавших неупругих соударений. Вероятность испытать упругое соударение на отрезке l определяет закон Бугера exp(–l/lin), тогда угловое распределение интенсивности упруго отраженных электронов описывает формула:

(14)
$\begin{gathered} R\left( {{{\mu }_{0}},\mu } \right) = \int\limits_0^\infty {dl} {\kern 1pt} {\text{exp}}\left( {{{ - l} \mathord{\left/ {\vphantom {{ - l} {{{l}_{{{\text{in}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{in}}}}}}}} \right)R\left( {{l \mathord{\left/ {\vphantom {l {{{l}_{{{\text{el}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{el}}}}}}},{{\mu }_{0}},\mu } \right) = \\ = \int\limits_0^\infty {ds} {\kern 1pt} {\text{exp}}\left( { - s\frac{{1 - \lambda }}{\lambda }} \right)R\left( {s,{{\mu }_{0}},\mu } \right). \\ \end{gathered} $
Включение в рассмотрение процессов неупругого рассеяния делает необходимым определить альбедо для однократного рассеяния:
(15)
$\lambda = \frac{{\sum\limits_k {{{n}_{k}}{{\sigma }_{{{\text{el}}k}}}} }}{{\sum\limits_k {{{n}_{k}}{{\sigma }_{{{\text{el}}k}}}} + {{\sigma }_{{{\text{in}}}}}\sum\limits_k {{{n}_{k}}} }},$
где λ – вероятность того, что процесс однократного рассеяния произойдет упруго, ${{\sigma }_{{{\text{in}}}}}\sum\nolimits_k {{{n}_{k}}} = {1 \mathord{\left/ {\vphantom {1 {{{l}_{{{\text{in}}}}},}}} \right. \kern-0em} {{{l}_{{{\text{in}}}}},}}$ σin – интегральное сечение неупругого рассеяния, lin – длина свободного пробега при неупругом рассеянии:
(16)
${{\beta }_{j}}\lambda = {{\lambda }_{j}}.$
Подстановка формулы (13) в формулу (14) позволяет найти функцию распределения частиц по длине пробега в приближении прямолинейных траекторий:
(17)
${{R}_{{{\text{SL}}{{{\text{A}}}_{j}}}}}\left( {{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}\frac{{{{\beta }_{j}}\lambda {{x}_{j}}\left( {{{\mu }_{0}},\mu } \right)}}{{1 - \lambda }}.$
Подстановка формулы (12) в формулу (14) дает возможность найти ту же функцию в малоугловом приближении:
(18)
$\begin{gathered} {{R}_{{{{1}_{j}}}}}\left( {{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}{{\beta }_{j}}\lambda \alpha \sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right) \times \\ \times \,\,\frac{{x_{j}^{l}\left[ {\lambda + \alpha \left( {1 - \lambda } \right)} \right] - {{x}^{l}}\lambda }}{{\left[ {(1 - {{x}^{l}})\lambda + \alpha \left( {1 - \lambda } \right)} \right]\left[ {\lambda + \alpha \left( {1 - \lambda } \right)} \right]}}. \\ \end{gathered} $
Подстановка формулы (9) в формулу (14) дает угловое распределение электронов, отраженных от всех компонентов мишени:
(19)
$\begin{gathered} {{R}_{2}}\left( {{{\mu }_{0}},\mu } \right) = - \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }} \times \\ \times \,\,\sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right){\text{ln(}}1 - \lambda {{x}^{l}}{\text{)}}{\kern 1pt} . \\ \end{gathered} $
Аналогичная (18) формула для модифицированного малоуглового приближения, справедливая для однокомпонентной мишени либо описывающая суммарную площадь под всеми упругими пиками, имеет вид:
(20)
$\begin{gathered} {{R}_{1}}\left( {{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}\lambda {{\alpha }^{2}}\sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right) \times \\ \times \,\,\frac{{{{x}^{l}}\left( {1 - \lambda } \right)}}{{\left[ {(1 - {{x}^{l}})\lambda + \alpha \left( {1 - \lambda } \right)} \right]\left[ {\lambda + \alpha \left( {1 - \lambda } \right)} \right]}}. \\ \end{gathered} $
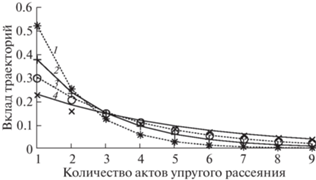
Еще раз отметим, что подход ОКГ позволяет найти лишь суммарную интенсивность всех пиков упруго отраженных частиц. Подход ОКГ позволяет разделить вклады в суммарный сигнал по кратности упругого рассеяния:
(21)
$\begin{gathered} {{R}_{2}}\left( {{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\mu }}{{{{\mu }_{0}} + \mu }}\sum\limits_{l{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {{{\mu }_{0}} \to \mu } \right) \times \\ \times \,\,\left[ {\lambda {{x}^{l}} + {{{{{({{\lambda }}{{x}^{l}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{({{\lambda }}{{x}^{l}})}}^{2}}} 2}} \right. \kern-0em} 2} + {{{{{(\lambda {{x}^{l}})}}^{3}}} \mathord{\left/ {\vphantom {{{{{(\lambda {{x}^{l}})}}^{3}}} 3}} \right. \kern-0em} 3} + \cdots + {{{{{(\lambda {{x}^{l}})}}^{k}}} \mathord{\left/ {\vphantom {{{{{(\lambda {{x}^{l}})}}^{k}}} k}} \right. \kern-0em} k} + ...} \right]. \\ \end{gathered} $
Каждое из слагаемых в квадратных скобках в формуле (21) определяет вклад однократного (первое слагаемое), двукратного (второе слагаемое), …, k-кратного упругого рассеяния в интенсивность пиков упруго отраженных электронов.

Рисунок 2 показывает определяющий вклад в интенсивность пиков упруго отраженных электронов процессов многократного упругого рассеяния. Наиболее существенен этот вклад в случае HfO2, поскольку для оксида гафния альбедо для однократного рассеяния λ = 0.8, и рассеяние можно считать близким к консервативному. С уменьшением альбедо вклад процессов многократного упругого рассеяния резко убывает, что наиболее заметно на рис. 2 в случае карбоната лития Li2CO3, для которого λ = 0.48, однако и в этом случае вклад кратных актов упругого рассеяния в интенсивность пика будет заметно превосходить вклад однократного рассеяния.

Рис. 2.

Суммарная интенсивность электронов, упруго отраженных от всех компонентов соединений Li2CO3, CaCO3, TiO2, HfO2, являющаяся результатом однократного, двукратного и так далее процессов упругого рассеяния и рассчитанная на основе формулы (21) для: Li2CO3 (1); CaCO3 (2); TiO2 (3); HfO2 (4). Символами обозначены результаты расчета методом Монте-Карло [16]. Угол падения 0°, угол отражения 135°, энергия зондирующих электронов 40 кэВ.

Рисунки 3 и 4 показывают хорошее совпадение результатов расчетов, выполненных в рамках модифицированной малоугловой теории (формула (20)) и метода ОКГ (формула (19)). Так как в [14, 15, 17] была продемонстрирована высокая точность метода ОКГ, представленные на рис. 3, 4 результаты позволяют утверждать, что описание интенсивностей пиков, упруго отраженных от компонентов соединения электронов на основе формулы (18) даст верные результаты.

Рис. 3.

Угловые распределения электронов, упруго отраженных от гафния, вычисленные в модифицированном малоугловом приближении (1), на основе метода ОКГ (2) и в приближении прямолинейных траекторий (3). Угол падения 0°, энергия зондирующих электронов 40 кэВ.

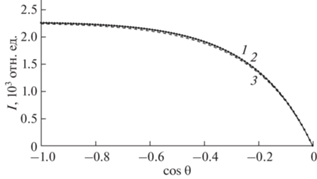
Рис. 4.

Угловые распределения электронов, упруго отраженных от гафния, вычисленные в модифицированном малоугловом приближении (1), на основе метода ОКГ (2) и в приближении прямолинейных траекторий (3). Угол падения 75°, энергия зондирующих электронов 40 кэВ.

Данные о составе многокомпонентных мишеней на основе спектроскопии упруго отраженных электронов получают, анализируя отношение интенсивностей пиков, измеренных в различной геометрии и при различной энергии зондирующего пучка. Рисунки 5, 6 позволяют оценить ошибку, допускаемую при определении компонентного состава мишени в рамках простейшей модели прямолинейных траекторий. Все расчеты, представленные в работе, получены на основе сечений и функции распределения частиц по длине пробега [18–22].

Рис. 5.

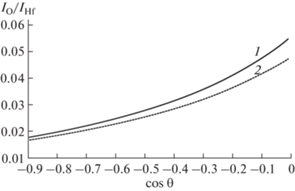
Угловые распределения электронов, упруго отраженных от гафния и кислорода (отношение интенсивностей пиков кислорода и гафния на основе формул (12) и (13)), вычисленные в модифицированном малоугловом приближении (1) и в приближении прямолинейных траекторий (2). Угол падения 0°, энергия зондирующих электронов 40 кэВ.

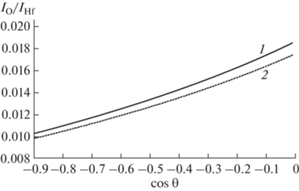
Рис. 6.

Угловые распределения электронов, упруго отраженных от гафния и кислорода (отношение интенсивностей пиков кислорода и гафния на основе формул (12) и (13)), вычисленные в модифицированном малоугловом приближении (1) и в приближении прямолинейных траекторий (2). Угол падения 75°, энергия зондирующих электронов 40 кэВ.

ЗАКЛЮЧЕНИЕ

Решена граничная задача описания процесса формирования пиков упруго отраженных электронов в энергетическом спектре. Показано, что в данной ситуации метод инвариантного погружения приводит к уравнениям, в которых отсутствует нелинейное слагаемое. Решение полученных уравнений построено на основе методики ОКГ [9, 10], модифицированного малоуглового приближения, приближения прямолинейных траекторий до и после упругого отражения на заданный угол.

В [14, 15] показана высокая точность описания процесса на основе метода ОКГ, и в настоящей работе этот подход являлся эталоном. Недостаток метода ОКГ состоит в невозможности раздельного описания интенсивностей пиков электронов, отраженных от различных компонентов мишени. Модифицированное малоугловое приближение (формулы (18) и (20)), практически с той же точностью описывающее процесс, что и метод ОКГ, дает возможность раздельно определить интенсивности пиков, сформированных в процессе отражения электронов от различных компонентов мишени.

В работе показана удовлетворительная точность описания сигналов в спектрах упруго отраженных электронов в рамках модели прямолинейных траекторий (формулы (11) и (13)). Простая модель формирования рентгеновских фотоэлектронных спектров сыграла очень важную роль в создании различных методик [5]. Учесть эффект многократного рассеяния в рентгеновской фотоэлектронной спектроскопии можно, вводя корректирующие поправки в простые формулы приближения прямолинейных траекторий [5]. Рисунки 5 и 6 показывают, что погрешность описания сигнала в спектрах упруго отраженных электронов для актуальных углов визирования пиков не превышает 10%.

Список литературы

  1. Went M.R., Vos M. // Surf. Interface Anal. 2007. V. 39. № 11. P. 871. https://doi.org/10.1002/sia.2603

  2. Vos M., Aizel K., Winkelmann A. // Surface Sci. 2010. V. 604. № 11. P. 893. https://doi.org/10.1016/j.susc.2010.02.016

  3. Vos M., Cornish G.P., Weigold E. // Rev. Sci. Instrum. 2000. V. 71. № 10. P. 3831. https://doi.org/10.1063/1.1290507

  4. Vos M. // Ultramicroscopy. 2002. V. 92. № 3–4. P. 143. https://doi.org/10.1016/S0304-3991(02)00127

  5. Hofmann S. Auger- and X-Ray Photoelectron Spectroscopy in Materials Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013. 505 p.

  6. Afanas’ev V.P., Gryazev A.S., Efremenko D.S., Kaplya P.S., Ridzel O.Yu. // J. Phys.: Conf. Ser. 2016. V. 748. № 1. P. 012005 https://doi.org/10.1088/1742-6596/748/1/012005

  7. Afanas’ev V.P., Gryazev A.S., Kaplya P.S., Köppen M., Ridzel O.Yu., Subbotin N.Yu., Hansen P. // J. Phys. Conf. Ser. 2017. V. 891. № 1. P. 012303 https://doi.org/10.1088/1742-6596/891/1/012303

  8. Афанасьев В.П., Грязев А.С., Капля П.С., Köppen M., Рыбакова А.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2019. № 9. С. 44. https://doi.org/10.1134/S0207352819090026

  9. Afanas’ev V.P., Kaplya P.S., Lobanova L.G. // J. Phys.: Conf. Ser. 2020. V. 1683. № 3. P. 032004 https://doi.org/10.1088/1742-6596/1683/3/032004

  10. Афанасьев В.П., Будак В.П., Ефременко Д.С., Капля П.С. // Светотехника. 2018. № 5. С. 44.

  11. Afanas’ev V.P., Afanas’ev M.V., Lubenchenko A.V., Batrakov A.A., Efremenko D.S., Vos M. // J. Electron Spectr. Related Phenomena. 2010. V. 177. № 1. P. 35. https://doi.org/10.1016/j.elspec.2010.01.002

  12. Afanas’ev V.P., Naujoks D. // Z. Phys. B. 1991. B. 84. № 3. S. 397. https://doi.org/10.1007/BF01314014

  13. Oswald R., Kasper E., Gaukler K. // J. Electron Spectr. Related Phenomena. 1993. V. 61. № 3. P. 251. https://doi.org/10.1016/0368-2048(93)80019-i

  14. Afanas’ev V.P., Kaplya P.S., Lisitsyna E.D. // J. Surf. Invest.: X-ray, Synchrotron Neutron Tech. 2016. V. 10. № 2. P. 326. https://doi.org/10.1134/S1027451016010043

  15. Afanas’ev V.P., Efremenko D.S., Kaplya P.S. // J. Electron Spectr. Related Phenomena. 2016. V. 210. P. 16. https://doi.org/10.1016/j.elspec.2016.04.006

  16. Landau L.D. // J. Phys. 1944. V. 8. P. 201.

  17. Afanas’ev V.P., Yagova N.V. // Z. Phys. B. 1993. B. 92. № 2. S. 199. https://doi.org/10.1007/BF01312178

  18. Vos M., Marmitt G.G., Grande P.L. // Surf. Interface Anal. 2016. V. 48. № 7. P. 415.https://doi.org/10.1002/sia.5948

  19. Salvat-Pujol F., Werner W. // Phys. Rev. B. 2011. V. 83. № 19. https://doi.org/10.1103/PhysRevB.83.195416

  20. NIST Electron Elastic-Scattering Cross-Section Database (2010) National Institute of Standards and Technology, Gaithersburg. https://srdata.nist.gov/srd64

  21. Dirac Partial-Wave Calculation of Elastic Scattering of Electrons and Positrons by Atoms, Positive Ions and Molecules. 2005. http://cpc.cs.qub.ac.uk/cpc/summaries/ADUS

  22. Tanuma S., Powell J., Penn D.R. // Surf. Interface Anal. 2005. V. 37. № 1. P. 1. https://doi.org/10.1002/sia.1997

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал