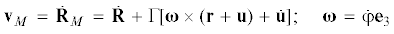Прикладная математика и механика, 2019, T. 83, № 1, стр. 32-38

СПИН-ОРБИТАЛЬНОЕ РЕЗОНАНСНОЕ ДВИЖЕНИЕ СПУТНИКА С ГИБКИМИ ВЯЗКОУПРУГИМИ СТЕРЖНЯМИ НА ЭЛЛИПТИЧЕСКОЙ ОРБИТЕ

Е. В. Садовникова^*, А. В. Шатина^**

Московский технологический университет (МИРЭА)
Москва, Россия

^* E-mail: sadovnikova-e@mail.ru
^** E-mail: shatina_av@mail.ru

Поступила в редакцию 11.07.2017

DOI: 10.1134/S0032823519010119

Аннотация

Изучается плоское вращательное движение спутника в центральном ньютоновском поле сил на эллиптической орбите. Спутник моделируется динамически симметричным твердым телом с жестко прикрепленными по оси симметрии гибкими вязкоупругими стержнями. При отсутствии деформаций в стержнях центральный эллипсоид инерции спутника представляет собой сферу. Получена усредненная система уравнений возмущенного движения вблизи резонанса 1:1 при малых значениях эксцентриситетов. Обоснован захват в спин-орбитальный резонанс 1:1.

Ключевые слова: спутник с гибкими вязкоупругими стрежнями, спин-орбитальный резонанс

Как известно, большинство крупных естественных спутников планет Солнечной системы вращаются синхронно: угловая скорость собственного вращения совпадает со средней скоростью движения по орбите (тогда спутник обращен к планете одной стороной). Однако синхронное вращение сферически симметричного спутника на эллиптической орбите неустойчиво и ведет к ускорению его вращения [1]. Наблюдаемое синхронное вращение спутников планет можно объяснить тем, что большинство из них имеют постоянные квадрупольные моменты, т.е. постоянные горбы (отклонения от сферичности).

Для изучения спин-орбитального взаимодействия рассмотрим модель спутника в виде твердого осесимметричного тела с жестко прикрепленными по оси симметрии вязкоупругими стержнями. Предполагается, что при отсутствии деформаций в стержнях главные центральные моменты инерции спутника равны между собой, т.е. его центральный эллипсоид инерции – сфера. Такая модель учитывает и отклонения от сферичности, и диссипативный аспект.

Ранее [2] рассматривалась неограниченная постановка задачи о поступательно-вращательном движении описанной модели спутника в центральном ньютоновском поле сил. Было показано, что в стационарном движении центр масс спутника движется по круговой орбите, а спутник неподвижен в орбитальной системе координат, т.е. его собственная угловая скорость совпадает с орбитальной. Переход к плоской ограниченной постановке задаче в данной работе обусловлен малостью линейных размеров спутника по сравнению с характерным размером орбиты [3]. Кроме того, эффект стремления эллиптических орбит к круговым за счет внутренней диссипации на много порядков слабее эффекта стабилизации спутников в окрестности плоских вращений вокруг нормали к плоскости орбиты [4, 5].

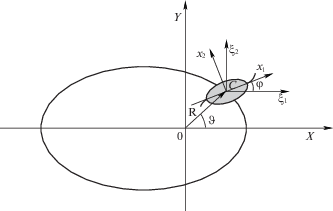
1. Постановка задачи. Уравнения движения. Пусть спутник, представляющий собой симметричное твердое тело, вдоль оси симметрии которого расположены два гибких вязкоупругих стержня, движется в центральном ньютоновском гравитационном поле на эллиптической орбите. Введем инерциальную систему координат $OXYZ$ с началом в притягивающем центре, совпадающем с одним из фокусов эллипса. Ось $OX$ направим по радиус-вектору перигея. Для описания вращательного движения спутника введем подвижную систему координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$, жестко связанную со спутником, и систему осей Кёнига $C{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$. Точка $C$ − центр масс спутника при отсутствии деформации стержней, когда стержни прямолинейны и расположены вдоль оси $C{{x}_{1}}$. Предполагается, что центр масс спутника $C$ движется по эллиптической орбите в плоскости $OXY$, ось $C{{x}_{3}}$ перпендикулярна плоскости орбиты, точки стержней перемещаются в плоскости $C{{x}_{1}}{{x}_{2}}$, совпадающей с плоскостью орбиты (фиг. 1).

Фиг. 1

Радиус-вектор точки стержня в системе координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$, согласно линейной теории изгиба тонких нерастяжимых стержней, имеет вид [2, 4]

(1.1)

$\begin{gathered} {{{\mathbf{r}}}_{{{\text{rod}}}}} = {\mathbf{r}} + {\mathbf{u}} \\ {\mathbf{u}} = u(s,t){{{\mathbf{e}}}_{2}},\quad {\mathbf{r}} = s{{{\mathbf{e}}}_{1}};\quad s \in K = [ - b - d \leqslant s \leqslant - b] \cup [b \leqslant s \leqslant b + d], \\ \end{gathered} $

где $u(s,t)$ − отклонение сечения стержня с координатой $s$ при изгибе, ${{{\mathbf{e}}}_{i}}$ − орт оси $C{{x}_{i}}$ ($i = 1,2,3$).

Обозначим через ${\mathbf{R}}$ радиус-вектор точки $C$. В системе координат $OXYZ{\text{:}}$

(1.2)

${\mathbf{R}} = R{{{\mathbf{e}}}_{R}},\quad R = \frac{{aq}}{p},\quad {{{\mathbf{e}}}_{R}} = (\cos \vartheta ,\sin \vartheta ,0)$

(1.3)

$\begin{gathered} \dot {\vartheta } = \frac{{\partial \vartheta }}{{\partial l}}\dot {l} = \sigma n,\quad q = 1 - {{e}^{2}},\quad p = 1 + e\cos \vartheta , \\ \sigma = \frac{{{{p}^{2}}}}{{{{q}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}},\quad n = \sqrt {\frac{\gamma }{{{{a}^{3}}}}} ,\quad l = n(t - {{t}_{0}}),\quad \gamma = G{{M}_{0}}, \\ \end{gathered} $

где $\vartheta $ − истинная аномалия, $a$ − большая полуось орбиты точки $C$, $e$ − эксцентриситет орбиты, $n$ − среднее движение центра масс $C$ по орбите, $l$ − средняя аномалия, $\,\,G$ − универсальная гравитационная постоянная, ${{M}_{0}}$ − масса притягивающего центра, ${{t}_{0}}$ − начальный момент времени. Величины $a$, $e$, $n$ − постоянные, точкой сверху обозначена производная по времени $t$.

Пусть $V$ − область в ${{{\rm E}}^{3}}$, занимаемая твердым телом и двумя недеформированными стержнями. Радиус-вектор точки M спутника в системе координат $OXYZ$ имеет вид

${{{\mathbf{R}}}_{M}} = {\mathbf{R}} + \Gamma ({\mathbf{r}} + {\mathbf{u}}),$

где ${\mathbf{r}} \in V$, ${\mathbf{u}} \equiv 0$ для точек твердого тела, $\Gamma $ − оператор перехода от подвижной системы координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе осей Кёнига $C{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$. Обозначим через $\varphi $ угол между осями $C{{\xi }_{1}}$ и $C{{x}_{1}}$. Тогда

(1.4)

$\Gamma = \Gamma \left( \varphi \right) = \left( {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \sin \varphi }&0 \\ {\sin \varphi }&{\cos \varphi }&0 \\ 0&0&1 \end{array}} \right)$

Скорость точки $M$ спутника определяется равенством

(1.5)

Кинетическая энергия спутника представляется функционалом

(1.6)

$\begin{gathered} T = \frac{1}{2}\int\limits_V {{\mathbf{v}}_{M}^{2}d\mu } = \frac{1}{2}m{{{{\mathbf{\dot {R}}}}}^{2}} + \frac{1}{2}\int\limits_V {{{{[{\mathbf{\omega }} \times ({\mathbf{r}} + {\mathbf{u}})]}}^{2}}d\mu } + \frac{1}{2}\int\limits_K {{{{{\mathbf{\dot {u}}}}}^{2}}\rho ds} + \\ + \;\int\limits_K {[{{\Gamma }^{{ - 1}}}{\mathbf{\dot {R}}},{\mathbf{\omega }} \times {\mathbf{u}} + {\mathbf{\dot {u}}}]\rho ds} + \int\limits_K {({\mathbf{\omega }} \times ({\mathbf{r}} + {\mathbf{u}}),{\mathbf{\dot {u}}})\rho ds} \\ \end{gathered} $

Здесь $\mu $ − мера на области $V,m$ − масса спутника, $\rho $ − линейная плотность стержней, которую считаем постоянной. Учтено равенство (1.5).

Потенциальная энергия гравитационного поля имеет вид

(1.7)

$\Pi = - \gamma \int\limits_V {\frac{{d\mu }}{{\sqrt {{{{[{\mathbf{R}} + \Gamma ({\mathbf{r}} + {\mathbf{u}})]}}^{2}}} }}} $

Введем обозначение для орта вектора ${\mathbf{R}}$, задаваемого в подвижной системе координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$:

(1.8)

${\mathbf{\xi }} = {{\Gamma }^{{ - 1}}}{\mathbf{R}}{\text{/}}R = ({{\xi }_{1}},{{\xi }_{2}},0),\quad {{\xi }_{1}} = \cos (\vartheta - \varphi ),\quad {{\xi }_{2}} = \sin (\vartheta - \varphi )$

С учетом того, что $\left| {{\mathbf{r}} + {\mathbf{u}}} \right| \ll R$, преобразуем функционал (1.7), сохраняя квадратичные члены по ${\text{(}}{\mathbf{r}} + {\mathbf{u}}{\text{)/}}R$ и линейные по ${\mathbf{u}}{\text{/}}R$ к виду

(1.9)

$\Pi = - \frac{{\gamma m}}{R} + \frac{\gamma }{{{{R}^{2}}}}\int\limits_K {({\mathbf{\xi }},{\mathbf{u}})\rho ds} - \frac{{3\gamma }}{{{{R}^{3}}}}\int\limits_K {({\mathbf{\xi }},{\mathbf{r}})({\mathbf{\xi }},{\mathbf{u}})\rho ds} $

Функционалы потенциальной энергии упругих деформаций и диссипативных сил зададим выражениями

$E[{\mathbf{u}}] = \frac{N}{2}\int\limits_K {{{{\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{s}^{2}}}}} \right)}}^{2}}} ds,\quad D[{\mathbf{\dot {u}}}] = \frac{{\chi N}}{2}\int\limits_K {{{{\left( {\frac{{{{\partial }^{3}}u}}{{\partial t\partial {{s}^{2}}}}} \right)}}^{2}}} ds,$

где $N$ – изгибная жесткость стержня, $\chi $ – постоянная, характеризующая рассеяние энергии в стержне при изгибе ($\chi > 0$).

Уравнения движения выпишем в форме уравнений Рауса. Для этого от обобщенной скорости $\dot {\varphi }$ перейдем к обобщенному импульсу $I = {{\nabla }_{{\dot {\varphi }}}}T$. Учитывая второе равенство (1.5) и выражение (1.6), выделим в функционале кинетической энергии квадратичную и линейную части по $\dot {\varphi }$:

$T = {{T}_{0}} + {{T}_{1}} + {{T}_{2}}$

(1.10)

${{T}_{2}} = \frac{1}{2}J[{\mathbf{u}}]{{\dot {\varphi }}^{2}},\quad {{T}_{1}} = {{G}_{u}}\dot {\varphi },\quad {{T}_{0}} = \frac{1}{2}m{{{\mathbf{\dot {R}}}}^{2}} + \frac{1}{2}\int\limits_K {{{{{\mathbf{\dot {u}}}}}^{2}}\rho ds} + \int\limits_K {({{\Gamma }^{{ - 1}}}{\mathbf{\dot {R}}},{\mathbf{\dot {u}}})\rho ds} $

$J[{\mathbf{u}}] = \int\limits_V {{{{[{{{\mathbf{e}}}_{3}} \times ({\mathbf{r}} + {\mathbf{u}})]}}^{2}}} d\mu ,\quad {{G}_{u}} = \int\limits_K {({\mathbf{u}} \times {{\Gamma }^{{ - 1}}}{\mathbf{\dot {R}}} + ({\mathbf{r}} + {\mathbf{u}}) \times {\mathbf{\dot {u}}},{{{\mathbf{e}}}_{3}})\rho ds} $

Отсюда получаем

(1.11)

$I = J[{\mathbf{u}}]\dot {\varphi } + {{G}_{u}}$

Функционал Рауса имеет вид [2, 4]

(1.12)

$\mathcal{R} = \mathcal{R}{\text{[}}I,\varphi ,\dot {u},u,t{\text{]}} = {{T}_{2}} - {{T}_{0}} + \Pi + E[u]$

При этом в правой части равенства (1.12) необходимо выразить $\dot {\varphi }$ из соотношения (1.11).

Введя обозначения для координат вектора ${{\Gamma }^{{ - 1}}}{\mathbf{\dot {R}}}$ = $({{\eta }_{1}},{{\eta }_{2}},0)$:

(1.13)

${{\eta }_{1}} = \frac{{an}}{{\sqrt {1 - {{e}^{2}}} }}[\sin (\varphi - \vartheta ) + e\sin \varphi ],\quad {{\eta }_{2}} = \frac{{an}}{{\sqrt {1 - {{e}^{2}}} }}[\cos (\varphi - \vartheta ) + e\cos \varphi ]$

получим следующее выражение для функционала Рауса:

$\mathcal{R}[I,\varphi ,\dot {u},u,t] = \frac{1}{2}{{\left[ {A + \int\limits_K {{{u}^{2}}\rho ds} } \right]}^{{ - 1}}}{{\left[ {I - \int\limits_K {(s\dot {u} - u{{\eta }_{1}})\rho ds} } \right]}^{2}} - \frac{{m{{a}^{2}}{{n}^{2}}(1 + {{e}^{2}} + 2e\cos \vartheta )}}{{2(1 - {{e}^{2}})}} - $

$ - \;\frac{1}{2}\int\limits_K {{{{\dot {u}}}^{2}}\rho ds} - \int\limits_K {{{\eta }_{2}}\dot {u}\rho ds} - \frac{{\gamma m}}{R} + \frac{\gamma }{{{{R}^{2}}}}\int\limits_K {{{\xi }_{2}}u\rho ds} - \frac{{3\gamma }}{{{{R}^{3}}}}\int\limits_K {{{\xi }_{1}}{{\xi }_{2}}su\rho ds} + \frac{N}{2}\int\limits_K {{{{\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{s}^{2}}}}} \right)}}^{2}}ds} $

$A = \int\limits_V {(x_{1}^{2} + x_{3}^{2})d\mu = \int\limits_V {(x_{1}^{2} + x_{2}^{2})d\mu = \int\limits_V {(x_{2}^{2} + x_{3}^{2})d\mu } } } $

Здесь R и $\vartheta $ − заданные функции времени согласно соотношениям (1.3), $A$ − момент инерции спутника с недеформированными стержнями относительной оси $C{{x}_{i}}$ (i = 1, 2, 3).

Уравнения движения спутника записываются в форме уравнений Рауса

(1.14)

$\dot {I} = - {{\nabla }_{\varphi }}\mathcal{R},\quad \dot {\varphi } = {{\nabla }_{I}}\mathcal{R},\quad - {\kern 1pt} \frac{d}{{dt}}{{\nabla }_{{\dot {u}}}}\mathcal{R} + {{\nabla }_{u}}\mathcal{R} + {{\nabla }_{{\dot {u}}}}D = 0,$

т.е. в виде сложной системы интегро-дифференциальных уравнений. Конфигурационным пространством задачи является прямое произведение

$R \times {{V}_{0}},\quad {{V}_{0}} = \left\{ {y(s){\text{:}}\;y \in W_{2}^{2}(K),\;y( \pm b) = \frac{{dy( \pm b)}}{{ds}} = 0} \right\}$

$W_{2}^{2}(K)$ − пространство Соболева. Для дальнейшего исследования применяется метод разделения движений [6, 7], основанный на предположении, что время затухания собственных колебаний стержней на наинизшей частоте много больше периода этих колебаний и много меньше характерного времени движения спутника как механической системы в целом.

2. Построение возмущенной системы уравнений движения. Введем малый параметр

$\varepsilon = \omega _{0}^{2}{{d}^{4}}\rho {{N}^{{ - 1}}} \ll 1,$

где ${{\omega }_{0}}$ − постоянная, ограничивающая модуль начальной угловой скорости спутника. Можно выбрать масштабы размерных единиц так, чтобы $\omega _{0}^{2}{{d}^{4}}\rho = 1$, тогда $\varepsilon = {{N}^{{ - 1}}}$. Если $\varepsilon = 0$, то будем полагать $u \equiv 0$. Это означает, что стержни не деформируются и спутник движется как твердое тело. В этом случае функционал Рауса имеет вид

$\mathcal{R}[I,\varphi ,0,0,t] = \frac{{{{I}^{2}}}}{{2A}} - \frac{{\gamma m(3 + 4e\cos \vartheta + {{e}^{2}})}}{{2a(1 - {{e}^{2}})}}$

Уравнения невозмущенного движения выглядят следующим образом

(2.1)

$\dot {I} = 0,\quad \dot {\varphi } = \frac{I}{A}$

При $\varepsilon \ne 0$ после затухания собственных колебаний вязкоупругих стержней, согласно методу разделения движений [4, 6], решение последнего уравнения (1.14) будем искать в виде разложений по малому параметру $\varepsilon $:

$u(s,t) = \varepsilon {{u}_{1}}(s,t) + {{\varepsilon }^{2}}{{u}_{2}}(s,t) + \cdots $

Для функции ${{u}_{1}}(s,t)$ первого приближения по $\varepsilon $ получим

(2.2)

$B({{u}_{1}} + \chi {{\dot {u}}_{1}}) = \frac{d}{{dt}}\left[ { - \rho s\frac{I}{A} - \rho {{\eta }_{2}}} \right] - \rho {{\eta }_{1}}\frac{I}{A} - \frac{\gamma }{{{{R}^{2}}}}\rho {{\xi }_{2}} + 3\frac{\gamma }{{{{R}^{3}}}}\rho s{{\xi }_{1}}{{\xi }_{2}}$

Здесь $B$ − дифференциальный оператор, порожденный дифференциальным выражением $B(y)$ = ${{d}^{4}}y{\text{/}}d{{s}^{4}}$ и краевыми условиями

$y( \pm b) = \frac{{dy( \pm b)}}{{ds}} = 0,\quad \frac{{{{d}^{2}}y( \pm (b + d))}}{{d{{s}^{2}}}} = \frac{{{{d}^{3}}y( \pm (b + d))}}{{d{{s}^{3}}}} = 0$

Переменные I и $\varphi $ в правой части уравнения (2.2) − решения невозмущенной системы уравнений (2.1). Используя соотношения (1.3), (1.8), (1.13) и (2.1), преобразуем уравнение (2.2) к виду

(2.3)

$B({{u}_{1}} + \chi {{\dot {u}}_{1}}) = sf(t);\quad f(t) = - \frac{{3\rho \gamma }}{{2{{R}^{3}}}}\sin 2\beta ,\quad \beta = \varphi - \vartheta $

Частное решение уравнения (2.3), установившееся после затухания собственных колебаний стержней, можно представить в виде ряда [2, 4]

(2.4)

${{u}_{1}}(s,t) = \sum\limits_{n = 0}^\infty {{{{( - \chi )}}^{n}}} \frac{{{{\partial }^{n}}{{u}_{{10}}}}}{{\partial {{t}^{n}}}};\quad {{u}_{{10}}}(s,t) = {{B}^{{ - 1}}}(sf(t))$

Ограничиваясь двумя первыми членами ряда, получим решение уравнения (2.3) в виде

(2.5)

${{u}_{1}}(s,t) = \Psi (s)\{ f - \chi \dot {f}\} $

В правой части равенства (2.5) дифференцирование по времени производится в силу невозмущенной системы уравнений (2.1), т.е.

(2.6)

$\dot {f} = \frac{{\partial f}}{{\partial \varphi }}\frac{I}{A} + \frac{{\partial f}}{{\partial \vartheta }}\dot {\vartheta }$

при учете соотношений (1.3). Функция $\Psi \left( s \right)$ − нечетная [2]:

(2.7)

$\int\limits_K {\Psi (s)ds} = 0,\quad \int\limits_K {s\Psi (s)ds} = {{d}_{1}} > 0$

На следующем шаге необходимо линеаризовать правые части системы двух первых уравнений (1.14) по $u$ и $\dot {u}$ и подставить полученное приближенное решение $\varepsilon {{u}_{1}}(s,t)$. В результате возмущенная система уравнений движения спутника примет вид

(2.8)

$\dot {I} = - \frac{{3\varepsilon \rho {{d}_{1}}\gamma }}{{{{R}^{3}}}}(f - \chi \dot {f})\cos 2\beta ,\quad \dot {\varphi } = \frac{I}{A} - \frac{{\varepsilon \rho {{d}_{1}}}}{A}(\dot {f} - \chi \ddot {f})$

Введем безразмерную переменную $k = I{\text{/}}(An)$, приближенно равную отношению собственной угловой скорости вращения спутника к среднему движению по орбите, и используем обозначения (1.3). Тогда из системы (2.8) с учетом равенств (2.6) получим следующую систему уравнений возмущенного движения спутника:

$\dot {k} = {{\varepsilon }_{1}}n{{F}_{1}}(k,\beta ,\vartheta ),\quad \dot {\varphi } = kn + {{\varepsilon }_{1}}n{{F}_{2}}(k,\beta ,\vartheta ),\quad \dot {l} = n$

${{F}_{1}}(k,\beta ,\vartheta ) = \frac{{3{{p}^{6}}}}{{4{{q}^{6}}}}\{ (1 + 3\chi ne{{p}^{{ - 1}}}\sigma \sin \vartheta )\sin 4\beta - 4\chi n(k - \sigma ){{\cos }^{2}}2\beta \} $

(2.9)

$\begin{gathered} {{F}_{2}}\left( {k,\beta ,\vartheta } \right) = \frac{{{{p}^{3}}}}{{2{{q}^{3}}}}\{ - 3e{{p}^{{ - 1}}}\sigma \sin \vartheta \sin 2\beta + 2\left( {k - \sigma } \right)\cos 2\beta + \\ + \;\chi n[3e{{p}^{{ - 2}}}{{\sigma }^{2}}(p\cos \vartheta - 4e{{\sin }^{2}}\vartheta )\sin 2\beta + \\ \end{gathered} $

$ + \;4e{{p}^{{ - 1}}}\sigma \sin \vartheta (3k - 4\sigma )\cos 2\beta + 4{{(k - \sigma )}^{2}}\sin 2\beta ]\} $

${{\varepsilon }_{1}} = 3\varepsilon {{A}^{{ - 1}}}{{\rho }^{2}}{{d}_{1}}{{n}^{2}} \ll 1,\quad \vartheta = \vartheta (l),\quad \beta = \varphi - \vartheta (l)$

3. Эволюционная система уравнений движения вблизи резонанса 1:1. Проведем процедуру усреднения возмущенной системы уравнений (2.9) вблизи резонанса 1:1, когда значения переменной $k$ близки к единице. В правые части первых двух уравнений системы (2.9) средняя аномалия входит неявным образом через истинную аномалию. При малых значениях эксцентриситетов справедливы равенства [1]

$\vartheta = l + 2e\sin l + \frac{5}{4}{{e}^{2}}\sin 2l + o({{e}^{2}})$

$\sin \vartheta = \sin l + e\sin 2l + \frac{9}{8}{{e}^{2}}\left( {\sin 3l - \frac{7}{9}\sin l} \right) + o({{e}^{2}})$

$\cos \vartheta = \cos l + e(\cos 2l - 1) + \frac{9}{8}{{e}^{2}}(\cos 3l - \cos l) + o({{e}^{2}})$

Введем полубыструю переменную $\psi = \varphi - l$ [8]. Вблизи резонанса 1:1 переменная $\psi $ становится медленной. Далее проведем усреднение только по одной быстрой угловой переменной – средней аномалии $l$. Полученная в результате указанных преобразований система уравнений движения спутника

(3.1)

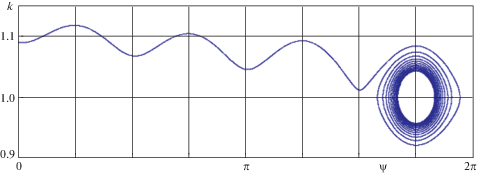
$\begin{gathered} \dot {k} = \frac{{3{{\varepsilon }_{1}}n}}{4}\left\{ {\left( {1 - \frac{{17}}{2}{{e}^{2}}} \right)\sin 4\psi - 2\chi n\left[ {(k - 1)\left( {1 - \frac{{17}}{2}{{e}^{2}}} \right)\cos 4\psi + (k - 1) + \frac{3}{2}{{e}^{2}}(5k - 9)} \right]} \right\} \\ \dot {\psi } = n(k - 1) + {{\varepsilon }_{1}}n(k - 1)\{ \cos 2\psi + 2\chi n(k - 1)\sin 2\psi \} \left( {1 - \frac{5}{2}{{e}^{2}}} \right) \\ \end{gathered} $

имеет две серии стационарных решений:

$1)\quad k = 1,\quad \psi = - \frac{\alpha }{4} + \frac{{\pi m}}{2},\quad m \in Z,\quad 2)\quad k = 1,\quad \psi = \frac{\pi }{4} + \frac{\alpha }{4} + \frac{{\pi m}}{2},\quad m \in Z$

$\alpha = \arcsin \frac{{12\chi n{{e}^{2}}}}{{1 - {{17{{e}^{2}}} \mathord{\left/ {\vphantom {{17{{e}^{2}}} 2}} \right. \kern-0em} 2}}},\quad 0 < \alpha \ll 1$

Первая серия соответствует движению спутника, при котором он все время обращен одной стороной к притягивающему центру, а стержни либо почти направлены к притягивающему центру, либо почти перпендикулярны радиус-вектору центра масс. Вторая серия соответствует движению спутника в резонансе 1:1, когда угол между его осью симметрии и прямой, соединяющей его центр масс с притягивающим центром, близок к значению π/4 или –π/4.

Проведенный анализ устойчивости полученных стационарных решений на основе линеаризованных уравнений показал, что стационарные решения первой серии неустойчивы, а второй серии – асимптотически устойчивы.

На фиг. 2 представлена интегральная кривая системы уравнений (3.1) в плоскости ($k$, $\psi $) для следующих начальных данных и значений параметров:

$k(0) = 1.09,\quad \psi (0) = 0,\quad {{\varepsilon }_{1}} = 0.01,\quad \chi n = 0.8,\quad e = 0.01$

построенная в среде Octave. Интегрирование проводилось на отрезке времени, соответствующем 100 оборотам спутника вокруг притягивающего центра. Как видно из графика, угол $\psi $ сначала монотонно увеличивается, а затем происходит захват в резонанс около значения $\psi = 7{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$

Фиг. 2

Список литературы

Murray C.D., Dermott S.F. Solar System Dynamics. Cambridge: Univ. Press, 1999. 592 p. = Мюррей К., Дермотт С. Динамика Солнечной системы. М.: Физматлит, 2010. 588 с.
Вильке В.Г., Шатина А.В. Эволюция движения симметричного спутника с гибкими вязкоупругими стержнями в центральном ньютоновском поле сил // Космич. иссл. 1999. Т. 37. Вып. 3. С. 289−295.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965. 416 с.
Вильке В.Г. Аналитическая механика систем с бесконечным числом степеней свободы. Ч. 1, 2. М.: Изд-во мех.-мат. фак. МГУ, 1997. Ч. 1. 216 с. Ч. 2. 160 с.
Амелькин Н.И. Об асимптотических свойствах движений спутников в центральном поле, обусловленных внутренней диссипацией // ПММ. 2011. Т. 75. Вып. 2. С. 205−223.
Вильке В.Г. Разделение движений и метод усреднения в механике систем с бесконечным числом степеней свободы // Вестн. МГУ. Сер. 1. Матем., мех. 1983. Вып. 5. С. 54−59.
Черноусько Ф.Л. О движении твердого тела с упругими и диссипативными элементами // ПММ. 1978. Т. 42. Вып. 1. С. 34−42.
Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики. М.: Эдиториал УРСС, 2009. 416 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал