1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 1, 2019

Прикладная математика и механика, 2019, T. 83, № 1, стр. 126-133

УПРОЩЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ПОПЕРЕЧНОГО ИЗГИБА УПРУГИХ МИКРОПОЛЯРНЫХ ПЛАСТИН

С. В. Варданян *

Московский государственный университет им. М.В. Ломоносова
Москва, Россия

* E-mail: vardanyan.sedrak@gmail.com

Поступила в редакцию 29.08.2016

Полный текст (PDF)

Аннотация

Предлагается метод, позволяющий значительно упростить решение задачи поперечного изгиба микрополярных пластин в рамках микрополярной теории упругости. Он может быть применен в инженерных расчетах микрополярных конструкций. Расчет напряженно-деформированного состояния упрощается введением одной функции, которая приводит систему уравнений к более удобному для расчетов виду. В качестве примера исследуется напряженно-деформированное состояние длинной прямоугольной пластины при разных граничных условиях. Приводятся графики прогибов как при учете эффекта микрополярности, так и в рамках классической теории.

Ключевые слова: микрополярная пластина, поперечный изгиб, упрощенное решение

Аналитические методы решения задач изгиба пластин разделяются на связанные с точным пространственным подходом, предложенным Новацким [1, 2], и с подходами, основанными на использовании определенных гипотез, таких как гипотезы Кирхгофа [3, 4], Миндлина [5], Рейснера [6], Амбарцумяна [7]. Теория микрополярных оболочек развита Л.М. Зубовым и В.А. Еремеевым [8]; исследованы конечные деформации несжимаемых изотропных микрополярных материалов [9], рассмотрено равновесие нелинейно-упругих микрополярных тел [10].

Исследованию поведения пластин в условиях изгиба с применением метода конечных элементов посвящены работы Г.А. Геворкяна [11], причем с помощью предложенного автором метода задачи приводятся к задачам квадратичного программирования, что позволяет сформулировать постановки более сложных граничных задач с выполнением условий непрерывности перемещений и напряжений при разных граничных условиях. Этот метод распространен на задачи изгиба в рамках микрополярной теории пластин [12–14].

Детально был представлен другой численный метод решения задач изгиба пластин – метод граничных элементов [15]. Существуют также предложения по оптимизации алгоритма расчетов пластин (см., например, [16]).

Полученные разными авторами результаты позволили существенно развить теорию изгиба микрополярных пластин. Известны многочисленные экспериментальные работы в этом направлении. Современное развитие техники позволяет проводить эксперименты, решающие многофункциональные задачи с высокой точностью (см., например, [17]).

В отличие от классической изотропной теории упругости в микрополярной теории упругости имеется шесть независимых постоянных материала. С использованием экспериментальных методов [18–22] уточнялся их физический смысл, а также определялись значения этих постоянных. Следует отметить также работы ([23, 24] и др.) по изучению механических характеристик с использованием экспериментальных методов. Кроме экспериментальных методов существуют и другие способы определения параметров процесса. Однако значения этих параметров известны далеко не для всех материалов.

1. Постановка задачи. Рассматривается упругая микрополярная пластина постоянной толщины $h$. Система координат вводится таким образом, чтобы средняя плоскость пластины совпала с плоскостью координат $xOy$, а координатная ось $z$ была перпендикулярна к срединной плоскости. Среда дискретной структуры трактуется как сплошная. Предположим, что силовые воздействия на элементарной площадке дифференциального элемента осуществляются как главным силовым, так и главным моментным векторами [25]. Главный вектор внешних сил выражается через компоненты тензора напряжений ${{\sigma }_{{ij}}}$, а главный момент внешних сил – через компоненты тензора моментных напряжений ${{\mu }_{{ij}}}$ ($i,j = 1,2,3$), причем оба тензора несимметричные. В каждой точке элементарной частицы имеются объемные силы и объемные моменты, представляемые векторами $f = f({{f}_{1}},{{f}_{2}},{{f}_{3}})$ и $g = g({{g}_{1}},{{g}_{2}},{{g}_{3}})$, соответственно.

Уравнения равновесия и закон малых упругих деформаций с учетом моментных напряжений можно представить в виде

(1.1)
$\begin{gathered} {{\sigma }_{{ji,j}}} + {{f}_{i}} = 0,\quad {{ \in }_{{ijk}}}{{\sigma }_{{jk}}} + {{\mu }_{{ji,j}}} + {{g}_{i}} = 0 \\ {{\sigma }_{{ji}}} = \left( {\mu + \alpha } \right){{\gamma }_{{ji}}} + \left( {\mu - \alpha } \right){{\gamma }_{{ij}}} + \lambda {{\gamma }_{{ii}}}{{\delta }_{{ij}}},\quad {{\mu }_{{ji}}} = \left( {\gamma + \varepsilon } \right){{\chi }_{{ji}}} + \left( {\gamma - \varepsilon } \right){{\chi }_{{ij}}} + \beta {{\chi }_{{ii}}}{{\delta }_{{ij}}}, \\ \end{gathered} $
где ${{ \in }_{{ijk}}}$ – компоненты тензора Леви-Чивиты, ${{\chi }_{{ij}}}$ – компоненты тензора изгиба–кручения, ${{\delta }_{{ij}}}$ – символ Кронекера, $\lambda $ и $\mu $ – параметры Ламе, $\alpha $, $\gamma $, $\beta $, $\varepsilon $ – упругие постоянные микрополярности.

В предположении, что плоскости $z = \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}$ загружены поверхностными силами, a внешние моментные воздействия на них отсутствуют, граничные условия записываются в виде

(1.2)
$\begin{gathered} z = \pm h{\text{/}}2:\quad {{\sigma }_{{zz}}} = \pm {{Z}^{ \pm }},\quad {{\sigma }_{{31}}} = \pm {{X}^{ \pm }},\quad {{\sigma }_{{32}}} = \pm {{Y}^{ \pm }}, \\ {{\mu }_{{33}}} = 0,\quad {{\mu }_{{31}}} = 0,\quad {{\mu }_{{32}}} = 0 \\ \end{gathered} $
где ${{X}^{ \pm }}(x,y)$, ${{Y}^{ \pm }}(x,y)$ и ${{Z}^{ \pm }}(x,y)$ тангенциальные и нормальные компоненты векторов интенсивности поверхностных сил, приложенных соответственно на плоскостях $z = \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}$.

Гипотезы, на которых основана теория пластин, опираются на исследования С.А. Амбарцумяна [25–27] и заключаются в следующем:

1) нормальные к срединной плоскости пластины, перемещение $w$ и поворот ${{\omega }_{3}}$ не зависят от координаты $z$;

2) касательные напряжения ${{\sigma }_{{xz}}}$ и ${{\sigma }_{{yz}}}$ по толщине пластины меняются по заданному закону;

3) силовые ${{\sigma }_{{zx}}}$, ${{\sigma }_{{zy}}}$, ${{\sigma }_{{zz}}}$ и моментные ${{\mu }_{{zx}}}$, ${{\mu }_{{zy}}}$, ${{\mu }_{{zz}}}$ напряжения пренебрежимо малы.

Принимаем следующие обозначения:

$A = \gamma + \varepsilon + D{\text{/}}h$
${{A}_{1}} = (\mu + \alpha )(\gamma + \varepsilon ) + 12D\frac{\alpha }{{5h}},\quad {{A}_{2}} = (\mu + \alpha )\left( {2\gamma + \beta + \frac{\alpha }{5}{{h}^{2}}} \right)$
(1.3)
${{A}_{3}} = 12D\nu \frac{\alpha }{{5h}} + \frac{{\alpha (\mu - \alpha )}}{5}{{h}^{2}} - (\mu + \alpha )(\gamma + \beta - \varepsilon )$
$B = \frac{E}{{1 - {{\nu }^{2}}}},\quad {{B}_{{12}}} = \frac{{E\nu }}{{1 - {{\nu }^{2}}}},\quad D = \frac{E}{{12(1 - {{\nu }^{2}})}}{{h}^{3}}$
${{X}_{1}} = \frac{1}{2}({{X}^{ + }} - {{X}^{ - }}),\quad {{X}_{2}} = {{X}^{ + }} + {{X}^{ - }}\quad (X \leftrightarrow Y),\quad {{Z}_{2}} = {{Z}^{ + }} + {{Z}^{ - }}$
$E$ – модуль упругости, $\nu $ – коэффициент Пуассона, $D$ – жесткость пластины при изгибе, без учета моментных напряжений.

Согласно указанным гипотезам, уравнения поперечного изгиба (${{X}^{ \pm }} = 0$, ${{Y}^{ \pm }} = 0$) микрополярной пластины можно представить относительно искомых функций $w(x,y)$ и ${{\psi }_{i}}(x,y)$ ($i = 1,2$) в виде

(1.4)
$({{\psi }_{{1x}}} + {{\psi }_{{2y}}}){{\alpha {{h}^{3}}} \mathord{\left/ {\vphantom {{\alpha {{h}^{3}}} {12}}} \right. \kern-0em} {12}} = - {{Z}_{2}}$
(1.5)
$A\Delta {{w}_{x}} - ({{A}_{1}}\Delta {{\psi }_{{1xx}}} - {{A}_{3}}({{\psi }_{{1yy}}} - {{\psi }_{{1xy}}})){{h}^{2}}{\text{/}}(48\mu ) + {{\psi }_{1}}\alpha {{h}^{2}}{\text{/}}12 = 0\quad (1 \leftrightarrow 2,x \leftrightarrow y)$

Предполагается, что ${{Z}_{2}} = q$ – равномерно распределенная нагрузка, и учтено, что, согласно обозначениям (1.3), ${{A}_{2}} = {{A}_{1}} - {{A}_{3}}$.

Имеем следующие соотношения [25]:

для внутренних усилий и моментов

(1.6)
$\begin{gathered} {{N}_{{xz}}} = {{\psi }_{1}}{{\alpha {{h}^{3}}} \mathord{\left/ {\vphantom {{\alpha {{h}^{3}}} {12}}} \right. \kern-0em} {12}} \\ {{M}_{{xx}}} = - D({{w}_{{xx}}} + \nu {{w}_{{yy}}}) + ({{\psi }_{{1x}}} + \nu {{\psi }_{{2y}}}){{D\alpha {{h}^{2}}} \mathord{\left/ {\vphantom {{D\alpha {{h}^{2}}} {(20\mu )}}} \right. \kern-0em} {(20\mu )}} \\ {{H}_{{xy}}} = - {{w}_{{xy}}}{{2\mu {{h}^{3}}} \mathord{\left/ {\vphantom {{2\mu {{h}^{3}}} {12}}} \right. \kern-0em} {12}} + ({{\psi }_{{2x}}} + \bar {\eta }{{\psi }_{{1y}}}){{\alpha {{h}^{5}}(\mu + \alpha )} \mathord{\left/ {\vphantom {{\alpha {{h}^{5}}(\mu + \alpha )} {(240\mu )}}} \right. \kern-0em} {(240\mu )}} \\ \bar {\eta } = {{(\mu - \alpha )} \mathord{\left/ {\vphantom {{(\mu - \alpha )} {(\mu - \alpha )}}} \right. \kern-0em} {(\mu - \alpha )}} \\ \end{gathered} $
для моментов вследствие моментных напряжений
(1.7)
$\begin{gathered} {{P}_{{xx}}} = 2\gamma h{{w}_{{xy}}} - ((2\gamma + \beta ){{\psi }_{{2x}}} - \beta {{\psi }_{{1y}}}){{{{h}^{3}}(\mu + \alpha )} \mathord{\left/ {\vphantom {{{{h}^{3}}(\mu + \alpha )} {(48\mu )}}} \right. \kern-0em} {(48\mu )}} \\ {{R}_{{xy}}} = - (\gamma + \varepsilon )h({{w}_{{xx}}} - \eta {{w}_{{yy}}}) + ({{\psi }_{{1x}}} - \eta {{\psi }_{{2y}}}){{{{h}^{2}}(\mu + \alpha )(\gamma + \varepsilon )} \mathord{\left/ {\vphantom {{{{h}^{2}}(\mu + \alpha )(\gamma + \varepsilon )} {(48\mu )}}} \right. \kern-0em} {(48\mu )}} \\ \eta = {{(\gamma - \varepsilon )} \mathord{\left/ {\vphantom {{(\gamma - \varepsilon )} {(\gamma + \varepsilon )}}} \right. \kern-0em} {(\gamma + \varepsilon )}} \\ \end{gathered} $
для двух компонент тензора поворота ${{\omega }_{1}}$ и ${{\omega }_{2}}$

(1.8)
${{\omega }_{1}} = {{w}_{y}} - ({{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} 4}} \right. \kern-0em} 4} - {{z}^{2}})(\mu + \alpha ){{{{\psi }_{2}}} \mathord{\left/ {\vphantom {{{{\psi }_{2}}} {(8\mu )}}} \right. \kern-0em} {(8\mu )}}$

Все формулы (1.6)–(1.8) дополняются соотношениями по правилу ($1 \leftrightarrow 2$, $x \leftrightarrow y$).

2. Метод решения. Решение уравнений равновесия (1.4), (1.5), характеризующих изгиб микрополярной пластины будем искать по ранее предложенному методу [12], вводя функцию $F$ следующим образом:

(2.1)
${{\psi }_{1}} = - {{12A\Delta {{F}_{x}}} \mathord{\left/ {\vphantom {{12A\Delta {{F}_{x}}} {(\alpha {{h}^{2}})}}} \right. \kern-0em} {(\alpha {{h}^{2}})}}\quad (1 \leftrightarrow 2,x \leftrightarrow y),\quad w = F - {{{{A}_{1}}\Delta F} \mathord{\left/ {\vphantom {{{{A}_{1}}\Delta F} {(4\mu \alpha )}}} \right. \kern-0em} {(4\mu \alpha )}}$

Тогда тождественно выполняются уравнения (1.5), а из уравнения (1.4) получим

(2.2)
${{D}_{1}}\Delta \Delta F = {{Z}_{2}};\quad {{D}_{1}} = D + \left( {\varepsilon + \gamma } \right)h$

Учитывая связи (2.1) и исходя из соотношений (1.6), (1.7), для внутренних усилий и моментов имеем (в приведенных ниже соотношениях (2.3) $x \leftrightarrow y$)

(2.3)
$\begin{gathered} {{N}_{{xz}}} = - {{D}_{1}}\Delta {{F}_{x}} \\ {{M}_{{xx}}} = - D({{F}_{{xx}}} + \nu {{F}_{{yy}}}) + {{D(\gamma + \varepsilon )(5\mu - 7\alpha )(\Delta {{F}_{{xx}}} + \nu \Delta {{F}_{{yy}}})} \mathord{\left/ {\vphantom {{D(\gamma + \varepsilon )(5\mu - 7\alpha )(\Delta {{F}_{{xx}}} + \nu \Delta {{F}_{{yy}}})} {\left( {20\mu \alpha } \right)}}} \right. \kern-0em} {\left( {20\mu \alpha } \right)}} \\ {{H}_{{xy}}} = D(1 - \nu ){{F}_{{xy}}} + {{{{h}^{3}}(\gamma + \varepsilon )(5\mu - 7\alpha )\Delta {{F}_{{xy}}}} \mathord{\left/ {\vphantom {{{{h}^{3}}(\gamma + \varepsilon )(5\mu - 7\alpha )\Delta {{F}_{{xy}}}} {\left( {120\alpha } \right)}}} \right. \kern-0em} {\left( {120\alpha } \right)}} \\ {{P}_{{xx}}} = 2\gamma h{{F}_{{xy}}} + {{D\left( {5\mu - 7\alpha } \right)\Delta {{F}_{{xy}}}} \mathord{\left/ {\vphantom {{D\left( {5\mu - 7\alpha } \right)\Delta {{F}_{{xy}}}} {\left( {5h} \right)}}} \right. \kern-0em} {\left( {5h} \right)}} \\ {{R}_{{xy}}} = - (\gamma + \varepsilon )h({{F}_{{xx}}} - \eta {{F}_{{yy}}}) - {{D(\gamma + \varepsilon )(5\mu - 7\alpha )(\Delta {{F}_{{xx}}} - \eta \Delta {{F}_{{yy}}})} \mathord{\left/ {\vphantom {{D(\gamma + \varepsilon )(5\mu - 7\alpha )(\Delta {{F}_{{xx}}} - \eta \Delta {{F}_{{yy}}})} {\left( {20\mu \alpha } \right)}}} \right. \kern-0em} {\left( {20\mu \alpha } \right)}}, \\ \end{gathered} $
а исходя из соотношений (1.8) и обозначения (1.3), для двух компонент тензора поворота ${{\omega }_{1}}$ и ${{\omega }_{2}}$ при $z = 0$ получим

(2.4)
${{\omega }_{1}} = {{F}_{y}} + \left( {{{\left( {\mu + \alpha } \right)\left( {\gamma + \varepsilon } \right)} \mathord{\left/ {\vphantom {{\left( {\mu + \alpha } \right)\left( {\gamma + \varepsilon } \right)} {\left( {8\mu \alpha } \right)}}} \right. \kern-0em} {\left( {8\mu \alpha } \right)}} - {{3D\left( {3\alpha - 5\mu } \right)} \mathord{\left/ {\vphantom {{3D\left( {3\alpha - 5\mu } \right)} {\left( {40h\mu \alpha } \right)}}} \right. \kern-0em} {\left( {40h\mu \alpha } \right)}}} \right)\Delta {{F}_{y}}\quad (1 \leftrightarrow 2,x \leftrightarrow y)$

Таким образом, задача поперечного изгиба пластины сведена к интегрированию дифференциального уравнения (2.2) с соответствующими граничными условиями. Если решение этого уравнения известно, то изгибающие (${{M}_{{xx}}} + {{R}_{{xy}}}$, ${{M}_{{yy}}} + {{R}_{{yx}}}$) и крутящие (${{H}_{{xy}}} + {{P}_{{xx}}}$, ${{H}_{{yx}}} + {{P}_{{yy}}}$) моменты, а также поперечные силы (${{N}_{{zx}}}$, ${{N}_{{yz}}}$) могут быть вычислены из соотношений (2.3).

Обозначив

${{M}_{x}} = {{M}_{{xx}}} + {{R}_{{xy}}},\quad {{M}_{{xy}}} = {{H}_{{xy}}} + {{P}_{{xx}}},\quad (x \leftrightarrow y),$
при учете соотношений (2.3) находим
(2.5)
${{M}_{x}} = - {{D}_{1}}{{F}_{{xx}}} - {{D}_{2}}{{F}_{{yy}}} + {{D}_{3}}\Delta {{F}_{{yy}}},\quad {{M}_{{xy}}} = {{D}_{4}}{{F}_{{xy}}} + ({{D}_{5}} + {{D}_{6}})\Delta {{F}_{{xy}}}\quad (x \leftrightarrow y)$
(2.6)
${{\omega }_{1}} = {{F}_{y}} + {{D}_{7}}\Delta {{F}_{y}}\quad (x \leftrightarrow y),$
где введены следующие обозначения для коэффициентов, содержащих упругие постоянные материала пластины:

(2.7)
$\begin{gathered} {{D}_{2}} = D\nu + \left( {\varepsilon - \gamma } \right)h,\quad {{D}_{3}} = {{D\left( {\gamma + \varepsilon } \right)\left( {5\mu - 7\alpha } \right)\left( {\nu + \eta } \right)} \mathord{\left/ {\vphantom {{D\left( {\gamma + \varepsilon } \right)\left( {5\mu - 7\alpha } \right)\left( {\nu + \eta } \right)} {\left( {20\mu \alpha } \right)}}} \right. \kern-0em} {\left( {20\mu \alpha } \right)}} \\ {{D}_{4}} = D\left( {1 - \nu } \right) - 2h\gamma ,\quad {{D}_{5}} = \left( {5\mu - 7\alpha } \right){{{{h}^{3}}\left( {\gamma + \varepsilon } \right)} \mathord{\left/ {\vphantom {{{{h}^{3}}\left( {\gamma + \varepsilon } \right)} {\left( {120\alpha } \right)}}} \right. \kern-0em} {\left( {120\alpha } \right)}} \\ {{D}_{6}} = \left( {5\mu - 7\alpha } \right){D \mathord{\left/ {\vphantom {D {5h}}} \right. \kern-0em} {5h}},\quad {{D}_{7}} = {{\left( {\mu + \alpha } \right)\left( {\gamma + \varepsilon } \right)} \mathord{\left/ {\vphantom {{\left( {\mu + \alpha } \right)\left( {\gamma + \varepsilon } \right)} {\left( {8\mu \alpha } \right)}}} \right. \kern-0em} {\left( {8\mu \alpha } \right)}} - {{3D\left( {3\alpha - 5\mu } \right)} \mathord{\left/ {\vphantom {{3D\left( {3\alpha - 5\mu } \right)} {\left( {40h\mu \alpha } \right)}}} \right. \kern-0em} {\left( {40h\mu \alpha } \right)}} \\ \end{gathered} $

Подставляя в выражения для составляющих перерезывающей силы

(2.8)
${{N}_{x}} = {{N}_{{xz}}} - {{M}_{{xy}}}_{y}\quad \left( {x \leftrightarrow y} \right)$
значения поперечных сил и крутящих моментов, получим

(2.9)
${{N}_{x}} = - {{D}_{1}}\Delta {{F}_{x}} - \left( {{{D}_{4}} + {{D}_{5}} - {{D}_{6}}} \right)\Delta {{F}_{{xyy}}}\quad \left( {x \leftrightarrow y} \right)$

Рассмотрим длинную прямоугольную пластину, на которую действует распределенная нагрузка ${{Z}_{2}} = q$. Предположим, что пластина однородно закреплена по длинным сторонам, а короткие стороны закреплены произвольно (фиг. 1). Помещая начало координат на длинной стороне вдали от коротких сторон пластины и направляя ось $y$ вдоль длинной стороны, можно считать, что искомые величины для изгибаемой пластины $w$, ${{\psi }_{1}}$, ${{\psi }_{2}}$ зависят лишь от координаты $x$. Тогда из уравнения (2.2) получим

(2.10)
$F = \frac{q}{{24{{D}_{1}}}}{{x}^{4}} + \frac{{{{C}_{1}}}}{6}{{x}^{3}} + \frac{{{{C}_{2}}}}{2}{{x}^{2}} + {{C}_{3}}x + {{C}_{4}},$
где ${{C}_{1}}, \ldots ,{{C}_{4}}$ – постоянные интегрирования.

Фиг. 1

Рассмотрим несколько типов граничных условий, вводя обозначения

${{\tilde {A}}_{1}} = {{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {\left( {4\mu \alpha } \right)}}} \right. \kern-0em} {\left( {4\mu \alpha } \right)}},\quad \tilde {q} = {q \mathord{\left/ {\vphantom {q {\left( {24{{D}_{1}}} \right)}}} \right. \kern-0em} {\left( {24{{D}_{1}}} \right)}}$

Края пластины жестко защемлены. В случае, когда края пластины жестко защемлены, прогибы и соответствующие углы поворота вокруг контурных линий краев равны нулю и граничные условия записываются в виде

$x = 0,a{\text{:}}\quad w = 0,\quad {{\omega }_{2}} = 0,\quad {\text{и л и }}\quad F - {{\tilde {A}}_{1}}{{F}_{{xx}}} = {{F}_{x}} + {{D}_{7}}{{F}_{{xxx}}} = 0$

Отсюда находим постоянные интегрирования и получаем

(2.11)
$w = [{{x}^{3}} - 2a{{x}^{2}} + ({{a}^{2}} - 12{{D}_{7}} - 12{{\tilde {A}}_{1}})x + 12a({{D}_{7}} + {{\tilde {A}}_{1}})]\tilde {q}x$

Края пластины шарнирно оперты. В случае, когда края пластины шарнирно оперты, прогибы и изгибающие моменты по этим краям равны нулю, и граничные условия записываются в виде

$x = 0,a{\text{:}}\quad w = {{M}_{x}} = 0,\quad {\text{и л и }}\quad F - {{\tilde {A}}_{1}}{{F}_{{xx}}} = {{F}_{{xx}}} = 0$

Отсюда находим постоянные интегрирования и получаем

(2.12)
$w = [{{x}^{2}}(x - 2a) + {{a}^{3}} + 12{{\tilde {A}}_{1}}(a - x)]\tilde {q}x$

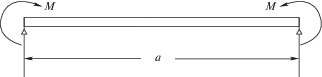
Чистый изгиб пластины. В случае чистого изгиба шарнирно опертая пластина загружена по длинным сторонам равномерно распределенными моментами с интенсивностью $M$ (фиг. 2). Граничные условия можно записать в форме

$x = 0,a{\text{:}}\quad w = 0,\quad {{M}_{x}} = M$
Фиг. 2

Отсюда получаем

(2.13)
$w = \left( {x - 2a} \right)\tilde {q}{{x}^{3}} + {{M{{x}^{2}}} \mathord{\left/ {\vphantom {{M{{x}^{2}}} 2}} \right. \kern-0em} 2} + (\tilde {q}{{a}^{3}} - {{Ma} \mathord{\left/ {\vphantom {{Ma} 2}} \right. \kern-0em} 2})x + 12{{\tilde {A}}_{1}}\tilde {q}x\left( {a - x} \right)$

Классической теории соответствуют выражения (2.11)–(2.13) при ${{\tilde {A}}_{1}} = 0$, ${{D}_{7}} = 0$ и $\tilde {q} = q{\text{/}}(24D)$.

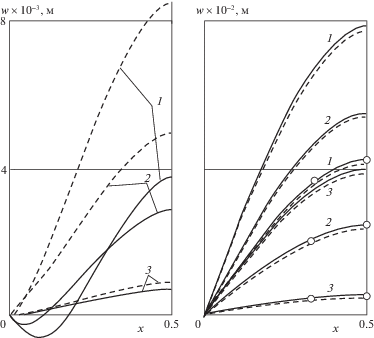
3. Анализ результатов. В целях анализа полученных результатов рассмотрим графики функции перемещения $w(x)$ в микрополярной и классической теориях изгиба пластин.

Рассмотрим разные материалы, микрополярные параметры которых представлены Лейксом [20, 22]. Для определения микрополярных постоянных имеем

(3.1)
$\alpha = \frac{{{{N}^{2}}\gamma }}{{2l_{b}^{2}(1 - {{N}^{2}})}},\quad \beta = 2\mu (l_{t}^{2} - 2l_{b}^{2}),\quad \gamma = 4l_{b}^{2}\mu ,\quad \varepsilon = \frac{{(\beta + \gamma )(1 - \Psi )}}{\Psi },$
где ${{l}_{b}}$ – характерная ширина при кручении, ${{l}_{t}}$ – при изгибе, $N$ – моментное число, $\Psi $ – полярный коэффициент. Значения этих величин определены экспериментально, они приведены в таблице 1 с указанием номеров соответствующих кривых на фиг. 3.

Таблица 1
Номер кривой Материал E, МПа µ, МПа ν α, МПа β × 105, МН γ × 105, МН ε × 105, МН
1 Полиуретан 300 104 0.40 –8.66 3.00 4.00 –2.00
2 Пенополи-метакриламид 637 285 0.12 –23.75 –30.00 60.00 –10.00
3 Синтети- ческая пена 2758 1033 0.34 –229.55 0.45 0.42 –0.29
Фиг. 3

Сравнение зависимостей перемещения $w$ от координаты $x$ по микрополярной (сплошные кривые) и классической (штриховые кривые) теориям изгиба пластин при следующих значениях параметров:

$h = 0.1\;{\text{м }},\quad a = 1\;{\text{м }},\quad q = 0.1\;{\text{М П а }},\quad {\text{M}} = - 0.25 \times {{10}^{{ - 6}}}\;{\text{М П а /м }}$
представлены на фиг. 3 слева, в случае защемленных краев и справа в случае шарнирно опертой пластины, причем кривые, соответствующие чистому изгибу, снабжены маркером в виде светлой точки. В связи с симметрией кривых относительно оси $x = 0.5$ показана лишь область $0 \leqslant x \leqslant 0.5$.

4. Заключение. Предложенный подход к исследованию задач изгиба пластин существенно упрощает процесс решения. В рассмотренных задачах полученные результаты соответствуют известным решениям [25]. Практические расхождения прогибов по классической и микрополярной теориям изгиба пластин, представленных на фиг. 3, объясняются влиянием моментных напряжений на функцию перемещений.

Предложенный алгоритм решения задач можно будет использовать при проектировании инженерных прикладных программных продуктов.

Список литературы

  1. Nowacki W. Teoria sprężystości. Warszawa: Wyd. Nauk. PWN, 1970. 460 p. = Новацкий В. Теория упругости. М.: Изд-во Мир, 1975. 872 с.

  2. Nowacki W. Three-dimensional problem of micropolar theory of elasticity // Bull. Acad. Polon. Sci. Ser. Sci. Techn. 1974. V. XXII. № 5. P. 225–233.

  3. Kirchhoff G. Vorlesungen über mathematische Physik. Mechanik. Leipzig. 1876. 486 p. = Кирхгоф Г. Механика. Лекции по математической физике. M.: Изд-во АН СССР, 1962. 402 с.

  4. Kirchhoff G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe // ZAMM. 1850. Bd 40. № 1. S. 51–88.

  5. Mindlin R. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates // Appl. Mech. 1951. V. 18. № 1. P. 31–38.

  6. Reissner E. The effect of transverse shear deformation on the bending of elastic plates // Trans. ASME J. Ser. E. Appl. Mech. 1945. V. 12. P. 68–77.

  7. Амбарцумян С.А. Теория анизотропных пластин. Прочность. Устойчивость и колебания. М.: Наука, 1967. 266 с.

  8. Зубов Л.М., Еремеев В.А. Механика упругих микрополярных оболочек // Дальневост. мат. ж. 2003. Т. 4. № 2. С. 182–225.

  9. Зубов Л.М. Универсальные решения для изотропных несжимаемых микрополярных тел // Докл. АН. 2010. Т. 435. № 1. С. 35–39.

  10. Левин В.А. Равновесие микрополярных тел с предварительно деформированными областями. Наложение больших деформаций // ПММ. 2017. Т. 81. Вып. 3. С. 330–336.

  11. Геворкян Г.А. Модифицированный метод конечных элементов в механике деформируемых твердых тел // Ереван. Изд-во ЕГУАС, 2013. 392 с.

  12. Геворкян Г.А., Варданян С.В., Пирумян Н.В., Мехрабекян Н.Р. Об одной модификации уравнений поперечного изгиба пластин с учетом моментных напряжений // Сб. научн. тр. ЕГУАС. 2013. Т. IV (51). С. 101–107.

  13. Геворгян Г.А., Варданян С.В., Пирумян Н.В., Мехрабекян Н.Р. Метод конечных элементов прямоугольных форм для решения задач поперечного изгиба пластин с учетом моментных напряжений // Сб. научн. тр. ЕГУАС. 2014. Т. I (52). С. 52–66.

  14. Геворгян Г.А., Варданян С.В., Пирумян Н.В., Мехрабекян Н.Р. Об одной модификации метода конечных элементов прямоугольных форм для решения задач поперечного изгиба пластин с учетом моментных напряжений // Сб. научн. тр. ЕГУАС. 2015. Т. III (58). С. 51–65.

  15. Wrobel L.C., Aliabadi M.H. The Boundary Element Method. V. 1, 2. Chichester: Wiley, 2002. 1066 p.

  16. Huang S., Liu Y.J. A fast multipole boundary element method for solving the thin plate bending problem // Engng Anal. Bound. Elements. 2013. № 37. P. 967–976.

  17. Amabili M. Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments // Comput. Struct. Nonlin. Dynam. Contin. Syst. 2004. V. 82. Iss. 31–32. P. 2587–2605.

  18. Cowin S.C. An incorrect inequality in micropolar elasticity theory // ZAMP. 1970. Bd 3. V. 21. S. 494–497.

  19. Cowin S.C. Stress functions for cosserat elasticity // Int. J. Solids Struct. 1970. V. 6. Iss. 4. P. 389–398.

  20. Lakes R.S. Experimental micro mechanics methods for conventional and negative Poisson’s ratio cellular solids as Cosserat continua // J. Engng Mater. Techn. 1991. V. 113. Iss. 001. P. 148–155.

  21. Farshad M., Wildenberg M.W., Flüeler P. Determination of shear modulus and Poisson’s ratio of polymers and foams by the antielastic plate-bending method // Mater. Struct. 1997. V. 30. Iss. 6. P. 377–382.

  22. Lakes R.S. Physical meaning of elastic constants in Cosserat, void, and microstretch elasticity // Mech. Mater. Struct. 2016. V. 11. № 3. P. 217–229.

  23. Зезин Ю.П., Ломакин Е.В., Мамонов С.В. и др. Определение модуля упругости покрытий по результатам испытаний на растяжение и изгиб трехслойных образцов // Зав. лаб. диагн. матер. 2012. Т. 78. № 8. С. 61–63.

  24. Зезин Ю.П., Ломакин Е.В., Мамонов С.В. и др. Определение упругих характеристик полимерных покрытий по результатам испытаний на растяжение и изгиб плоских образцов // Изв. Саратовск. ун-та. Новая серия. Сер. Матем. Механ. Информ. 2012. Т. 12. № 3. С. 66–72.

  25. Амбарцумян С.А. Микрополярная теория оболочек и пластин. Ереван: Изд-во Гитутюн НАН РА, 2013. 223 с.

  26. Амбарцумян С.А. Теория поперечного изгиба пластин по несимметричной теории упругости // Механ. композ. матер. 1996. Т. 32. № 1. С. 42–52.

  27. Амбарцумян С.А. Теория изгиба пластин на основе уравнений несимметричной упругости // Изв. РАН. МТТ. 1997. № 1. С. 152–164.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал