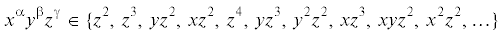Прикладная математика и механика, 2019, T. 83, № 1, стр. 84-94

В практике инженерных расчетов напряженно-деформированное состояния (НДС) упругих тел в аналитической форме учет объемных сил детально разработан лишь для консервативных (потенциальных) сил. Это связано с использованием общего решения Папковича–Нейбера [1], обусловленного учетом таких сил, и по причине того, что в традиционных исследованиях трудно встретить объемные силы непотенциального характера. Имеются классические примеры решения задач с потенциальными силами [2]. Общее решение в перемещениях выражается через тензор Грина и может быть получено лишь численно, что ограничивает возможность его применения. Расширение числа вариантов исследуемых объектов приводит к ситуации, когда объемные силы порождаются не традиционными механическими причинами (гравитация, инерция), а причинами иного физического характера (например, взаимодействием тел с электромагнитным полем). Такое возможно, поскольку тело может быть однородным в механическом отношении, но обладать неоднородными электромагнитными свойствами и, соответственно, испытывать действия сил из классов более широких, чем консервативные.

Необходимость решения задач с непотенциальными объемными силами возникает при рассмотрении проблем, связанных с деформациями механически неоднородных тел. Разложение параметров состояния в ряд по малому безразмерному параметру приводит к появлению фиктивных объемных сил, которые не являются потенциальными. Фиктивными силами называем выражения, которые находятся на месте реальных объемных сил, в уравнениях равновесия. Их приближение потенциальными силами иногда оказывается допустимым способом решения [3], но не всегда эффективным.

Разработка надежного общего подхода, позволяющего эффективно справляться с трудностями, возникающими из-за неконсервативности объемных сил, является конечной целью представленной работы. Удачная попытка в плане приложения, но без доказательства существования базиса внутренних состояний от полиномиальных сил, делалась ранее [4, 5]. Эффективность нового подхода подкреплена решением смешанных задач для односвязных ограниченных тел: о равновесии усеченного конуса под воздействием неконсервативных объемных сил и о равновесии неоднородного тяжелого упругого полушара (здесь эффект возникновения фиктивных объемных сил проявляется на каждом шаге итерации метода возмущений).

1. Обоснование метода построения напряженно-деформированного состояния. Традиционно объемные силы в задачах теории упругости учитывались в консервативной форме, что позволяло на базе фундаментальных решений Папковича–Нейбера установить соответствующее поле перемещений [1].

Поле перемещений выражается через решение уравнения Пуассона

следующим образом:

Здесь $\nu $ – коэффициент Пуассона, $\mu $ – модуль сдвига, $\Pi $ – потенциал объемных сил. Поле перемещений позволяет восстановить все параметры внутреннего состояния из соотношений теории упругости Коши

и обобщенного закона Гука а также объемные силы из уравнений равновесия где ${{\varepsilon }_{{ij}}}$ и ${{\sigma }_{{ij}}}$ – компоненты тензоров деформаций и напряжений, ${{\delta }_{{jk}}}$ – символ Кронекера, $\lambda $ – параметр Ламе. Через ${{\tilde {u}}_{i}}$ выражаем соответствующие поля деформаций и напряжений ${{\tilde {\varepsilon }}_{{ij}}}$, ${{\tilde {\sigma }}_{{ij}}}$. Набор $\tilde {\xi } = \{ {{\tilde {u}}_{i}},{{\tilde {\varepsilon }}_{{ij}}},{{\tilde {\sigma }}_{{ij}}}\} $ соответствует внутреннему состоянию тела, вызванному только объемными силами. Знание этого состояния позволяет разделить решение задачи на две части: $\xi = \xi ^\circ + \tilde {\xi }$, где $\xi $ – искомое внутреннее состояние, $\xi ^\circ $ – состояние, обусловленное граничными условиями, учитывающими их изменение вследствие действия объемных сил на границе.

Использование вышеизложенной процедуры проблематично в случае неконсервативных объемных сил. Предлагается иной подход. Считаем поле перемещений в сплошном теле описанным многочленами от $x,y$, z. Моном $w = {{x}^{\alpha }}{{y}^{\beta }}{{z}^{\gamma }}$ можно назначить в качестве любой компоненты вектора перемещения ${\mathbf{u}}(x,y,z)$, образуя некоторое допустимое упругое состояние. Например, в случае ${\mathbf{u}} = \{ w,0,0\} $ по формулам (1.1) и (1.2) определяем соответствующие тензоры деформаций и напряжений

Из уравнений равновесия (1.3) получаем выражение для вектора объемной силы

обеспечивающее замыкание определяющих соотношений.

Варьируя целые α, β, γ, можно предложить множество таких состояний. Перебирая всевозможные варианты в пределах $\alpha + \beta + \gamma \leqslant n$, получаем множество векторов объемных сил, компоненты которых образованы однородными многочленами до порядка $n - 2$ включительно. Принципиальным является вопрос: содержит ли это множество конечномерный базис, позволяющий разложить произвольный вектор объемных сил в ряд Фурье по его элементам при увеличении числа n до бесконечности?

Следующие наводящие соображения позволяют понять логику дальнейших действий. Во-первых, анализ достаточно провести для фиксированного множества $n = \alpha $ + + β + γ и установить возможность построения базиса внутри этого множества. Во-вторых, достаточно проанализировать лишь одну из компонент вектора ${\mathbf{X}}$ (выводы по отношению к другим компонентам обусловлены циклической симметрией). В-третьих, если система компонент, назначенных в соответствии с верхним элементом столбца (1.4), будет линейно независимой, то таковой станет и система векторов объемных сил. В-четвертых, применение разработанного авторами алгоритма построения базиса для $n = 2,3, \ldots ,12$ подтвердило теоретически возможное число $m$ линейно независимых многочленов от номера $n$.

Отметим, что во множестве элементов базиса, характеризующихся максимальным порядком многочлена $n$, содержится $(n - 1)n{\text{/}}2$ линейно-независимых многочленов, что равно комбинаторному числу линейно независимых мономов порядка $n - 2$. Следовательно, базис многочленов, аппроксимирующий произвольный многочлен порядка $n - 2$, полный. Разработан алгоритм формирования базиса из многочленов до десятого порядка включительно. Число линейно независимых векторов, составленных по этой схеме, равно $\frac{3}{2}\sum\nolimits_{i = 1}^{n - 1} {i(i + 1)} $. Таким образом, существует базис пространства полиномиальных объемных сил во множестве вариантов, порождаемых указанным приемом.

При расчетах полезно знать набор мономов ${{x}^{\alpha }}{{y}^{\beta }}{{z}^{\gamma }}$, порождающих линейно независимые элементы базиса пространства полиномиальных объемных сил. Ниже приведен отрезок до четвертого порядка включительно

Наличие базиса позволяет провести его ортогонализацию и нормирование в соответствии со скалярным произведением, выражаемым интегралом от скалярного произведения векторов в алгебраическом смысле

Любой вектор объемных сил может быть представлен в виде ряда Фурье

где ${\mathbf{X}}_{{{\text{ort}}}}^{{(k)}}$ – $k$-я объемная сила из ортонормированного базиса. Поскольку объемная сила X известна, можно оценить ошибку аппроксимации при замене бесконечного ряда конечной суммой $n$ слагаемых из левой части неравенства Бесселя:

Величина δ используется для выбора числа членов ряда, обеспечивающих заранее оговоренную точность аппроксимации объемных сил.

Каждому базисному вектору ${{{\mathbf{X}}}^{{\left( k \right)}}}$ соответствуют вектор перемещения ${{{\mathbf{\tilde {u}}}}^{{\left( k \right)}}}$ и тензоры деформаций ${{\tilde {\hat {\varepsilon }}}^{{(k)}}}$ и напряжений ${{\tilde {\hat {\sigma }}}^{{\left( k \right)}}}$, образующие внутреннее НДС ${{\tilde {\xi }}^{{(k)}}} = \{ {{{\mathbf{\tilde {u}}}}^{{(k)}}},{{\tilde {\hat {\varepsilon }}}^{{(k)}}},{{\tilde {\hat {\sigma }}}^{{(k)}}}\} $. Любой линейной комбинации ${{{\mathbf{X}}}^{{\left( k \right)}}}$ соответствует такая же комбинация состояний ${{\tilde {\xi }}^{{(k)}}}$.

Таким образом, после аппроксимации объемной силы рядом можно построить линейную комбинацию элементов ортонормированного базиса пространства $\Xi $ внутренних состояний среды, определяющую НДС $\tilde {\xi }$, обусловленное объемной силой ${\mathbf{X}}$.

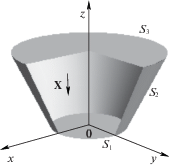
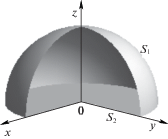
2. Основная смешанная задача о равновесии усеченного конуса под действием неконсервативных объемных сил. Усеченный круговой конус высотой $R$, защемленный по меньшему основанию ${{S}_{1}}$ радиуса $R{\text{/}}2$, свободный от нагружения по большему основанию ${{S}_{3}}$ радиуса $R$ и боковой поверхности ${{S}_{2}}$, находится в равновесии под действием неконсервативных объемных сил, направленных противоположно оси $z$ (фиг. 1):

Материал конуса изотропно упругий с коэффициентом Пуассона $\nu = 0.25$, параметры Ламе $\lambda = \mu = 1$ представлены в безразмерной форме. Линейный характерный размер принят равным $R$.

Ортогонализация начальных элементов базиса проводилась исходя из скалярного произведения (1.5), строилась матрица Грама $G = [({{{\mathbf{X}}}^{{(i)}}},{{{\mathbf{X}}}^{{(j)}}})]$ с дальнейшим ее разложением по Холецкому. Это возможно из-за того что матрица Шмидта (левый множитель $H$, переводящий исходный базис в ортонормированный) совпадает с обратной матрицей, участвующей в разложении Холецкого.

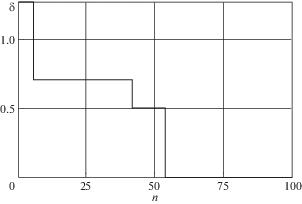
Ошибка ортогонализации оценивалась по квадратичной норме матрицы $\left\| {HG{{H}^{T}} - E} \right\|$ ($E$ – единичная матрица) и составила малую величину порядка ${{10}^{{ - 10}}}$. Разложение заданной в задаче объемной силы по ортонормированному базису оценивалось в соответствии с определением (1.7), и его погрешность составила малую величину $\delta = 3 \times {{10}^{{ - 7}}}$, обусловленную лишь вычислениями. Зависимость $\delta $ от числа $n$ элементов базиса приведена на фиг. 2.

Характер изменения погрешности свидетельствует о высокой точности аппроксимации объемной силы базисом из 58 элементов, принадлежащих множеству, характеризуемому максимальным порядком мономов $n = 3$. Линейная комбинация элементов ортонормированного базиса пространства внутренних состояний с коэффициентами Фурье позволила установить внутреннее состояние, отвечающее заданной объемной силе. После округления коэффициентов до рациональных значений состояние, удовлетворяющее определяющим соотношениям (1.1)–(1.3), получено точно (проверяется непосредственной подстановкой ${\mathbf{\tilde {u}}}$, $\tilde {\hat {\varepsilon }}$, $\tilde {\hat {\sigma }}$ в равенства (1.1)–(1.3)):

Упругое поле $\tilde {\xi }$ позволяет сформировать поправку в граничные условия, учитывающую влияние объемных сил ${\mathbf{X}}$, для определения состояния $\xi ^\circ $. В полярных координатах $r$, $\varphi $ граничные условия принимают вид

Решение краевой задачи проводилось методом граничных состояний [6]. Для определения коэффициентов Фурье в смешанной задаче формировалась бесконечная система уравнений

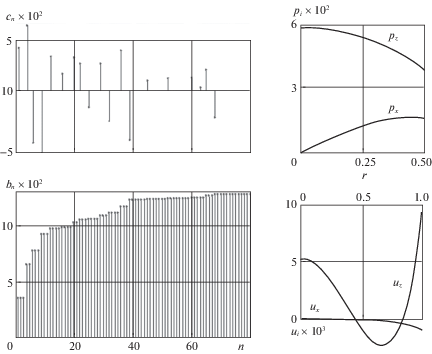
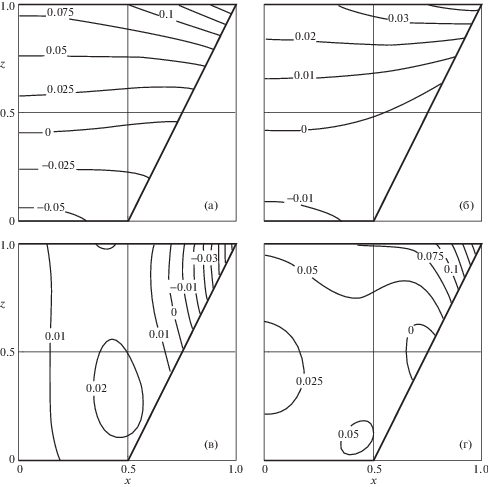
Расчеты проводились для 80 элементов базиса. Значения коэффициентов Фурье приведены в графической форме в левой верхней части фиг. 3. В левой нижней части представлен характер насыщения суммы Бесселя $b$ (см. вторую формулу (1.7)) в зависимости от числа элементов $n$, косвенно свидетельствующий о сходимости решения. Поскольку определяющие соотношения среды удовлетворены тождественно, о точности решения можно судить по величине среднеквадратичной интегральной невязки заданных граничных условий и построенного граничного состояния. Она составила 0.017 в безразмерной форме. Результирующее состояние – суперпозиция состояний, обусловленных действием объемной силы и влиянием граничных условий.

В нижней части фиг. 3 приведены результаты решения задачи в графической форме (эпюры механических величин в осевом сечении $y = 0$ границ, линии уровня напряжений в осевом сечении тела). Распределение осевых усилий (правая верхняя часть фиг. 3) свидетельствует о том, что, несмотря на неоднородность объемных сил в любом сечении $z = {\text{const}}$, наибольшая осевая реакция возникает на оси симметрии; она убывает по мере приближения к границе основания. Радиальные составляющие реакции равны нулю на оси симметрии и возрастают по мере приближения к границе, достигая своего максимума в точке, близкой к границе. Изменение формы свободной поверхности конуса (правая нижняя часть фиг. 3) характеризуется незначительным радиальным смещением ее в сторону центра основания, увеличивающимся по модулю по мере приближения к границе основания и достаточно сложной формой изменения поверхности основания. Он обусловлен осевыми смещениями: незначительный провал наблюдается за пределами полурадиуса основания и захватывает кольцо $r \in (0.45,0.88)$, внутри которого и значительно больше снаружи поверхность основания выпучивается вверх. Этот эффект неочевиден.

На фиг. 4 приведены линии уровня напряжений в осевом сечении $y = 0$ тела. Осевые напряжения ${{\sigma }_{{zz}}}$ (фиг. 4, а) – сжимающие в нижней части тела и растягивающие ближе к верхнему основанию, причем растяжения осевых волокон усиливаются по мере приближения к боковой границе конуса, достигая максимума на границе с верхним основанием. С такими осевыми напряжениями согласуется распределение радиальных напряжений ${{\sigma }_{{xx}}}$ (б), которые также сжимающие в нижней части тела и растягивающие в верхней. Окружные напряжения по характеру мало отличаются от радиальных, поэтому здесь не приведены. Напряжения сдвига ${{\sigma }_{{xz}}}$ (в), отвечающие за изменения формы, сконцентрированы на верхнем круговом ребре, имеют положительный характер в основной массе тела $r < 0.65$, достигая максимума на окружности радиуса 0.45, отстоящей от нижнего основания на высоту 1/3. Картина линий уровня наибольших касательных напряжений (г) свидетельствует о том, что наиболее опасной зоной возникновения условий разрушения является верхнее круговое ребро тела. Напротив, зоны, примыкающие к оси симметрии и боковой границе тела примерно на уровне $z = 0.5$, стабильны по отношению к возможности разрушения.

3. Равновесие поверхностно упрочненного тяжелого полушара. Тяжелый полушар безразмерного радиуса $R = 1$ сцеплен экваториальным сечением с горизонтальным жестким основанием (фиг. 5) и находится в равновесии под действием силы тяжести безразмерной интенсивности 1. При фиксированном коэффициенте Пуассона $\nu = 0.25$ материал шара неоднородный: по мере приближения к сферической границе модуль упругости возрастает в соответствии с зависимостью λ = μ = 1 + β(x² + y² + z²) (в центр полушара помещено начало системы координат $Oxyz$; $z$ – ось симметрии).

Систематическое исследование неоднородных упругих сред проведено В.А. Ломакиным [7]. Здесь, в частности, установлен эффект присутствия объемных сил, порожденный процедурами разложения в асимптотические ряды.

Проведем разложение определяющих соотношений среды методом Пуанкаре, полагая $\beta $ малым параметром. Представим искомое состояние в форме асимптотического разложения

Считая граничные условия отнесенными к состоянию ${{\xi }^{0}}$, получаем последовательность задач изотропной теории упругости в безразмерном виде

где $s_{{i\,j}}^{m}$ выполняет роль компоненты тензора напряжений и находится по решении задачи $m$ приближения. Тензор напряжений восстанавливается по правилу

Из выражения (3.1) следует, что при решении неоднородной задачи появляется эффект наличия неконсервативных объемных сил на каждом шаге приближения. Решение для каждого фиксированного $m$ проводится в соответствии с процедурами, описанными в разд. 2, причем при этом в нулевом приближении $m = 0$ поправленные граничные условия должны быть полностью выполнены. Отсюда ясно, что при высших приближениях для их решения достаточно рассматривать задачи только одного типа, к примеру задачу в перемещениях.

Эффективным средством решения задачи на каждом шаге итерации является метод граничных состояний (МГС), предоставляющий результаты решения в символьном виде. Технические достоинства метода следующие: 1) ортонормированный базис пространства $\Xi $ строится однократно для тела определенной формы и может далее использоваться при решении различных краевых задач; 2) матрица коэффициентов бесконечной системы уравнений (БСУ) строится однократно, поскольку изменение параметров нагружения влияет лишь на правые части БСУ; 3) решение основных задач (матрица коэффициентов БСУ – единичная) сводится к громоздкому вычислению квадратур; 4) в итерационном процессе при $m > 0$ МГС позволяет далее не рассматривать смешанную задачу, а использовать какую-либо основную задачу, формулируя граничные условия соответствующим образом, например, ${{\left. {\mathbf{p}} \right|}_{{\partial V}}} = 0$ для первой основной задачи, ${{\left. {\mathbf{u}} \right|}_{{\partial V}}} = 0$ для второй основной задачи.

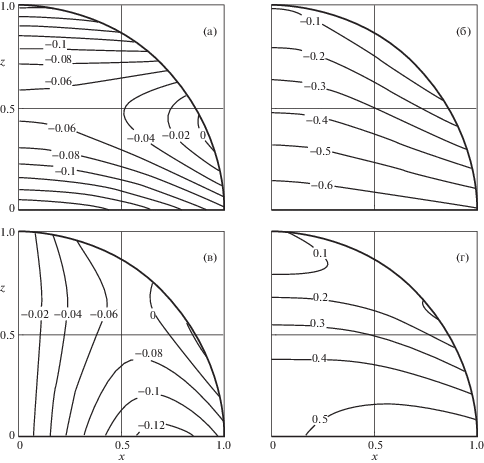
Вычисления проводились при $\beta = 0.1$. Были выполнены приближения до $m = \,\,2$ и построены результирующие поля, отвечающие за НДС, имеющие форму громоздких аналитических выражений. На фиг. 6 представлены изолинии напряжений, построенные в сечении $y = 0$ полушара:

а) радиальное напряжение ${{\sigma }_{{xx}}}$, б) осевое напряжение ${{\sigma }_{{zz}}}$, в) напряжение сдвига ${{\sigma }_{{xz}}}$, г) наибольшие касательные напряжения.

Анализ поля радиальных напряжений ${{\sigma }_{{xx}}}$ в сечении $y = 0$ свидетельствует о том, что радиальные волокна внутри полушара всюду сжимаются, причем наибольшие значения напряжения сжатия принадлежат как полярной шапке полушара, так и зоне, примыкающей к оси шара на экваторе. У поверхности шара в районе широт $\theta = 30^\circ $ радиальные волокна сжимаются слабо. Осевые напряжения также всюду сжимающие, причем в области экватора характер сжатия осевых и радиальных волокон примерно одинаков, а на поверхности шара наименьшие сжатия испытывают осевые волокна на широте $\theta = 60^\circ $. Наибольший сдвиг наблюдается в окрестности экватора в кольце, примыкающем к радиусу $r = 0.7$. Анализ наибольших касательных напряжений свидетельствует о том, что зона, примыкающая к оси вблизи полюса, деформирована слабо, а разрушение следует ожидать в экваториальном сечении примерно на уровне $r = 0.7$.

4. Выводы.

1. Предложен и обоснован эффективный обратный способ оценки с высокой точностью НДС упругого тела, обусловленного объемными силами, позволяющий восстанавливать поля напряжений и деформаций от распределенных сил из класса приближаемых полиномами.

2. Для НДС от полиномиальных объемных сил возможно построение строгого решения.

3. Способ применен для решения задачи о равновесии усеченного кругового конуса, жестко сцепленного по меньшему основанию с жесткой подложкой, находящейся под воздействием неоднородных объемных сил гравитационного типа. НДС, вызванное действиями объемных сил, получено строго.

4. Способ явился эффективным аппаратом решения неоднородных задач теории упругости, поскольку при разложении по малому параметру на каждом шаге возникает эффект наличия непотенциальных объемных сил. Решена задача о равновесии поверхностно упрочненного тяжелого полушара.

5. Сочетание методов Пуанкаре и граничных состояний выявило еще одно преимущество МГС по сравнению с иными подходами, а именно, на всех итерациях, следующих за нулевой, нет необходимости решать краевую задачу в смешанной постановке; достаточно рассматривать вариант какой-нибудь основной задачи. Это обусловлено тем, что граничное состояние содержит всю информацию, по которой можно формулировать задачи совершенно различные по типу и при этом равноценные по результатам решения.

6. К преимуществам способа следует отнести тот факт, что при любом порядке базиса полученное состояние является решением системы дифференциальных уравнений равновесия. Такие решения могут служить в качестве поверочных для решений, полученных, к примеру, методом конечных элементов.

Использование компьютерной алгебры и обратный переход к размерным величинам принципиально позволяют выписывать решение в форме пусть громоздких, но приближенных полнопараметрических аналитических выражений [8].