Прикладная математика и механика, 2019, T. 83, № 1, стр. 95-106

1. Введение. Построение новых определяющих соотношений (ОС) вязкоупругих сред при конечных деформациях проводится ниже с применением метода, использованного ранее для упругопластических тел и тел с памятью формы [1, 2]. Суть метода состоит в подстановке новых пар тензорных мер напряжений и конечных деформаций в выбранные формы определяющих соотношений, например, применяемые при малых деформациях. В качестве таких мер, в частности, могут быть использованы “индифферентные” тензоры (другие названия – “пространственно ориентированные”, или “левые”), т.е. преобразующиеся при замене системы отсчета к тензорам ${{\hat {Z}}_{*}}(t)$ по формуле

где $\hat {Z}(t)$ – индифферентный тензор в исходной системе отсчета, $\hat {\theta }(t)$ – ортогональный тензор перехода к новой системе отсчета. В этом случае производные по времени D[$\hat {Z}$], входящие в ОС, должны быть определены так, чтобы получающийся тензор D[$\hat {Z}$] также являлся индифферентным. Производные, сохраняющие тип тензора, называются объективными.

Такой подход к построению ОС обеспечивает корректное удовлетворение принципа материальной независимости от системы отсчета. Дополнительную возможность при использовании указанного метода построения ОС дает модификация объективных производных введением скалярных параметров, которые могут быть связаны с температурой, влажностью и т.п. Примененное здесь семейство ОС вязкоупругих сред построено на основе однопараметрического семейства объективных производных Гордона–Шоуолтера.

В соответствии с описанным выше методом выберем в качестве формы ОС вязкоупругих сред дифференциальную форму элементарной модели Максвелла [3]

и обобщим ее, используя тензоры напряжений Коши $\hat {S}$ и скорости деформации $\hat {V}$, а также – однопараметрическое семейство объективных производных Гордона–Шоуолтера ${{D}_{a}}[\hat {S}]$ [4]

Здесь $a \in [ - 1,1]$ – скалярный параметр, $\hat {V} = (\hat {D} + {{\hat {D}}^{T}}){\text{/2}}$ – тензор скорости деформации, $\hat {\Omega } = (\hat {D} - {{\hat {D}}^{T}}){\text{/2}}$ – тензор вихря, $\hat {D} = {{\hat {A}}^{ \bullet }}{{\hat {A}}^{{ - 1}}}$ – тензор градиента скорости, $\hat {A}$ – аффинор деформации. В результате получим следующее ОС:

При a = 1, –1, 0 из выражения (1.2) получаются объективные производные Олдройда, Коттер–Ривлина и Яуманна соответственно [5, 6], а соотношения (1.3) превращаются в ОС вязкоупругих материалов, называемые в англоязычной литературе UCM (upper-convected Maxwell) [7], LCM (lower-convected Maxwell), COM (corotational Maxwell). Выражение (1.2) – частный случай трехпараметрического представления производных конвективно-коротационного типа, предложенного Г.Л. Бровко [8].

Заметим, что ОС (1.2) и (1.3) могут быть записаны с использованием производной Яуманна ${{D}_{J}}[\hat {S}]$ в виде

или в виде равенства содержащего тензор четвертого ранга $\hat {\hat {L}}$обладающий симметрией по первой и второй парам индексов и внутри этих пар. Здесь $\hat {\hat {I}}$ – единичный тензор четвертого ранга. С помощью операций тензорного умножения и транспонирования он может быть представлен через единичный тензор второго ранга $\hat {I}$, например, в виде $\hat {\hat {I}}$ = ${{T}_{{(1,3,2,4)}}}(\hat {I} \otimes \hat {I})$; ${{T}_{\sigma }}$ – операция транспонирования тензоров, $\sigma $ – перестановка упорядоченного набора чисел (1, 2, 3, 4) [9]. В литературе используется также другое обозначение операции, определяющей тензор $\hat {\hat {I}}$ [10]: $\hat {\hat {I}}$ = = ${{(\hat {I} \otimes \hat {I})}^{{(1324)}}}$. В таком случае правая часть этого равенства называется изомером соответствующего вида. При $T \to \infty $ выражение (1.4) превращается в ОС анизотропной гипоупругой среды с тензором упругих модулей $\hat {\hat {L}}$, зависящим от E, a и $\hat {S}$.

Соотношения (1.2) и (1.3) или эквивалентные им соотношения (1.4) содержат дополнительный параметр $a$ по сравнению с упомянутыми моделями типа UCM, что расширяет возможность описания свойств вязкоупругих материалов.

2. Определяющее соотношение для несжимаемого вязкоупругого материала. В дальнейшем будем полагать вязкоупругий материал несжимаемым. В этом случае тензор напряжений Коши определяется с точностью до неопределенного шарового тензора $ - p\hat {I}$ и может быть представлен в виде

$\hat {S}$ – тензор “определяющих напряжений” [11], находится из уравнения (1.4) или из эквивалентного уравнения (1.3). Заметим, что в общем случае $\hat {S}$ не является девиатором тензора $\hat {\sigma }$.

3. Задача о кручении сплошного вязкоупругого цилиндра. Кинематика движения сплошного несжимаемого цилиндра при кручении без удлинения в цилиндрической системе координат задается соотношениями

где R, Ф, Z – цилиндрические координаты точки в начальный момент времени, r, $\varphi $, z – текущие цилиндрические координаты, κ(t) – крутка. Выберем цилиндрические координаты точек тела в начальной конфигурации R, Ф, Z в качестве лагранжевых координат. В этом случае аффинор деформации может быть представлен в виде [12]

Здесь ${\mathbf{e}}_{0}^{r}$, ${\mathbf{e}}_{0}^{\varphi }$, ${\mathbf{e}}_{0}^{z}$ – векторы взаимного базиса лагранжевой системы координат в начальной конфигурации, e_r, e_φ, e_z – векторы естественного лагранжева базиса в текущей конфигурации. Поскольку $\left| {{\mathbf{e}}_{0}^{\varphi }} \right|$ = R^–1 и, в силу закона движения (3.1), |e_φ| = R, в равенстве (3.2) векторы e_φ и ${\mathbf{e}}_{0}^{\varphi }$ можно заменить ортами ${\mathbf{e}}_{\varphi }^{'}$ и ${\mathbf{e}}_{0}^{{'\varphi }}$:

При повороте поперечного сечения цилиндра на угол α векторы e_r и ${\mathbf{e}}_{\varphi }^{'}$ выражаются через e_0r и ${\mathbf{e}}_{{0\varphi }}^{'}$ соотношениями

Для вычисления вектора ${{\bar {e}}_{z}}$ воспользуемся равенством e_z = $\partial {\mathbf{x}}{\text{/}}\partial Z$, где x – радиус-вектор точки цилиндра в текущей конфигурации, причем вследствие закона движения (3.1) x = Re_r + Ze_0z. На основании равенств (3.4) имеем $\partial {{{\mathbf{e}}}_{r}}{\text{/}}\partial Z$ = $k{\mathbf{e}}_{\varphi }^{'}$ и, следовательно,

Подставляя выражения (3.4) и (3.5) в соотношение (3.3) и учитывая, что

получим выражение для аффинора деформации в виде

Таким образом, в диадном базисе, построенном на векторах e_0r, ${\mathbf{e}}_{{0\varphi }}^{'}$, e_0z, матрица аффинора деформации имеет вид

Найденные ниже компоненты тензора напряжений также относятся к упомянутому базису.

Учитывая, что напряженно-деформированное состояние остается неизменным по длине цилиндра, будем рассматривать сечение Z = 0. Для него $\alpha (t) = 0$, и аффинор и введенные выше матрицы принимают вид

Подставляя полученные матрицы в ОС (1.2), (1.3) и (2.1), получим систему линейных дифференциальных уравнений относительно компонент тензора $\hat {S}$. Полагая далее κ(t) = $\text{v}t$, $\text{v}$ = const, будем иметь

Здесь координаты R, φ, Z занумерованы в порядке 1, 2, 3; точкой над компонентами тензора $\hat {S}$ обозначена производная по безразмерному параметру $\tau : = t{\text{/}}T$, а также введены безразмерные параметры $\rho : = R{\text{/}}{{R}_{0}}$ и $L: = {{R}_{0}}Tv$. Будем считать, что $\hat {\sigma }$(0) = 0, p(0) = 0. В таком случае $\hat {S}(0) = \hat {0}$, и решение системы (3.6) имеет вид

(для любого $a$), остальные безразмерные компоненты $\hat {S}{\text{/}}E$ представлены в таблице 1 (для произвольного значения $a$ и в частных случаях $a = \pm 1,0$).

Здесь использованы следующие обозначения:

Значения ${{S}_{{22}}}{\text{/}}E$ при $a = 1$ и ${{S}_{{33}}}{\text{/}}E$ при $a = - 1$ получаются из выражений, приведенных во второй строке таблицы 1, соответствующими предельными переходами или непосредственным решением системы (3.6) при указанных значениях параметра а.

Неизвестный аддитивный шаровой тензор $ - p(\rho ,\tau )\hat {I}$, с точностью до которого соотношением (2.1) определяется тензор напряжений Коши для несжимаемого материала, в рассматриваемой задаче находится из уравнения равновесия цилиндра в проекции на ось R

при граничном условии ${{\left. {({{S}_{{11}}} - p)} \right|}_{{\rho = 1}}} = 0$. Учитывая, что ${{S}_{{11}}} \equiv 0$, получим

Найденное ненулевое значение аддитивного тензора $ - p(\rho ,\tau )\hat {I}$ отличает решение рассматриваемой задачи о кручении цилиндра от решения аналогичной задачи о простом сдвиге [13].

Подставляя приведенные в таблице 1 выражения для компонент тензора $\hat {S}$, а также найденную функцию $p(\rho ,\tau )$ в формулу (2.1), найдем тензор напряжения Коши $\hat {\sigma }$ в рассматриваемой задаче. Зная компоненты $\sigma _{{23}}^{{}}(\rho ,\tau )$ и $\sigma _{{33}}^{{}}(\rho ,\tau )$, вычислим продольную силу и крутящий момент, соответствующие рассматриваемой кинематике (3.1)

В частных случаях $a = \pm 1$ интеграл в выражении (3.7) легко вычисляется, в итоге получаются следующие выражения для $p(\rho ,\tau )$ и компонент тензора напряжения Коши:

при $a = 1$

при $a = - 1$

(верхние индексы указывают на объективную производную, соответствующую выбранным значениям параметра $a$: Олдройда или Коттер–Ривлина)_. Подставляя выражения (3.9) и (3.10) в формулы (3.8), получим

При других значениях параметра $a$ интеграл (3.7) находится численно.

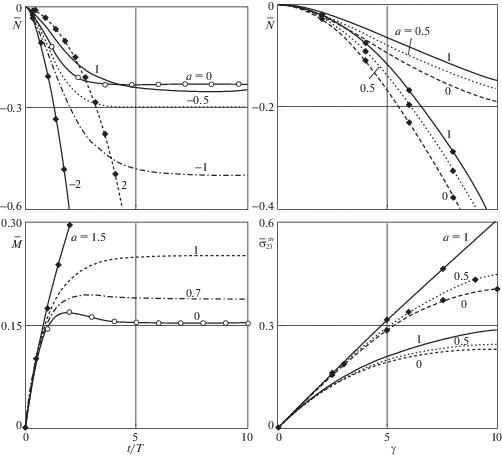
В левой части фиг. 1 приведены графики безразмерных усилий $\bar {N}(\tau )$ = $N(\tau ){\text{/}}(\pi R_{0}^{2}E)$ (верхняя часть) и моментов $\bar {M}(\tau )$ = $M(\tau ){\text{/}}(\pi R_{0}^{3}E)$ (нижняя часть) при разных значениях параметра a, при которых они были получены; кривыми с маркерами в виде ромбов показаны функции $\bar {N}(\tau )$ и $\bar {M}(\tau )$ при $a \notin [ - 1,1]$.

Заметим, что из формул (3.11) функции $f(\tau )$ и $g(\tau )$ могут быть выражены через осевую силу $N(\tau )$ и момент $M(\tau )$ соответственно, после чего подставлены в соотношения (3.9) или (3.10). В результате получим

где ${{J}_{p}}$ – полярный момент инерции кругового сечения.

4. Ступенчатые процессы деформации.

Одноступенчатый процесс. Приведенное в предыдущем разделе решение задачи о кручении вязкоупругого цилиндра, полученное в предположении, что $\dot {\kappa }$(t) = const, позволяет найти напряжения для кусочно-линейной функции крутки

При $t \in [0,{{t}_{0}}]$ решение определяется формулами из таблицы 1. При $t > {{t}_{0}}$ в системе (3.6) $\dot {\kappa }$(t) = 0 и, используя предположение о непрерывности напряжений при $t = {{t}_{0}}$, в этом случае для ненулевых компонент тензора $\hat {S}$ легко получим

Переход в выражениях (4.1) и (4.2) к пределу при ${{t}_{0}} \to 0$, $v{{t}_{0}} = {{\kappa }_{0}}$ дает решение рассматриваемой задачи о кручении в случае одноступенчатого процесса деформации $\kappa (t) = {{\kappa }_{0}}h(t)$ ($h(t)$ – функция Хевисайда)

Здесь

При этом, согласно формулам (3.7) и (3.8),

Продольная сила $N(t)$ в общем случае не выражается через элементарные функции, но легко может быть найдена численно.

Из приведенных формул следует, что если $\kappa (t)$ имеет одноступенчатый вид (процесс релаксации), то ${{S}_{{\alpha \beta }}}(R,t)$, $p(R,t)$, $N(t)$ и $M(t)$ асимптотически стремятся к нулю при $t \to \infty $, причем полученное решение будет иметь физический смысл, если $S_{{23}}^{0}$, $S_{{22}}^{0}$ и $\left| {S_{{33}}^{0}} \right|$ возрастают с ростом ${{\kappa }_{0}}$ для любого $R$, т.е. при ${{R}_{0}}{{\kappa }_{0}}\sqrt {1 - {{a}^{2}}} $ ≤ $\pi {\text{/}}2$.

В частных случаях $a = \pm 1,0$ из формул (4.4) и (4.5) следует:

при $a = 1$

при $a = - 1$

при $a = 0$

Аналогично можно рассмотреть двухступенчатый процесс деформации с функцией крутки вида

В этом случае при $0 < t \leqslant {{t}_{1}}$ решение задается формулами (4.3), при $t > {{t}_{1}}$ напряжения получаются предельным переходом при

из решения задачи о кручении цилиндра с круткой

В результате при $t > {{t}_{1}}$ будем иметь

Здесь

5. Анализ результатов. 1. Из выражений для тензора $\hat {S}$, приведенных в таблице 1, а также формул (3.7) и (3.8) видно, что ОС (1.3) и (2.1) при любом значении параметра $a$ позволяют описать возникновение продольной силы при кручении вязкоупругого цилиндра неизменной длины, что аналогично эффекту Пойнтинга для упругих материалов [11], причем несложно показать, что $N(t) < 0$ при $t > 0$. При этом зависимости безразмерного продольного усилия $\bar {N}(\tau )$ и безразмерного среднего сдвигового напряжения

от деформации сдвига $\gamma (t) = {{R}_{0}}\kappa (t){\text{/}}2$, приведенные в правой части фиг. 1 при разных значениях параметра а, качественно согласуются (в пределах монотонности функций $N(t)$ и $M(t)$ (анализ монотонности см. ниже)) с экспериментальными данными, полученными при кручении цилиндров неизменной длины из наполненного полимерного материала, имитирующего твердое топливо [14]. Кривые с маркерами в виде ромбов соответствуют скорости изменения крутки в 10 раз большей, чем кривые без маркеров.

2. Согласно формулам (3.11), при $a = \pm 1$ и любых $t > 0$ выполняются неравенства $N(t) < 0$, $M(t) > 0$, т.е. осевая сила – сжимающая, причем эта сила и момент – монотонные функции времени, так как $\dot {g}(t) > 0$, $\dot {f}(t) > 0$.

При произвольных $a \ne \pm 1$, дифференцируя приведенные в таблице 1 выражения, получим

Отсюда следует, что, также как при использовании производной Яуманна при простом сдвиге, ${{\sigma }_{{\alpha \beta }}}(R,t)$ $\left( {\alpha ,\beta = 2,3} \right)$ – немонотонные функции $t$. Условие монотонности по времени всех компонент тензора напряжения для любого фиксированного $R$, а также крутящего момента и продольной силы имеет вид

где $vt = \kappa (t)$ – крутка. При заданном $a$ отсюда можно получить ограничение, которое надо наложить на функцию $\kappa (t)$, а при известном диапазоне изменения $\kappa (t)$ – условие для параметра $a$, при котором рассматриваемые величины изменяются монотонно:

В частности, если ${{a}_{{\text{*}}}} > 1$, условие монотонности выполняется при любом $a$. Возможная немонотонность функции $M(t)$ проиллюстрирована в левой нижней части фиг. 1.

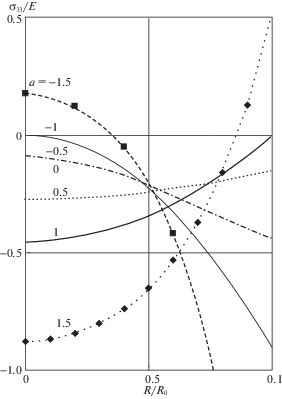
3. На фиг. 2 показаны зависимости ${{\sigma }_{{33}}}{\text{/}}E$ от R при фиксированном t для разных значений а. При любых $a \in [ - 1,1]$ ${{\sigma }_{{33}}}(R) \leqslant 0$. Известен эксперимент Ривлина [15], в котором определяется распределение напряжения ${{\sigma }_{{33}}}$ по радиусу при кручении резинового образца. Вероятно, аналогичный эксперимент для вязкоупругого материала можно использовать для выбора параметра а. Заметим, что при $a \notin [ - 1,1]$ в поперечном сечении цилиндра возникают области растягивающих осевых напряжений (линии с маркерами в виде ромбов на фиг. 2).

4. Для двухступенчатого процесса кручения из формул (4.9) следует, что при

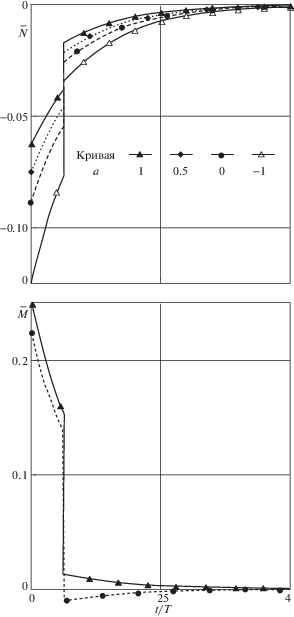
величины $S_{{22}}^{1}$ и $S_{{33}}^{1}$, определяющие скачок $\sigma _{{33}}^{{}}$ и, следовательно, продольной силы $N$ при переходе ко второму этапу, не зависят от длительности первого этапа $t_{1}^{{}}$ (так как выражения в фигурных скобках становятся равными нулю). Отсюда следует, что функции $N(t - {{t}_{1}})$ при $t > {{t}_{1}}$ имеют одинаковый вид при любом ${{t}_{1}}$. Заметим также, что, положив в формулах (4.4) для одноступенчатого процесса кручения ${{\kappa }_{0}} = \kappa _{0}^{'}$, получим при выполнении условия (5.1) следующие равенства: и значит, в рассматриваемом случае нормальное усилие на втором этапе двухступенчатого кручения имеет такой же вид, как и при одноступенчатом процессе. Два отмеченных свойства функции $N(t)$, полученных аналитически в предположении о несжимаемости материала и выполнении ОС (1.3) и (2.1), соответствуют результатам, наблюдавшимся при кручении цилиндров из полиметилметакрилата и полиизобутилена в экспериментах, где длина образцов оставалась неизменной [16].

Виды функций $N(t){\text{/}}E$ для разных значений а при

показаны в верхней части фиг. 3.

5. Из формулы (4.8) следует, что на втором этапе двухступенчатого процесса кручения величина $S_{{23}}^{1}(R)$ может быть как положительной, так и отрицательной в зависимости от значений ${{\kappa }_{0}}$, $\kappa _{0}^{'}$, $a$ и ${{t}_{1}}{\text{/}}T$. Крутящий момент при $t > {{t}_{1}}$ определяется по формуле

и стремится к нулю при $t \to \infty $, убывая от некоторого положительного значения или возрастая от отрицательного в зависимости от знака интеграла в формуле (5.3). Указанные возможности проиллюстрированы в нижней части фиг. 3, где приведены графики безразмерного момента $\bar {M}(t)$ для двухступенчатого процесса кручения при тех же значениях параметров (5.2), что и для графиков в верхней части. Заметим, что на экспериментальных графиках [16] функция $M(t)$ при $t > {{t}_{1}}$ возрастает до некоторого положительного значения, в то время как из формулы (5.3) следует, что $M(t) \to 0$ при $t \to \infty $. Эта особенность решения, полученного для двухступенчатого кручения при использовании ОС (1.3) и (2.1), имеет место также для элементарной модели Максвелла (1.1), на основе которой они построены, и “унаследована” от нее.

6. Заключение. Предложено семейство удовлетворяющих принципу материальной объективности определяющих соотношений вязкоупругих сред при конечных деформациях, обобщающее соотношения элементарной модели Максвелла. Разные элементы семейства формально связаны с однопараметрическим семейством объективных производных Гордона–Шоуолтера. Показано, что эти соотношения могут быть приведены к виду (1.4), содержащему производную Яуманна и тензор четвертого ранга, соответствующий некоторому анизотропному гипоупругому материалу, компоненты которого зависят от параметра а, определяющего конкретную производную из семейства Гордона–Шоуолтера, модуля упругости Е, входящего в исходную модель Максвелла, и тензора напряжений Коши.

Аналитически решена задача о кручении вязкоупругого цилиндра постоянной длины, материал которого описывается произвольным соотношением из указанного семейства. Найденное решение для любого значения параметра а качественно описывает факты, наблюдаемые в экспериментах по кручению вязкоупругих цилиндров неизменной длины: эффект Пойнтинга, зависимость напряженного состояния от скорости деформации, особенности поведения при двухступенчатых нагружениях и релаксации. Для каждого значения параметра а существует область изменения крутки, зависящая от а и радиуса цилиндра, в пределах которой напряжения монотонно меняются со временем. Таким образом, на примере конкретной рассмотренной задачи показана применимость семейства определяющих соотношений (1.3), (2.1) (при любом значении входящего в них параметра а) для описания поведения вязкоупругих материалов с учетом геометрической нелинейности.

Автор благодарит Е.И. Рыжака за доброжелательную, конструктивную критику, полезные замечания и советы, касающиеся содержания работы.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (16-01-00669 А).