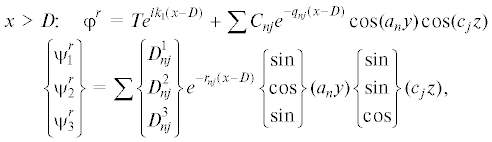1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 1, 2019

Прикладная математика и механика, 2019, T. 83, № 1, стр. 72-83

ПРОСТРАНСТВЕННАЯ ЗАДАЧА О ПРОХОЖДЕНИИ УПРУГОЙ ВОЛНЫ ЧЕРЕЗ ДВА ПАРАЛЛЕЛЬНЫХ ДВОЯКОПЕРИОДИЧЕСКИХ МАССИВА ТРЕЩИН

М. Ю. Ремизов *

Институт математики, механики и компьютерных наук им. И.И. Воровича, Южный федеральный университет
Ростов-на-Дону, Россия

* E-mail: remizov72@mail.ru

Поступила в редакцию 03.10.2017

Полный текст (PDF)

Аннотация

Вычисляются коэффициенты отражения и прохождения в задаче о падении плоской волны на трехмерную систему двух параллельных двоякопериодических массивов трещин. В условиях низкочастотного режима задача сводится к системе интегральных уравнений на одной выделенной трещине. Полуаналитический метод, разработанный ранее для трехмерных скалярных и плоских упругих задач, приводит к явным аналитическим представлениям для волнового поля и параметров рассеяния.

Ключевые слова: коэффициенты отражения и прохождения, двоякопериодическая решетка, гиперсингулярное интегральное уравнение, система трещин, акустический фильтр

1. Введение. Исследование прохождения упругих волн через периодические решетки – важная проблема при ультразвуковом неразрушающем контроле материалов, при изучении распространения звука, а также при использовании электромагнитных волноводов с диафрагмами. Различные численные методы были применены в двумерных задачах с периодическими отверстиями произвольной формы [1–4]. Несмотря на высокую точность компьютерных результатов, существует лишь несколько аналитических теорий. На практике аналитические результаты могут быть получены в случае режима низких частот при слабом взаимодействии волн, когда некоторые приближенные результаты можно установить в аналитической форме. Таким образом, аналитические методы, приводящие к явным формулам для соответствующих параметров рассеяния, справедливы, как правило, только в определенном низкочастотном пределе. Были получены [5–9] аналитические формулы для параметров отражения и прохождения в режиме одной моды для акустических и электромагнитных волн, проникающих сквозь двояко- и троякопериодические массивы отверстий и объемных препятствий произвольной формы. В плоских задачах распространения волн через периодические массивы трещин в упругих твердых телах рассматривались однопериодические [10, 11] и двоякопериодические [12, 13] системы. Все упомянутые источники относятся к скалярной волновой теории.

В настоящей работе продолжается изучение двоякопериодических структур параллельных трещин произвольной конфигурации в трехмерной постановке. Обсуждается пример прямоугольных трещин. Тематика исследования связана с рядом публикаций ([14, 15] и др.), однако здесь применяется другая методика. Как и в некоторых предшествующих работах, принято, что а) распространяется только одна мода при нормальной падающей волне ($a{{k}_{2}}$, $c{{k}_{2}} < \pi $), где ${{k}_{2}}$ – волновое число для поперечной волны, $2a$ и $2c$ – периоды решеток, б) вертикальные плоскости с массивами трещин находятся достаточно далеко друг от друга, так что

(1.1)
$D{\text{/}}a \gg 1,\quad D{\text{/}}c \gg 1,$
где $D$ – расстояние между двумя плоскостями, в которых расположены трещины.

Цель настоящей работы – развитие полуаналитических подходов к вычислению характеристик отражения и прохождения в упругих трехмерных задачах, а также обнаружение ряда новых физических свойств, характерных только для упругих задач, отсутствующих в скалярном случае. Изучаемые проблемы связаны с теорией и практикой использования акустических метаматериалов, которые обладают, благодаря специфической внутренней структуре, свойствами акустических фильтров, т.е. свойствами запирания распространяющейся волны на определенных интервалах частот. Это явление было недавно обнаружено эспериментально [16]. Некоторые фундаментальные аспекты, связанные с акустическими метаматериалами, обсуждаются и в ряде других источников [17–19].

Пространственные задачи акустики в средах (в том числе и упруго-анизотропных) с периодическими системами включений как в длинноволновом приближении, так и в случае более коротких волн, рассматривались и в других работах [20–24].

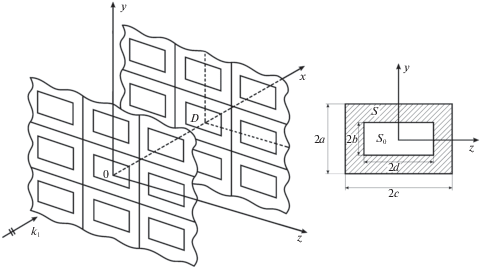
2. Математическая постановка задачи. Рассмотрим трехмерную упругую среду, которая содержит пару параллельных вертикальных двоякопериодических массивов сопараллельных трещин, расположенных при $x = 0$ и $x = D$ соответственно; расстояние $D$ между системами трещин определяет третий период. Период решетки вдоль оси $y$ равен $2a$, вдоль оси $z$ равен $2c$. Будем считать режим колебаний гармоническим по времени с множителем ${{e}^{{ - i\omega t}}}$, который в дальнейшем опускаем. Если изучается падение плоской продольной волны ${{e}^{{i{{k}_{1}}x}}}$ на рассматриваемую решетку вдоль положительного направления оси $x$, то в силу симметрии задача эквивалентна рассмотрению волновода шириной $2a$ вдоль оси $y$ и $2c$ вдоль оси $z$ (фиг. 1). Принимается, что продольная плоская волна в форме

(2.1)
${{\varphi }_{0}} = {{e}^{{i{{k}_{1}}x}}},\quad {{\psi }_{l}} = 0;\quad l = 1,2,3$
приходит из $ - \infty $, порождая рассеянное поле перед первым массивом ($x < 0$), между первым и вторым ($0 < x < D$) и после второго ($x > D$). Тогда потенциалы Ламе, удовлетворяющие уравнению Гельмгольца в соответствующих областях, могут быть представлены в виде тригонометрических рядов Фурье по переменным $y$ и $z$:
(2.2)
$\begin{gathered} x < 0{\text{:}}\quad {{\varphi }^{l}} = {{e}^{{i{{k}_{1}}x}}} + R{{e}^{{ - i{{k}_{1}}x}}} + \sum {{{A}_{{nj}}}{{e}^{{{{q}_{{nj}}}x}}}cos({{a}_{n}}y)cos({{c}_{j}}z)} \\ \left\{ {\begin{array}{*{20}{c}} {\psi _{1}^{l}} \\ {\psi _{2}^{l}} \\ {\psi _{3}^{l}} \end{array}} \right\} = \sum\limits_{} \left\{ {\begin{array}{*{20}{c}} {B_{{nj}}^{1}} \\ {B_{{nj}}^{2}} \\ {B_{{nj}}^{3}} \end{array}} \right\}{{e}^{{{{r}_{{nj}}}x}}}\left\{ {\begin{array}{*{20}{c}} {sin} \\ {\cos } \\ {\sin } \end{array}} \right\}({{a}_{n}}y)\left\{ {\begin{array}{*{20}{c}} {sin} \\ {\sin } \\ {\cos } \end{array}} \right\}({{c}_{j}}z) \\ \end{gathered} $
$0 < x < D{\text{:}}\quad {{\varphi }^{1}} = {{e}^{{i{{k}_{1}}x}}} + F_{0}^{1}cos({{k}_{1}}x) + H_{0}^{1}cos({{k}_{1}}(x - D)) + $
$ + \;\sum {\{ F_{{nj}}^{1}\operatorname{ch} ({{q}_{{nj}}}x) + H_{{nj}}^{1}\operatorname{ch} ({{q}_{{nj}}}(x - D))\} } cos({{a}_{n}}y)cos({{c}_{j}}z)$
(2.3)
$\psi _{1}^{1} = \sum\limits_ \{ G_{{nj}}^{1}\operatorname{ch} ({{r}_{{nj}}}x) + P_{{nj}}^{1}{\text{ch}}({{r}_{{nj}}}(x - D))\} sin({{a}_{n}}y)sin({{c}_{j}}z)$
$\psi _{2}^{1} = \sum\limits_ \{ V_{{nj}}^{1}\operatorname{sh} ({{r}_{{nj}}}x) + Q_{{nj}}^{1}{\text{sh}}({{r}_{{nj}}}(x - D))\} cos({{a}_{n}}y)sin({{c}_{j}}z)$
$\psi _{3}^{1} = \sum\limits_ \{ W_{{nj}}^{1}\operatorname{sh} ({{r}_{{nj}}}x) + Y_{{nj}}^{1}{\text{sh}}({{r}_{{nj}}}(x - D))\} sin({{a}_{n}}y)cos({{c}_{j}}z)$
(2.4)
где

${{q}_{{nj}}} = \sqrt {a_{n}^{2} + c_{j}^{2} - k_{1}^{2}} ,\quad {{r}_{{nj}}} = \sqrt {a_{n}^{2} + c_{j}^{2} - k_{2}^{2}} ,\quad {{a}_{n}} = \pi n{\text{/}}a,\quad {{c}_{j}} = \pi j{\text{/}}c$
Фиг. 1

Большими буквами, кроме $D$, $R$ и $T$, обозначены неизвестные постоянные, ${{k}_{1}} = \omega {\text{/}}{{c}_{p}}$ и ${{k}_{2}} = \omega {\text{/}}{{c}_{s}}$ – продольные и поперечные волновые числа, ${{c}_{p}}$ и ${{c}_{s}}$ $ - $ продольная и поперечная скорости волн в среде $({{c}_{p}} > {{c}_{s}})$, $R$ и $T$ – коэффициенты отражения и прохождения, суммирование ведется по $n + j > 0$.

Следует отметить, что представления (2.2)–(2.4) – точные для произвольных значений волновых чисел ${{k}_{1}}$ и ${{k}_{2}}$, даже в случае, когда квадратные корни ${{q}_{{nj}}}$ и ${{r}_{{nj}}}$ могут принимать комплексные значения. Однако ограничимся рассмотрением случая одной моды: $0 < {{k}_{1}}a < {{k}_{2}}a < \pi $, $0 < {{k}_{1}}c < {{k}_{2}}c < \pi $, тогда ${{q}_{{nj}}} > 0$, ${{r}_{{nj}}} > 0$ для всех $n + j = 1,2,\; \ldots $. При $n = j = 0$ имеем ${{q}_{{00}}} = - i{{k}_{1}}$ и ${{r}_{{00}}} = - i{{k}_{2}}$ в соответствии с условием излучения. Кроме того, принимается, что массивы находятся на достаточно большом расстоянии друг от друга.

Компоненты тензора напряжений и вектора перемещений могут быть выражены через потенциалы Ламе в виде

(2.5)
$\begin{gathered} \frac{{{{\sigma }_{{xx}}}}}{\mu } = (2k_{1}^{2} - k_{2}^{2})\varphi + 2\left( {\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\psi }_{3}}}}{{\partial y\partial x}} - \frac{{{{\partial }^{2}}{{\psi }_{2}}}}{{\partial z\partial x}}} \right) \\ \frac{{{{\sigma }_{{xy}}}}}{\mu } = k_{2}^{2}{{\psi }_{3}} + 2\left( {\frac{{{{\partial }^{2}}\varphi }}{{\partial x\partial y}} + \frac{{{{\partial }^{2}}{{\psi }_{3}}}}{{\partial {{y}^{2}}}} - \frac{{{{\partial }^{2}}{{\psi }_{2}}}}{{\partial z\partial y}}} \right),\quad \frac{{{{\sigma }_{{xz}}}}}{\mu } = - k_{2}^{2}{{\psi }_{2}} + 2\left( {\frac{{{{\partial }^{2}}\varphi }}{{\partial x\partial z}} - \frac{{{{\partial }^{2}}{{\psi }_{2}}}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}{{\psi }_{3}}}}{{\partial z\partial y}}} \right) \\ {{u}_{x}} = \frac{{\partial \varphi }}{{\partial x}} + \frac{{\partial {{\psi }_{3}}}}{{\partial y}} - \frac{{\partial {{\psi }_{2}}}}{{\partial z}}\quad (xyz,\;123) \\ \end{gathered} $

Потенциалы ${{\psi }_{{1,2,3}}}$ следует рассматривать с дополнительным условием

(2.6)
$\frac{{\partial {{\psi }_{1}}}}{{\partial x}} + \frac{{\partial {{\psi }_{2}}}}{{\partial y}} + \frac{{\partial {{\psi }_{3}}}}{{\partial z}} = 0$

Принимая непрерывность поля перемещений ${{u}_{x}}$, ${{u}_{y}}$, ${{u}_{z}}$ вне области трещины, введем неизвестные функции $g_{\chi }^{s}(y,z)$ ($\chi = x,y,z$; $s = 1,2$), такие, что

(2.7)
$x = 0{\text{:}}\;u_{\chi }^{l} - u_{\chi }^{1} = \left\{ {\begin{array}{*{20}{l}} {g_{\chi }^{1}(y,z),\quad (y,z) \in {{S}_{0}}} \\ {0,\quad (y,z) \notin {{S}_{0}}} \end{array}} \right.;\quad x = D{\text{:}}\;u_{\chi }^{1} - u_{\chi }^{r} = \left\{ {\begin{array}{*{20}{l}} {g_{\chi }^{2}(y,z),\quad (y,z) \in {{S}_{0}}} \\ {0,\quad (y,z) \notin {{S}_{0}}} \end{array}} \right.$

Физический смысл этих функций – относительные смещения левого и правого берегов трещины вдоль соответствующих декартовых координат.

Ввиду очевидной симметрии задачи, функция ${{u}_{x}}$ – четная по переменным $y$ и $z$, функция ${{u}_{y}}$ – нечетная по $y$ и четная по $z$, функция ${{u}_{z}}$ – четная по $y$ и нечетная по $z$.

Теперь формулы (2.5) и (2.7) могут быть использованы для представления всех постоянных, входящих в потенциалы (2.2)–(2.4) в терминах функций $g_{\chi }^{s}(y,z)$ $\chi = x,y,z$; $s = 1,2$). По аналогии с плоской задачей [11] можно доказать, что при учете естественной геометрической симметрии в рассматриваемой задаче относительные тангенциальные смещения между берегами трещины всюду равны нулю: $g_{y}^{s} \equiv 0$, $g_{z}^{s} \equiv 0$. Тогда ортогональность тригонометрических функций приводит соотношения (2.7) к следующим равенствам:

$ - i{{k}_{1}}R - H_{0}^{1}{{k}_{1}}sin({{k}_{1}}D) = {{A}^{1}}\quad i{{k}_{1}}{{e}^{{i{{k}_{1}}D}}} - F_{0}^{1}{{k}_{1}}sin({{k}_{1}}D) - i{{k}_{1}}T = {{A}^{2}}$
$({{A}_{{nj}}} + {{H}_{{nj}}}\operatorname{sh} ({{q}_{{nj}}}D)){{q}_{{nj}}} + (B_{{nj}}^{3} + Y_{{nj}}^{1}\operatorname{sh} ({{r}_{{nj}}}D)){{a}_{n}} - (B_{{nj}}^{2} + Q_{{nj}}^{1}\operatorname{sh} ({{r}_{{nj}}}D)){{c}_{j}} = {{e}_{{nj}}}{{B}^{1}}$
(2.8)
$(F_{{nj}}^{1}\operatorname{sh} ({{q}_{{nj}}}D) + {{C}_{{nj}}}){{q}_{{nj}}} + (W_{{nj}}^{1}\operatorname{sh} ({{r}_{{nj}}}D) - D_{{nj}}^{3}){{a}_{n}} - (V_{{nj}}^{1}\operatorname{sh} ({{r}_{{nj}}}D) - D_{{nj}}^{2}){{c}_{j}} = {{e}_{{nj}}}{{B}^{2}}$
${{A}^{s}} = \frac{1}{{4ac}}\iint\limits_{{{S}_{0}}} \,g_{x}^{s}(\eta ,\zeta )d\eta d\zeta ,\quad {{B}^{s}} = \frac{2}{{ac}}\iint\limits_{{{S}_{0}}} \,g_{x}^{s}(\eta ,\zeta )cos({{a}_{n}}\eta )cos({{c}_{j}}\zeta )d\eta d\zeta ;\quad s = 1,2$
${{e}_{{nj}}} = \left\{ \begin{gathered} {\text{1/2}},\quad n,j = 1,2,\; \ldots \hfill \\ {\text{1/4}},\quad n = 0,\quad j = 1,2, \ldots ,\quad j = 0,\quad n = 1,2, \ldots \hfill \\ \end{gathered} \right.$

Запишем граничные условия для поля напряжений и перемещений при $x = 0$, D

$\sigma _{{xx}}^{l} = \sigma _{{xx}}^{1},\quad \sigma _{{xy}}^{l} = \sigma _{{xy}}^{1},\quad \sigma _{{xz}}^{l} = \sigma _{{xz}}^{1},\quad (y,z) \notin {{S}_{0}}\quad (l,1 \leftrightarrow 1,r)$
(2.9)
$\sigma _{{xx}}^{l} = \sigma _{{xx}}^{1} = 0,\quad \sigma _{{xy}}^{l} = \sigma _{{xy}}^{1} = 0,\quad \sigma _{{xz}}^{l} = \sigma _{{xz}}^{1} = 0,\quad (y,z) \in {{S}_{0}}\quad (l,1 \leftrightarrow 1,r)$
$u_{x}^{l} = u_{x}^{1},\quad u_{y}^{l} = u_{y}^{1},\quad u_{z}^{l} = u_{z}^{1},\quad (y,z) \notin {{S}_{0}}\quad (l,1 \leftrightarrow 1,r)$
означающие непрерывность поля напряжений (первая строка формул (2.9)) и поля перемещений (последняя строка) вне трещины.

Подставляя все выражения для постоянных в граничные условия отсутствия напряжений на берегах трещины при $x = 0$ и $x = D$, $(y,z) \in {{S}_{0}}$ и используя основное предположение (1.1), после некоторых рутинных преобразований получаем основную систему интегральных уравнений (ИУ)

(2.10)
$\begin{gathered} \frac{1}{{ac}}\iint\limits_{{{S}_{0}}} \,g_{x}^{s}(\eta ,\zeta )\left\{ {\frac{1}{{{\text{8}}i{{k}_{1}}}} - \frac{{K(y - \eta ,z - \zeta )}}{{k_{2}^{4}}}} \right\}d\eta d\zeta + \frac{{{{e}^{{i{{k}_{1}}D}}}}}{{{\text{8}}aci{{k}_{1}}}}\iint\limits_{{{S}_{0}}} \,g_{x}^{{3 - s}}(\eta ,\zeta )d\eta d\zeta = {{\delta }_{{1s}}} + {{\delta }_{{2s}}}{{e}^{{i{{k}_{1}}D}}} \\ K(y,z) = \sum\limits_{n + j > 0} \,{{e}_{{nj}}}{{L}_{{nj}}}\cos ({{a}_{n}}y)\cos ({{c}_{j}}z),\quad {{L}_{{nj}}} = \frac{{{{R}_{{nj}}}}}{{{{q}_{{nj}}}}}, \\ {{R}_{{nj}}} = {{[2(a_{n}^{2} + c_{j}^{2}) - k_{2}^{2}]}^{2}} - 4{{r}_{{nj}}}{{q}_{{nj}}}(a_{n}^{2} + c_{j}^{2}) \\ \end{gathered} $
$(y,z) \in {{S}_{0}}$, $s = 1,2$, ${{\delta }_{{ij}}}$ – символ Кронекера, ${{R}_{{nj}}}$ – функция Релея.

Рассмотрим вспомогательное ИУ

(2.11)
$\frac{1}{{ack_{2}^{2}}}\iint\limits_{{{S}_{0}}} \,h(\eta ,\zeta )K(y - \eta ,z - \zeta )d\eta d\zeta = 1,\quad (y,z) \in {{S}_{0}}$

Очевидно, что

(2.12)
$g_{x}^{s}(y,z) = \left( {\frac{{{{J}_{s}}}}{{8aci{{k}_{1}}}} + \frac{{{{J}_{{3 - s}}}{{e}^{{i{{k}_{1}}D}}}}}{{8aci{{k}_{1}}}} - {{\delta }_{{1s}}} - {{\delta }_{{2s}}}{{e}^{{i{{k}_{1}}D}}}} \right)k_{2}^{2}h(y,z),\quad s = 1,2,$
где

(2.13)
${{J}_{s}} = \iint\limits_{{{S}_{0}}} \,g_{x}^{s}(\eta ,\zeta )d\eta d\zeta $

Интегрирование соотношений (2.12) по области ${{S}_{0}}$ дает систему линейных алгебраических уравнений относительно неизвестных ${{J}_{s}}$

(2.14)
$\left( {\frac{1}{{k_{2}^{2}}} - \frac{H}{{8aci{{k}_{1}}}}} \right){{J}_{s}} + {{( - 1)}^{s}}\frac{{H{{e}^{{i{{k}_{1}}D}}}}}{{8aci{{k}_{1}}}}{{J}_{{3 - s}}} = - H({{\delta }_{{1s}}} + {{\delta }_{{2s}}}{{e}^{{i{{k}_{1}}D}}}),\quad s = 1,2$
Здесь $H = \iint_{{{S}_{0}}} {h(\eta ,\zeta )d\eta d\zeta }$ – интеграл от решения вспомогательного ИУ (2.11), из которого следует, что функция $h(y,z)$ – вещественнозначная в режиме одной моды, значит, и величина $H$ имеет вещественное значение.

Как только вспомогательное ИУ (2.11) и система (2.14) решены, все необходимые характеристики волнового поля могут быть легко найдены. В частности, коэффициенты отражения и прохождения определяются по формулам

(2.15)
$R = - \frac{{{{J}_{1}} + {{J}_{2}}{{e}^{{i{{k}_{1}}D}}}}}{{8aci{{k}_{1}}}},\quad T = - \frac{{{{J}_{1}}{{e}^{{i{{k}_{1}}D}}} + {{J}_{2}}}}{{8aci{{k}_{1}}}} + {{e}^{{i{{k}_{1}}D}}}$

Можно показать, что для любого вещественного значения $H$ естественное энергетическое условие ${{\left| R \right|}^{2}} + {{\left| T \right|}^{2}} = 1$ удовлетворяется автоматически.

Так как коэффициенты отражения и прохождения данная теория предоставляет в явном виде и единственная численная процедура – построение решения вещественного ИУ (2.11), предлагаемый метод можно назвать полуаналитическим. Эффективный способ преобразования ядра $K(y,z)$ описан в следующем разделе.

3. Эффективное преобразования ядра. Рассматривая ядро $K(y,z)$ в системе ИУ (2.10), прежде всего следует заметить, что

(3.1)
${{L}_{{nj}}} \approx - 2(k_{2}^{2} - k_{1}^{2})(a_{n}^{2} + c_{j}^{2}{{)}^{{1/2}}},\quad (n,j) \to \infty $

Следовательно, сумма, определяющая ядро, может быть представлена в виде

$\begin{gathered} K(y,z) = - 2(k_{2}^{2} - k_{1}^{2})\sum\limits_{n + j > 0} \,{{e}_{{nj}}}{{(a_{n}^{2} + c_{j}^{2})}^{{1/2}}}cos({{a}_{n}}y)cos({{c}_{j}}z) + \\ + \;\sum\limits_{n + j > 0} \,{{e}_{{nj}}}[{{L}_{{nj}}} + 2(k_{2}^{2} - k_{1}^{2})(a_{n}^{2} + c_{j}^{2}{{)}^{{1/2}}}]cos({{a}_{n}}y)cos({{c}_{j}}z) \\ \end{gathered} $
или

(3.2)
$K(y,z) = - 2(k_{2}^{2} - k_{1}^{2})I(y,z) + {{K}_{r}}(y,z),\quad I(y,z) = {{I}_{r}}(y,z) + {{I}_{s}}(y,z)$

Здесь ${{K}_{r}}$ – регулярная функция, функция $I$ – сумма регулярной и нерегулярной функций.

Продемонстрируем математические преобразования для случая $a = c$. Вводя безразмерные переменные $\tilde {y} = y{\text{/}}a$, $\tilde {z} = z{\text{/}}c$ и затем опуская тильды, получаем представление

$\frac{a}{\pi }I(y,z) = \sum\limits_{n + j > 0} \,{{e}_{{nj}}}{{({{n}^{2}} + {{j}^{2}})}^{{1/2}}}cos(\pi ny)cos(\pi jz) = $
$ = \sum\limits_{n = 1}^\infty \,{{e}_{{n0}}}ncos(\pi ny) + \sum\limits_{j = 1}^\infty \,{{e}_{{0j}}}jcos(\pi jz) + \sum\limits_{n = 1}^\infty \sum\limits_{j = 1}^\infty \,{{e}_{{nj}}}{{({{n}^{2}} + {{j}^{2}})}^{{1/2}}}cos(\pi ny)cos(\pi jz) = $
(3.3)
$ = \frac{1}{4}\sum\limits_{n = 1}^\infty \,ncos(\pi ny) - \frac{1}{4}\sum\limits_{j = 1}^\infty \,jcos(\pi jz) + \frac{1}{2}\sum\limits_{n = 0}^\infty \,\sum\limits_{j = 1}^\infty \,{{({{n}^{2}} + {{j}^{2}})}^{{1/2}}}cos(\pi ny)cos(\pi jz)$

Последняя двойная сумма преобразуется так. Для каждого $j \geqslant 1$ сумма по $n$ вычисляется по формуле Пуассона [24]

(3.4)
$\begin{gathered} \sum\limits_{n = 0}^\infty \,p(n) = \frac{{p(0)}}{2} + P(0) + 2\,\sum\limits_{n = 1}^\infty \,P(2\pi n), \\ \begin{array}{*{20}{l}} {p(t) = ({{t}^{2}} + {{j}^{2}}{{)}^{{1/2}}}cos(\pi ty),\quad P(u) = \int\limits_0^\infty \,p(t)cos(ut)dt} \end{array} \\ \end{gathered} $

Беря обобщенное значение расходящегося интеграла $P(u)$, получим

(3.5)
$\begin{array}{*{20}{c}} {P(u) = \mathop {lim}\limits_{\varepsilon \to + 0} \,\int\limits_0^\infty \,{{e}^{{ - \varepsilon t}}}{{{({{t}^{2}} + {{j}^{2}})}}^{{1/2}}}cos(\pi ty)cos(ut)dt = - \frac{j}{2}\left[ {\frac{{{{K}_{1}}(j\left| {\pi y + u} \right|)}}{{\left| {\pi y + u} \right|}} + \frac{{{{K}_{1}}(j\left| {\pi y - u} \right|)}}{{\left| {\pi y - u} \right|}}} \right]} \\ \end{array},$
где применены табличные интегралы и функция Макдональда ${{K}_{1}}(\xi )$ [25, 26].

После преобразований последняя сумма по $n$ в представлении (3.3) принимает вид ($j \geqslant 1$)

$\sum\limits_{n = 0}^\infty \,{{({{n}^{2}} + {{j}^{2}})}^{{1/2}}}cos(\pi ny) = j\left[ {\frac{1}{2} - \frac{{{{K}_{1}}(j\pi \left| y \right|)}}{{\pi \left| y \right|}} - \sum\limits_{n = 1}^\infty \,{{\chi }_{n}}(j,y)} \right],$
${{\chi }_{n}}(j,y) = \frac{{{{K}_{1}}(j\left| {2\pi n + \pi y} \right|)}}{{\left| {2\pi n + \pi y} \right|}} + \frac{{{{K}_{1}}(j\left| {2\pi n - \pi y} \right|)}}{{\left| {2\pi n - \pi y} \right|}}$

Окончательно, функция $I(y,z)$ в равенствах (3.2) представляется в виде

(3.6)
$\begin{gathered} \frac{a}{\pi }I(y,z) = \frac{1}{4}{{\Sigma }_{1}}(y) - \frac{1}{{2\pi \left| y \right|}}{{\Sigma }_{2}}(y,z) - \frac{1}{2}\sum\limits_{n,j = 1}^\infty \,{{\chi }_{n}}(j,y)jcos(\pi jz) \\ {{\Sigma }_{1}}(y) = \sum\limits_{n = 1}^\infty \,ncos(\pi ny),\quad {{\Sigma }_{2}}(y,z) = \sum\limits_{j = 1}^\infty \,j{{K}_{1}}\left( {j\pi \left| y \right|} \right)cos(\pi jz) \\ \end{gathered} $

Функции ${{\Sigma }_{1}}(y)$ и ${{\Sigma }_{2}}(y,z)$ вычисляются явно через сведение к табличным рядам [25]:

${{\Sigma }_{1}}(y) = \mathop {lim}\limits_{\varepsilon \to + 0} \,\sum\limits_{n = 1}^\infty \,{{e}^{{ - \varepsilon n}}}ncos(\pi ny) = - \frac{1}{{4si{{n}^{2}}(\pi y{\text{/}}2)}},$
${{\Sigma }_{2}}(y,z) = - \frac{{{\text{sign}}(y)}}{\pi }\frac{\partial }{{\partial y}}\sum\limits_{j = 1}^\infty \,{{K}_{0}}(j\pi \left| y \right|)cos(\pi jz) = $
(3.7)
$ = - \frac{{{\text{sign}}(y)}}{{2\pi }}\frac{\partial }{{\partial y}}\left\{ {\frac{1}{{{{{({{y}^{2}} + {{z}^{2}})}}^{{1/2}}}}} + {\text{C}} + ln\frac{{\left| y \right|}}{4} + \sum\limits_{j = 1}^\infty \left( {{{\Theta }_{ + }}(j,y,z) + {{\Theta }_{ - }}(j,y,z) - \frac{1}{j}} \right)} \right\} = $
$ = \frac{1}{{2\pi }}\left\{ {\frac{{\left| y \right|}}{{{{{({{y}^{2}} + {{z}^{2}})}}^{{3/2}}}}} - \frac{1}{{\left| y \right|}} + \left. {\sum\limits_{j = 1}^\infty \,{\text{(}}\left| y \right|[\Theta _{ + }^{3}(j,y,z) + \Theta _{ - }^{3}(j,y,z)])} \right\}} \right.,$
${{\Theta }_{ \pm }}(j,y,z) = \frac{1}{{{{{[{{y}^{2}} + {{{(2j \pm z)}}^{2}}]}}^{{1/2}}}}},$
где ${\text{C}} = 0.5772\; \ldots $ – постоянная Эйлера [26].

Таким образом, для ядра (3.2) основного ИУ (2.11) имеем

(3.8)
$K(y,z) = {{K}_{r}}(y,z) - 2(k_{2}^{2} - k_{1}^{2})[{{I}_{r}}(y,z) + {{I}_{s}}(y,z)]$
где

$\frac{a}{\pi }{{I}_{r}} = - \frac{1}{{4{{\pi }^{2}}}}\sum\limits_{j = 1}^\infty (\Theta _{ + }^{3}(j,y,z) + \Theta _{ - }^{3}(j,y,z)) - \;\frac{1}{2}\sum\limits_{n,j = 1}^\infty jcos(\pi jz){{\chi }_{n}}(j,y) + \frac{1}{{4{{\pi }^{2}}{{y}^{2}}}} - \frac{1}{{16si{{n}^{2}}(\pi y{\text{/}}2)}}$
$\frac{a}{\pi }{{I}_{s}} = - \frac{1}{{4{{\pi }^{2}}{{{({{y}^{2}} + {{z}^{2}})}}^{{3/2}}}}}$

Полученное сингулярное представление ядра при малых аргументах содержит двумерный гиперсингулярный член $1{\text{/}}{{({{y}^{2}} + {{z}^{2}})}^{{3/2}}}$, хорошо известный в линейной теории упругости для трещин в неограниченной среде [27].

4. Численное решение вспомогательного уравнения. Основное ИУ (2.11) при использовании нового представления ядра (2.16), (2.17) перепишем в безразмерной форме ($c = a = 1$)

(4.1)
$\begin{gathered} \frac{1}{{k_{2}^{2}}}\iint\limits_{{{S}_{0}}} {h(\eta ,\zeta )}\left\{ {{{\Phi }_{r}}(y - \eta ,z - \zeta ) + \frac{{k_{2}^{2} - k_{1}^{2}}}{{2\pi {{\Delta }^{3}}(\eta ,\zeta ,y,z)}}} \right\}d\eta d\zeta = 1,\quad (y,z) \in {{S}_{0}} \\ {{\Phi }_{r}}(y,z) = - 2(k_{2}^{2} - k_{1}^{2}){{I}_{r}}(y,z) + {{K}_{r}}(y,z),\quad \Delta (\eta ,\zeta ,y,z) = {{[{{(y - \eta )}^{2}} + {{(z - \zeta )}^{2}}]}^{{1/2}}} \\ \end{gathered} $

Для обеспечения устойчивого счета в представленных численных расчетах используются дискретные квадратурные формулы для двумерных гиперсингулярных ядер, основанные на применении “метода дискретных вихрей” [27], согласно которому, при дискретизации уравнения (4.1) устойчивое поведение гиперсингулярных ядер достигается за счет выбора двух различных сеток узлов для “внутренних” $\eta $, $\zeta $ и “внешних” $y$, $z$ переменных. Более точно, если разделить интервал интегрирования $( - b,b)$ на ${{N}_{1}}$ равных малых подинтервалов и интервал $( - d,d)$ на ${{N}_{2}}$ подынтервалов, и, если “внутренние” узлы по каждой из декартовых координат $y$ и $z$ взяты точно в концах соответствующих подинтервалов, тогда “внешние” узлы следует брать каждый раз в середине между двумя соседними “внутренними” узлами:

$\begin{gathered} {{\eta }_{k}} = - b + k{{\varepsilon }_{1}},\quad {{y}_{l}} = - b + (l - {\text{1/2}}){{\varepsilon }_{1}},\quad {{\varepsilon }_{1}} = 2b{\text{/}}{{N}_{1}} \\ {{\zeta }_{m}} = - d + m{{\varepsilon }_{2}},\quad {{z}_{p}} = - d + (p - {\text{1/2}}){{\varepsilon }_{2}},\quad {{\varepsilon }_{2}} = 2d{\text{/}}{{N}_{2}} \\ k = 0, \ldots ,{{N}_{1}},\quad l = 1, \ldots ,{{N}_{1}},\quad m = 0, \ldots ,{{N}_{2}},\quad p = 1, \ldots ,{{N}_{2}} \\ \end{gathered} $

Такая дискретизация в равенстве (4.1) означает

(4.2)
$\frac{1}{{k_{2}^{2}}}\,\sum\limits_{k = 1}^{{{N}_{1}}} \sum\limits_{m = 1}^{{{N}_{2}}} \,h({{\eta }_{k}},{{\zeta }_{m}})\left\{ {{{\varepsilon }_{1}}{{\varepsilon }_{2}}{{\Phi }_{r}}({{y}_{l}} - {{\eta }_{k}},{{z}_{p}} - {{\zeta }_{m}}) + \frac{{k_{2}^{2} - k_{1}^{2}}}{{2\pi }}\int\limits_{{{\eta }_{{k - 1}}}}^{{{\eta }_{k}}} \,\int\limits_{{{\zeta }_{{m - 1}}}}^{{{\zeta }_{m}}} \frac{{d\eta d\zeta }}{{{{\Delta }^{3}}(\eta ,\zeta ,{{y}_{l}},{{z}_{p}})}}} \right\} = 1$

Было показано [24, 28], что здесь интегрирование гиперсингулярных ядер можно провести с использованием стандартных первообразных, так же как и для обычных непрерывных функций. Для двойного интеграла используется табличный интеграл [25]

(4.3)
$\begin{array}{*{20}{l}} {\iint \frac{{d\eta d\zeta }}{{{{\Delta }^{3}}(\eta ,\zeta ,{{y}_{l}},{{z}_{p}})}} = - \frac{{\Delta (\eta ,\zeta ,{{y}_{l}},{{z}_{p}})}}{{({{y}_{l}} - \eta )({{z}_{p}} - \zeta )}}} \end{array}$

В результате уравнение (4.2) сводится в дискретной форме к следующей системе линейных алгебраических уравнений:

(4.4)
$\begin{gathered} \frac{1}{{k_{2}^{2}}}\sum\limits_{k,m = 1}^N \,h({{\eta }_{k}},{{\zeta }_{m}})\left\{ {{{\varepsilon }_{1}}{{\varepsilon }_{2}}{{\Phi }_{r}}({{y}_{l}} - {{\eta }_{k}},{{z}_{p}} - {{\zeta }_{m}}) + \frac{{k_{2}^{2} - k_{1}^{2}}}{{2\pi }}\left[ { - \frac{{\Delta ({{\eta }_{k}},{{\zeta }_{m}},{{y}_{l}},{{z}_{p}})}}{{({{\eta }_{k}} - {{y}_{l}})({{\zeta }_{m}} - {{z}_{p}})}} + } \right.} \right. \\ + \;\frac{{\Delta ({{\eta }_{k}},{{\zeta }_{{m - 1}}},{{y}_{l}},{{z}_{p}})}}{{({{\eta }_{k}} - {{y}_{l}})({{\zeta }_{{m - 1}}} - {{z}_{p}})}} + \frac{{\Delta ({{\eta }_{{k - 1}}},{{\zeta }_{m}},{{y}_{l}},{{z}_{p}})}}{{({{\eta }_{{k - 1}}} - {{y}_{l}})({{\zeta }_{m}} - {{z}_{p}})}} - \left. {\left. {\frac{{\Delta ({{\eta }_{{k - 1}}},{{\zeta }_{{m - 1}}},{{y}_{l}},{{z}_{p}})}}{{({{\eta }_{{k - 1}}} - {{y}_{l}})({{\zeta }_{{m - 1}}} - {{z}_{p}})}}} \right]} \right\} = 1 \\ \end{gathered} $

Было доказано [24], что применяемый метод дискретных вихрей автоматически обеспечивает выполнение требуемого условия: раскрытие трещины должно стремиться к нулю с приближением к внешней границе (периметру области ${{S}_{0}}$). В начальной непрерывной форме (см. уравнения (2.11) и (2.12)) это следует из качественных свойств соответствующих гиперсингулярных уравнений, а в дискретной форме это обеспечивается использованием специфического численного метода [25].

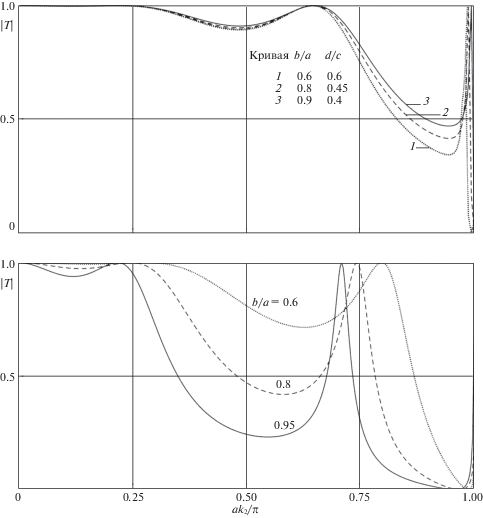
Некоторые примеры расчета представлены на фиг. 2 и фиг. 3 при отношении скоростей в упругом материале ${{c}_{p}}{\text{/}}{{c}_{s}} = 1.870$. Верхняя часть фиг. 2 отражает поведение коэффициента прохождения $\left| T \right|$ как функцию параметра частоты для прямоугольной трещины разной конфигурации при постоянной площади области (прямоугольника со сторонами $2b$, $2d$): $(bd){\text{/}}(ac) = 0.36$ при ${{S}_{0}} = 0.36$, $a = c = 1$, $D{\text{/}}a = 4$. В нижней части показано поведение коэффициента прохождения в зависимости от параметра частоты для квадратных трещин при $b = d$, $a = c$, $D{\text{/}}a = 3$ и разных относительных размерах трещины.

Фиг. 2
Фиг. 3

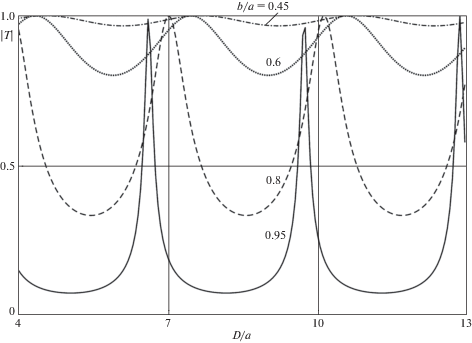
Коэффициент прохождения как функция расстояния между массивами для фиксированных значений относительного размера квадратной трещины $b{\text{/}}a$ изображен на фиг. 3 при $b = d$, $a = c$, $a{{k}_{2}}{\text{/}}\pi = 0.6$.

Здесь не демонстрируются графики для коэффициента отражения $\left| R \right|$, так как он связан с коэффициентом прохождения $\left| T \right|$ простым соотношением: $\left| T \right|$ = ${{(1 - {{\left| R \right|}^{2}})}^{{1/2}}}$.

5. Заключение. Необходимо оценить, в каком физическом режиме материал с рассмотренной внутренней структурой может иметь свойства акустического фильтра. Физически, метаматериалы, работающие как акустический фильтр, значительно подавляют проникающую волну (низкое значение $\left| T \right|$), т.е. имеет место так называемое запирание в определенных диапазонах частот. Если зафиксировать область трещины ${{S}_{0}} = bd$ и расстояние $D$ ($D{\text{/}}a = 4$), то поведение функции $\left| {T(a{{k}_{2}}{\text{/}}\pi )} \right|$ демонстрирует свойство акустического фильтра для разных соотношений между сторонами прямоугольной области ${{S}_{0}}$ (верхняя часть фиг. 2). Нетрудно оценить, что расхождение значений коэффициента $\left| T \right|$ для прямоугольных трещин одинаковой площади, но разной конфигурации, может достигать 30%.

Если задать величины $b{\text{/}}a$ и $a{{k}_{2}}$, то поведение коэффициента $\left| T \right|$ в зависимости от расстояния между параллельными массивами $D{\text{/}}a$ показывает (фиг. 3), что для длинных трещин имеет место почти полное запирание на большей части интервала изменения параметра $D{\text{/}}a$, кроме некоторых узких участков, где $\left| T \right|$ приближается к единичному значению.

Из графиков нижней части фиг. 2 следует, что подавляемый коэффициент прохождения $\left| {T(a{{k}_{2}}{\text{/}}\pi )} \right|$ на трех частотных диапазонах одномодового интервала спадает больше с увеличением относительного размера трещины. В случае $D{\text{/}}a = 3$ для квадратных трещин разных размеров диапазон частот наиболее сильного запирания расположен в верхней части одномодового интервала (0.85 < $a{{k}_{2}}{\text{/}}\pi $ < 0.99). Это происходит в случае трещин среднего ($b{\text{/}}a = 0.8$ при ${{S}_{0}}{\text{/}}S = (bd){\text{/}}(ac)$ = 0.64) и большого ($b{\text{/}}a$ = 0.9 при ${{S}_{0}}{\text{/}}S = (bd){\text{/}}(ac)$ = 0.81) размера. Можно заметить, что для более крупных трещин этот интервал длиннее.

Из проведенного анализа следует, что требуемое управление свойствами акустического фильтра в рассматриваемой системе достигается выбором как длины трещины, так и расстояния между двумя соседними вертикальными массивами, содержащими периодические системы трещин. Предлагаемый метод может применяться и для более сложных волновых задач с большим числом параллельных вертикальных массивов, содержащих двоякопериодические системы трещин.

В принятой здесь постановке автором совместно с М.А. Сумбатяном была рассмотрена двумерная задача для двух параллельных массивов трещин [29] и задача о распространении волн через двоякопериодический и троякопериодический массивы трещин в трехмерной постановке [30, 31], а также представлено развитие полуаналитического метода решения задач высокочастотной дифракции упругих волн на трещине [32].

Автор благодарит М.А. Сумбатяна за замечания.

Работа выполнена при поддержке Министерства образования и науки РФ (9.5794.2017/8.9).

Список литературы

  1. Шендеров Е.Л. Прохождения звука через жесткий экран конечной толщины с отверстиями // Акуст. ж. 1970. Т. 16. № 2. С. 295–304.

  2. Miles J.W. On Rayleigh scattering by a grating // Wave Motion. 1982. № 4. P. 285–292.

  3. Achenbach J.D., Li Z.L. Reflection and transmission of scalar waves by a periodic array of screens // Wave Motion. 1986. № 8. P. 225–234.

  4. Kok Y.-L., Gallagher N.C., Jr., Ziolkowski R.V. Dual series solution to the scattering of plane wave from a binary conducting grating // IEEE Trans. Anten. Prop. 1989. AP-37. P. 901–917.

  5. Zarrillo G., Aguiar K. Closed-form low frequency solutions for electromagnetic waves through a frequency selective surface // IEEE Trans. Anten. Prop. 1988. AP. 35. P. 1406–1417.

  6. Scarpetta E., Sumbatyan M.A. Explicit analytical results for one-mode normal reflection and transmission by a periodic array of screens // J. Math. Anal. Appl. 1995. № 195. P. 736–749.

  7. Scarpetta E., Sumbatyan M.A. On wave propagation in elastic solids with a doubly periodic array of cracks // Wave Motion. 1997. № 25. P. 61–72.

  8. Scarpetta E., Tibullo V. Explicit results for scattering parameters in three-dimensional wave propagation through a doubly periodic system of arbitrary openings // Acta Mechanica. 2006. № 185. P. 1–9.

  9. Scarpetta E., Tibullo V. On the three-dimensionl wave propagation through cascading screens having a periodic system of arbitrary openings // Int. J. Eng. Sci. 2008. № 46. P. 105–111.

  10. Angel Y.C., Bolshakov A. In-plane waves in an elastic solid containing a cracked slab region // Wave Motion. 2000. № 31. P. 297–315.

  11. Scarpetta E. In-plane problem for wave propagation through elastic solids with a periodic array of cracks // Acta Mech. 2002. № 154. P. 179–187.

  12. Angel Y.C., Achenbach J.D. Harmonic waves in an elastic solid containing a doubly periodic array of cracks // Wave Motion. 1987. № 9. P. 377–385.

  13. Homentcovschi D., Miles R.N. Influence of viscosity on the diffraction of sound by a periodic array of screens. The general 3-D problem // J. Acoust. Soc. Am. 2005. V 117. № 5. P. 2761–2771.

  14. Sotiropoulos D.A., Achenbach J.D. Ultrasonic reflection by a planar distribution of cracks // J. NDE. 1988. № 7. P. 123–129.

  15. Mykhas’kiv V.V., Zhbadynskyi I.Ya., Zhang Ch. Dynamic stresses due to time-harmonic elastic wave incidence on doubly periodic array of penny-shaped cracks // J. Math. Sci. 2014. № 203. P. 114–122.

  16. Liu Z., Zhang X., Mao Y., Zhu Y.Y., Yang Z., Chan C.T., Sheng P. Locally resonant sonic materials // Science. 2000. V. 289. № 5485. P. 1734–1736.

  17. McPhedran R.C., Movchan A.B., Movchan N.V. Platonic crystals: Bloch bands, neutrality and defects // Mech. Mater. 2009. № 41. P. 356–363.

  18. McPhedran R.C., Movchan A.B., Movchan N.V. Wave scattering by platonic grating stacks // Proc. Roy. Soc. 2009. № 465. P. 3383–3400.

  19. Craster R.V., Guenneau S. Acoustic Metamaterials. Springer Series in Materials Science 166. Dordrecht: Springer, 2013.

  20. Piau M. Attenuation of a plane compressional wave by a random distribution in thin circular cracks // Int. J. Eng. Sci. 1979. № 17. P. 151–167.

  21. Gubernatis J.E. Long-wave approximations for the scattering of elastic waves from flaws with applications to ellipsoidal voids and inclusions // J. Appl. Phys. 1979. № 50. P. 4046–4058.

  22. Willis J.R. A polarization approach to the scattering of elastic waves – II. Multiple scattering from inclusions // J. Mech. Phys. Solids.1980. № 28. P. 307–327.

  23. Кузнецов С.В. Рассеивание волн в пористых средах // Изв. РАН. МТТ. 1995. № 3. P. 81–86.

  24. Сумбатян М.А., Скалия А. Основы теории дифракции с приложениями в механике и акустике. М.: Физматлит, 2013. 328 с.

  25. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Т. 1, 2. М.: Наука, 1980.

  26. Abramowitz M., Stegun I.A. Handbook of Mathematical Functions. Washington, D.C.: National Bureau of Standards, 1979.

  27. Sneddon I.N., Lowengrub M. Crack problems in the classical theory of elasticity. L.: Wiley, 1969.

  28. Белоцерковский С.М., Лифанов И.К. Численные методы в сингулярных интегральных уравнениях и их применение в аэродинамике, теории упругости, электродинамике. М.: Наука, 1985.

  29. Sumbatyan M.A., Remizov M.Yu. On the theory of acoustic metamaterials with a triple-periodic system of interior obstacles // Advan. Struct. Mater. 2017. № 41. P. 19–33.

  30. Remizov M.Yu., Sumbatyan M.A. 3-D one-mode penetration of elastic waves through a doubly periodic array of cracks // Math. Mech. Solids. 2018. № 23(4). P. 636–650.

  31. Remizov M.Yu., Sumbatyan M.A. On 3d Theory of Acoustic Meta-materials with a Triple-Periodic System of Interior Obstacles // Proc. National Acad. Sci. Armenia. Mech. 2017. № 70(4). P. 35–49.

  32. Ремизов М.Ю., Сумбатян М.А. Полуаналитический метод решения задач высокочастотной дифракции упругих волн на трещине // ПММ. 2013. Т. 77. № 4. С. 629–635.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал