1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 1, 2019

Прикладная математика и механика, 2019, T. 83, № 1, стр. 63-71

КРАЕВЫЕ ЗАДАЧИ ДИНАМИЧЕСКОГО ПОВЕДЕНИЯ ДВУМЕРНЫХ УПРУГИХ СИСТЕМ С ДВИЖУЩИМИСЯ ОБЪЕКТАМИ

Е. Е. Лисенкова 1, 2, *

1 Институт проблем машиностроения РАН
Н. Новгород, Россия

2 Нижегородский институт управления – филиал РАНХиГС
Н. Новгород, Россия

* E-mail: EELissen@yandex.ru

Поступила в редакцию 11.11.2017

Полный текст (PDF)

Аннотация

Рассматривается взаимообусловленное динамическое поведение двумерной упругой системы в форме полосы и движущегося по ней одномерного механического объекта. Плотность функции Лагранжа двумерной системы зависит от обобщенных координат и их производных до второго порядка включительно, а лагранжиан движущегося объекта в качестве одной из обобщенных координат содержит закон движения, являющийся неизвестной функцией задачи. Получены физически и математически корректные условия на движущейся границе как результат постановки самосогласованной краевой задачи, основанной на вариационном принципа Гамильтона. В качестве примера приводится постановка задачи о безотрывном движении стержня, совершающего изгибные и крутильные колебания, вдоль пластины, при учете инерции вращения ее элементов. Выведены дифференциальные и интегральные законы изменения энергии и волнового импульса как для всей сложной системы в целом, так и для отдельных ее частей. Найдены соотношения между компонентами вектора плотности потока энергии и тензора плотности потока волнового импульса, справедливые на движущейся границе.

Ключевые слова: краевая задача, двумерная упругая система, движущийся объект, пластина, энергия, волновой импульс

Развитый ранее подход к постановкам краевых задач динамики двумерных систем с движущимися нагрузками и закреплениями, основанным на вариационном принципе Гамильтона–Остроградского [1, 2], обобщается ниже на случай, когда лагранжианы двумерной и одномерной систем зависят от обобщенных координат и их производных до второго порядка, включая и смешанные производные по пространственной и временной переменным. Обсуждаются эффекты, связанные с учетом этих дополнительных производных.

1. Постановка задачи. Краевые условия на движущихся границах. Рассмотрим двумерную систему, состоящую из полосы шириной $0 \leqslant y \leqslant {{b}_{0}}$ и длиной ${{x}_{1}} \leqslant x \leqslant {{x}_{2}}$, вдоль которой безотрывно движется по неизвестному закону $x = \ell (y,t)$ одномерный механический объект, например, струна, балка и т.п.

В пространстве xyt, где x, y – пространственные переменные, t – время, рассмотрим область

$D = \{ {\text{(}}x,y,t{\text{):}}\;{{x}_{1}} \leqslant x \leqslant {{x}_{2}},\;0 \leqslant y \leqslant {{b}_{0}},\;{{t}_{1}} \leqslant t \leqslant {{t}_{2}}\} $
и ее проекцию на плоскость yt

${{D}_{0}} = \{ {\text{(}}y,t{\text{):}}\;0 \leqslant y \leqslant {{b}_{0}},\;{{t}_{1}} \leqslant t \leqslant {{t}_{2}}\} $

Поверхность $x = \ell (y,t)$, $(y,t) \in {{D}_{0}}$ делит область D на части ${{D}_{1}}$ и ${{D}_{2}}$ [2]. Колебания двумерной системы описываются некоторой непрерывной в D вектор-функцией

$\begin{gathered} {\mathbf{u}}(x,y,t) = {{{\mathbf{u}}}^{j}}(x,y,t) = \{ u_{1}^{j}(x,y,t),\; \ldots ,\;u_{n}^{j}(x,y,t)\} , \\ (x,y,t) \in {{D}_{j}},\quad j = \left\{ {\begin{array}{*{20}{c}} {1\quad {\text{п р и }}\quad x < \ell (y,t)} \\ {2\quad {\text{п р и }}\quad x > \ell (y,t)} \end{array}} \right. \\ \end{gathered} $
причем вектор-функции ${{{\mathbf{u}}}^{j}}(x,y,t)$ дважды непрерывно дифференцируемы в областях ${{D}_{j}}$ ($j = 1,2$) соответственно. Будем полагать, что плотность функции Лагранжа
$\lambda (x,y,t,{\mathbf{u}},{{{\mathbf{u}}}_{x}},{{{\mathbf{u}}}_{y}},{{{\mathbf{u}}}_{t}},{{{\mathbf{u}}}_{{xx}}},{{{\mathbf{u}}}_{{xt}}},{{{\mathbf{u}}}_{{xy}}},{{{\mathbf{u}}}_{{yt}}},{{{\mathbf{u}}}_{{yy}}}),\quad \lambda = \left\{ {\begin{array}{*{20}{c}} {{{\lambda }^{1}}\quad {\text{п р и }}\quad x < \ell (y,t)} \\ {{{\lambda }^{2}}\quad {\text{п р и }}\quad x > \ell (y,t)} \end{array}} \right.$
двумерной системы зависит от вектор-функции обобщенных координат и ее производных до второго порядка включительно. В отличие от предыдущего подхода [1, 2] здесь учитываются смешанные производные обобщенных координат по пространственной и временной переменным. Одномерный объект характеризуется плотностью функции Лагранжа
$L = L(y,t,\ell ,{{\ell }_{t}},{{\ell }_{y}},{{\ell }_{{yy}}},{{\ell }_{{yt}}},{\mathbf{u}}{}^{0},{\mathbf{u}}_{t}^{0},{\mathbf{u}}_{y}^{0},{\mathbf{u}}_{{yy}}^{0},{\mathbf{u}}_{{yt}}^{0},{{{\mathbf{w}}}^{0}},{\mathbf{w}}_{t}^{0},{\mathbf{w}}_{y}^{0},{\mathbf{w}}_{{yy}}^{0},{\mathbf{w}}_{{yt}}^{0})$
одна из обобщенных координат которой – закон движения $\ell (y,t)$, являющийся неизвестной функцией задачи. Здесь
${{{\mathbf{u}}}^{0}}(y,t) = {\mathbf{u}}(\ell (y,t),y,t) = {{{\mathbf{u}}}^{j}}(\ell (y,t),y,t)$
${{{\mathbf{w}}}^{0}}(y,t) = {{{\mathbf{u}}}_{x}}(\ell (y,t),y,t) = {\mathbf{u}}_{x}^{j}(\ell (y,t),y,t);\quad j = 1,2$
L и ${{\lambda }^{j}}$ – дважды непрерывно дифференцируемые функции по совокупности своих аргументов.

Динамическое поведение направляющей и движущегося по ней объекта взаимообусловлено [1, 2], а именно: характер колебаний двумерной системы зависит от закона движения объекта, а движение последнего происходит под действием как внешних сил, так и сил реакции со стороны направляющей.

Введем обозначения дифференциальных операторов

$\begin{gathered} {{\partial }_{x}} = \frac{\partial }{{\partial x}},\quad {{\partial }_{y}} = \frac{\partial }{{\partial y}},\quad {{\partial }_{t}} = \frac{\partial }{{\partial t}},\quad {{\partial }_{{xx}}} = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}},\quad {{\partial }_{{xy}}} = \frac{{{{\partial }^{2}}}}{{\partial x\partial y}}, \\ {{\partial }_{{yy}}} = \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}},\quad {{\partial }_{{xt}}} = \frac{{{{\partial }^{2}}}}{{\partial x\partial t}},\quad {{\partial }_{{yt}}} = \frac{{{{\partial }^{2}}}}{{\partial y\partial t}} \\ \end{gathered} $

Записывая вариационный принцип Гамильтона для всей системы и решая соответствующую вариационную задачу [2–5] в предположении, что обобщенные координаты заданы в начальный ($t = {{t}_{1}}$) и конечный ($t = {{t}_{2}}$) моменты времени и на границах полосы (${{x}_{1}} \leqslant x \leqslant {{x}_{2}}$, $0 \leqslant y \leqslant {{b}_{0}}$), находим, что вектор-функция обобщенных координат удовлетворяет уравнению

(1.1)
$\begin{gathered} {{\lambda }_{{\mathbf{u}}}} - {{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{x}}}}} - {{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{y}}}}} - {{\partial }_{t}}{{\lambda }_{{{{{\mathbf{u}}}_{t}}}}} + {{\partial }_{{xx}}}{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}} + {{\partial }_{{xy}}}{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}} + {{\partial }_{{yy}}}{{\lambda }_{{{{{\mathbf{u}}}_{{yy}}}}}} + {{\partial }_{{xt}}}{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}} + {{\partial }_{{yt}}}{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}} = - {\mathbf{q}} \\ (x,y,t) \in \operatorname{Int} {{D}_{j}},\quad j = 1,2 \\ \end{gathered} $
и условиям на движущейся границе $x = \ell (t,y)$, $(y,t) \in {{D}_{0}}$
(1.2)
${{L}_{{{{{\mathbf{u}}}^{0}}}}} - {{\partial }_{t}}{{L}_{{{\mathbf{u}}_{t}^{0}}}} - {{\partial }_{y}}{{L}_{{{\mathbf{u}}_{y}^{0}}}} + {{\partial }_{{yy}}}{{L}_{{{\mathbf{u}}_{{yy}}^{0}}}} + {{\partial }_{{yt}}}{{L}_{{{\mathbf{u}}_{{yt}}^{0}}}} = [{\mathbf{N}}] - {{{\mathbf{q}}}_{{\mathbf{1}}}}\quad ({\mathbf{u}},{\mathbf{N}},{{{\mathbf{q}}}_{{\mathbf{1}}}} \leftrightarrow {\mathbf{w}},{\mathbf{M}},{{{\mathbf{q}}}_{{\mathbf{2}}}})$
(1.3)
${{L}_{\ell }} - {{\partial }_{t}}{{L}_{{{{\ell }_{t}}}}} - {{\partial }_{y}}{{L}_{{{{\ell }_{y}}}}} + {{\partial }_{{yy}}}{{L}_{{{{\ell }_{{yy}}}}}} + {{\partial }_{{yt}}}{{L}_{{{{\ell }_{{yt}}}}}} = [F] - {{q}_{3}}$
(1.4)
${\mathbf{u}}(\ell - 0,y,t) = {\mathbf{u}}(\ell + 0,y,t) = {{{\mathbf{u}}}^{0}}(y,t),\quad {{{\mathbf{u}}}_{x}}(\ell - 0,y,t) = {{{\mathbf{u}}}_{x}}(\ell + 0,y,t) = {{{\mathbf{w}}}^{0}}(y,t)$
где

$F = \lambda - ({{{\mathbf{u}}}_{x}},{\mathbf{N}}) - ({{{\mathbf{u}}}_{{xx}}},{\mathbf{M}})$
${\mathbf{N}} = {{\lambda }_{{{{{\mathbf{u}}}_{x}}}}} - {{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}} - {{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}} - {{\partial }_{t}}{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}} - {{\ell }_{y}}({{\lambda }_{{{{{\mathbf{u}}}_{y}}}}} - 2{{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{yy}}}}}} - {{\partial }_{t}}{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}}) + $
$ + \;{{\ell }_{{yy}}}{{\lambda }_{{{{{\mathbf{u}}}_{{yy}}}}}} + \ell _{y}^{2}{{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{{yy}}}}}} - {{\ell }_{t}}({{\lambda }_{{{{{\mathbf{u}}}_{t}}}}} - {{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}} - {{\ell }_{y}}{{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}}) + {{\ell }_{{yt}}}{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}}$
${\mathbf{M}} = {{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}} - {{\ell }_{y}}({{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}} - {{\ell }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{yy}}}}}}) - {{\ell }_{t}}({{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}} - {{\ell }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}})$
$[A(x,y,t)] = A(\ell (y,t) + 0,y,t) - A(\ell (y,t) - 0,y,t)$
${{\lambda }_{{\mathbf{a}}}} = \left( {\frac{{\partial \lambda }}{{\partial {{a}_{1}}}}, \ldots ,\frac{{\partial \lambda }}{{\partial {{a}_{n}}}}} \right),\quad {{L}_{{\mathbf{a}}}} = \left( {\frac{{\partial L}}{{\partial {{a}_{1}}}}, \ldots ,\frac{{\partial L}}{{\partial {{a}_{n}}}}} \right);\quad {\mathbf{a}} = ({{a}_{1}}, \ldots ,{{a}_{n}})$

Здесь и далее верхний индекс j = 1, 2 для краткости опущен, (·, ·) – скалярное произведение векторов.

В правые части соотношений (1.1)–(1.3), как это обычно делается, введены добавки q, q1 q2, q3, учитывающие действия сторонних и диссипативных сил, учет которых при постановке вариационных задач сопряжен с некоторыми трудностями. N и M – плотности обобщенных сил, действующих со стороны двумерной системы, F – линейная плотность сил давления волн со стороны двумерной направляющей. Уравнение (1.1) описывает динамику двумерной системы, (1.2) и (1.3) – баланса обобщенных сил на движущейся границе, причем (1.3) – закон движения объекта относительно упругой полосы, соотношения (1.4) – условия непрерывности двумерной системы и безотрывного движения вдоль нее объекта. В случае заданного закона движения, уравнение (1.3) определяет силу, необходимую для поддержания такого движения.

Для полной постановки задачи (1.1)–(1.4) следует добавить условия на краях полосы и начальные условия, удовлетворяющие условиям согласования с граничными.

Зависимость функций $\lambda $ и $L$ от дополнительных переменных, которые ранее не учитывались [1, 2], привела к наличию слагаемых, связанных с этими переменными в уравнениях динамики и баланса обобщенных сил. Такое представление позволяет описывать многие линейные и нелинейные модели упругих систем, в том числе с учетом влияния инерции вращения элемента тела [4–13].

В качестве примера рассмотрим движение одномерной нагрузки, представляющей собой механический объект в виде упругого стержня, вдоль однородной пластины толщиной ${{h}_{{\text{*}}}}$, лежащей на винклеровском основании и имеющей форму полосы. Для плотности функции Лагранжа пластины с учетом инерции вращения ее элементов при изгибе имеем выражение [5, 13]

$\lambda = \frac{1}{2}\left\{ {\rho {{h}_{*}}u_{t}^{2} + \frac{{\rho h_{*}^{3}}}{{12}}(u_{{xt}}^{2} + u_{{yt}}^{2}) - \frac{{h_{*}^{3}}}{6}\left( {\frac{{\Lambda + 2\mu }}{2}{{{({{u}_{{xx}}} + {{u}_{{yy}}})}}^{2}} + 2\mu (u_{{xy}}^{2} - {{u}_{{xx}}}{{u}_{{yy}}})} \right) - k{{u}^{2}}} \right\}$

Здесь $\rho {{h}_{*}}$ – поверхностная плотность пластины, $\Lambda $ и $\mu $ – постоянные Ламе, k – коэффициент жесткости (коэффициент “постели”) упругого основания, $u(x,y,t)$ – поперечное смещение пластины. Стержень совершает изгибные и крутильные колебания, плотность его функции Лагранжа имеет вид

$\begin{gathered} L = \frac{1}{2}\{ {{\rho }_{0}}{{F}_{0}}({{({{\partial }_{t}}{{u}^{0}})}^{2}} + \ell _{t}^{2}) + {{\rho }_{0}}{{I}_{x}}{{({{\partial }_{{yt}}}{{u}^{0}})}^{2}} + {{\rho }_{0}}{{I}_{0}}\varphi _{t}^{2} - \\ - \;{{E}_{0}}({{I}_{x}}{{({{\partial }_{{yy}}}{{u}^{0}})}^{2}} + {{I}_{z}}\ell _{{yy}}^{2}) - {{G}_{0}}{{I}_{0}}\varphi _{y}^{2} - {{k}_{0}}{{({{u}^{0}})}^{2}}\} , \\ \end{gathered} $
где ${{\rho }_{0}}{{F}_{0}}$ – погонная плотность стержня, ${{I}_{0}}$ и ${{I}_{x}}$, ${{I}_{z}}$ – полярный момент инерции и моменты инерции поперечного сечения стержня относительно осей х и z, соответственно, ${{E}_{0}}$ – модуль Юнга, ${{G}_{0}}$ и ${{k}_{0}}$ – модуль сдвига и коэффициент, характеризующий жесткость “постели” [6], ${{u}^{0}}(y,t)$ и $\varphi (y,t)$ – поперечное смещение и угол поворота сечения стержня.

Заметим, что при таких допущениях, а именно, использование аналогичных функций Лагранжа (при учете поправки Релея [5, 6]), постановка краевой задачи не может быть получена на основе уравнений, приведенных ранее [1, 2].

Подставляя лагранжианы $\lambda $ и $L$ в соотношения (1.1)–(1.3), получим, что изгибные колебания пластины описываются решением уравнения

(1.5)
$\rho {{h}_{{\text{*}}}}{{u}_{{tt}}} - \frac{{\rho h_{*}^{3}}}{{12}}{{\partial }_{{tt}}}\Delta u + \frac{{(\Lambda + 2\mu )h_{*}^{3}}}{{12}}\Delta \Delta u + ku = 0;\quad {{\partial }_{{tt}}} = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}},\quad \Delta = {{\partial }_{{xx}}} + {{\partial }_{{yy}}}$
удовлетворяющим на движущейся границе $x = \ell (y,t)$ условиям неразрывности пластины и отсутствия у нее изломов
${{u}^{0}}(y,t) = u(\ell - 0,y,t) = u(\ell + 0,y,t),\quad \varphi (y,t) = {{u}_{x}}(\ell - 0,y,t) = {{u}_{x}}(\ell + 0,y,t)$,
а также уравнениям баланса изгибающих моментов и поперечных сил

${{\rho }_{0}}{{I}_{0}}{{\varphi }_{{tt}}} - {{G}_{0}}{{I}_{0}}{{\varphi }_{{yy}}} = - [M] + {{q}_{2}},\quad {{\rho }_{0}}{{F}_{0}}u_{{tt}}^{0} - {{\rho }_{0}}{{I}_{x}}u_{{yytt}}^{0} + {{E}_{0}}{{I}_{x}}u_{{yyyy}}^{0} + {{k}_{0}}{{u}^{0}} = - [N] + {{q}_{1}}$

Уравнение

${{\rho }_{0}}{{F}_{0}}{{\ell }_{{tt}}} + {{\rho }_{0}}{{I}_{z}}{{\ell }_{{yyyy}}} = - [F] + {{q}_{3}}$
определяет закон движения стержня по пластине под действием внешних сил и сил давления изгибных волн пластины. Здесь
$M = - \frac{{h_{*}^{3}}}{{12}}\{ \left( {\Lambda + 2\mu } \right)({{u}_{{xx}}} + \ell _{y}^{2}{{u}_{{yy}}}) - 4\mu {{\ell }_{y}}{{u}_{{xy}}} + \Lambda ({{u}_{{yy}}} + \ell _{y}^{2}{{u}_{{xx}}}) + \rho {{\ell }_{t}}({{u}_{{xt}}} - {{\ell }_{y}}{{u}_{{yt}}})\} $
$N = \frac{{h_{*}^{3}}}{{12}}\{ (\Lambda + 2\mu )({{u}_{{xxx}}} + (1 - \ell _{y}^{2}){{u}_{{xyy}}} - 2{{\ell }_{y}}{{u}_{{yyy}}} - {{\ell }_{{yy}}}{{u}_{{yy}}}) + 2\mu {{u}_{{xyy}}} - $
$ - \;\Lambda (2{{\ell }_{y}}{{u}_{{xxy}}} + {{\ell }_{{yy}}}{{u}_{{xx}}} + \ell _{y}^{2}{{u}_{{xxx}}}) - \rho ({{u}_{{xtt}}} - {{\ell }_{y}}{{u}_{{ytt}}} - {{\ell }_{{yt}}}{{u}_{{yt}}}) - \rho {{\ell }_{t}}(12{{u}_{t}}{\text{/}}h_{*}^{2} - {{u}_{{yyt}}} - {{\ell }_{y}}{{u}_{{xyt}}})\} $
$F = \lambda - ({{u}_{x}}N + {{u}_{{xx}}}M)$
($M$, $N$ и $F$ – соответственно изгибающие моменты, поперечные силы и силы давления волн, действующие на стержень со стороны пластины).

Добавив краевые условия на границах $0 \leqslant y \leqslant {{b}_{0}}$, ${{x}_{1}} \leqslant x \leqslant {{x}_{2}}$ пластины и начальные условия, которые удовлетворяют условиям согласования с граничными, будем иметь полную постановку начально-краевой задачи.

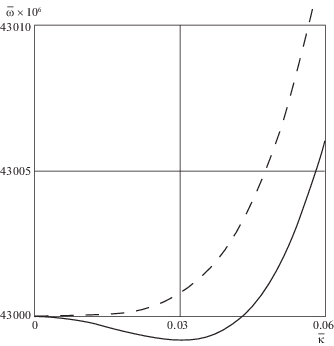
Вопрос о динамическом поведении распределенных упругих систем под действием движущихся объектов тесно связан с изучением в этих системах волновых процессов. Традиционный подход к исследованию последних состоит в получении дисперсионного уравнения, построения дисперсионных кривых и определения критических частот (частот отсечки), при превышении которых возникают бегущие волны. На фигуре 1 для сравнения представлены дисперсионные кривые (зависимость частоты $\omega $ от волнового числа $\kappa $), соответствующие двум моделям пластин (Кирхгофа [2, 4] и модели (1.5)), лежащих на винклеровском основании. Данные кривые построены с использованием безразмерных переменных

$\bar {\omega } = \omega {{h}_{*}}\sqrt {\rho {\text{/(}}\Lambda + 2\mu {\text{)}}} ,\quad \bar {\kappa } = \kappa {{h}_{*}},\quad {{\bar {\omega }}_{*}} = \sqrt {k{{h}_{*}}{\text{/(}}\Lambda + 2\mu {\text{)}}} \quad {\text{п р и }}\quad {{\bar {\omega }}_{*}} = 0.043$
Фиг. 1

Область, в которой низкочастотное поле с частотой

$\omega < {{\omega }_{*}} = \sqrt {k{\text{/(}}\rho {{h}_{*}}{\text{)}}} $
не распространяется, а экспоненциально спадает по мере проникновения в систему, для модели Кирхгофа (штриховая кривая) шире, чем для рассматриваемой модели пластины (1.5) (сплошная кривая). Это связано с тем, что учет инерции вращения (как показали исследования) приводит к меньшей, чем ${{\omega }_{*}}$, частоте
${{\omega }_{{{\text{**}}}}} = \frac{2}{{\sqrt \rho {{h}_{*}}}}{{\left( {6(\Lambda + 2\mu )\left( {\sqrt {1 + \frac{{k{{h}_{*}}}}{{12(\Lambda + 2\mu )}}} - 1} \right)} \right)}^{{1/2}}}$
при переходе через которую возбуждаются бегущие волны. Кроме того, для рассматриваемой модели существует диапазон частот $({{\omega }_{{{\text{**}}}}},{{\omega }_{*}})$, в котором имеет место “эффект обратной волны” [14–16], впервые указанный Лэмбом [17].

2. Законы изменения энергии и волнового импульса. Выявить причины появления динамических эффектов, связанных с взаимодействием волн с движущимися объектами, а также определить интегралы движения, представляющие традиционный интерес при изучении динамического поведения механических систем, помогают законы изменения энергии и импульса. Из уравнений (1.1)–(1.4) можно получить законы изменения энергии и импульса как для всей системы в целом, так и для отдельных ее частей в каждой из областей $\operatorname{Int} {{D}_{j}}$ ($j = 1,2$). Воспользуемся распространенным способом. Умножим скалярно обе части равенства (1.1) на частные производные по t, x и y вектора обобщенных координат ${\mathbf{u}}(x,y,t)$ и после преобразований получим

(2.1)
${{\partial }_{t}}h + div{\mathbf{S}} = - {{\lambda }_{t}} + ({\mathbf{q}},{{{\mathbf{u}}}_{t}}),\quad {{\partial }_{t}}{\mathbf{p}} + div{\mathbf{T}} = {{{\mathbf{F}}}_{{\text{0}}}} - ({\mathbf{q}},grad{\mathbf{u}})$
где

(2.2)
$\begin{gathered} h = ({{{\mathbf{u}}}_{t}},{{\lambda }_{{{{{\mathbf{u}}}_{t}}}}}) + ({{{\mathbf{u}}}_{{xt}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}}) + ({{{\mathbf{u}}}_{{yt}}},{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}}) - \lambda \\ {\mathbf{S}} = \{ {{S}_{x}},{{S}_{y}}\} \\ {{S}_{x}} = \left( {{{{\mathbf{u}}}_{t}},{{\lambda }_{{{{{\mathbf{u}}}_{x}}}}} - {{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}} - \frac{1}{2}{{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}} - {{\partial }_{t}}{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}}} \right) + ({{{\mathbf{u}}}_{{xt}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}}) + \frac{1}{2}({{{\mathbf{u}}}_{{yt}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}})\quad (x \leftrightarrow y) \\ \end{gathered} $
(2.3)
${\mathbf{p}} = \{ {{p}_{x}},{{p}_{y}}\} ,\quad {{p}_{x}} = - ({{{\mathbf{u}}}_{x}},{{\lambda }_{{{{{\mathbf{u}}}_{t}}}}}) - ({{{\mathbf{u}}}_{{xx}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}}) - ({{{\mathbf{u}}}_{{yx}}},{{\lambda }_{{{{{\mathbf{u}}}_{{yt}}}}}})\quad (x \leftrightarrow y)$
(2.4)
$\begin{gathered} {\mathbf{T}} = \left\| {\begin{array}{*{20}{c}} {{{T}_{{xx}}}}&{{{T}_{{xy}}}} \\ {{{T}_{{yx}}}}&{{{T}_{{yy}}}} \end{array}} \right\| \\ {{T}_{{xx}}} = \lambda - \left\{ {\left( {{{{\mathbf{u}}}_{x}},{{\lambda }_{{{{{\mathbf{u}}}_{x}}}}} - {{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}} - \frac{1}{2}{{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}} - {{\partial }_{t}}{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}}} \right) + ({{{\mathbf{u}}}_{{xx}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}}) + \frac{1}{2}({{{\mathbf{u}}}_{{xy}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}})} \right\} \\ {{T}_{{xy}}} = - \left\{ {\left( {{{{\mathbf{u}}}_{y}},{{\lambda }_{{{{{\mathbf{u}}}_{x}}}}} - {{\partial }_{x}}{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}} - \frac{1}{2}{{\partial }_{y}}{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}} - {{\partial }_{t}}{{\lambda }_{{{{{\mathbf{u}}}_{{xt}}}}}}} \right) + ({{{\mathbf{u}}}_{{xy}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xx}}}}}}) + \frac{1}{2}({{{\mathbf{u}}}_{{yy}}},{{\lambda }_{{{{{\mathbf{u}}}_{{xy}}}}}})} \right\} \\ (x \leftrightarrow y) \\ \end{gathered} $

Здесь $h$ – плотность функции Гамильтона, ${\mathbf{S}}$ – вектор плотности потока энергии (вектор Умова–Пойнтинга [5, 18]), ${\mathbf{p}}$ – вектор плотности волнового импульса, ${\mathbf{T}}$ – тензор плотности потока волнового импульса.

Плотность потока импульса через границы элемента двумерной системы есть не что иное, как плотность действующей на этот элемент силы, поэтому тензор (2.4) часто называют тензором напряжений [2, 19]. Справа в уравнении (2.1) стоит вектор плотности сил отдачи ${{{\mathbf{F}}}_{{\text{0}}}} = \{ {{\lambda }_{x}},{{\lambda }_{y}}\} $, возникающих из-за распределенного отражения волн при их распространении в неограниченной системе.

С целью получения уравнений переноса энергии и импульса вдоль движущегося одномерного объекта, умножим равенства (1.2) и (1.3) на соответствующие частные производные первого порядка обобщенных координат ${{{\mathbf{u}}}^{0}}(y,t)$, ${{{\mathbf{w}}}^{0}}(y,t)$, $\ell (y,t)$ и приведем их к виду

(2.5)
${{\partial }_{t}}{{h}^{0}} + {{\partial }_{y}}{{S}^{0}} = - ({\mathbf{u}}_{t}^{0},[{\mathbf{N}}] - {{{\mathbf{q}}}_{1}}) - ({\mathbf{w}}_{t}^{0},[{\mathbf{M}}] - {{{\mathbf{q}}}_{2}}) - {{\ell }_{t}}([F] - {{q}_{3}}) - {{L}_{t}}$
(2.6)
${{\partial }_{t}}{{p}^{0}} + {{\partial }_{y}}{{T}^{0}} = ({\mathbf{u}}_{y}^{0},[{\mathbf{N}}] - {{{\mathbf{q}}}_{1}}) + ({\mathbf{w}}_{y}^{0},[{\mathbf{M}}] - {{{\mathbf{q}}}_{2}}) + {{\ell }_{y}}([F] - {{q}_{3}}) + {{L}_{y}}$
${{h}^{0}} = ({\mathbf{u}}_{t}^{0},{{L}_{{{\mathbf{u}}_{t}^{0}}}}) + ({\mathbf{w}}_{t}^{0},{{L}_{{{\mathbf{w}}_{t}^{0}}}}) + {{\ell }_{t}}{{L}_{{{{\ell }_{t}}}}} + ({\mathbf{u}}_{{yt}}^{0},{{L}_{{{\mathbf{u}}_{{yt}}^{0}}}}) + ({\mathbf{w}}_{{yt}}^{0},{{L}_{{{\mathbf{w}}_{{yt}}^{0}}}}) + {{\ell }_{{yt}}}{{L}_{{{{\ell }_{{yt}}}}}} - L$
${{S}^{0}} = ({\mathbf{u}}_{t}^{0},{{L}_{{{\mathbf{u}}_{y}^{0}}}} - {{\partial }_{t}}{{L}_{{{\mathbf{u}}_{{yt}}^{0}}}} - {{\partial }_{y}}{{L}_{{{\mathbf{u}}_{{yy}}^{0}}}}) + ({\mathbf{w}}_{t}^{0},{{L}_{{{\mathbf{w}}_{y}^{0}}}} - {{\partial }_{t}}{{L}_{{{\mathbf{w}}_{{yt}}^{0}}}} - {{\partial }_{y}}{{L}_{{{\mathbf{w}}_{{yy}}^{0}}}}) + $
$ + \;{{\ell }_{t}}({{L}_{{{{\ell }_{y}}}}} - {{\partial }_{t}}{{L}_{{{{\ell }_{{yt}}}}}} - {{\partial }_{y}}{{L}_{{{{\ell }_{{yy}}}}}}) + ({\mathbf{u}}_{{yt}}^{0},{{L}_{{{\mathbf{u}}_{{yy}}^{0}}}}) + ({\mathbf{w}}_{{yt}}^{0},{{L}_{{{\mathbf{w}}_{{yy}}^{0}}}}) + {{\ell }_{{yt}}}{{L}_{{{{\ell }_{{yy}}}}}}$
${{p}^{0}} = - ({\mathbf{u}}_{y}^{0},{{L}_{{{\mathbf{u}}_{t}^{0}}}}) - ({\mathbf{w}}_{y}^{0},{{L}_{{{\mathbf{w}}_{t}^{0}}}}) - {{\ell }_{y}}{{L}_{{{{\ell }_{t}}}}} - ({\mathbf{u}}_{{yy}}^{0},{{L}_{{{\mathbf{u}}_{{yt}}^{0}}}}) - ({\mathbf{w}}_{{yy}}^{0},{{L}_{{{\mathbf{w}}_{{yt}}^{0}}}}) - {{\ell }_{{yy}}}{{L}_{{{{\ell }_{{yt}}}}}}$
${{T}^{0}} = L - ({\mathbf{u}}_{y}^{0},{{L}_{{{\mathbf{u}}_{y}^{0}}}} - {{\partial }_{t}}{{L}_{{{\mathbf{u}}_{{yt}}^{0}}}} - {{\partial }_{y}}{{L}_{{{\mathbf{u}}_{{yy}}^{0}}}}) - ({\mathbf{w}}_{y}^{0},{{L}_{{{\mathbf{w}}_{y}^{0}}}} - {{\partial }_{t}}{{L}_{{{\mathbf{w}}_{{yt}}^{0}}}} - {{\partial }_{y}}{{L}_{{{\mathbf{w}}_{{yy}}^{0}}}}) - $
$ - \;{{\ell }_{y}}({{L}_{{{{\ell }_{y}}}}} - {{\partial }_{t}}{{L}_{{{{\ell }_{{yt}}}}}} - {{\partial }_{y}}{{L}_{{{{\ell }_{{yy}}}}}}) - ({\mathbf{u}}_{{yy}}^{0},{{L}_{{{\mathbf{u}}_{{yy}}^{0}}}}) - ({\mathbf{w}}_{{yy}}^{0},{{L}_{{{\mathbf{w}}_{{yy}}^{0}}}}) - {{\ell }_{{yy}}}{{L}_{{{{\ell }_{{yy}}}}}}$

Здесь ${{h}^{0}}$ – плотность функции Гамильтона движущегося объекта, ${{S}^{0}}$ – плотность потока энергии, ${{p}^{0}}$ – плотность волнового импульса, ${{T}^{0}}$ – плотность потока волнового импульса, ${{L}_{t}}$ и ${{L}_{y}}$ – мощность источника, изменяющего параметры объекта, и плотность сил отдачи.

Уравнения (2.1) выражают собой локальные законы изменения энергии и волнового импульса в направляющей. Интегрируя эти уравнения по области

$\sigma = \{ (x,y){\text{:}}\;{{x}_{1}} \leqslant x \leqslant {{x}_{2}},0 \leqslant y \leqslant {{b}_{0}}\} $
которая разделена движущимся объектом на две, можно получить глобальные законы изменения энергии и импульса упругой полосы и отдельных ее частей. Для упругой полосы имеем
(2.7)
$\begin{gathered} \frac{{dH}}{{dt}} = - \oint\limits_\Gamma {{{S}_{n}}d\tau } + \int\limits_0^{{{b}_{0}}} {[{{{\mathbf{n}}}_{1}}{\mathbf{S}} - {{\ell }_{t}}h]dy} + \iint\limits_\sigma {\{ - {{\lambda }_{t}} + ({\mathbf{q}},{{{\mathbf{u}}}_{t}})\} dxdy};\quad H = \iint\limits_\sigma {hdxdy} \\ \frac{{d{\mathbf{P}}}}{{dt}} = - \oint\limits_\Gamma {{{T}_{n}}d\tau } + \int\limits_0^{{{b}_{0}}} {[{{{\mathbf{n}}}_{1}}{\mathbf{T}} - {{\ell }_{t}}{\mathbf{p}}]dy} + \iint\limits_\sigma {\{ {{{\mathbf{F}}}_{0}} - ({\mathbf{q}},grad{\mathbf{u}})\} dxdy};\quad {\mathbf{P}} = \iint\limits_\sigma {{\mathbf{p}}dxdy} \\ {{{\mathbf{n}}}_{1}} = (1, - {{\ell }_{y}}) \\ \end{gathered} $
где $\Gamma $ – граница области $\sigma $, нормальные составляющие отмечены индексом n.

Интегрируя уравнения (2.5) и (2.6) вдоль $y \in [0,{{b}_{0}}]$, находим уравнения изменения энергии и волнового импульса движущегося одномерного объекта

(2.8)
$\begin{gathered} \frac{{d{{H}^{0}}}}{{dt}} = - [{{S}^{0}}]_{0}^{{{{b}_{0}}}} - \int\limits_0^{{{b}_{0}}} {\{ ({\mathbf{u}}_{t}^{0},[{\mathbf{N}}] - {{{\mathbf{q}}}_{1}}) + ({\mathbf{w}}_{t}^{0},[{\mathbf{M}}] - {{{\mathbf{q}}}_{2}}) + {{\ell }_{t}}([F] - {{q}_{3}}) + {{L}_{t}}\} dy;\quad {{H}^{0}} = \int\limits_0^{{{b}_{0}}} {{{h}^{0}}dy} } \\ \frac{{d{{P}^{0}}}}{{dt}} = - [{{T}^{0}}]_{0}^{{{{b}_{0}}}} + \int\limits_0^{{{b}_{0}}} {\{ ({\mathbf{u}}_{y}^{0},[{\mathbf{N}}] - {{{\mathbf{q}}}_{1}}) + ({\mathbf{w}}_{y}^{0},[{\mathbf{M}}] - {{{\mathbf{q}}}_{2}}) + {{\ell }_{y}}([F] - {{q}_{3}}) + {{L}_{y}}\} dy} ;\quad {{P}^{0}} = \int\limits_0^{{{b}_{0}}} {{{p}^{0}}dy} \\ \end{gathered} $

Согласно формулам (2.7) и (2.8), изменение энергии всей сложной системы в целом “направляющая + движущийся объект” будет иметь вид

$\begin{gathered} \frac{{d(H + {{H}^{0}})}}{{dt}} = - [{{S}^{0}}]_{0}^{{{{b}_{0}}}} + \int\limits_0^{{{b}_{0}}} {\{ ({\mathbf{u}}_{t}^{0},{{{\mathbf{q}}}_{1}}) + ({\mathbf{w}}_{t}^{0},{{{\mathbf{q}}}_{2}}) + {{\ell }_{t}}{{q}_{3}} + {{L}_{t}}\} dy} - \\ - \;\oint\limits_\Gamma {{{S}_{n}}d\tau } + \iint\limits_\sigma {\{ - {{\lambda }_{t}} + ({\mathbf{q}},{{{\mathbf{u}}}_{t}})\} dxdy} \\ \end{gathered} $

Изменение полной энергии происходит за счет потока энергии через границы и работы как внешних сил, так и сил, изменяющих параметры системы.

При движении абсолютно жесткого закрепления, т.е. при

$u(\ell (y,t),y,t) = 0,\quad {{u}_{x}}(\ell (y,t),y,t) = 0$
компоненты вектора плотности потока энергии связаны с компонентами тензора плотности потока волнового импульса посредством соотношения
(2.9)
${{S}_{x}} - {{\ell }_{y}}{{S}_{y}} - {{\ell }_{t}}h = {{\ell }_{t}}({{T}_{{xx}}} - {{\ell }_{y}}{{T}_{{yx}}} - {{\ell }_{t}}{{p}_{x}}),$
которое выполняется на движущейся границе.

Для того чтобы выяснить влияние движения закрепления на энергию колебаний двумерной системы, закрепленную абсолютно жестко ($u = 0$, ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial {\mathbf{n}}}}} \right. \kern-0em} {\partial {\mathbf{n}}}} = 0$) по ограниченному контуру ($x = {{x}_{{1,2}}}$, $x = \ell (y,t)$, $y = 0$, $y = {{b}_{0}}$), будем полагать, что ее параметры постоянны (${{\lambda }_{t}} = 0$), а внешние силы отсутствуют (${\mathbf{q}} = 0$). Из формул (2.7) и (2.9) следует уравнение

(2.10)
$\frac{{dH}}{{dt}} = - \int\limits_0^{{{b}_{0}}} {{{\ell }_{t}}F} dy$

Известно [2, 5], что при движении границы со скоростью, меньшей скорости распространения волн, падающая волна всегда отталкивает границу. Следовательно, согласно уравнению (2.10), при уменьшении размеров двумерной системы энергия ее колебаний увеличивается (${{dH} \mathord{\left/ {\vphantom {{dH} {dt}}} \right. \kern-0em} {dt}} > 0$), а при увеличении уменьшается (${{dH} \mathord{\left/ {\vphantom {{dH} {dt}}} \right. \kern-0em} {dt}} < 0$).

Для двумерной системы, ограниченной двумя движущимися абсолютно жесткими закреплениями, имеем

(2.11)
$\frac{{dH}}{{dt}} = \int\limits_0^{{{b}_{0}}} {({{\ell }_{{1t}}}{{F}_{1}} - {{\ell }_{{2t}}}{{F}_{2}})} dy$
и можно, по-видимому, утверждать, что в случае движения границ со скоростями, меньшими скорости распространения волн, при сближении закреплений (${{\ell }_{{1t}}} > 0$, ${{\ell }_{{2t}}} < 0$) энергия колебаний возрастает $\left( {{{dH} \mathord{\left/ {\vphantom {{dH} {dt}}} \right. \kern-0em} {dt}} > 0} \right)$, а при удалении – уменьшается. В первом случае внешние силы, сдвигающие закрепления, совершают работу против сил давления волн и увеличивают энергию системы. Во втором – работа по раздвиганию закреплений совершается силами давления волн, и энергия отбирается у двумерной системы.

Работа выполнена при поддержке Российского научного фонда (14-19-01637).

Список литературы

  1. Болдин В.П., Весницкий А.И. Краевые задачи динамики двумерных упругих систем с движущимися нагрузками и закреплениями // Машиновед. 1989. № 1. С. 70–75.

  2. Болдин В.П., Маланов С.Б., Уткин Г.А. Постановка краевых задач динамики двумерных систем с движущимися нагрузками и закреплениями // ПММ. 1992. Т. 56. Вып. 1. С. 34–39.

  3. Весницкий А.И., Каплан Л.Э., Уткин Г.А. Вывод естественных граничных условий для одномерных задач динамики упругих систем с движущимися закреплениями и нагрузками // Дифф. интегр. уравн. 1982. Вып. 6. С. 75–80.

  4. Вибрации в технике. Т. 1. Колебания линейных систем / Под ред. В.В. Болотина. М.: Машиностр., 1999. 504 с.

  5. Весницкий А.И. Волны в системах с движущимися границами и нагрузками. М.: Физматлит, 2001. 320 с.

  6. Ерофеев В.И., Кажаев В.В., Семерикова Н.П. Волны в стержнях. Дисперсия. Диссипация. Нелинейность. М.: Физматлит, 2002. 208 с.

  7. Козин В.М., Жесткая В.Д., Погорелова А.В., Чижиумов С.Д., Джабраилов М.Р., Морозов В.С., Кустов А.Н. Прикладные задачи динамики ледяного покрова. М.: Изд. Акад. Естествозн., 2008. (URL: https://www.monographies.ru/ru/book/view?id=14)

  8. Весницкий А.И. Избранные труды по механике. Н. Новгород: Наш дом, 2010. 248 с.

  9. Altenbach H., Eremeyev V.A. (Eds). Shell-like Structures. Advanced Structured Materials. V. 15. B.; Heidelberg: Springer, 2011. 750 p.

  10. Коузов Д.П., Филиппенко Г.В. Колебания упругой пластины, частично погруженной в жидкость // ПММ. 2010. Т. 74. № 5. С. 864–878.

  11. Бутова С.В., Герасимов С.И., Ерофеев В.И., Камчатный В.Г. Устойчивость движения высокоскоростных объектов по направляющим ракетного трека // Пробл. машиностр. надежн. машин. 2015. № 1. С. 3–8.

  12. Герасимов С.И., Ерофеев В.И. Расчет изгибно-крутильных колебаний рельсовой направляющей ракетного трека // Пробл. машиностр. надежн. машин. 2016. № 3. С. 25–27.

  13. Ерофеев В., Потапов А., Солдатов И. Нелинейные волны в упругих системах. Saarbrücken: LAP LAMBERT Acad. Publish., 2015. 236 с.

  14. Tolstoy I., Usdin E. Wave propagation in elastic plates: low and high mode dispersion // J. Acoust. Soc. Amer. 1957. V. 29. № 1. P. 37–42.

  15. Гринченко В.Т., Мелешко В.В. Гармонические колебания и волны в упругих телах. Киев: Наук. думка, 1981. 284 с.

  16. Шевченко В.В. Прямые и обратные волны // УФН. 2007. Т. 177. № 3. С. 301–306.

  17. Lamb H. On group velocity // Proc. Lond. Math. Soc. Ser. 2. 1904. V. 1. № 849. P. 473–479.

  18. Ерофеев В.И., Лисенкова Е.Е. Общие соотношения для волн в одномерных упругих системах // ПММ. 2013. Т. 77. Вып. 2. С. 315–321.

  19. Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1988. 512 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал