Прикладная математика и механика, 2019, T. 83, № 1, стр. 47-62

КОНТАКТНАЯ ЗАДАЧА КАЧЕНИЯ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ВЯЗКОУПРУГОМУ ОСНОВАНИЮ ПРИ НАЛИЧИИ СЛОЯ ВЯЗКОЙ СМАЗКИ

П. П. Усов^*

Национальный исследовательский университет “Московский институт электронной техники”
Москва, Зеленоград, Россия

Поступила в редакцию 29.08.2016

DOI: 10.1134/S0032823519010120

Аннотация

На основании модели Кельвина вязкоупругой среды рассматривается стационарное движение тонкого слоя вязкой смазки между вязкоупругим цилиндром и вязкоупругим основанием. Исследуется влияние безразмерного параметра, пропорционального времени релаксации вязкоупругих тел, на характеристики слоя смазки. Показано, что при высоком значении этого параметра решение задачи о контакте вязкоупругих тел, разделенных тонким слоем смазки, близко к решению упругогидродинамической задачи в случае модуля упругости, равного мгновенному модулю упругости вязкоупругих тел. При уменьшении значения параметра область высокого давления расширяется, а максимальное давление падает, причем второй максимум давления убывает быстрее первого и исчезает. Показано, что коэффициент трения качения как функция времени релаксации имеет максимум. При малых значениях времени релаксации зазор на входе принимает форму, при которой режим обильной смазки оказывается невозможным. В результате толщина слоя смазки быстро уменьшается с уменьшением времени релаксации.

Ключевые слова: вязкоупругий цилиндр, качение, толщина слоя смазки, давление в слое смазки, коэффициент трения

При анализе процессов, протекающих в тонком слое смазки, разделяющем деформируемые поверхности, контактирующие тела обычно моделируют упругой средой [1–4], что не всегда оправданно. Во-первых, механические свойства поверхностных слоев контактирующих тел могут быть отличными от свойств основного материала и могут зависеть от скоростей относительных перемещений взаимодействующих тел. Во-вторых, в последнее время наметилась тенденция использования в узлах трения различных композиционных материалов, поверхностные слои которых обладают реологическими свойствами. В связи с этим практический интерес представляет исследование влияния неупругих свойств контактирующих тел на характеристики смазываемого контакта.

Ранее [5–7] в плоской постановке было исследовано влияние вязкоупругих свойств тонких покрытий на упругих цилиндрических телах, на характеристики смазываемого контакта и показано, что это влияние существенно. Результаты значительно отличаются от случая контакта однородных упругих тел при малых скоростях относительного движения тел. Максимум давления при наличии вязкоупругих покрытий ниже, точка максимума смещена в сторону входа, а размер области высокого давления больше. С ростом скорости движения коэффициент трения уменьшается, достигает минимального значения, а затем возрастает, влияние вязких свойств ослабевает. Когда время прохождения области контакта становится малым по сравнению со временем релаксации вязкоупругих покрытий, влияние вязких свойств становится несущественным.

Рассматривалась [8] задача о движении тонкого слоя вязкой смазки между поверхностями жесткой сферы и вязкоупругого слоя, сцепленного с жестким основанием. Исследовано влияние механических характеристик вязкоупругого слоя на распределение давления в слое смазки, его толщину и коэффициент трения. Показано отличие полученных результатов для вязкоупругого слоя от результатов в случае упругих тел.

Была рассмотрена [9] задача о смазываемом контакте жесткого цилиндра, поверхность которого имеет регулярный микрорельеф, и вязкоупругого слоя, движущегося относительно цилиндра с постоянной скоростью. Проведен анализ зависимости толщины слоя смазки, распределения давления в области контакта, а также силы трения от вязкоупругих характеристик поверхностного слоя и параметров рельефа.

В приведенных работах рассмотрен вопрос о влиянии вязкоупругих свойств тонких поверхностных слоев на характеристики смазываемых контактов. При этом для определения перемещений поверхности вязкоупругого слоя использовались одномерные модели. Рассмотренные модели имеют отношение к случаю, когда толщина покрытия с вязкоупругими свойствами значительно меньше ширины области контакта. Если толщина покрытия значительно больше размера области контакта, для определения перемещения поверхностей вязкоупругих тел могут быть использованы решения задач теории вязкоупругости для полупространства.

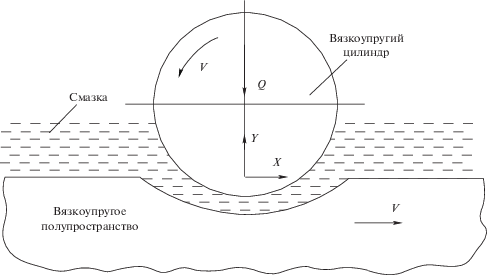
1. Постановка задачи. Рассмотрим задачу о движении тонкого слоя вязкой жидкости между вращающимся вязкоупругим цилиндром и подвижным вязкоупругим основанием (фиг. 1). Полагаем, что скорость поверхности цилиндра $V$ равна скорости движения основания, т.е. имеет место режим чистого качения. Полагаем также, что механические свойства цилиндра и основания одни и те же.

Фиг. 1

Считаем, что радиус цилиндра велик по сравнению с размером области контакта, и для определения перемещений поверхности цилиндра можно использовать решение задачи плоской теории вязкоупругости для полупространства.

Перемещение поверхности вязкоупругого основания также будем находить из решения плоской задачи для полупространства.

Введем систему координат $OXY$, в которой центр цилиндра покоится. Начало системы координат поместим на поверхности недеформированного основания в точке, через которую проходит линия действия нагрузки. Ось $X$ направим в сторону движения поверхностей, а ось $Y$ – по внешней нормали к поверхности основания.

В системе координат $OXY$ выражение для толщины слоя смазки с учетом деформаций контактирующих тел запишем в виде

(1.1)

$H(X) = {{H}_{c}} + \frac{{{{X}^{2}} - X_{c}^{2}}}{{2R}} - 2(U(X) - U({{X}_{c}})),\quad {{H}_{c}} = H({{X}_{c}}),$

где ${{X}_{c}}$ – координата выходной границы слоя смазки, $U(X)$ – перемещение по нормали вследствие деформаций контактирующих тел одной поверхности в точке с координатой $X$, $R$ – радиус цилиндра. Перемещение $U(X)$ считаем положительным, если оно направлено по внешней нормали к поверхности.

Рассматривая движение вязкой ньютоновской жидкости в узком зазоре, полагаем, что выполнены все допущения, какие делаются при выводе уравнения Рейнольдса

(1.2)

$\frac{\partial }{{\partial X}}\left( {\frac{{\rho {{H}^{3}}}}{{12\mu }}\frac{{\partial P}}{{\partial X}}} \right) - V\frac{{\partial \left( {\rho H} \right)}}{{\partial X}} = 0$

из уравнений Навье–Стокса [10]. Здесь $\rho $ и $\mu $ – плотность и вязкость смазки, $P$ – давление в слое смазки.

Зависимость плотности смазки от давления принимаем в виде [10]

(1.3)

$\rho = {{\rho }_{0}}\left( {1 + \frac{{{{C}_{1}}P}}{{1 + {{C}_{2}}P}}} \right)$

где ${{\rho }_{0}}$ – плотность смазки при атмосферном давлении, ${{C}_{1}}$ и ${{C}_{2}}$ – постоянные, типичные значения которых для минеральных масел [10]

${{C}_{1}} = 0.6 \times {{10}^{{ - 9}}}\;{\text{П }}{{{\text{а }}}^{{ - 1}}},\quad {{C}_{2}} = 1.7 \times {{10}^{{ - 9}}}\;{\text{П }}{{{\text{а }}}^{{ - 1}}}$

Для учета зависимости вязкости смазки от давления приемлема модель Баруса [10]

(1.4)

$\mu = {{\mu }_{0}}\exp \left( {{{\alpha }_{0}}P} \right),$

где ${{\mu }_{0}}$ – вязкость смазки при атмосферном давлении, ${{\alpha }_{0}}$ – пьезокоэффициент вязкости.

Толщина слоя смазки $H(X)$ и распределение давления в нем $P(X)$ определяют момент сил, действующих на цилиндр со стороны слоя смазки, и касательные силы, действующие на поверхности:

$M = \int\limits_A^{{{X}_{c}}} {XP(X)dX} ,\quad {{T}_{{{\text{up}}}}} = \int\limits_A^{{{X}_{c}}} {\frac{H}{2}\frac{{dP}}{{dX}}dX} ,\quad {{T}_{{{\text{down}}}}} = - \int\limits_A^{{{X}_{c}}} {\frac{H}{2}\frac{{dP}}{{dX}}dX} $

Здесь$A$ – координата входной граничной точки слоя смазки. В условиях обильной смазки при теоретических исследованиях полагают $A = - \infty $. При численном решении задачи значение $A$ ограничивают таким образом, чтобы увеличение модуля $A$ незначительно изменяло результаты расчетов. Из результатов расчетов следует, что в случае упругих тел значение $\left| A \right|$, в полтора раза превышающее размер области контакта при сухом контакте тел, обеспечивает высокую точность. При увеличении $\left| A \right|$ в десять раз численное значение любого параметра изменяется не более чем в третьей значащей цифре. В случае вязкоупругих тел значение $\left| A \right|$ необходимо увеличивать, так как график функции распределения давления расположен левее, чем в случае упругих тел. В этом случае при выборе значения $\left| A \right|$ используем критерий: при увеличении $\left| A \right|$ в десять раз численное значение любого параметра должно изменяться не более чем в третьей значащей цифре.

Функция $U(X)$ в уравнении (1.1) неизвестна. Она зависит от распределения давления по области контакта и может быть определена путем решения уравнений теории вязкоупругости. Эти уравнения должны быть записаны в системе координат, в которой среда неподвижна.

Введем систему координат ${{O}^{0}}{{X}^{0}}{{Y}^{0}}$, жестко связанную с основанием. Координаты в разных системах координат связаны соотношениями

${{X}^{0}} = X - Vt,\quad {{Y}^{0}} = Y$

В качестве реологической модели вязкоупругих тел используется модель Кельвина [7, 11], согласно которой соотношения между деформациями и напряжениями в системе координат ${{O}^{0}}{{X}^{0}}{{Y}^{0}}$ имеют вид (случай плоской деформации изотропного вязкоупругого тела)

${{\sigma }_{{{{x}^{0}}}}} + {{T}_{\sigma }}\frac{{\partial {{\sigma }_{{{{x}^{0}}}}}}}{{\partial t}} = \lambda \left( {{{\theta }_{{{{x}^{0}}{{y}^{0}}}}} + {{T}_{\varepsilon }}\frac{{\partial {{\theta }_{{{{x}^{0}}{{y}^{0}}}}}}}{{\partial t}}} \right) + 2\mu \left( {{{\varepsilon }_{{{{x}^{0}}}}} + {{T}_{\varepsilon }}\frac{{\partial {{\varepsilon }_{{{{x}^{0}}}}}}}{{\partial t}}} \right)\quad \left( {x \leftrightarrow y} \right)$

(1.5)

$\begin{gathered} {{\tau }_{{{{x}^{0}}{{y}^{0}}}}} + {{T}_{\sigma }}\frac{{\partial {{\tau }_{{{{x}^{0}}{{y}^{0}}}}}}}{{\partial t}} = 2\mu \left( {{{\gamma }_{{{{x}^{0}}{{y}^{0}}}}} + {{T}_{\varepsilon }}\frac{{\partial {{\gamma }_{{{{x}^{0}}{{y}^{0}}}}}}}{{\partial t}}} \right) \\ - \infty < {{X}^{0}} < + \infty ,\quad - {\kern 1pt} \infty < {{Y}^{0}} < 0,\quad t > 0,\quad \mu = \frac{E}{{2(1 + \nu )}},\quad \lambda = \frac{{E\nu }}{{(1 + \nu )(1 - 2\nu )}} \\ \end{gathered} $

${{\varepsilon }_{{{{x}^{0}}}}} = \frac{{\partial {{U}_{{{{x}^{0}}}}}}}{{\partial {{X}^{0}}}},\quad {{\varepsilon }_{{{{y}^{0}}}}} = \frac{{\partial {{U}_{{{{y}^{0}}}}}}}{{\partial {{Y}^{0}}}},\quad 2{{\gamma }_{{{{x}^{0}}{{y}^{0}}}}} = \frac{{\partial {{U}_{{{{x}^{0}}}}}}}{{\partial {{Y}^{0}}}} + \frac{{\partial {{U}_{{{{y}^{0}}}}}}}{{\partial {{X}^{0}}}},\quad {{\theta }_{{{{x}^{0}}{{y}^{0}}}}} = \frac{{\partial {{U}_{{{{x}^{0}}}}}}}{{\partial {{X}^{0}}}} + \frac{{\partial {{U}_{{{{y}^{0}}}}}}}{{\partial {{Y}^{0}}}}$

${{U}_{{{{x}^{0}}}}}$, ${{U}_{{{{y}^{0}}}}}$ – компоненты вектора перемещения точки $({{X}^{0}},{{Y}^{0}})$.

Параметр $E$ – длительный модуль упругости (используемый ниже параметр E_t = = $E{{T}_{\varepsilon }}{\text{/}}{{T}_{\sigma }}$ – мгновенный модуль упругости) [7, 11].

Рассматриваем установившийся режим, когда в системе координат $OXY$ центр цилиндра, а также область контакта неподвижны, а толщина слоя смазки и распределение давления в нем не меняются со временем, т.е. $U_{y}^{0}({{X}^{0}},{{Y}^{0}})$ = $U_{y}^{0}(X - Vt,Y)$ = = ${{U}_{y}}(X,Y)$ и т.д.

В системе координат $OXY$ уравнения (1.5) имеют вид

${{\sigma }_{x}} + {{T}_{\sigma }}V\frac{{\partial {{\sigma }_{x}}}}{{\partial X}} = \lambda \left( {{{\theta }_{{xy}}} + {{T}_{\varepsilon }}V\frac{{\partial {{\theta }_{{xy}}}}}{{\partial X}}} \right) + 2\mu \left( {{{\varepsilon }_{x}} + {{T}_{\varepsilon }}V\frac{{\partial {{\varepsilon }_{x}}}}{{\partial X}}} \right)\left( {x \leftrightarrow y} \right)$

${{\tau }_{{xy}}} + {{T}_{\sigma }}V\frac{{\partial {{\tau }_{{xy}}}}}{{\partial X}} = 2\mu \left( {{{\gamma }_{{xy}}} + {{T}_{\varepsilon }}V\frac{{\partial {{\gamma }_{{xy}}}}}{{\partial X}}} \right)$

(1.6)

$ - \infty < X < + \infty ,\quad - {\kern 1pt} \infty < Y < 0$

${{\sigma }_{x}} = {{\sigma }_{x}}(X,Y)(x,X \leftrightarrow y,Y),\quad {{\tau }_{{xy}}} = {{\tau }_{{xy}}}(X,Y),\quad {{\varepsilon }_{x}} = \frac{{\partial {{U}_{x}}}}{{\partial X}}(x,X \leftrightarrow y,Y)$

$2{{\gamma }_{{xy}}} = \frac{{\partial {{U}_{x}}}}{{\partial Y}} + \frac{{\partial {{U}_{y}}}}{{\partial X}},\quad {{\theta }_{{xy}}} = \frac{{\partial {{U}_{x}}}}{{\partial X}} + \frac{{\partial {{U}_{y}}}}{{\partial Y}},\quad {{U}_{x}} = {{U}_{x}}(X,Y),\quad {{U}_{y}} = {{U}_{y}}(X,Y)$

Следуя Л.А. Галину [11], введем новые переменные

$\sigma _{x}^{*} = {{\sigma }_{x}} + {{T}_{\sigma }}V\frac{{\partial {{\sigma }_{x}}}}{{\partial X}}(x,X \leftrightarrow y,Y),\quad \tau _{{xy}}^{*} = {{\tau }_{{xy}}} + {{T}_{\sigma }}V\frac{{\partial {{\tau }_{{xy}}}}}{{\partial X}}$

(1.7)

$U_{x}^{*} = {{U}_{x}} + {{T}_{\varepsilon }}V\frac{{\partial {{U}_{x}}}}{{\partial X}}(x,X \leftrightarrow y,Y)$

$\varepsilon _{x}^{*} = \frac{{\partial U_{x}^{*}}}{{\partial X}}(x,X \leftrightarrow y,Y),\quad 2\gamma _{{xy}}^{*} = \frac{{\partial U_{x}^{*}}}{{\partial Y}} + \frac{{\partial U_{y}^{*}}}{{\partial X}},\quad \theta _{{xy}}^{*} = \frac{{\partial U_{x}^{*}}}{{\partial X}} + \frac{{\partial U_{y}^{*}}}{{\partial Y}}$

Из уравнений (1.6) следует, что переменные $\varepsilon _{x}^{*}$, $\varepsilon _{y}^{*}$, $\gamma _{{xy}}^{*}$, $\sigma _{x}^{*}$, $\sigma _{y}^{*}$, $\tau _{{xy}}^{*}$ удовлетворяют уравнениям, эквивалентным уравнениям равновесия для изотропного упругого тела. Кроме того [11], эти переменные будут удовлетворять уравнениям, эквивалентным уравнениям совместности деформаций и закону Гука для изотропного упругого тела. В частности, величины $U_{x}^{*}$ и $U_{y}^{*}$ удовлетворяют уравнениям

(1.8)

$\Delta U_{x}^{*} = - \frac{{\lambda + \mu }}{\mu }\frac{{\partial \theta {\text{*}}}}{{\partial X}}\quad (x,X \leftrightarrow y,Y)$

Уравнения (1.8) определяют функции $U_{x}^{*}(X,Y)$, $U_{y}^{*}(X,Y)$ в области $ - \infty < X < + \infty $, $ - \infty < Y \leqslant 0$, если заданы граничные условия. Такими условиями на бесконечностях ($X = \pm \infty $, $Y = - \infty $) являются условия ограниченности функций $U_{x}^{*}$, $U_{y}^{*}$. На границе $Y = 0$ эти условия – следствие условий

(1.9)

${{\sigma }_{y}}(X,0) = - P(X),\quad {{\tau }_{{xy}}}(X,0) = 0,$

где $P(X)$ – приложенное к поверхности нормальное давление. Влиянием касательных напряжений, действующих со стороны слоя смазки на поверхности, на перемещение поверхностей пренебрегаем (допущение, применяемое в теории смазки).

Соотношения между напряжениями ${{\sigma }_{y}}(X,Y)$, ${{\tau }_{{xy}}}(X,Y)$ и функциями $U_{x}^{*}(X,Y)$, $U_{y}^{*}(X,Y)$ имеют вид

(1.10)

$\sigma _{y}^{*} = \left( {\lambda + 2\mu } \right)\frac{{\partial U_{y}^{*}}}{{\partial Y}} + \lambda \frac{{\partial U_{x}^{*}}}{{\partial X}} = {{\sigma }_{y}} + V{{T}_{\sigma }}\frac{{\partial {{\sigma }_{y}}}}{{\partial X}},\;\,\tau _{{xy}}^{*} = \mu \left( {\frac{{\partial U_{x}^{*}}}{{\partial Y}} + \frac{{\partial U_{y}^{*}}}{{\partial X}}} \right) = {{\tau }_{{xy}}} + V{{T}_{\sigma }}\frac{{\partial {{\tau }_{{xy}}}}}{{\partial X}}$

Из (1.9) и (1.10) следуют граничные условия

(1.11)

$Y = 0{\text{:}}\quad \left( {\lambda + 2\mu } \right)\frac{{\partial U_{y}^{*}}}{{\partial Y}} + \lambda \frac{{\partial U_{x}^{*}}}{{\partial X}} = - P(X) - V{{T}_{\sigma }}\frac{{dP(X)}}{{dX}},\quad \frac{{\partial U_{x}^{*}}}{{\partial Y}} + \frac{{\partial U_{y}^{*}}}{{\partial X}} = 0$

Уравнения (1.8) совместно с условиями (1.11) и условиями ограниченности решения однозначно определяют функции $U_{x}^{*}(X,Y)$, $U_{y}^{*}(X,Y)$. Определив эти функции из уравнений (1.7), можно определить функции ${{U}_{x}}(X,Y)$, ${{U}_{y}}(X,Y)$, после чего определить функцию $U(X) = {{U}_{y}}(X,0)$.

Пусть $b$ – полуширина площадки контакта упругих тел с модулем упругости ${{E}_{t}}$ и коэффициентом Пуассона $\nu $ при отсутствии смазки. Введем безразмерные переменные по формулам

$x = X{\text{/}}b\quad (x,X \leftrightarrow y,Y),\quad u_{x}^{*} = R{\text{'}}U_{x}^{*}{\text{/}}{{b}^{2}},\quad u_{x}^{*} = R{\text{'}}U_{x}^{*}{\text{/}}{{b}^{2}}\quad (x,X \leftrightarrow y,Y)$

$h = {{R{\text{'}}H} \mathord{\left/ {\vphantom {{R{\text{'}}H} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}},\quad \bar {\mu } = {\mu \mathord{\left/ {\vphantom {\mu {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}},\quad \bar {\rho } = {\rho \mathord{\left/ {\vphantom {\rho {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}},\quad p = {P \mathord{\left/ {\vphantom {P {{{P}_{g}}}}} \right. \kern-0em} {{{P}_{g}}}}$

где ${{P}_{g}} = \sqrt {\frac{{QE{\text{'}}}}{{2\pi R{\text{'}}}}} $, $b = \sqrt {8QR{\text{'/(}}\pi E_{t}^{'}{\text{)}}} $, $E_{t}^{'} = {{E}_{t}}{\text{/(}}1 - {{\nu }^{2}}{\text{)}}$.

$R{\text{'}} = {R \mathord{\left/ {\vphantom {R 2}} \right. \kern-0em} 2}$ – приведенный радиус, $Q$ – нагрузка на единицу длины цилиндра.

В безразмерных переменных уравнения (1.1)–(1.4), (1.7), (1.8) и условия (1.11) принимают вид

(1.12)

$h(x) = {{h}_{c}} + \frac{{{{x}^{2}} - {{c}^{2}}}}{2} - 2(u(x) - u(c))$

(1.13)

$\frac{\partial }{{\partial x}}\left( {\frac{{\bar {\rho }{{h}^{3}}}}{{\bar {\mu }}}\frac{{\partial p}}{{\partial x}}} \right) - S\frac{{\partial \left( {\bar {\rho }h} \right)}}{{\partial x}} = 0$

(1.14)

$\bar {\rho } = 1 + \frac{{{{K}_{1}}p}}{{1 + {{K}_{2}}p}},\quad \bar {\mu } = \exp ( - Gp)$

(1.15)

$u(x) = {{u}_{y}}(x,0),\quad u_{x}^{*} = {{u}_{x}} + {{\tau }_{\varepsilon }}\frac{{\partial {{u}_{x}}}}{{\partial x}}\quad (x \leftrightarrow y)$

(1.16)

$(m + 1)\frac{{{{\partial }^{2}}u_{x}^{*}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u_{x}^{*}}}{{\partial {{y}^{2}}}} = - m\frac{{{{\partial }^{2}}u_{y}^{*}}}{{\partial x\partial y}},\quad \frac{{{{\partial }^{2}}u_{y}^{*}}}{{\partial {{x}^{2}}}} + (m + 1)\frac{{{{\partial }^{2}}u_{y}^{*}}}{{\partial {{y}^{2}}}} = - m\frac{{{{\partial }^{2}}u_{x}^{*}}}{{\partial y\partial x}}$

(1.17)

$y = 0{\text{:}}\;(m + 1)\frac{{\partial u_{y}^{*}}}{{\partial y}} + (m - 1)\frac{{\partial u_{x}^{*}}}{{\partial x}} = - \frac{m}{{m + 1}}\left[ {p(x) + {{{\tau }}_{{\sigma }}}\frac{{dp}}{{dx}}} \right],\quad \frac{{\partial u_{x}^{*}}}{{\partial y}} + \frac{{\partial u_{y}^{*}}}{{\partial x}} = 0,$

где

$S = \frac{{3{{\pi }^{2}}{{\mu }_{0}}VRE_{t}^{'}}}{{4{{Q}^{2}}}},\quad G = {{\alpha }_{p}}{{P}_{g}},\quad {{K}_{1}} = {{C}_{1}}{{P}_{g}},\quad {{K}_{2}} = {{C}_{2}}{{P}_{g}},\quad m = \frac{{\lambda + \mu }}{\mu }$

${{\tau }_{\varepsilon }} = \frac{{V{{T}_{\varepsilon }}}}{b},\quad {{\tau }_{\sigma }} = \frac{{V{{T}_{\sigma }}}}{b},\quad c = \frac{{{{X}_{c}}}}{b}$

Чтобы выразить функцию $u(x)$ через функцию $p(x)$, надо решить систему уравнений (1.16) при условиях (1.17), временно считая функцию $p(x)$ известной. Будем искать решение в классе обобщенных функций [12], используя преобразование Фурье по переменной $x$. Пусть

(1.18)

$p(x) = \delta (x),$

где $\delta (x)$ – дельта-функция [12]. Решение задачи при давлении (1.18) будем обозначать нижним индексом $\delta $. Фурье-образы функций будем обозначать теми же символами, только волнистой чертой сверху, т.е.

$\tilde {u}(\alpha ,y) = {{F}_{x}}[u(x,y)](\alpha ,y),$

где ${{F}_{x}}[g(x)](\alpha )$ – Фурье-образ функции $g(x)$.

Применяя к уравнениям (1.16) и условиям (1.17) преобразование Фурье, получаем

(1.19)

$\begin{gathered} - {{\alpha }^{2}}(m + 1)\tilde {u}_{{x,\delta }}^{*}(\alpha ,y) + \frac{{{{d}^{2}}\tilde {u}_{{x,\delta }}^{*}(\alpha ,y)}}{{d{{y}^{2}}}} = i\alpha m\frac{{d\tilde {u}_{{y,\delta }}^{*}(\alpha ,y)}}{{dy}} \\ - {{\alpha }^{2}}\tilde {u}_{{y,\delta }}^{*}(\alpha ,y) + (m + 1)\frac{{{{d}^{2}}\tilde {u}_{{y,\delta }}^{*}(\alpha ,y)}}{{d{{y}^{2}}}} = i\alpha m\frac{{d\tilde {u}_{{x,\delta }}^{*}(\alpha ,y)}}{{dy}} \\ \end{gathered} $

(1.20)

$\begin{gathered} {{\left. {(m + 1)\frac{{d\tilde {u}_{{y,\delta }}^{*}(\alpha ,y)}}{{dy}}} \right|}_{{y = 0}}} - i\alpha (m - 1)\tilde {u}_{{x,\delta }}^{*}(\alpha ,0) = - (1 - i\alpha {{\tau }_{\sigma }}) \\ {{\left. {\frac{{d\tilde {u}_{{x,\delta }}^{*}}}{{dy}}} \right|}_{{y = 0}}} - i\alpha \tilde {u}_{{y,\delta }}^{*}(\alpha ,0) = 0 \\ \end{gathered} $

Из уравнений (1.19) следуют уравнения

(1.21)

${{\alpha }^{4}}\tilde {u}_{{x,\delta }}^{*} - 2{{\alpha }^{2}}\frac{{{{d}^{2}}\tilde {u}_{{x,\delta }}^{*}}}{{d{{y}^{2}}}} + \frac{{{{d}^{4}}\tilde {u}_{{x,\delta }}^{*}}}{{d{{y}^{4}}}} = 0,\quad \tilde {u}_{{y,\delta }}^{*} = i\frac{{2m + 1}}{{\alpha m}}\frac{{d\tilde {u}_{{x,\delta }}^{*}}}{{dy}} - i\frac{{m + 1}}{{{{\alpha }^{3}}m}}\frac{{{{d}^{3}}\tilde {u}_{{x,\delta }}^{*}}}{{d{{y}^{3}}}}$

Общее решение первого уравнения (1.21), ограниченное на бесконечности, имеет вид

(1.22)

$\tilde {u}_{{x,\delta }}^{*}(\alpha ,y) = {{C}_{1}}\exp (\left| \alpha \right|y) + {{C}_{2}}y\exp (\left| \alpha \right|y),$

где ${{C}_{1}}$ и ${{C}_{2}}$ – постоянные. Подставляя это решение во второе уравнение (1.21), получаем

(1.23)

$\tilde {u}_{{y,\delta }}^{*}(\alpha ,y) = i\frac{{\left| \alpha \right|}}{\alpha }\exp (\left| \alpha \right|y)({{C}_{1}} + {{C}_{2}}y) - i{{C}_{2}}\frac{1}{\alpha }\frac{{m + 2}}{m}\exp (\left| \alpha \right|y)$

Подставляя выражения (1.22) и (1.23) в граничные условия (1.20), находим

$2i\left( {\alpha {{C}_{1}} - \frac{{m + 1}}{m}\frac{{\left| \alpha \right|}}{\alpha }{{C}_{2}}} \right) = - (1 - i\alpha {{\tau }_{\sigma }}),\quad 2\left| \alpha \right|{{C}_{1}} - \frac{2}{m}{{C}_{2}} = 0$

откуда следует, что

$\tilde {u}_{{y,\delta }}^{*}(\alpha ,0) = - \frac{{m + 1}}{{2m}}\frac{1}{{\left| \alpha \right|}}(1 - i\alpha {{\tau }_{\sigma }})$

Подставляя это выражение в выражение

${{\tilde {u}}_{{y,\delta }}}(\alpha ,0) = \frac{{\tilde {u}_{{y,\delta }}^{*}(\alpha ,0)}}{{1 - i\alpha {{\tau }_{\varepsilon }}}}$

найденное из соотношения (1.15), получаем равенство

${{\tilde {u}}_{{y,\delta }}}(\alpha ,0) = \frac{1}{{2m}}\left( { - \frac{{m + 1}}{{\left| \alpha \right|}}} \right)\frac{{1 - i\alpha {{\tau }_{\sigma }}}}{{1 - i\alpha {{\tau }_{\varepsilon }}}} = - \frac{1}{{\left| \alpha \right|}}\left[ {1 - \frac{{{{\alpha }^{2}}{{\tau }_{\varepsilon }}({{\tau }_{\varepsilon }} - {{\tau }_{\sigma }})}}{{1 + {{\alpha }^{2}}{{\tau }_{\varepsilon }}^{2}}} + i\frac{{\alpha ({{\tau }_{\varepsilon }} - {{\tau }_{\sigma }})}}{{1 + {{\alpha }^{2}}{{\tau }_{\varepsilon }}^{2}}}} \right]$

Применяя к нему обратное преобразование Фурье и учитывая, что [12]

${{F}^{{ - 1}}}\left[ {\frac{1}{{\left| \alpha \right|}}} \right] = - \frac{1}{\pi }\ln \left| x \right| - \frac{C}{\pi },$

где $C$ – постоянная Эйлера, получаем после преобразований

${{u}_{{y,\delta }}}(x,0) = \frac{1}{\pi }\left[ {\ln \left| x \right| + \frac{C}{\pi } + \Psi (x)} \right];\quad \Psi (x) = ({{\tau }_{\varepsilon }} - {{\tau }_{\sigma }})\int\limits_0^\infty {\frac{{{{\tau }_{\varepsilon }}\alpha \cos \alpha x - \sin \alpha x}}{{1 + {{\alpha }^{2}}{{\tau }_{\varepsilon }}^{2}}}} d\alpha $

Если нормальное давление распределено по поверхности, то для ее перемещения получаем выражение

$u(x) + \tilde {C} = \frac{1}{\pi }\int\limits_{ - \infty }^{ + \infty } {p(\xi )[\ln \left| {x - \xi } \right| + \Psi (x - \xi )]} d\xi ,\quad \tilde {C} = {\text{const}}$

Используя значения интегралов ([13], с. 420 и 421, формулы 3.723.1 и 3.723.5), выражение для функции $\Psi \left( x \right)$ можно привести к следующему:

$\Psi (x) = - \left( {1 - \frac{1}{\varsigma }} \right)\exp \left( { - \frac{x}{{{{\tau }_{\varepsilon }}}}} \right){{E}_{i}}\left( {\frac{x}{{{{\tau }_{\varepsilon }}}}} \right);\quad \varsigma = \frac{{{{\tau }_{\varepsilon }}}}{{{{\tau }_{\sigma }}}} = \frac{{{{T}_{\varepsilon }}}}{{{{T}_{\sigma }}}},\quad {{E}_{i}}(x) = \int\limits_{ - \infty }^x {\frac{{\exp (t)}}{t}dt} ,\quad x < 0$

В результате уравнение (1.12) принимает вид

(1.24)

$h(x) = {{h}_{c}} + \frac{{{{x}^{2}} - {{c}^{2}}}}{2} - \frac{\zeta }{\pi }\int\limits_a^c {p(\xi )\left[ {\ln \left| {\frac{{x - \xi }}{{c - \xi }}} \right| + \Psi (x - \xi ) - \Psi (c - \xi )} \right]} d\xi ;\quad a = \frac{A}{b}$

Функция $p(x)$ должна удовлетворять условиям

(1.25)

$p(a) = 0,\quad p(c) = 0,\quad {{\left. {\frac{{dp}}{{dx}}} \right|}_{{x = c}}} = 0$

используемым в теории смазки. Условие равновесия вала в безразмерных переменных имеет вид

(1.26)

$\int\limits_a^c {p(x)} dx = \frac{\pi }{2}$

Уравнения (1.13), (1.14), (1.24) и условия (1.25), (1.26) определяют координату точки обрыва слоя смазки $c$ и функции $h(x)$ и $p(x)$, если заданы значения входных параметров $a$, $S$, $G$, ${{K}_{1}}$, ${{K}_{2}}$, ${{\tau }_{\varepsilon }}$, $\zeta $.

После решения этой системы уравнений деформационную составляющую коэффициента трения ${{f}_{r}}$ и составляющую ${{f}_{t}}$, обусловленную сдвиговыми напряжениями, определяем по формулам

${{f}_{r}} = - \frac{M}{{QR}} = \frac{2}{{\pi }}\frac{b}{{R{\text{'}}}}{{\bar {f}}_{r}},\quad {{f}_{t}} = \frac{{{{T}_{{{\text{up}}}}}}}{Q} = \frac{2}{{\pi }}\frac{b}{{R{\text{'}}}}{{\bar {f}}_{t}};\quad {{\bar {f}}_{r}} = - \int\limits_a^c {xp(x)dx} ,\quad {{\bar {f}}_{t}} = \int\limits_a^c {\frac{h}{2}\frac{{dp}}{{dx}}} dx$

($f = {{f}_{r}} + {{f}_{t}}$ – коэффициент трения).

Проинтегрируем уравнение (1.13), учитывая правое граничное условие (1.25). В результате получим

(1.27)

$\bar {\rho }{{h}^{3}}\exp ( - Gp)\frac{{dp}}{{dx}} - S\bar {\rho }h = - S{{h}_{c}}$

2. Метод решения задачи. Введем на отрезке $[a,c]$ неравномерную сетку $\{ {{x}_{k}}\} $, k = = $0,1 \ldots ,N$, ${{x}_{0}} = a$, ${{x}_{N}} = c$.

В случае смазываемого контакта упругих тел в окрестности выходной граничной точки области контакта может иметь место второй максимум давления. При его наличии функция $p(x)$ быстро изменяется в окрестности этой точки. В то же время, во входной области функция $p(x)$ – монотонно возрастающая, и в малом шаге сетки здесь необходимости нет. Поэтому целесообразно разбиение области контакта по закону

${{x}_{0}} = a,\quad {{x}_{k}} - {{x}_{{k - 1}}} = \frac{{(1 - q){{q}^{{k - 1}}}}}{{1 - {{q}^{N}}}}(c - a),\quad k = 1,2,\; \ldots ,\;N,$

где $q < 1$. Число $q$ определяет степень уменьшения шага сетки при движении от входа к выходу. Например, при $N = 300$ и $q = 0.992$ получаем

${{x}_{1}} - {{x}_{0}} = 0.0088(c - a),\quad {{x}_{{300}}} - {{x}_{{299}}} = 0.0008(c - a)$

Число $q$ также является входным параметром.

Проинтегрируем уравнение (1.27) на интервале $({{x}_{k}},{{x}_{{k + 1}}})$, $k = 0,1, \ldots ,N - 1$. При вычислении интеграла функции $h(x)$ аппроксимируем ее на этом интервале линейной функцией, а при вычислении интеграла первого члена в левой части уравнения (1.27) воспользуемся приближенной формулой

$\begin{gathered} \int\limits_{{{x}_{k}}}^{{{x}_{{k + 1}}}} {\left[ {\bar {\rho }{{h}^{3}}\exp ( - Gp)\frac{{dp}}{{dx}}} \right]} dx = - \frac{1}{G}\int\limits_{{{x}_{k}}}^{{{x}_{{k + 1}}}} {\bar {\rho }{{h}^{3}}d\exp ( - Gp)} = \\ = \frac{1}{G}{{{\bar {\rho }}}_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}h_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{3}[\exp ( - G{{p}_{k}}) - \exp ( - G{{p}_{{k + 1}}})], \\ \end{gathered} $

где

${{p}_{k}} = p({{x}_{k}}),\quad {{h}_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{1}{2}({{h}_{k}} + {{h}_{{k + 1}}}),\quad {{\bar {\rho }}_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{1}{2}({{\bar {\rho }}_{k}} + {{\bar {\rho }}_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}),\quad {{h}_{k}} = h({{x}_{k}}),\quad {{\bar {\rho }}_{k}} = \bar {\rho }({{x}_{k}})$

После интегрирования получаем

(2.1)

$\begin{gathered} \frac{1}{G}{{{\bar {\rho }}}_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}h_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{3}[\exp ( - G{{p}_{k}}) - \exp ( - G{{p}_{{k + 1}}})] \\ - \;\frac{1}{2}S({{x}_{{k + 1}}} - {{x}_{k}})({{{\bar {\rho }}}_{k}}{{h}_{k}} + {{{\bar {\rho }}}_{{k + 1}}}{{h}_{{k + 1}}}) = - S{{h}_{c}}({{x}_{{k + 1}}} - {{x}_{k}}), \\ k = 0,1, \ldots ,N - 1 \\ \end{gathered} $

При вычислении интеграла в левой части равенства (1.26) функцию $p(x)$ заменяем сплайн-функцией первого порядка:

$p(x) = \sum\limits_{r = 0}^N {{{p}_{r}}} {{\nu }_{r}}(x),$

где ${{\nu }_{r}}(x)$ – линейная функция, ${{\nu }_{r}}(x) = 1$, если $x = {{x}_{r}}$ и ${{\nu }_{r}}(x) = 0$, если $x = {{x}_{i}}$, $i \ne r$. Принимая в равенстве (1.24) $x = {{x}_{k}}$ и интегрируя, получаем

(2.2)

${{h}_{k}} = {{h}_{c}} + \frac{{{{x}_{k}}^{2} - {{c}^{2}}}}{2} + \frac{\zeta }{\pi }\sum\limits_{j = 0}^N {{{p}_{j}}[{{g}_{j}}({{x}_{k}}) - {{g}_{j}}(c)]} ,\quad k = 0,1,\; \ldots ,\;N,$

где

${{g}_{j}}(x) = A_{j}^{1}(x) + A_{j}^{2}(x) + B_{j}^{1}(x) + B_{j}^{2}(x),\quad j = 0,1,\; \ldots ,\;N$

$A_{0}^{1}(x) = 0,\quad B_{N}^{2}(x) = 0$

$A_{j}^{1}(x) = {{[{{F}_{2}}(x)]}_{j}},\quad j = 1, \ldots ,N;\quad A_{j}^{2}(x) = (x - {{x}_{{j - 1}}}){{[{{F}_{1}}(x)]}_{j}},\quad j = 0,1, \ldots ,N$

$B_{j}^{1}(x) = ({{x}_{{j + 1}}} - x){{[{{F}_{1}}(x)]}_{{j + 1}}},\quad j = 0,1, \ldots ,N;$

$B_{j}^{2}(x) = - {{[{{F}_{2}}(x)]}_{{j + 1}}},\quad j = 0,1, \ldots ,N - 1$

${{[{{F}_{l}}(x)]}_{j}} = \frac{1}{{{{x}_{j}} - {{x}_{{j - 1}}}}}[{{F}_{l}}({{x}_{j}} - x) - {{F}_{l}}({{x}_{{j - 1}}} - x)],\quad l = 1,2$

${{F}_{1}}(x) = x(\ln \left| x \right| - 1) + \int {\Psi (x)dx} ,\quad {{F}_{2}}(x) = \frac{1}{2}{{x}^{2}}\left( {\ln \left| x \right| - \frac{1}{2}} \right) + \int {x\Psi (x)} dx$

При вычислении интегралов функции $\Psi (x)$ представим функцию ${{E}_{i}}(x)$ в виде степенного ряда [13]

${{E}_{i}}(x) = C + \ln \left| x \right| + \sum\limits_{k = 1}^\infty {\frac{{{{x}^{k}}}}{{kk!}}} {\kern 1pt} {\kern 1pt} ,$

где $C$ – постоянная Эйлера. После интегрирования получаем

$\int {\Psi (x)dx} = - {{\tau }_{\varepsilon }}(\zeta - 1)\left[ {\ln \left| {\tilde {x}} \right|(1 - \exp ( - \tilde {x})) - \exp ( - \tilde {x})\left( {C + \sum\limits_{k = 1}^\infty {{{{\tilde {x}}}^{k}}\frac{1}{{kk!}}} } \right)} \right]$

$\int {x\Psi (x)dx} = - \tau _{\varepsilon }^{2}(\zeta - 1)\left\{ {\tilde {x} + \ln \left| {\tilde {x}} \right|[1 - (1 + \tilde {x})\exp ( - \tilde {x})]{{ - }^{{^{{^{{^{{}}}}}}}}}} \right.$

$\left. { - \;(1 + \tilde {x})\exp ( - \tilde {x})\left( {C + \sum\limits_{k = 1}^\infty {{{{\tilde {x}}}^{k}}\frac{1}{{kk!}}} } \right)} \right\};$

$\tilde {x} = \frac{x}{{{{\tau }_{\varepsilon }}}}$

Граничные условия (1.25) в конечных разностях имеют вид

(2.3)

${{p}_{0}} = 0,\quad {{p}_{N}} = 0,\quad {{p}_{{N - 1}}} = 0$

Заменяя в условии (1.26) интеграл конечной суммой, получаем

(2.4)

$\sum\limits_{k = 1}^{N - 1} {{{p}_{k}}} ({{x}_{{k + 1}}} - {{x}_{{k - 1}}}) = \pi $

Принимая в первом уравнении (1.14) $x = {{x}_{k}}$, получаем

(2.5)

${{\bar {\rho }}_{k}} = 1 + \frac{{{{K}_{1}}{{p}_{k}}}}{{1 + K{}_{2}{{p}_{k}}}},\quad k = 0,\; \ldots ,\;N$

Уравнения (2.1)–(2.5) представляют собой систему нелинейных алгебраических уравнений, которая решается методом Ньютона.

3. Анализ результатов. Ниже приведены результаты расчетов при значениях параметров

$a = - 8.5,\quad S = 0.25,\quad G = 7,\quad {{K}_{1}} = 0.6,\quad {{K}_{2}} = 1.7,\quad \varsigma = 3,\quad N = 1200$

и разных значениях параметра ${{\tau }_{{\varepsilon }}}$, т.е. все параметры смазки, скорость качения и все параметры вязкоупругих тел, кроме времен релаксации ${{T}_{\varepsilon }}$ и ${{T}_{\sigma }}$, остаются неизменными, а времена релаксации ${{T}_{\varepsilon }}$ и ${{T}_{\sigma }}$ изменяются таким образом, что их отношение остается постоянным. Это означает, что как длительный, так и мгновенный модули упругости вязкоупругих тел не изменяются.

Параметр ${{\tau }_{\varepsilon }}$ равен отношению времени релаксации ${{T}_{\varepsilon }}$ к времени, за которое точка поверхности, двигаясь со скоростью $V$, пройдет расстояние $b$. До входа в область высокого давления поверхности цилиндров не нагружены, а после входа давление на поверхности цилиндров быстро возрастает, и деформации поверхностей происходят при модуле упругости, близком к мгновенному модулю. Если значение ${{\tau }_{\varepsilon }}$ велико, то точка поверхности пройдет область контакта за малую часть времени релаксации. За это время релаксации деформаций незначительны и модуль упругости остается высоким в течение всего процесса. Поэтому значению ${{\tau }_{\varepsilon }} = \infty $ соответствует случай упругогидродинамического контакта цилиндров при модуле упругости, равном мгновенному модулю упругости вязкоупругой среды.

При невысоких значениях параметра ${{\tau }_{\varepsilon }}$ в течение времени прохождения некоторой точки поверхности через область контакта податливость поверхности в этой точке постоянно изменяется, причем в данный момент времени она зависит от давления, которое действовало в данной точке в предыдущие моменты времени. Это приводит к тому, что распределение давления по области контакта в случае вязкоупругих тел отличается от распределения в случае упругих тел.

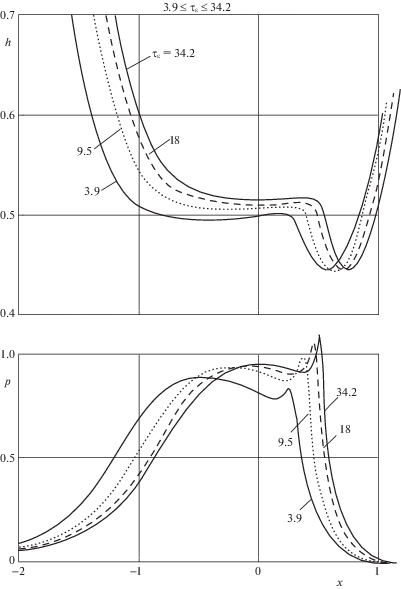
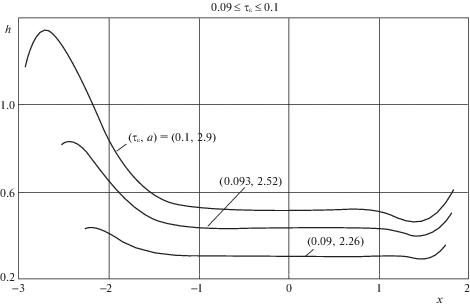
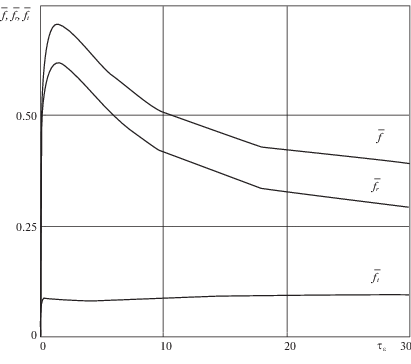
Изменения распределения давления, толщины слоя смазки и коэффициентов ${{\bar {f}}_{r}}$, ${{\bar {f}}_{t}}$ и $\bar {f} = (2b{\text{/}}\pi R{\text{'}})f$ по мере уменьшения параметра ${{\tau }_{\varepsilon }}$ от высокого до малого значения иллюстрируются результатами, приведенными на фиг. 2–5 при $0.09 \leqslant {{\tau }_{\varepsilon }} \leqslant 34.2$. При ${{\tau }_{\varepsilon }} = 34.2$ решение рассматриваемой задачи менее чем на один процент отличается от решения задачи для упругих тел. Значение ${{\tau }_{\varepsilon }} = 0.09$ – предельное, ниже которого смазываемый контакт переходит в сухой контакт. Чтобы наглядно продемонстрировать изменения функций $h(x)$ и $p(x)$ при уменьшении ${{\tau }_{\varepsilon }}$ до минимального значения весь интервал изменения ${{\tau }_{\varepsilon }}$ разбит на четыре интервала: $3.9 \leqslant {{\tau }_{\varepsilon }} \leqslant 34.2$ (фиг. 2), $0.2 \leqslant {{\tau }_{\varepsilon }} \leqslant 3.9$ (фиг. 3), $0.1 \leqslant {{\tau }_{\varepsilon }} \leqslant 0.2$, (фиг. 4), $0.09 \leqslant {{\tau }_{\varepsilon }} \leqslant 0.1$ (фиг. 5). В каждом из представленных интервалов имеются характерные особенности изменения решения с изменением параметра ${{\tau }_{\varepsilon }}$. В интервале $3.9 \leqslant {{\tau }_{\varepsilon }} \leqslant 34.2$ функция $p(x)$ имеет два максимума, в интервале $0.2 \leqslant {{\tau }_{\varepsilon }} \leqslant 3.9$ второй максимум исчезает и выходная граница смещается вправо, в интервале $0.1 \leqslant {{\tau }_{\varepsilon }} \leqslant 0.2$ на входе имеется область, в которой функция $h(x)$ возрастает и которая смещается вправо, в интервале $0.09 \leqslant {{\tau }_{\varepsilon }} \leqslant 0.1$ происходит быстрое падение толщины слоя смазки. На фиг. 6 приведены зависимости ${{\bar {f}}_{r}}$, ${{\bar {f}}_{t}}$ и $\bar {f}$ от ${{\tau }_{\varepsilon }}$ в интервале $0.09 \leqslant {{\tau }_{\varepsilon }} \leqslant 30$.

Фиг. 2

Фиг. 3

Фиг. 4

Фиг. 5

Фиг. 6

При ${{\tau }_{\varepsilon }} = 34.2$ (фиг. 2) решение задачи близко к решению упругогидродинамической задачи при мгновенном модуле упругости. Функция $p\left( x \right)$ при этом имеет высокий второй максимум давления. При уменьшении ${{\tau }_{\varepsilon }}$ область высокого давления сдвигается влево, к входной границе слоя смазки, а размер этой области слабо возрастает, причем оба максимума давления понижаются и сдвигаются влево. Второй (правый) максимум давления понижается быстрее, чем первый (левый), и при значении ${{\tau }_{\varepsilon }} = 3.9$ он становится ниже первого.

График толщины слоя смазки (верхняя часть фиг. 2) сдвигается влево вместе с областью высокого давления, при этом толщина слоя смазки в области высокого давления слабо убывает. Вследствие смещения графика функции $p(x)$ влево растет его асимметрия относительно линии действия нагрузки. Это приводит к росту ${{\bar {f}}_{r}}$, что подтверждают результаты, приведенные на фиг. 6, из которых следует, что коэффициент ${{\bar {f}}_{r}}$ растет при уменьшении ${{\tau }_{\varepsilon }}$ от значения 30 до значения 1.4.

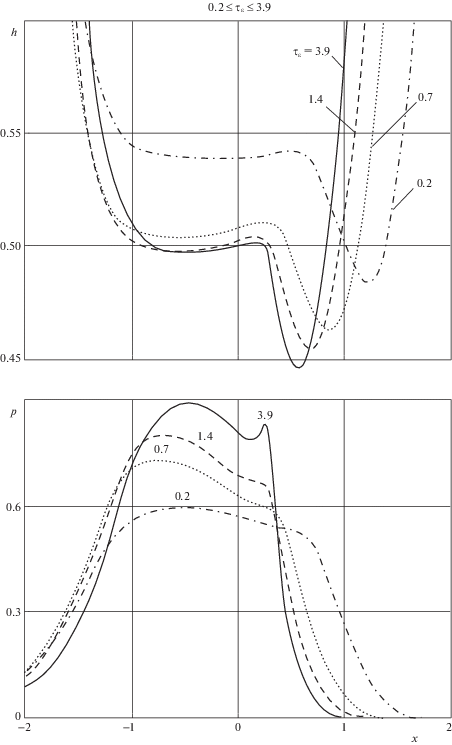
При изменении ${{\tau }_{\varepsilon }}$ от значения 3.9 до 1.4 (фиг. 3) область высокого давления расширяется, в основном влево. При этом асимметрия графика функции $p(x)$ относительно линии действия нагрузки возрастает, коэффициент ${{\bar {f}}_{r}}$ также возрастает. При дальнейшем уменьшении параметра ${{\tau }_{\varepsilon }}$ область высокого давления расширяется только вправо, график функции становится более симметричным и коэффициент ${{\bar {f}}_{r}}$ падает. В результате функция ${{\bar {f}}_{r}}({{\tau }_{\varepsilon }})$ имеет максимум при ${{\tau }_{\varepsilon }} = 1.4$.

Существенный рост размера области высокого давления при изменении параметра ${{\tau }_{\varepsilon }}$ от значения 1.4 до 0.2 приводит к небольшому росту толщины слоя смазки, что следует из результатов, приведенных на фиг. 3.

Дальнейшее поведение функций $h(x)$ и $p(x)$ при уменьшении ${{\tau }_{\varepsilon }}$ от значения 0.2 обусловлено изменением формы зазора до входа в область, в которой развивается высокое давление. Смещение области высокого давления влево приводит к увеличению расстояния между поверхностями на входе в область высокого давления. В результате при значении ${{\tau }_{\varepsilon }} = 0.2$ толщина слоя смазки является возрастающей в некоторой окрестности точки $x = a$, что следует из результатов, приведенных на фиг. 4.

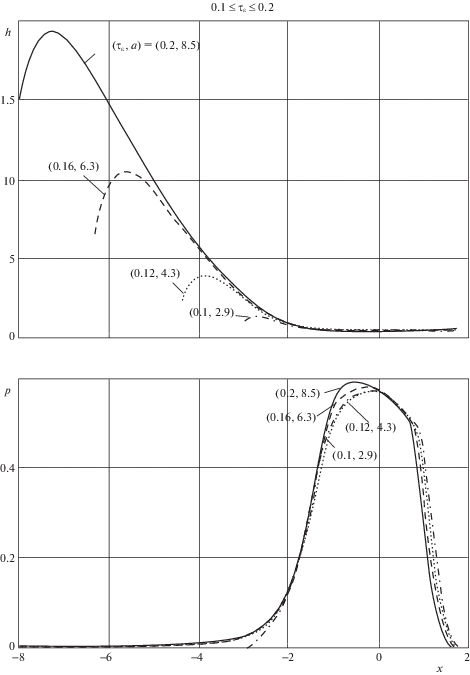
Чтобы между контактирующими телами образовался слой смазки, зазор между ними должен удовлетворять определенным требованиям, основным из которых является требование сужения зазора. Смещение области высокого давления влево приводит к тому, что при значениях ${{\tau }_{\varepsilon }} < 0.2$ слой смазки не может формироваться при значении входной координаты $a = 8.5$. Однако слой смазки может формироваться, если входная координата смещается вправо. На фиг. 4 для каждого значения ${{\tau }_{\varepsilon }}$ указано максимальное значение входной координаты $a$, при которой получено решение задачи.

Из результатов, приведенных на фиг. 4, следует, что при изменении ${{\tau }_{\varepsilon }}$ от значения 0.2 до 0.1 толщина слоя смазки в области высокого давления изменяется слабо. Функция $p(x)$ также изменяется слабо, но она становится более симметричной относительно линии действия нагрузки и коэффициент ${{\bar {f}}_{r}}$ продолжает падать (фиг. 6).

Дальнейшее уменьшение параметра ${{\tau }_{\varepsilon }}$ от значения ${{\tau }_{\varepsilon }} = 0.1$ приводит к дальнейшему сдвигу левой граничной точки слоя смазки вправо. При этом толщина слоя смазки в области высокого давления быстро падает. Это следует из результатов, приведенных на фиг. 5.

Быстрое падение толщины слоя смазки при уменьшении параметра ${{\tau }_{\varepsilon }}$ от значения 0.1 можно объяснить следующим образом. В УГД контакте в условиях обильной смазки давление начинает заметно возрастать на большом расстоянии от области, в которой развивается высокое давление. В случае контакта вязкоупругих тел, когда время релаксации мало, давление не может возрастать на большом расстоянии от области высокого давления. Этому препятствуют деформации тел. В результате область, в которой начинает развиваться давление, смещается вправо. В УГД контакте такая ситуация имеет место, когда смазка поступает в зазор в недостаточном количестве, чтобы обеспечить режим обильной смазки. При этом толщина слоя смазки падает из-за недостатка смазки. Уменьшение координаты $a$ в контакте вязкоупругих тел эквивалентно уменьшению количества смазки, подаваемой в зазор, и приводит к падению толщины слоя смазки.

Результаты расчетов, приведенные на фиг. 6, свидетельствуют о том, что значение коэффициента ${{f}_{t}}$ слабо зависит от параметра ${{\tau }_{\varepsilon }}$. Коэффициент трения $f$, также как и ${{f}_{r}}$ имеет максимум.

Список литературы

Kudish II. Elastohydrodynamic lubrication for line and point contacts. Asymptotic and numerical approaches. Boca Raton, FL: CRC Press, 2013. 672 p.
Usov P.P. Effects of lubricant viscoelasticity on film thickness in elastohydrodynamic line contacts during start-up // Proc. IMechE. Part J: J. Engng. Tribol. 2016. V. 230. № 7. P. 769–782.
Usov P.P. EHD effects in lubricated journal bearing // Lubricants. 2018. V. 6. № 12. P. 1–16.
Усов П.П. Численный анализ характеристик слоя смазки в опорном подшипнике скольжения при реверсивном движении // ПММ. 2018. Т. 82. Вып. 3. С. 1–11.
Kalker J.J. Viscoelastic multilayered cylinders rolling with dry friction // J. Appl. Mech. 1991. V. 58. P. 666–679.
Goryacheva I.G., Sadeghi F., Xu G. Viscoelastic effects in lubricated contacts // Wear. 1996. V. 198. P. 307–312.
Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.
Горячева И.Г., Усов П.П. Численный анализ вязкоупруго-гидродинамического точечного контакта при стационарных условиях // Трение и износ. 2010. Т. 31. № 1. С. 1–10.
Горячева И.Г., Усов П.П. Численный анализ контакта вязкоупругих шероховатых тел при наличии слоя вязкой смазки // ПММ. 2012. Т. 76. Вып. 5. С. 766–778.
Dowson D., Higginson G.R. Elastohydrodynamic Lubrication. The Fundamentals of Roller and Gear Lubrication. Oxford: Permagon, 1966.
Галин Л.А. Контактные задачи теории упругости и вязкоупругости. М.: Гл. ред. физ.-мат. лит., 1980. 302 с.
Владимиров В.С. Уравнения математической физики. М.: Гл. ред. физ.-мат. лит., 1967. 436 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Гос. изд. физ.-мат. лит., 1962. 1100 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал