Прикладная математика и механика, 2019, T. 83, № 1, стр. 107-125

МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКОГО ИЗГИБА ЖЕСТКОПЛАСТИЧЕСКИХ ГИБРИДНЫХ КОМПОЗИТНЫХ КРИВОЛИНЕЙНЫХ ПЛАСТИН С ЖЕСТКОЙ ВСТАВКОЙ

Т. П. Романова^*

Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Новосибирск, Россия

Поступила в редакцию 11.07.2017

DOI: 10.1134/S0032823519010107

Аннотация

Разработан общий метод расчета динамического поведения жесткопластических композитных слоисто-волокнистых тонких пластин с жесткой вставкой и с шарнирно опертым или защемленным произвольным гладким невогнутым криволинейным контуром, на которые действует равномерно распределенная по поверхности кратковременная динамическая нагрузка высокой интенсивности взрывного типа. Распределение слоев симметрично относительно срединной поверхности, в каждом слое находится семейство армирующих криволинейных волокон в направлениях, параллельных и нормальных к контуру пластины. Используется структурная модель армированного слоя с одномерным напряженным состоянием в волокнах. В зависимости от амплитуды нагрузки возможны разные механизмы деформирования пластин. На основе принципа виртуальной мощности в сочетании с принципом Даламбера для каждого из механизмов получены уравнения динамического деформирования и проанализированы условия их реализации. Получены аналитические выражения для оценки предельных нагрузок, времени деформирования и остаточных прогибов пластин. Показано, что изменение параметров армирования существенно влияет как на несущую способность таких пластин, так и на остаточные прогибы. Приведены примеры численных решений.

При воздействии высокоинтенсивных нагрузок на элементы конструкций их материалы проявляют в основном пластические свойства. Анализ литературных источников показывает, что исследования динамического деформирования композитных элементов конструкций за пределом упругого поведения находятся пока в зачаточном состоянии и для плоских элементов они затрагивают только круглые, кольцевые и прямоугольные пластины [1–8]. Для решения динамических задач при взрывном типе нагрузок широкое распространение получила модель жесткопластического тела [1, 9], благодаря ее простоте и удобству расчетных схем. Обсуждалось современное состояние расчетов неупругого динамического деформирования оболочечных конструкций слоисто-волокнистой структуры и приведено обоснование использования модели жесткопластического тела в таких задачах, а также рассмотрены [1] достоинства и недостатки структурной модели армированного слоя с одномерным напряженным состоянием в волокнах [10, 11]. Эта модель с допустимой инженерной точностью моделирует композитные материалы в случае неидеального контакта арматуры со связующим.

Простейшая структурная модель, учитывающая объемное соотношение компонентов, для расчета прочности волокнистого композита была предложена еще в 1965 г. [12]. Отмечено [13, 14], что во многих случаях слоисто-волокнистый композит на макроуровне можно рассматривать как пластическое тело, подчиняющееся положениям теории пластичности, и в предположении, что напряженное состояние в волокнах одномерное, определены предельные кривые для слоистых композитов с симметричным перекрестным армированием. На основе нитяной структурной модели, в которой не учитываются напряжения в связующем материале, и на основе метода предельного равновесия определены предельные нагрузки разнообразных полигональных железобетонных плит [15]. Рассматривалось численное моделирование упругопластического динамического поведения осесимметричных однослойных и многослойных пластин и оболочек переменной толщины из традиционных и композиционных материалов и отмечено [16], что при решении многих задач динамики композитных оболочек даже достаточно грубые модели пластического деформирования материала, как, например, жесткопластическая модель, позволяют во многих случаях получить адекватное представление о процессах деформирования. На основе модели идеального жесткопластического материала исследовано динамическое поведение разнообразных по форме криволинейных однородных пластин под действием распределенных динамических нагрузок [9, 17–21]. Аналогичные исследования выполнены для круглых и правильных полигональных армированных пластин [22–24].

Разные виды армирования в области пластических деформаций имеют свои особенности, поэтому они должны анализироваться отдельно. В связи с этим в настоящей работе рассматриваются гибридные композитные криволинейные пластины с жесткой вставкой, армированные волокнами в направлениях, параллельных (эквидистантных) и нормальных к контуру пластины, под действием кратковременных интенсивных динамических нагрузок взрывного типа. Разработана методика анализа динамического изгиба таких пластин, основанная на жесткопластическом анализе при использовании структурной модели армированного слоя с одномерным напряженным состоянием в волокнах [10, 11]. Считается, что механические характеристики материалов, составляющих слоистый пакет соразмерные (различающиеся не более чем на порядок). По толщине каждый слой имеет регулярную и квазиоднородную структуру, на границах между слоями выполняются условия идеального механического контакта. В этом случае для слоистых тонких пластин приемлемо использование традиционных гипотез Кирхгофа−Лява. В настоящей работе развивается модель деформирования, разработанная ранее [21], которая распространяется на слоисто-волокнистые гибридные армированные пластины с гладким невогнутым криволинейным контуром.

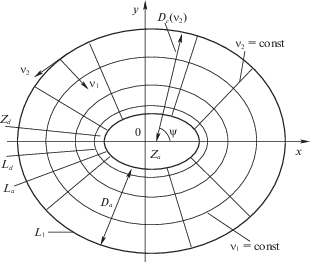
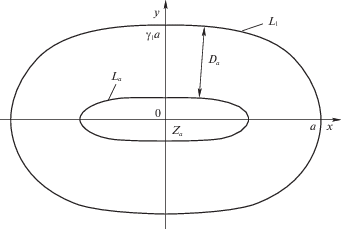
1. Формулировка задачи, основные геометрические соотношения и предположения. Рассмотрим тонкую кирхгофовскую пластину с гладким невогнутым криволинейным контуром, шарнирно опертым или защемленным (фиг. 1). Пластина находится под действием равномерно распределенной по поверхности взрывной нагрузки интенсивностью $P(t)$, которая характеризуется мгновенным достижением максимального значения ${{P}_{{\max }}} = P(0)$ в начальный момент времени $t = 0$ с последующим быстрым его уменьшением. Прогибы пластины считаются малыми. Влиянием мембранных сил и вертикальных сдвигов в условии пластичности и геометрическими изменениями пренебрегаем.

Фиг. 1

Пластина имеет произвольный гладкий невогнутый контур ${{L}_{1}}$, заданный в параметрическом виде

$x = {{x}_{1}}(\varphi ),\quad y = {{y}_{1}}(\varphi ),\quad 0 \leqslant \varphi < 2\pi $

Его радиус кривизны

$R(\varphi ) = \frac{{{{B}^{3}}(\varphi )}}{{(\partial {{x}_{1}}{\text{/}}\partial \varphi )({{\partial }^{2}}{{y}_{1}}{\text{/}}\partial {{\varphi }^{2}}) - ({{\partial }^{2}}{{x}_{1}}{\text{/}}\partial {{\varphi }^{2}})(\partial {{y}_{1}}{\text{/}}\partial \varphi )}}$

$B(\varphi ) = \sqrt {{{{(\partial {{x}_{1}}{\text{/}}\partial \varphi )}}^{2}} + {{{(\partial {{y}_{1}}{\text{/}}\partial \varphi )}}^{2}}} $

Для определенности будем рассматривать пластины, симметричные относительно оси $x$; геометрические размеры пластины по оси $y$ не больше, чем по оси $x$ (фиг. 1). Введем криволинейную ортогональную систему координат (${{\nu }_{1}},{{\nu }_{2}}$), связанную с декартовой системой координат ($x,y$) соотношениями (штрихом обозначена производная по координате ${{\nu }_{2}}$)

(1.1)

$x = {{x}_{1}}({{\nu }_{2}}) - {{\nu }_{1}}y_{1}^{'}({{\nu }_{2}}){\text{/}}B({{\nu }_{2}}),\quad y = {{y}_{1}}({{\nu }_{2}}) + {{\nu }_{1}}x_{1}^{'}({{\nu }_{2}}){\text{/}}B({{\nu }_{2}})$

Кривые ${{\nu }_{1}} = {\text{const}}$ находятся на расстоянии ${{\nu }_{1}}$ от контура ${{L}_{1}}$ внутрь пластины и имеют радиус кривизны ${{r}_{1}} = R({{\nu }_{2}}) - {{\nu }_{1}}$. Прямые ${{\nu }_{2}} = {\text{const}}$ перпендикулярны контуру ${{L}_{1}}$ (радиус кривизны ${{r}_{2}} = \infty $). В этом случае уравнение контура пластины ${{L}_{1}}$ имеет вид

${{\nu }_{1}} = 0,\quad 0 \leqslant {{\nu }_{2}} < 2\pi $

Выражение для элемента площади в координатах ${{\nu }_{1}},{{\nu }_{2}}$, угол между направлением ${{\nu }_{1}}$ и осью $x$ (фиг. 1) и дифференциал этого угла имеют вид

$ds = B({{\nu }_{2}})\left( {1 - \frac{{{{\nu }_{1}}}}{R}} \right)d{{\nu }_{1}}d{{\nu }_{2}},\quad \psi = - {\text{arctg}}\frac{{x_{1}^{'}({{\nu }_{2}})}}{{y_{1}^{'}({{\nu }_{2}})}},\quad d\psi = \frac{{B({{\nu }_{2}})}}{{R({{\nu }_{2}})}}d{{\nu }_{2}},$

поэтому для гладкого криволинейного контура ${{L}_{1}}$, симметричного относительно оси $x$, справедливо равенство

(1.2)

$\int\limits_0^\pi {\frac{{B({{\nu }_{2}})}}{{R({{\nu }_{2}})}}} d{{\nu }_{2}} = \int\limits_0^\pi d \psi = \pi $

Расстояние от контура ${{L}_{1}}$ до оси $x$ по нормали к контуру ${{L}_{1}}$ равно (фиг. 1)

(1.3)

${{D}_{c}}({{\nu }_{2}}) = \left| {\frac{{{{y}_{1}}({{\nu }_{2}})}}{{x_{1}^{'}({{\nu }_{2}})}}} \right|B({{\nu }_{2}})$

В центральной части пластины находится абсолютно жесткая вставка ${{Z}_{a}}$ с криволинейным контуром ${{L}_{a}}$. Считаем контуры ${{L}_{1}}$ и ${{L}_{a}}$ эквидистантными (расстояние между ними не зависит от координаты ${{\nu }_{2}}$). Тогда уравнение контура ${{L}_{a}}$ имеет вид

${{\nu }_{1}} = {{D}_{a}}{\text{ = const,}}\quad 0 \leqslant {{\nu }_{2}} < 2\pi $

Также считаем, что

$0 < {{D}_{a}} \leqslant \mathop {\min }\limits_{0 \leqslant {{\nu }_{2}} \leqslant \pi } {{D}_{c}}({{\nu }_{2}})$

поэтому перпендикуляры, опущенные из точек контура ${{L}_{1}}$ на контур ${{L}_{a}}$, не пересекаются. Например, для контура ${{L}_{1}}$ в форме эллипса с полуосями $a$ и $b$ справедливо неравенство $0 < {{D}_{a}} \leqslant {{b}^{2}}{\text{/}}a$.

Площадь жесткой вставки равна

(1.4)

${{S}_{a}} = \iint\limits_{{{Z}_{a}}} ds = 2\int\limits_0^\pi {\int\limits_{{{D}_{a}}}^{{{D}_{c}}({{\nu }_{2}})} {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})d{{\nu }_{1}}} } d{{\nu }_{2}};\quad {{\tilde {\nu }}_{1}} = \frac{{{{\nu }_{1}}}}{{R({{\nu }_{2}})}}$

Материал вставки однородный c поверхностной плотностью ${{\rho }_{a}}$. Остальная часть пластины выполнена из гибридного слоистого композитного материала с симметричным относительно ее срединной поверхности распределением слоев. Предполагается, что каждый слой содержит по толщине большое количество армированных элементарных слоев и связующих их изотропных прослоек, описываемых моделью идеального жесткопластического материала. В каждом слое возможно расположение волокон арматуры, выполненных из различных материалов, в параллельном (по линиям ${{\nu }_{1}} = {\text{const}}$) и нормальном (по линиям ${{\nu }_{2}} = {\text{const}}$) направлении к контуру пластины ${{L}_{1}}$. В разных слоях материалы арматуры и связующего различные. Структура армирования пластины из одних и тех же составляющих материалов может иметь разный вид за счет взаимного изменения порядка расположения армированных слоев.

Для рассматриваемой пластины приведенная поверхностная плотность материала в армируемой части пластины равна

$\rho ({{\nu }_{1}}) = 2\sum\limits_{k = 1}^n {{{\rho }_{k}}} ({{h}_{k}} - {{h}_{{k - 1}}}),\quad {{\rho }_{k}} = (1 - {{\omega }_{{1k}}} - {{\omega }_{{2k}}}){{\rho }_{{0k}}} + {{\omega }_{{1k}}}{{\rho }_{{1k}}} + {{\omega }_{{2k}}}{{\rho }_{{2k}}},$

где $n$ – половина общего количества слоев, ${{\rho }_{{0k}}}$ – плотность связующего материала в $k$-м слое, ${{\rho }_{{1k}}}$ – плотность материала арматуры в $k$-м слое в направлении, нормальном к контуру пластины ${{L}_{1}}$ (вдоль линий ${{\nu }_{2}} = {\text{const}}$; см. фиг. 1), ${{\rho }_{{2k}}}$ – плотность материала арматуры в $k$-м слое в направлении, параллельном контуру пластины (вдоль линий ${{\nu }_{1}} = {\text{const}}$), ${{\omega }_{{jk}}}({{\nu }_{1}})$ – плотность армирования (относительное объемное содержание волокон в слое) в $k$-м слое вдоль линий ${{\nu }_{{3 - j}}} = {\text{const}}$ ($j = 1,2$), в общем случае, зависящая от ${{\nu }_{1}}$, ${{h}_{k}}$ – координаты раздела слоев; ${{h}_{0}} = 0$, ${{h}_{n}} = H$, $2H$ – толщина пластины.

Для рассматриваемого вида армирования выражения предельных изгибающих моментов ${{M}_{{01}}}$ и ${{M}_{{02}}}$ (погонных), нормальных и тангенциальных к контуру пластины ${{L}_{1}}$, согласно структурной модели армированного слоя с одномерным напряженным состоянием в волокнах [10, 11], имеют вид

${{M}_{{0j}}}({{\nu }_{1}}) = \sum\limits_{k = 1}^n {{{\sigma }_{{0jk}}}} ({{\nu }_{1}})(h_{k}^{2} - h_{{k - 1}}^{2}),\quad j = 1,2$

${{\sigma }_{{0jk}}}({{\nu }_{1}}) = [1 - {{\omega }_{{jk}}}({{\nu }_{1}})]{{\sigma }_{{0k}}} + {{\omega }_{{jk}}}({{\nu }_{1}}){{\sigma }_{{jk}}}$

Здесь ${{\sigma }_{{0k}}}$ – предел текучести связующего материала в $k$-м слое, ${{\sigma }_{{jk}}}$ – предел текучести материала арматуры, расположенной вдоль направлений ${{\nu }_{j}}$ в $k$-м слое.

В зависимости от значения ${{P}_{{\max }}}$ возможны две схемы динамического деформирования рассматриваемой пластины. При нагрузках, не превышающих предельные нагрузки (при “низких” нагрузках), пластина остается в состоянии покоя. При нагрузках, незначительно превышающих предельные (при “средних” нагрузках), как и в случае круглых армированных пластин [22] и однородных криволинейных пластин [21], жесткая область ${{Z}_{a}}$ движется поступательно со скоростью ${{\dot {w}}_{a}}(t)$. В отличие от однородных пластин с жесткой вставкой при деформировании композитных пластин также может двигаться поступательно некоторая двусвязная жесткая область ${{Z}_{d}}$, расположенная около вставки (фиг. 1). Из непрерывности скоростей на контуре ${{L}_{a}}$ следует, что области ${{Z}_{d}}$ и ${{Z}_{a}}$ движутся с одинаковой скоростью ${{\dot {w}}_{a}}(t)$. Из непрерывности скоростей на внешнем контуре ${{L}_{d}}$ области ${{Z}_{d}}$ следует, что нормаль к линии ${{L}_{d}}$ является также нормалью к контуру ${{L}_{1}}$ и расстояние $d$ между ${{L}_{a}}$ и ${{L}_{d}}$ не зависит от координаты ${{\nu }_{2}}$. Уравнение контура ${{L}_{d}}$ имеет вид

${{\nu }_{1}} = \Delta ;\quad \Delta = {{D}_{a}} - d,\quad 0 \leqslant d < {{D}_{a}},\quad 0 \leqslant {{\nu }_{2}} < 2\pi $

Контур ${{L}_{d}}$ – пластический шарнир; на нем нормальный изгибающий момент равен предельному значению ${{M}_{{01}}}(\Delta )$. При $d = 0$ контур ${{L}_{d}}$ совпадает с контуром вставки ${{L}_{a}}$. Остальная часть пластины $Z$ деформируется в линейчатую поверхность. Такую схему движения назовем схемой 1. Величина $d$ определяется из условия минимума предельной нагрузки пластины, как это будет показано ниже.

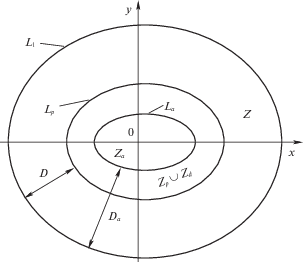
Как и в случаях изгиба армированных полигональных пластин [23], однородных криволинейных пластин [21], армированных круглых и кольцевых пластин [25, 26], при достаточно больших значениях ${{P}_{{\max }}}$ (при “высоких” нагрузках) динамическое деформирование армированной пластины может сопровождаться возникновением около области ${{Z}_{d}}$ двусвязной, движущейся поступательно, области ${{Z}_{p}}$, расположенной между контурами ${{L}_{d}}$ и ${{L}_{p}}$ (фиг. 2). Из непрерывности скоростей на контуре ${{L}_{d}}$ следует, что область ${{Z}_{p}}$ движется со скоростью ${{\dot {w}}_{a}}(t)$, как и область ${{Z}_{a}}$, нормаль к линии ${{L}_{p}}$ является также нормалью к контуру ${{L}_{1}}$ и расстояние $D$ между контурами ${{L}_{1}}$ и ${{L}_{p}}$ не зависит от координаты ${{\nu }_{2}}$, но зависит от времени. Уравнение контура ${{L}_{p}}$ имеет вид

${{\nu }_{1}} = D(t),\quad 0 < D(t) \leqslant \Delta ,\quad 0 \leqslant {{\nu }_{2}} < 2\pi $

Фиг. 2

Такую схему движения назовем схемой 2. Область $Z$ – часть пластины без областей ${{Z}_{p}}$, ${{Z}_{d}}$ и ${{Z}_{a}}$, она деформируется в линейчатую поверхность. В отличие от схемы 1 в схеме 2 положение контура ${{L}_{p}}$ изменяется со временем, а области ${{Z}_{a}} \cup {{Z}_{d}} \cup {{Z}_{p}}$ и $Z$ движутся независимо. Поэтому в схеме 1 пластина имеет одну степень свободы, а в схеме 2 – две.

2. Вывод уравнений движения и анализ поведения пластины. Схема 1. Уравнение движения пластины выведем из принципа виртуальной мощности с использованием принципа Даламбера [27]

(2.1)

$K = A - N$

(2.2)

$K = \iint\limits_{{{Z}_{a}}} {{{\rho }_{a}}\ddot {u}}\dot {u}{\text{*}}ds + \iint\limits_{{{Z}_{d}} \cup {{Z}_{p}} \cup Z} {\rho \ddot {u}}\dot {u}{\text{*}}ds,\quad A = \iint\limits_S {P(t)}\dot {u}{\text{*}}ds$

Здесь $K$, $A$ и $N$ – мощности инерционных, внешних и внутренних сил соответственно, $S$ – площадь пластины, $u$ – прогиб. Точками над символами обозначены производные по времени. Звездочкой обозначены кинематически допустимые величины. Выражение для $N$ запишем ниже.

Обозначим через $\dot {\alpha }$ угловую скорость поворота пластины (по нормали к контуру ${{L}_{1}}$) на опорном контуре ${{L}_{1}}$. Из условия непрерывности скоростей на контурах ${{L}_{p}}$ и ${{L}_{d}}$ следует, что $\dot {\alpha }$ не зависит от параметра ${{\nu }_{2}}$, а для схемы 1

$\dot {\alpha } = {{\dot {w}}_{a}}(t){\text{/}}\Delta $

Рассмотрим схему 1. Скорости прогибов пластины

(2.3)

$\begin{gathered} ({{\nu }_{1}},{{\nu }_{2}}) \in {{Z}_{a}} \cup {{Z}_{d}}{\text{:}}\quad \dot {u}({{\nu }_{1}},{{\nu }_{2}},t) = {{{\dot {w}}}_{a}}(t) \\ ({{\nu }_{1}},{{\nu }_{2}}) \in Z{\text{:}}\quad \dot {u}({{\nu }_{1}},{{\nu }_{2}},t) = {{\nu }_{1}}{{{\dot {w}}}_{a}}(t){\text{/}}\Delta \\ \end{gathered} $

Главные кривизны поверхности скоростей прогибов в области $Z$

(2.4)

${{\kappa }_{1}} = - \frac{{{{\partial }^{2}}\dot {u}}}{{\partial \nu _{1}^{2}}} = 0,\quad {{\kappa }_{2}} = - \frac{1}{{{{r}_{1}}}}\frac{{\partial{ \dot {u}}}}{{\partial {{\nu }_{1}}}} = - \frac{{{{{\dot {w}}}_{a}}(t)}}{{\Delta [R({{\nu }_{2}}) - {{\nu }_{1}}]}}$

Выражения (2.2) для мощностей $K$ и $A$ при ${{Z}_{p}} = \emptyset $ и учете соотношений (1.2), (1.4) и (2.3) принимают вид

(2.5)

$\begin{gathered} K = {{{\ddot {w}}}_{a}}(t)\dot {w}_{a}^{ * }(t)\left[ {{{\rho }_{a}}{{S}_{a}} + 2\int\limits_0^\pi {\int\limits_\Delta ^{{{D}_{a}}} {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})d{{\nu }_{1}}d{{\nu }_{2}} + } } } \right. \\ + \;\frac{2}{{{{\Delta }^{2}}}}\left. {\int\limits_0^\pi {\int\limits_0^\Delta {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})\nu _{1}^{2}d{{\nu }_{1}}d{{\nu }_{2}}} } } \right] \\ \end{gathered} $

(2.6)

$A = P\dot {w}_{a}^{ * }{{S}_{a}} + \left[ {2\int\limits_0^\pi {\int\limits_\Delta ^{{{D}_{a}}} {B(1 - {{{\tilde {\nu }}}_{1}})d{{\nu }_{1}}d{{\nu }_{2}} + \frac{2}{\Delta }\int\limits_0^\pi {\int\limits_0^\Delta {B(1 - {{{\tilde {\nu }}}_{1}}){{\nu }_{1}}d{{\nu }_{1}}} } d{{\nu }_{2}}} } } \right]$

Мощность внутренних сил при схеме 1 равна сумме мощностей внутренних сил ${{N}_{1}}$, ${{N}_{2}}$ и ${{N}_{3}}$ на контурах ${{L}_{1}}$, ${{L}_{d}}$ и в области $Z$, соответственно:

$N = {{N}_{1}} + {{N}_{2}} + {{N}_{3}}$

${{N}_{1}} = (1 - \eta ){{M}_{{01}}}(0)\,\oint\limits_{{{L}_{1}}} {{{{[\dot {\theta }{\text{*}}]}}_{{{{L}_{1}}}}}} dl,\quad dl = Bd{{\nu }_{2}}$

${{N}_{2}} = {{M}_{{01}}}(\Delta )\,\oint\limits_{{{L}_{d}}} {{{{[\dot {\theta }{\text{*}}]}}_{{{{L}_{d}}}}}} d{{l}_{d}},\quad d{{l}_{d}} = B(1 - \Delta {\text{/}}R)d{{\nu }_{2}}$

${{N}_{3}} = \iint\limits_Z {{{M}_{{02}}}}({{\nu }_{1}}{\text{)|}}\kappa _{2}^{ * }{\kern 1pt} {\text{|}}ds$

Здесь ${{[\dot {\theta }]}_{L}}$ – разрыв угловой скорости на линии $L$, $dl$ и $d{{l}_{d}}$ – элементы длины линий ${{L}_{1}}$ и ${{L}_{d}}$, $\eta = 0$ при защемлении контура ${{L}_{1}}$ и $\eta = 1$ при его шарнирном опирании. Из соотношений (2.3), поскольку нормаль к линии ${{L}_{d}}$ является нормалью к контуру ${{L}_{1}}$, следует

${{[\dot {\theta }]}_{{{{L}_{1}}}}} = {{[\dot {\theta }]}_{{{{L}_{d}}}}} = \frac{{{{{\dot {w}}}_{a}}(t)}}{\Delta }$

Тогда, учитывая соотношения (1.2) и (2.4) и введя обозначение

(2.7)

$I = \int\limits_0^\pi B d{{\nu }_{2}}$

получим

${{N}_{1}} = 2(1 - \eta ){{M}_{{01}}}(0)\frac{{{{{\dot {w}}}_{a}}(t)}}{\Delta }I$

${{N}_{2}} = {{M}_{{01}}}(\Delta )\frac{{\dot {w}_{a}^{ * }(t)}}{\Delta }\int\limits_0^{2\pi } B \left( {1 - \frac{\Delta }{R}} \right)d{{\nu }_{2}} = 2{{M}_{{01}}}(\Delta )\frac{{\dot {w}_{a}^{ * }(t)}}{\Delta }(I - 2\pi \Delta )$

${{N}_{3}} = \frac{{{{{\dot {w}}}_{a}}(t)}}{\Delta }\int\limits_0^{2\pi } {\int\limits_0^\Delta {{{M}_{{02}}}({{\nu }_{1}})} } \frac{{B({{\nu }_{2}})}}{{R - {{\nu }_{1}}}}(1 - {{\tilde {\nu }}_{1}})d{{\nu }_{1}}d{{\nu }_{2}} = $

$ = \frac{{{{{\dot {w}}}_{a}}(t)}}{\Delta }\int\limits_0^{2\pi } {\frac{{B({{\nu }_{2}})}}{{R({{\nu }_{2}})}}} d{{\nu }_{2}}\int\limits_0^\Delta {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}} = 2\pi \frac{{{{{\dot {w}}}_{a}}(t)}}{\Delta }\int\limits_0^\Delta {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}}$

Полная мощность внутренних сил пластины для схемы 1

$N = \frac{{2\dot {w}_{a}^{ * }(t)}}{\Delta }\left[ {(1 - \eta ){{M}_{{01}}}(0)I + {{M}_{{01}}}(\Delta )(I - \pi \Delta ) + \pi \int\limits_0^\Delta {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}}} \right]$

Подставляя последнее выражение, а также выражения (2.5) и (2.6) в равенство (2.1) и учитывая соотношение (1.2) и то, что $\dot {w}_{a}^{{\text{*}}}(t)$ – независимая функция, получим уравнение движения

${{\ddot {w}}_{a}}(t){{\Omega }_{1}}(d) = P(t){{\Omega }_{2}}(d) - {{\Omega }_{3}}(d)$

(2.8)

$\begin{gathered} {{\Omega }_{1}}(d) = \Delta \left[ {{{\rho }_{a}}{{S}_{a}} + 2\int\limits_0^\pi {\int\limits_\Delta ^{{{D}_{a}}} {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})d{{\nu }_{1}}d{{\nu }_{2}}} } } \right] + \frac{2}{\Delta }\int\limits_0^\pi {\int\limits_0^\Delta {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})\nu _{1}^{2}d{{\nu }_{1}}d{{\nu }_{2}}} } \\ {{\Omega }_{2}}(d) = \frac{\Delta }{3}\{ 3{{S}_{a}} + 3d[2I - \pi ({{D}_{a}} + \Delta )] + \Delta (3I - 2\pi \Delta )\} \\ \end{gathered} $

${{\Omega }_{3}}(d) = 2\left[ {(1 - \eta ){{M}_{{01}}}(0)I + {{M}_{{01}}}\Delta (I - \pi \Delta ) + \pi \int\limits_0^\Delta {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}}} \right]$

Предельную нагрузку определим из уравнения (2.8) в момент начала деформации $t = 0$, принимая ${{\ddot {w}}_{a}}(0) = 0$:

(2.9)

${{P}_{0}} = \mathop {\min }\limits_{0 \leqslant d < {{D}_{a}}} \frac{{{{\Omega }_{3}}(d)}}{{{{\Omega }_{2}}(d)}} = \frac{{{{\Omega }_{3}}({{d}_{0}})}}{{{{\Omega }_{2}}({{d}_{0}})}}$

Расстояние ${{d}_{0}}$ определяет положение контура ${{L}_{d}}$ в предельном состоянии. Отметим, что когда плотности армирования ${{\omega }_{{2k}}}$ ($k = 1,\; \ldots ,\;n$) не зависят от координаты ${{\nu }_{1}}$, из анализа выражения (2.9) следует, что для оценки предельной нагрузки достаточно знать только одну интегральную характеристику (2.7) – половину длины внешнего контура пластины.

Поведение пластины при схеме 1 описывается уравнением (2.8) при $d = {{d}_{0}}$

(2.10)

${{\ddot {w}}_{a}}(t){{\Omega }_{1}}({{d}_{0}}) = P(t){{\Omega }_{2}}({{d}_{0}}) - {{\Omega }_{3}}({{d}_{0}})$

с начальными условиями

(2.11)

${{\dot {w}}_{a}}(0) = {{w}_{a}}(0) = 0$

Схема 1 реализуется для значений ${{P}_{0}} < {{P}_{{\max }}} \leqslant {{P}_{1}}$ (“средние” нагрузки), где ${{P}_{1}}$ – минимальное значение амплитуды нагрузки ${{P}_{{\max }}}$, при котором движение начнется со схемы 2. Величину ${{P}_{1}}$ определим ниже при анализе схемы 2.

Запишем уравнение движения (2.10) в виде

(2.12)

${{\ddot {w}}_{a}}(t) = G[P(t) - {{P}_{0}}],\quad G = {{\Omega }_{2}}({{d}_{0}}){\text{/}}{{\Omega }_{1}}({{d}_{0}})$

Пусть в момент времени $t = T$ нагрузка снимается. При $0 \leqslant t \leqslant T$, интегрируя уравнение (2.12), имеем

${{\dot {w}}_{a}}(t) = G\left[ {\int\limits_0^t {P(\tau )d\tau - } {{P}_{0}}t]} \right],\quad {{w}_{a}}(t) = G\left[ {\int\limits_0^t {\int\limits_0^q {P(\tau )d\tau dq} } - {{P}_{0}}\frac{{{{t}^{2}}}}{2}} \right]$

Если нагрузка $P(t)$ такова, что в некоторый момент времени ${{t}_{s}} \leqslant T$ выполняется равенство ${{\dot {w}}_{a}}({{t}_{s}}) = 0$, то тогда

${{t}_{s}} = \frac{1}{{{{P}_{0}}}}\int\limits_0^{{{t}_{s}}} {P(t)dt} $

и в этот момент ${{t}_{s}}$ пластина остановится еще во время действия нагрузки, при этом максимальный остаточный прогиб будет равен ${{w}_{a}}({{t}_{s}})$.

Если ${{\dot {w}}_{a}}(t) > 0$ при любом $t \in [0,T]$, то при $T < t \leqslant {{t}_{f}}$ движение пластины после снятия нагрузки продолжается по инерции до остановки в момент ${{t}_{f}}$ и описывается уравнением

(2.13)

${{\ddot {w}}_{a}}(t) = - G{{P}_{0}}$

с начальными данными ${{\dot {w}}_{a}}(T)$, ${{w}_{a}}(T)$. Момент ${{t}_{f}}$ определяется из условия

(2.14)

${{\dot {w}}_{a}}({{t}_{f}}) = 0$

Интегрируя уравнение движения (2.13), получим

(2.15)

${{\dot {w}}_{a}}(t) = {{\dot {w}}_{a}}(T) - G{{P}_{0}}(t - T)$

(2.16)

${{w}_{a}}(t) = {{w}_{a}}(T) + {{w}_{a}}(T)(t - T) - G{{P}_{0}}{{(t - T)}^{2}}{\text{/}}2$

Из уравнений (2.14) и (2.15) следует

(2.17)

${{t}_{f}} = \frac{1}{{{{P}_{0}}}}\int\limits_0^T {P(t)dt} $

Максимальный остаточный прогиб равен

${{w}_{a}}({{t}_{f}}) = G\left[ {\frac{1}{{2{{P}_{0}}}}{{{\left( {\int\limits_0^T {P(t)dt} } \right)}}^{2}} - \int\limits_0^T {tP(t)d} t} \right]$

Все прогибы в пластине определяются соотношениями (2.3).

3. Вывод уравнений движения и анализ поведения пластины. Схема 2. Рассмотрим схему 2 (фиг. 2). Скорости прогибов пластины определяются выражениями

(3.1)

$\begin{gathered} ({{\nu }_{1}},{{\nu }_{2}}) \in {{Z}_{p}} \cup {{Z}_{d}} \cup {{Z}_{a}}{\text{:}}\quad \dot {u}({{\nu }_{1}},{{\nu }_{2}},t) = {{{\dot {w}}}_{a}}(t) \\ ({{\nu }_{1}},{{\nu }_{2}}) \in Z{\text{:}}\quad \dot {u}({{\nu }_{1}},{{\nu }_{2}},t) = \dot {\alpha }(t){{\nu }_{1}}, \\ \end{gathered} $

а главные кривизны поверхности скоростей прогибов в области $Z$

(3.2)

${{\kappa }_{1}} = - \frac{{{{\partial }^{2}}\dot {u}}}{{\partial \nu _{1}^{2}}} = 0,\quad {{\kappa }_{2}} = - \frac{1}{{{{r}_{1}}}}\frac{{\partial{ \dot {u}}}}{{\partial {{\nu }_{1}}}} = - \frac{{\dot {\alpha }(t)}}{{R({{\nu }_{2}}) - {{\nu }_{1}}}}$

Выражения (2.2) для схемы деформирования 2 примут вид

(3.3)

$\begin{gathered} K = {{{\ddot {w}}}_{a}}(t)\dot {w}_{a}^{ * }(t)\left[ {{{\rho }_{a}}{{S}_{a}} + 2\int\limits_0^\pi {\int\limits_D^{{{D}_{a}}} {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})d{{\nu }_{1}}d{{\nu }_{2}}} } } \right] + \\ + \;2\ddot {\alpha }(t)\dot {\alpha }{\text{*}}(t)\int\limits_0^\pi {\int\limits_0^D {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})\nu _{1}^{2}d{{\nu }_{1}}d{{\nu }_{2}}} } \\ \end{gathered} $

(3.4)

$A = P(t)\left\{ {\dot {w}_{a}^{ * }(t)\left[ {{{S}_{a}} + 2\int\limits_0^\pi {\int\limits_D^{{{D}_{a}}} {B(1 - {{{\tilde {\nu }}}_{1}})d{{\nu }_{1}}d{{\nu }_{2}}} } } \right] + 2\dot {\alpha }{\text{*}}(t)\int\limits_0^\pi {\int\limits_0^D {B(1 - {{{\tilde {\nu }}}_{1}}){{\nu }_{1}}d{{\nu }_{1}}d{{\nu }_{2}}} } } \right\}$

Мощность внутренних сил при схеме 2 равна сумме мощностей внутренних сил ${{N}_{1}}$, ${{N}_{2}}$ и ${{N}_{3}}$ на контурах ${{L}_{1}}$, ${{L}_{p}}$ и в области $Z$, соответственно (фиг. 2):

$N = {{N}_{1}} + {{N}_{2}} + {{N}_{3}}$

${{N}_{1}} = (1 - \eta ){{M}_{{01}}}(0)\,\oint\limits_{{{L}_{1}}} {{{{[\dot {\theta }{\text{*}}]}}_{{{{L}_{1}}}}}} dl$

${{N}_{2}} = {{M}_{{01}}}(D)\,\oint\limits_{{{L}_{p}}} {{{{[\dot {\theta }{\text{*}}]}}_{{{{L}_{p}}}}}} d{{l}_{p}},\quad d{{l}_{p}} = B(1 - D{\text{/}}R)d{{\nu }_{2}},\quad {{N}_{3}} = \iint\limits_Z {{{M}_{{02}}}}({{\nu }_{1}}{\text{)|}}\kappa _{2}^{ * }{\kern 1pt} {\text{|}}ds$

Из соотношений (3.1) при учете того, что линия ${{L}_{p}}$ и контур ${{L}_{1}}$ имеют общую нормаль, следует, что разрыв угловой скорости на ${{L}_{1}}$ и на ${{L}_{p}}$ равен $\dot {\alpha }(t)$, т.е. ${{[\dot {\theta }]}_{{{{L}_{1}}}}}$ = ${{[\dot {\theta }]}_{{{{L}_{p}}}}}$ = $\dot {\alpha }(t)$. Тогда, учитывая соотношения (1.2) и (3.2), аналогично случаю схемы 1 получаем выражения для полной мощности внутренних сил пластины при схеме 2

(3.5)

$N = 2\dot {\alpha }{\text{*}}\left[ {(1 - \eta ){{M}_{{01}}}(0)I + {{M}_{{01}}}(D)(I - \pi D) + \pi \int\limits_0^D {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}}} \right]$

Подставляя выражения (3.3)–(3.5) в равенство (2.1) и учитывая, что $\dot {\alpha }{\text{*}}$ и $\dot {w}_{a}^{ * }$ независимы, получим уравнения движения пластины в случае деформирования по схеме 2

(3.6)

${{\ddot {w}}_{a}}(t) = P(t){{\Sigma }_{1}}(D(t))$

(3.7)

$\ddot {\alpha }(t) = P(t){{\Sigma }_{2}}(D(t)) - {{\Sigma }_{3}}(D(t)),$

где

${{\Sigma }_{1}}(D) = \left[ {{{S}_{a}} + 2\int\limits_0^\pi {\int\limits_D^{{{D}_{a}}} {B(1 - {{{\tilde {\nu }}}_{1}})d{{\nu }_{1}}d{{\nu }_{2}}} } } \right]{{\left[ {{{\rho }_{a}}{{S}_{a}} + 2\int\limits_0^\pi {\int\limits_D^{{{D}_{a}}} {B(1 - {{{\tilde {\nu }}}_{1}})\rho d{{\nu }_{1}}d{{\nu }_{2}}} } } \right]}^{{ - 1}}}$

${{\Sigma }_{2}}(D) = \int\limits_0^\pi {\int\limits_0^D {B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}}){{\nu }_{1}}d{{\nu }_{1}}d{{\nu }_{2}}} } {{\left[ {\int\limits_0^\pi {\int\limits_0^D {B(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})\nu _{1}^{2}d{{\nu }_{1}}d{{\nu }_{2}}} } } \right]}^{{ - 1}}}$

${{\Sigma }_{3}}(D) = \left[ {(1 - \eta ){{M}_{{01}}}(0)I + {{M}_{{01}}}(D)(I - \pi D) + \pi \int\limits_0^D {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}}} \right] \times $

$ \times \;{{\left[ {\int\limits_0^\pi {\int\limits_0^D {B(1 - {{{\tilde {\nu }}}_{1}})\rho ({{\nu }_{1}})\nu _{1}^{2}d{{\nu }_{1}}d{{\nu }_{2}}} } } \right]}^{{ - 1}}}$

Из непрерывности скоростей на границах областей $Z$ и ${{Z}_{p}}$ следует

(3.8)

$\dot {\alpha }D = {{\dot {w}}_{a}}$

Начальные условия имеют вид (2.11) и

(3.9)

$\dot {\alpha }(0) = \alpha (0) = 0$

Начальные значения ${{D}_{0}} = D(0)$, определяются в зависимости от значения ${{P}_{{\max }}}$, как будет показано ниже.

Система уравнений (3.6)–(3.8) для функций $\dot {\alpha }$, ${{\dot {w}}_{a}}$ и $D$ с начальными условиями (2.11), (3.9) и ${{D}_{0}} = D(0)$ описывает поведение армированной пластины в случае деформирования по схеме 2.

Продифференцировав уравнение (3.8) по времени, подставим полученное выражение для ${{\ddot {w}}_{a}}$ в уравнение (3.6) и исключим из него величину $\ddot {\alpha }$ с помощью уравнения (3.7). В результате получим уравнение

(3.10)

$\dot {\alpha }(t)\dot {D}(t) = P(t)\left[ {{{\Sigma }_{1}}(D(t)) - D(t){{\Sigma }_{2}}(D(t))} \right] + {{\Sigma }_{3}}(D(t))D(t),$

которое в начальный момент при учете условий (3.9) можно записать в виде

(3.11)

${{P}_{{\max }}} = {{\Sigma }_{3}}({{D}_{0}}){{D}_{0}}{{\left[ {{{\Sigma }_{2}}({{D}_{0}}){{D}_{0}} - {{\Sigma }_{1}}({{D}_{0}})} \right]}^{{ - 1}}}$

Считая, что при возникновении области ${{Z}_{p}}$ выполняются равенства

${{P}_{{\max }}} = {{P}_{1}},\quad {{D}_{0}} = {{D}_{a}} - {{d}_{0}},$

из выражения (3.11) получаем значение нагрузки

(3.12)

${{P}_{1}} = {{\Sigma }_{3}}({{D}_{a}} - {{d}_{0}}){{[{{\Sigma }_{2}}({{D}_{a}} - {{d}_{0}}) - {{\Sigma }_{1}}({{D}_{a}} - {{d}_{0}}){\text{/}}({{D}_{a}} - {{d}_{0}})]}^{{ - 1}}}$

Рассмотрим подробно поведение пластины под действием “высокой” нагрузки при ${{P}_{{\max }}} \geqslant {{P}_{1}}$. В этом случае движение пластины начнется с развитой областью ${{Z}_{p}}$ и ${{D}_{0}} < {{D}_{a}} - {{d}_{0}}$. В первой фазе ($0 < t \leqslant {{t}_{1}}$) деформирования движение происходит по схеме 2 и описывается уравнениями (3.6)–(3.8) с начальными условиями (2.11), (3.9) и ${{D}_{0}} = D(0)$. Величина ${{D}_{0}}$ определяется в зависимости от нагрузки ${{P}_{{\max }}}$ из соотношения (3.11). В этой фазе область ${{Z}_{p}}$ изменяется по закону (3.10), причем, если $P(t) = {\text{const}}$, то $\dot {D} = 0$ и $D(t) \equiv {{D}_{0}}$, а если функция $P(t)$ убывает или равна нулю, то $\dot {D} > 0$ и функция $D(t)$ возрастает. Когда величина $D$ достигает значения ${{D}_{a}}$, области ${{Z}_{p}}$ и ${{Z}_{d}}$ исчезают, пластина начинает деформироваться по схеме 1 при ${{d}_{0}} = 0$ и время ${{t}_{1}}$ определяется из равенства $D({{t}_{1}}) = {{D}_{a}}$. В этот момент определяются значения ${{\dot {w}}_{a}}({{t}_{1}})$, ${{w}_{a}}({{t}_{1}})$, $\dot {\alpha }({{t}_{1}})$ и $\alpha ({{t}_{1}})$. Во второй фазе (${{t}_{1}} < t \leqslant {{t}_{f}}$) движение пластины происходит по схеме 1 при ${{d}_{0}} = 0$ до остановки в момент времени ${{t}_{f}}$. Начальные условия для изучаемых функций равны соответствующим значениям в конце первой фазы. Время остановки определяется условием (2.14). Все прогибы пластины вычисляются из соотношений (3.1) и (2.3) с учетом обеих фаз движения. Определяющая система уравнений при схеме деформирования 2 в приведенных ниже примерах решалась численно методом Рунге–Кутты.

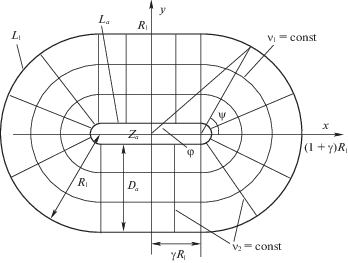
4. Численные примеры. Пластина с контуром, состоящим из двух полуокружностей и двух отрезков прямой. Рассмотрим армированную пластину с гладким контуром, состоящим из двух полуокружностей радиуса ${{R}_{1}}$ и двух отрезков прямой длиной $2\gamma {{R}_{1}}$ ($\gamma \geqslant 0$, см. фиг. 3). В силу симметрии запишем параметрические уравнения контура для четверти пластины

${{L}_{1}}:x(\varphi ) = \left\{ \begin{gathered} {{R}_{1}}(\gamma + \cos \psi ),\quad y(\varphi ) = {{R}_{1}}\sin \psi ,\quad 0 \leqslant \varphi \leqslant {{\varphi }_{0}} \hfill \\ {{R}_{1}}\operatorname{ctg} \varphi ,\quad y(\varphi ) = {{R}_{1}}{\text{,}}\quad {{\varphi }_{0}} \leqslant \varphi \leqslant \pi {\text{/}}2 \hfill \\ \end{gathered} \right.$

$\psi = \varphi + a\arcsin (\gamma \sin \varphi ),\quad {{\varphi }_{0}} = \operatorname{arctg} (1{\text{/}}\gamma )$

Фиг. 3

Соотношения (1.1) для координат ($x,y$) и (${{\nu }_{1}},{{\nu }_{2}}$) примут вид

$x = {{R}_{1}}[\gamma + \cos \psi ] - {{\nu }_{1}}\cos \psi ,\quad y = {{R}_{1}}\sin \psi - {{\nu }_{1}}\sin \psi \quad {\text{п р и }}\quad 0 \leqslant {{\nu }_{2}} \leqslant {{\varphi }_{0}}$

$x = {{R}_{1}}\operatorname{ctg} {{\nu }_{2}},\quad y = {{R}_{1}} - {{\nu }_{1}}\quad {\text{п р и }}\quad {{\varphi }_{0}} \leqslant {{\nu }_{2}} \leqslant \pi {\text{/}}2$

$\psi = {{\nu }_{2}} + a\arcsin (\gamma \sin {{\nu }_{2}})$

Также имеем

${{D}_{c}}({{\nu }_{2}}) = {{R}_{1}}\quad {\text{п р и }}\quad 0 \leqslant {{\nu }_{2}} \leqslant \pi {\text{/}}2,\quad R({{\nu }_{2}}) = \left\{ {\begin{array}{*{20}{l}} {{{R}_{1}},\quad 0 \leqslant {{\nu }_{2}} \leqslant {{\varphi }_{0}}} \\ {\infty ,\quad {{\varphi }_{0}} \leqslant {{\nu }_{2}} \leqslant \pi {\text{/}}2} \end{array}} \right.$

$B({{\nu }_{2}}) = \left\{ \begin{gathered} {{R}_{1}}(1 + \gamma \cos {{\nu }_{2}}{\text{/}}\sqrt {1 - {{\gamma }^{2}}{{{\sin }}^{2}}{{\nu }_{2}}} ),\quad 0 \leqslant {{\nu }_{2}} \leqslant {{\varphi }_{0}} \hfill \\ {{R}_{1}}{\text{/}}{{\sin }^{2}}{{\nu }_{2}},\quad {{\varphi }_{0}} \leqslant {{\nu }_{2}} \leqslant \pi {\text{/}}2 \hfill \\ \end{gathered} \right.$

Уравнение внешнего контура

${{L}_{a}}:{{\nu }_{1}} = {{D}_{a}},\quad 0 < {{D}_{a}} < {{R}_{1}}$

Для площади вставки и полудлины внешнего контура пластины имеем

${{S}_{a}} = ({{R}_{1}} - {{D}_{a}})[4\gamma {{R}_{1}} + \pi ({{R}_{1}} - {{D}_{a}})],\quad I = {{I}_{1}} = {{R}_{1}}(2\gamma + \pi )$

Поэтому на основании выражения (2.9) получим, что предельная нагрузка для рассматриваемой пластины определяется равенством

(4.1)

$\begin{gathered} {{P}_{0}} = 6\mathop {\min }\limits_{0 \leqslant d < {{D}_{a}}} \left\{ {(1 - \eta ){{M}_{{01}}}(0){{I}_{1}} + {{M}_{{01}}}(\Delta )({{I}_{1}} - \pi \Delta ) + \pi \int\limits_0^\Delta {{{M}_{{02}}}({{\nu }_{1}})} d{{\nu }_{1}}} \right\} \times \\ \times \;{{\Delta }^{{ - 1}}}{{\{ 3({{R}_{1}} - {{D}_{a}})(4\gamma {{R}_{1}} + \pi \Delta ) + 3d[2{{I}_{1}} - \pi ({{D}_{a}} - \Delta )] + \Delta (3{{I}_{1}} - 2\pi \Delta )\} }^{{ - 1}}}, \\ \end{gathered} $

из анализа которого видно уменьшение ${{P}_{0}}$ с увеличением параметра $\gamma $ при одинаковых остальных параметрах пластины.

Рассмотрим четырехслойную пластину при следующих значениях параметров:

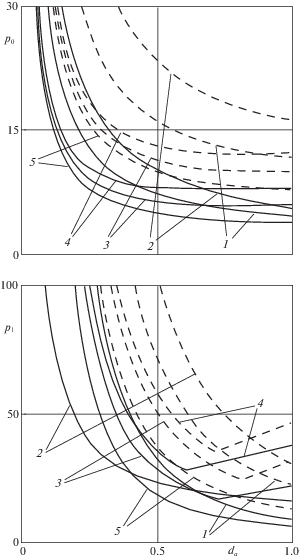
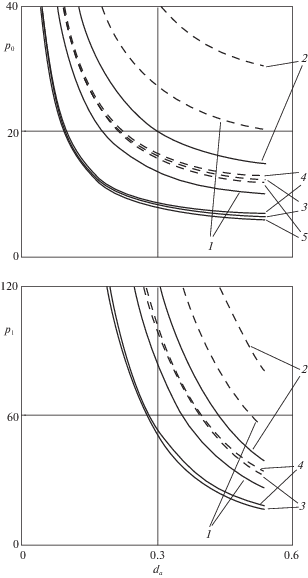
$n = 2,\quad {{h}_{1}} = 0.85H,\quad {{h}_{2}} = H,\quad {{\rho }_{{0k}}} = {{\rho }_{0}},\quad {{\rho }_{{jk}}}{\text{/}}{{\rho }_{0}} = {{\rho }_{a}}{\text{/}}{{\rho }_{0}} = 3$

${{\sigma }_{{jk}}} = {{\sigma }_{j}},\quad {{\sigma }_{{0k}}} = {{\sigma }_{0}},\quad {{\sigma }_{j}} = 10{{\sigma }_{0}},\quad j,k = 1,2$

Такое соотношение значений армирующих параметров возможно, например, если связующий материал – алюминий, а материал вставки и арматуры – сталь. Для рассматриваемой пластины при $\gamma = 0.5$ в верхней части фиг. 4 приведены зависимости безразмерной предельной нагрузки ${{p}_{0}} = {{P}_{0}}R_{1}^{2}{\text{/}}({{\sigma }_{0}}{{H}^{2}})$ от безразмерного размера вставки ${{d}_{a}} = {{D}_{a}}{\text{/}}{{R}_{1}}$, вычисленные по формуле (4.1), при разных значениях условий закрепления на контуре пластины и плотностей армирования ${{\omega }_{{jk}}}$ ($j,k = 1,2$) при условии одинакового расхода арматуры в случае, когда в каждом слое расположено только одно семейство арматуры

(4.2)

$\begin{gathered} {{h}_{1}}\int\limits_0^\pi {\int\limits_0^{{{D}_{a}}} {{{\omega }_{{i1}}}({{\nu }_{1}})B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})d{{\nu }_{1}}d{{\nu }_{2}}} } + \\ + \;({{h}_{2}} - {{h}_{1}})\int\limits_0^\pi {\int\limits_0^{{{D}_{a}}} {{{\omega }_{{m2}}}({{\nu }_{1}})B({{\nu }_{2}})(1 - {{{\tilde {\nu }}}_{1}})d{{\nu }_{1}}d{{\nu }_{2}}} } = {\text{const,}}\quad i,m = 1,2 \\ \end{gathered} $

Фиг. 4

Полагая, что функции ${{\omega }_{{jk}}}$ не зависят от координаты ${{\nu }_{1}}$, условие (4.2) в расчетах принимали в виде

(4.3)

${{h}_{1}}{{\omega }_{{i1}}} + ({{h}_{2}} - {{h}_{1}}){{\omega }_{{m2}}} = {\text{const}} = {\text{0}}{\text{.1}}$

Отметим, что для выполнения условия постоянства плотности армирования ${{\omega }_{{1k}}}$ в каждом слое толщина армирующих волокон должна быть переменной.

На фиг. 4 сплошные кривые относятся к шарнирному опиранию контура, штриховые – к его защемлению. Кривые 1–4 соответствуют значениям ${{\omega }_{{11}}}$ = 0.1/0.85 ≈ 0.118, ${{\omega }_{{12}}}$ = 0.1/0.15 ≈ 0.667, ${{\omega }_{{21}}}$ = 0.1/0.85, ${{\omega }_{{22}}}$ = 0.1/0.15; остальные значения плотности армирования равны нулю. Кривые 5 соответствуют значениям ${{p}_{0}}$ для неармированной пластины. Численно получено, что в случаях 1, 2 и 5 (для них справедливо неравенство ${{M}_{{01}}} \geqslant {{M}_{{02}}}$), величина ${{d}_{0}} \equiv 0$, независимо от размера вставки и способа крепления контура пластины, при этом в предельном состоянии пластический шарнир ${{L}_{d}}$ совпадает с контуром жесткой вставки ${{L}_{a}}$. В случаях армирования 3 и 4 (${{M}_{{01}}} < {{M}_{{02}}}$), когда арматура расположена вдоль линий ${{\nu }_{1}} = {\text{const}}$, величина ${{d}_{0}}$ может быть больше нуля.

Для рассматриваемой пластины функции ${{\Sigma }_{i}}(D)$ ($i = 1,2,3$) в системе уравнений движения (3.6), (3.7) имеют вид

${{\Sigma }_{1}}(D) = ({{\xi }_{1}} + {{\xi }_{2}}){\text{/}}({{\rho }_{a}}{{\xi }_{1}} + \rho {{\xi }_{2}})$

${{\Sigma }_{2}}(D) = 2\left[ {3{{R}_{1}}(2\gamma + \pi ) - 2\pi D} \right]{\text{/}}(\rho D{{\xi }_{3}})$

(4.4)

${{\Sigma }_{3}}(D) = 12\left[ {(2 - \eta ){{M}_{{01}}}{{R}_{1}}(2\gamma + \pi ) - \pi D({{M}_{{02}}} - {{M}_{{01}}})} \right]{\text{/}}(\rho {{D}^{3}}{{\xi }_{3}})$

${{\xi }_{1}} = ({{R}_{1}} - {{D}_{a}})[4\gamma {{R}_{1}} + \pi ({{R}_{1}} - {{D}_{a}})]$

${{\xi }_{2}} = ({{D}_{a}} - D)[2{{R}_{1}}(2\gamma + \pi ) - \pi ({{D}_{a}} + D)],\quad {{\xi }_{3}} = 4{{R}_{1}}(2\gamma + \pi ) - 3\pi D$

В нижней части фиг. 4 изображены зависимости безразмерной нагрузки p₁ = = ${{P}_{1}}R_{1}^{2}{\text{/}}({{\sigma }_{0}}{{H}^{2}})$ от параметра вставки ${{d}_{a}}$, вычисленные по формуле (3.12) с учетом выражений (4.4).

Из фиг. 4 видно, что при одинаковом направлении армирования нагрузки ${{p}_{0}}$ и ${{p}_{1}}$ возрастают при расположении арматуры ближе к лицевым поверхностям пластины.

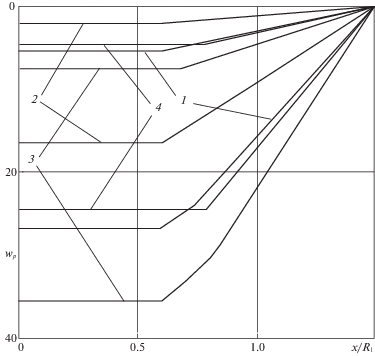
На фиг. 5 приведены безразмерные остаточные прогибы

$w = u({{t}_{f}})R_{1}^{2}{{\rho }_{0}}{\text{/}}({{\sigma }_{0}}{{H}^{2}}{{T}^{2}})$

в сечении $y = 0$ защемленной пластины с жесткой вставкой с параметром ${{d}_{a}} = 0.9$ под действием нагрузок с прямоугольной формой импульса

$P(t) = {{p}_{{\max }}}{{\sigma }_{0}}{{H}^{2}}{\text{/}}R_{1}^{2}\quad {\text{п р и }}\quad 0 \leqslant t \leqslant T,\quad P(t) = 0\quad {\text{п р и }}\quad t > T$

Фиг. 5

Кривые 1–4 соответствуют тем же значениям плотности армирования, что и на фиг. 4. Верхние кривые каждой пары относятся к расчетам при ${{p}_{{\max }}} = 22$, когда все пластины деформируются по схеме 1 для “средних нагрузок”, нижние – при ${{p}_{{\max }}} = 40$, когда для случаев 1–3 нагрузка будет “высокой”, а для случая 4 – “средней”.

Безразмерные время деформирования ${{t}_{f}}$ и максимальные остаточные прогибы защемленной четырехслойной армированной пластины с контуром, состоящим из двух полуокружностей и двух отрезков прямой, приведены в таблице 1. При “средних” нагрузках получено аналитически, что

${{t}_{f}} = {{p}_{{\max }}}T{\text{/}}{{p}_{0}}$

(см. выражение (2.17)), а при “высоких” нагрузках получено численно, что для рассматриваемых случаев последнее равенство также приближенно выполняется.

Таблица 1

Номер кривой	${{p}_{0}}$	${{p}_{1}}$	${{p}_{{\max }}} = 22$		${{p}_{{\max }}} = 40$
Номер кривой	${{p}_{0}}$	${{p}_{1}}$	${{t}_{f}}{\text{/}}T$	$\max w$	${{p}_{{\max }}}{\text{/}}{{p}_{0}}$	${{t}_{f}}{\text{/}}T$	$\max w$
1	12.24	26.09	1.80	5.51	3.27	3.24	22.72
2	17.09	36.38	1.29	2.00	2.35	2.34	16.54
3	10.21	27.55	2.15	7.49	3.92	3.99	35.61
4	12.38	42.71	1.78	4.69	3.23	3.23	24.49

Пластина с контуром в форме обобщенного суперэллипса. В качестве другого примера рассмотрим динамическое поведение армированной пластины с контуром в форме обобщенного суперэллипса (generalized super-ellipse) [28], заданным соотношениями (фиг. 6)

${{L}_{1}}{\text{:}}\quad x = a{{(\cos \varphi )}^{{2/3}}},\quad y = {{\gamma }_{1}}a\sin \varphi ,\quad {{\gamma }_{1}} \leqslant 1,\quad 0 \leqslant \varphi < 2\pi $

Фиг. 6

Введем обозначения

$c = \cos {{\nu }_{2}},\quad s = \sin {{\nu }_{2}},\quad \tilde {B} = \sqrt {4{{s}^{2}} + 9\gamma _{1}^{2}{{c}^{{8/3}}}} $

Соотношения (1.1) для координат ($x,y$) и (${{\nu }_{1}},{{\nu }_{2}}$) принимают вид

$x = ac[{{c}^{{ - 1/3}}} + 3{{\nu }_{1}}{{\gamma }_{1}}{{c}^{{1/3}}}{{(a\tilde {B})}^{{ - 1}}}],\quad y = as[{{\gamma }_{1}} - 2{{\nu }_{1}}{{(a\tilde {B})}^{{ - 1}}}]$

$B({{\nu }_{2}}) = \frac{1}{3}a\tilde {B}{{c}^{{1/3}}},\quad R({{\nu }_{2}}) = \frac{{a{{{\tilde {B}}}^{3}}}}{{6{{\gamma }_{1}}(3 + {{s}^{2}})}}{{c}^{{ - 2/3}}}$

Тогда для выражения (1.3) получим

${{D}_{c}}({{\nu }_{2}}) = \frac{1}{2}a{{\gamma }_{1}}\tilde {B}$

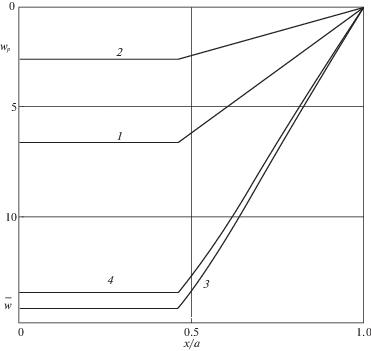
Рассмотрим четырехслойную пластину при ${{\gamma }_{1}} = 0.6$ с параметрами армирования такими же, как и в первом примере, при условии одинакового расхода арматуры (4.3). На фиг. 7 приведены зависимости безразмерной предельной нагрузки p₀ = = ${{P}_{0}}{{a}^{2}}{\text{/}}({{\sigma }_{0}}{{H}^{2}})$ и нагрузки ${{p}_{1}} = {{P}_{1}}{{a}^{2}}{\text{/}}({{\sigma }_{0}}{{H}^{2}})$ от параметра вставки ${{d}_{a}} = {{D}_{a}}{\text{/}}a \leqslant 0.54$. Кривые 1–5 соответствуют тем же значениям плотности армирования, что и на фиг. 4. Сплошные кривые относятся к шарнирному опиранию контура, штриховые – к его защемлению. В нижней части фиг. 7 кривая 5 практически совпадает с кривой 3. Для рассматриваемой пластины во всех случаях ${{d}_{0}} \equiv 0$, что может быть объяснено большим размером жесткой вставки.

Фиг. 7

На фиг. 8 приведены остаточные безразмерные прогибы

$w = u({{t}_{f}}){{a}^{2}}{{\rho }_{0}}{\text{/}}({{\sigma }_{0}}{{H}^{2}}{{T}^{2}})$

в сечении $y = 0$ защемленной пластины в форме обобщенного суперэллипса с жесткой вставкой (${{d}_{a}} = 0.54$) под действием нагрузки с линейно убывающей формой импульса

$P(t) = 60(1 - t{\text{/}}T){{\sigma }_{0}}{{H}^{2}}{\text{/}}{{a}^{2}}\quad {\text{п р и }}\quad 0 \leqslant t \leqslant T,\quad P(t) = 0\quad {\text{п р и }}\quad t > T$

Фиг. 8

Кривые 1–4 соответствуют тем же случаям значений плотности армирования, что и на фиг. 4. Нагрузка для случаев 1, 3 и 4 будет “высокой”, а для случая 2 – “средней”. Для рассматриваемых случаев численно получено, что для времени окончания деформирования пластины приближенно выполняется равенство (2.17).

Из проведенных расчетов видно, что при одинаковом расходе арматуры для рассматриваемых видов армирования защемленная пластина наиболее прочная (относительно критериев на основе максимума предельной нагрузки и минимума остаточного прогиба) в случае расположения арматуры в направлениях, нормальных к внешнему контуру пластины, и в слоях, находящихся ближе к ее лицевым поверхностям (т.е. в случае 2), что согласуется с идеей создания конструкций типа сэндвич-панелей [29–32].

Таким образом, разработанная модель динамического изгиба армированных криволинейных пластин дает качественно верное представление о деформации конструкции и может быть использована для инженерных приложений. Количество параметров предложенной математической модели позволяет в широком диапазоне изменять схему армирования, объемное содержание армирующих волокон, а также толщину слоев, физические характеристики композита, криволинейный контур пластины.

Список литературы

Янковский А.П. Вязкопластическая динамика металлокомпозитных оболочек слоисто-волокнистой структуры при действии нагрузок взрывного типа. I. Постановка задачи и метод решения // Матем. методи фіз.-мех. поля. 2012. Т. 55. № 2. С. 119–130. doi 10.1007/s10958-013–1421-7
Янковский А.П. Применение явного по времени метода центральных разностей для численного моделирования динамического поведения упругопластических гибких армированных пластин // Вычисл. мех. сплошных сред. 2016. Т. 9. № 3. С. 279–297. doi 10.7242/1999-6691/2016.9.3.24
Попов О.Н., Малиновский А.П., Моисеенко М.О., Трепутнева Т.А. Состояние вопроса по расчету неоднородных элементов конструкций за пределом упругости // Вестник ТГАСУ. 2013. № 4. С. 127–142.
Абросимов Н.А., Елесин А.В., Новосельцева Н.А. Численный анализ влияния структуры армирования на динамическое поведение и предельную деформируемость композитных оболочек вращения // Мех. композ. матер. 2014. Т. 50. № 2. С. 313–326. doi 10.1007/s11029-014-9409-z
Qatu M.S., Sullivan R.W., Wang W. Recent research advances on the dynamic analysis of composite shells: 2000–2009 // Comp. Struct. 2010. V. 93. P. 14–31. doi 10.1016/j.compstruct.2010.05.014
Arora H., Linz P.D., Dear J.P. Damage and deformation in composite sandwich panels exposed to multiple and single explosive blasts // Int. J. Impact Eng. 2017. V. 104. P. 95–106. doi 10.1016/j.ijimpeng.2017.01.017
Jones N. Some recent developments in the dynamic inelastic behaviour of structures // Ships Offshore Struct. 2006. V. 1. № 1. P. 37–44. doi 10.1533/saos.2005.0007
Hampson P.R., Moatamedi M. Review of composite structures subjected to dynamic loading // Int. J. Crashworthiness. 2007. V. 12. № 4. P. 411–428. doi 10.1080/13588260701483334
Немировский Ю.В., Романова Т.П. Динамическое сопротивление плоских пластических преград. Новосибирск: ГЕО, 2009. 311 с.
Немировский Ю.В. Об условии пластичности (прочности) для армированного слоя // ПМТФ. 1969. № 5. С. 81–88. doi 10.1007/BF00907434
Nemirovsky Ju.V., Resnikoff B.S. On limit equilibrium of reinforced slabs and effectiveness of their reinforcement // Arch. Inst. Inżynierii Lądowej. 1975. T. XXI. № 1. P. 57–67.
Kelly A., Tyson W.R. Tensile properties of fiber-reinforced metals: copper/tungsten and copper/molybdenum // J. Mech. Phys. Solids. 1965. V. 13. № 6. P. 329–350. doi 10.1016/0022-5096(65)90035-9
Сарбаев Б.С. Анализ несущей способности слоистых волокнистых композиционных материалов // Вестник МГТУ. Сер. Машиностр. 2000. № 4. С. 59–72.
Сарбаев Б.С. Расчет нижней границы предельной нагрузки для многослойных волокнистых композитов при двухосном нагружении // Инж. ж.: наука инновации. 2013. Вып. 7. С. 856–1–13. URL: http://engjournal.ru/catalog/machin/rocket/856.html
Ржаницын А.Р. Предельное равновесие пластинок и оболочек. М.: Наука, 1983. 288 с.
Абросимов Н.А., Баженов В.Г. Нелинейные задачи динамики композитных конструкций. Н. Новгород: Изд-во ННГУ, 2002. 391 с.
Немировский Ю.В., Романова Т.П. Динамика пластического деформирования пластин с криволинейным контуром // Прикл. мех. 2001. Т. 37. № 12. С. 68–78. doi 10.1023/A:1014841512071
Немировский Ю.В., Романова Т.П. Динамическая пластическая повреждаемость одно- и двусвязных эллиптических пластин // ПМТФ. 2002. Т. 43. № 2. С. 142–154. doi 10.1023/A:1014766028870
Немировский Ю.В., Романова Т.П. Динамическое поведение жесткопластических пластин в форме сектора // Прикл. механика. 2004. Т. 40. № 4. С. 93–101. doi 10.1023/B:INAM.0000034467.50580.ae
Romanova T.P., Nemirovsky Yu.V. Dynamic rigid-plastic deformation of arbitrarily shaped plates // J. Mech. Mater. Struct. 2008. V. 3. № 2. P. 313–334. doi 10.2140/jomms.2008.3.313
Немировский Ю.В., Романова Т.П. Динамическое деформирование криволинейной пластины с жесткой вставкой // ПМТФ. 2006. Т. 47. № 2. С. 126–138. doi 10.1007/s10808-006-0051-y
Немировский Ю.В., Романова Т.П. Динамика повреждаемости пластических армированных металлокомпозитных кольцевых пластин // Фундаментальные и прикладные проблемы современной механики: Сб. матер. конф. (Томск, 12–14 апреля 2011 г.). Томск: Томский гос. ун-т, 2011. С. 253–254.
Немировский Ю.В., Романова Т.П. Динамический изгиб армированных правильных полигональных пластин с жесткой шайбой под действием взрывных нагрузок // Сб. тр. Междунар. конф. “Актуальные проблемы прикладной математики, информатики и механики” (Воронеж, 20–22 сентября 2010 г.) Воронеж: Воронежский гос. ун-т, 2010. С. 255–269.
Романова Т.П. Моделирование динамического поведения мозаично-армированных трехслойных квадратных пластин // Пробл. прочн. пластичн. 2016. Вып. 78(2). С. 145–155.
Немировский Ю.В., Янковский А.П. Особенности вязкопластического деформирования армированных пластин переменной толщины при действии нагрузок взрывного типа // Прикл. мех. 2008. 44. № 2. С. 85–98. doi 10.1007/s10778-008-0030-5
Немировский Ю.В., Янковский А.П. Вязкопластическая динамика слоисто-волокнистых пластин переменной толщины при действии нагрузок взрывного типа // Мех. композ. матер. констр. 2006. Т. 12. № 4. С. 484–501.
Ерхов М.И. Теория идеально пластических тел и конструкций. М.: Наука, 1978. 352 с.
Zhou D., Lo S.H., Cheung Y.K., Au F.T.K. 3-D vibration analysis of generalized super elliptical plates using Chebyshev–Ritz method // Int. J. Solids Struct. 2004. V. 41. P. 4697–4712. doi 10.1016/j.ijsolstr.2004.02.045
Carrera E., Brischetto S. A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates // Appl. Mech. Reviews. Trans ASME. 2009. V. 62. № 1. P. 010803–1–17. doi 10.1115/1.3013824
Панин В.Ф., Гладков Ю.А. Конструкции с заполнителем. М.: Машиностр., 1991. 272 с.
Rezaeifard M., Salami S.J., Dehkordi M.B., Sadighi M. A new nonlinear model for studying a sandwich panel with thin composite faces and elastic-plastic core // Thin-Walled Struct. 2016. V. 107. P. 119–137. doi 10.1016/j.tws.2016.06.012
Fatt M.S.H., Palla L. Analytical modeling of composite sandwich panels under blast loads // J. Sandwich Struct. Mater. 2009. V. 11. № 4. P. 357–380. doi 10.1177/1099636209104515

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал